Уравнение плоскости проходящей через две прямые онлайн

Уравнение плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через три точки, и уравнение плоскости, проходящей через одну точку и имеющий заданный нормаль плоскости. Дается подробное решение с пояснениями. Для построения уравнения плоскости выберите вариант задания исходных данных, введите координаты точек в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение плоскости, проходящей через три точки

Рассмотрим цель − вывести уравнение плоскости, проходящей через три различные точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃), не лежащие на одной прямой. Так как эти точки не лежат на одной прямой, векторы и не коллинеарны. Следовательно точка M(x, y, z) лежит в одной плоскости с точками M₁, M₂, M₃ тогда и тольно тогда, когда векторы M₁M₂, M₁M₃ и компланарны. Но векторы M₁M₂, M₁M₃, M₁M компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Используя смешанное произведение векторов M₁M₂, M₁M₃, M₁M в координатах, получим необходимое и достаточное условие принадлежности точки M(x, y, z) к указанной плоскости:

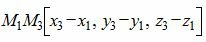
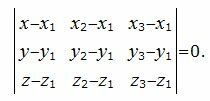Разложив определитель в левой части выражения, например, по первому столбцу и упростив, получим уравнение плоскости в общей форме, проходящий по точкам M₁, M₂, M₃:

Пример 1. Построить уравнение плоскости, проходящую через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2).

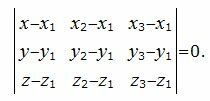(1)

Подставляя координаты точек A, B, C в (1), получим:

Разложим определитель по первому столбцу:

Уравнение плоскости, проходящей через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2) имеет вид:

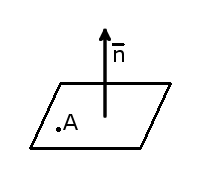
Уравнение плоскости, проходящей через одну точку и имеющий нормаль n

Пример 2. Построить плоскость, проходящую через точку M₀(-1, 2, 1) и имеюший нормаль n(1, 4/5, 1).

(2)

Подставляя координаты векторов M₀ и n в (2), получим:

Онлайн калькулятор. Уравнение плоскости

Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.

Найти уравнение плоскости

Выберите метод решения исходя из имеющихся в задаче данных:

В задаче известны:

Ввод данных в калькулятор для составления уравнения плоскости

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления уравнения плоскости

• Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Уравнение плоскости.

Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки

В зависимости от условий задачи уравнение плоскости можно составить следующими способами:

Если заданы координаты трех точек A( x ₁, y ₁, z ₁), B( x ₂, y ₂, z ₂) и C( x ₃, y ₃, z ₃), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле

Если заданы координаты точки A( x ₁, y ₁, z ₁) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Составление уравнения плоскости

Данный онлайн-сервис поможет составить уравнение плоскости по трем координатам.

Между всеми плоскостями и линейными уравнениями первого порядка с координатами (x,y,z) существуют взаимно-однозначные соответствия: каждая плоскость описывается определённым уравнением и наоборот, каждое уравнение описывает плоскость, притом только одну.

Координаты трех точек, не лежащих на одной прямой:

$$ (x_1, \: y_1, \: z_1) \quad (x_2, \: y_2, \: z_2) \quad (x_3, \: y_3, \: z_3)$$

Изображение плоскости, построенной по трем заданным точкам:

Составим систему уравнений для плоскости, проходящей через три заданные точки:

$$ \begin A \cdot (x-x_1)+B \cdot (y-y_1)+C \cdot (z-z_1)=0 \\ A \cdot (x-x_2)+B \cdot (y-y_2)+C \cdot (z-z_2)=0 \\ A \cdot (x-x_3)+B \cdot (y-y_3)+C \cdot (z-z_3)=0 \end $$

В этой системе произвольная точка (x, y, z) удовлетворяет уравнению плоскости.
Определитель этой системы равен нулю:

$$ \begin x-x_1 & x-x_2 & x-x_3 \\ y-y_1 & y-y_2 & y-y_3 \\ z-z_1 & z-z_2 & z-z_3 \end = 0$$

1. Дано три точки с координатами M(1;-2;0), K(2;0;-1), N(0;-1;2). Составьте уравнение плоскости, проходящей через эти точки.
   Посмотреть решение

Общий вид уравнения плоскости A·x+B·y+C·z+D=0, чтобы его составить, необходимо найти коэффициенты A, B, C, D.

Составим определитель, который поможет их найти:
$$ \begin x-x1 && x-x2 && x-x3 \\ y-y1 && y-y2 && y-y3 \\ z-z1 && z-z2 && z-z3 \end = 0 $$

Учитывая, что x1, x2, x3, y1, y2, y3, z1, z2, z3 – координаты точек M, K, N, подставим:

$$ \begin x-1 && x-2 && x-0 \\ y+2 && y-0 && y+1 \\ z-0 && z+1 && z-2 \end = 0$$

Решая определитель, получим: 5x-y+3z+7=0.

Ответ:

Поместим призму в систему координат таким образом, чтобы ее начало находилось в точке А1. Тогда координаты точек, определяющих положение плоскости в пространстве, будут:

Составим определитель, позволяющий найти уравнение плоскости:

$$ \begin x-0 && x-12 && x-0 \\ y-12 && y-0 && y-13 \\ z-0 && z-0 && z-8 \end = 0$$

Расчет определителя дает результат:

$$ 5x+13y+12z-156=0 $$ — это и есть уравнение плоскости.