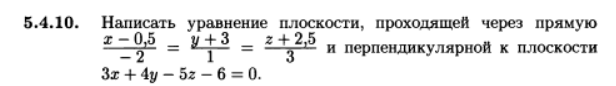Задача 53930 уравнение плоскости проходящей через.
Условие
уравнение плоскости проходящей через прямую и перпендикулярна к плоскости
Решение
Каноническое уравнение плоскости
Ax+By+Cz+D=0
⇒ координаты нормального вектора плоскости vector
Значит из уравнения плоскости
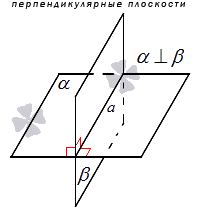
3x+4y-5z-6=0
получаем vector
vector=(-2;1;3) — направляющий вектор прямой
P(0,5; -3;-2,5) — точка, лежащая на прямой и стало быть на искомой плоскости
Пусть М (x;y;z) — произвольная точка плоскости.
Условием компланарности трех векторов является равенство нулю определителя третьего порядка,
составленного из координат этих векторов
Раскрываем определитель:
5*(x-0,5)+9(y+2)-8*(z+2,5)-3*(z+2,5)-12(x-0,5)+10(y+2)=0
Уравнение плоскости, проходящей через прямую перпендикулярно заданной плоскости онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через прямую L1 параллельно другой прямой L2 (прямые L1 и L2 не параллельны). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямых (канонический или параметрический) введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости проходящей через прямую перпендикулярно заданной плоскости − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L
 . . | (1) |
 . . | (2) |
Пусть плоскость α1 не перпендинулярно прямой L.
Задача заключается в построении уравнения плоскости α, проходящей через прямую L перпендикулярно плоскости α1 (Рис.1).
 |
Запишем уравнение искомой плоскости α:
| Ax+By+Cz+D=0. | (3) |
Искомая плоскость α проходит через прямую L, следовательно она проходит через точку M0(x0, y0, z0). Тогда справедливо следующее равенство:
| Ax0+By0+Cz0+D=0. | (4) |
и поскольку прямая L принадлежит этой плоскости, то нормальный вектор n=<A, B, C> и направляющий вектор q=<m, p, l> ортогональны:
Для того, чтобы плоскость α была перпендикулярна плоскости α1, нормальные векторы этих плоскостей должны быть ортогональными, т.е. скалярное произведение этих векторов должно быть равным нулю:
| AA1+BB1+CC1=0 | (6) |
Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (4)−(6). Представим систему линейных уравнений (4)−(6) в матричном виде:
 | (7) |
Решив однородную систему линейных уравнений (7) найдем частное решение. (Как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн). Подставляя полученные коэффициенты A, B, C и D в уравнение (3), получим уравнение плоскости, проходящей через прямую L перпендикулярно плоскости α1.
Пример 1. Найти уравнение плоскости α, проходящей через прямую L:
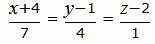 | (8) |
перпендикулярно плоскости α1 :
 | (9) |
Уравнение искомой плоскости α можно записать следующей формулой:
где n=<A, B, C> нормальный вектор плоскости.
Поскольку плоскость α проходит через прямую L , то она проходит также через точку M0(x0, y0, z0)=M0(−4, 1, 2), тогда уравнение плоскости должна удовлетворять условию:
| Ax0+By0+Cz0+D=0 | (10) |
а условие принадлежности прямой L к искомой плоскости α представляется следующим равенством:
| Am+Bp+Cl=0. | (11) |
Так как плоскость α должна быть перпендикулярна плоскости α1, то должна выполнятся условие:
| AA1+BB1+CC1=0 | (12) |
 | (13) |
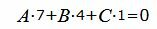 | (14) |
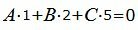 | (15) |
Представим эти уравнения в матричном виде:
 | (16) |
Решим систему линейных уравнений (16) отностительно A, B, C, D:
 | (17) |
Таким образом искомая плоскость имеет нормальный вектор n=<A, B, C>=<9/43,−17/43,5/43>. Тогда подставляя в уравнение плоскости
| Ax+By+Cz+D=0 | (18) |
значения A, B, C, D, получим:
 |
Уравнение плоскости можно представить более упрощенном виде, умножив на число 43:
 | (19) |
Ответ: Уравнение плоскости, проходящей через прямую (1) перпендикулярно плоскости (2) имеет вид (19).
Пример 2. Найти уравнение плоскости α, проходящей через прямую L:
 | (20) |
перпендикулярно плоскости α1 :
 | (21) |
Уравнение искомой плоскости α можно записать следующей формулой:
где n=<A, B, C> нормальный вектор плоскости.
Так как плоскость α проходит через прямую L , то она проходит также через точку M0(x0, y0, z0)=M0(−3, 1, 5), тогда уравнение плоскости должна удовлетворять условию:
| Ax0+By0+Cz0+D=0 | (22) |
а условие принадлежности прямой L к искомой плоскости α представляется следующим равенством:
| Am+Bp+Cl=0. | (23) |
Так как плоскость α должна быть перпендикулярна плоскости α1, то должна выполнятся условие:
| AA1+BB1+CC1=0 | (24) |
 | (25) |
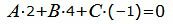 | (26) |
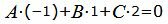 | (27) |
Представим эти уравнения в матричном виде:
 | (28) |
Решим систему линейных уравнений (28) отностительно A, B, C, D:
 | (29) |
Таким образом искомая плоскость имеет нормальный вектор n=<A, B, C>=<3/2,−1/2,1>. Тогда подставляя в уравнение плоскости
| Ax+By+Cz+D=0 | (30) |
значения A, B, C, D, получим:
 |
Уравнение плоскости можно представить более упрощенном виде, умножив на число 43:
 | (31) |
Ответ: Уравнение плоскости, проходящей через прямую (1) перпендикулярно плоскости (2) имеет вид (31).
Перпендикулярные плоскости, условие перпендикулярности плоскостей
Данная статья посвящена перпендикулярным плоскостям. Будут даны определения, обозначения вместе с примерами. Будет сформулирован признак перпендикулярности плоскостей и условие, при котором он выполним. Будут рассмотрены решения подобных задач на примерах.
Перпендикулярные плоскости – основные сведения
При наличии угла между пересекающимися прямыми можно говорить об определении перпендикулярных плоскостей.
При условии, что угол между перпендикулярными прямыми равен 90 градусов, их называют перпендикулярными.
Обозначение перпендикулярности принято писать знаком « ⊥ ». Если в условии дано, что плоскости α и β перпендикулярные, тогда запись принимает вид α ⊥ β . На рисунке ниже показано подробно.
Когда в улови дано, что плоскость α и β перпендикулярны, это значит, что α перпендикулярна β и наоборот. Такие плоскости называют взаимно перпендикулярными. Например, стена и потолок в комнате являются взаимно перпендикулярными, так как при пересечении дают прямой угол.
Перпендикулярность плоскостей – признак и условие перпендикулярности
На практике можно встретить задания, где необходимо определить перпендикулярность заданных плоскостей. Для начала нужно определить угол между ними. Если он равен 90 градусам, тогда они считаются перпендикулярными из определения.
Для доказательства перпендикулярности двух плоскостей применяют признак перпендикулярности двух плоскостей. Формулировка содержит понятия перпендикулярная прямая и плоскость. Напишем точное определение признака перпендикулярности в виде теоремы.
Если одна из двух заданных плоскостей пересекает прямую, перпендикулярную другой плоскости, то заданные плоскости перпендикулярны.
Доказательство имеется в учебнике по геометрии за 10 — 11 класс, где есть подробное описание. Из признака следует, что, если плоскость перпендикулярна линии пересечения двух заданных плоскостей, то она перпендикулярна к каждой из этих плоскостей.
Существует необходимое и достаточное условия для доказательства. Рассмотрим их для перпендикулярности двух заданных плоскостей, которое применяется в качестве проверки их перпендикулярности, находящихся в прямоугольной системе координат трехмерного пространства. Чтобы доказательство имело силу, необходимо применить определение нормального вектора плоскости, который способствует доказать необходимое и достаточное условие перпендикулярности плоскостей.
Для того, чтобы перпендикулярность пересекающихся плоскостей была явной, необходимо и достаточно, чтобы нормальные векторы заданных плоскостей пересекались под прямым углом.
Пусть в трехмерном пространстве задана прямоугольная система координат. Если имеем n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) , являющимися нормальными векторами заданных плоскостей α и β , то необходимым и достаточным условием перпендикулярности векторов n 1 → и n 2 → примет вид
n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0
Отсюда получаем, что n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) — нормальные векторы заданных плоскостей, а для действительности перпендикулярности α и β необходимо и достаточно, чтобы скалярное произведение векторов n 1 → и n 2 → было равным нулю, а значит, принимало вид n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0 .
Рассмотрим подробнее на примерах.
Определить перпендикулярность плоскостей, заданных в прямоугольной системе координат O x y z трехмерно пространства, заданного уравнениями x — 3 y — 4 = 0 и x 2 3 + y — 2 + z 4 5 = 1 ?
Для нахождения ответа на вопрос о перпендикулярности для начал необходимо найти координаты нормальных векторов заданных плоскостей, после чего можно будет выполнить проверку на перпендикулярность.
x — 3 y — 4 = 0 является общим уравнением плоскости, из которого можно сразу преобразовать координаты нормального вектора, равные n 1 → = ( 1 , — 3 , 0 ) .
Для определения координаты нормального вектора плоскости x 2 3 + y — 2 + z 4 5 = 1 перейдем от уравнения плоскости в отрезках к общему.
x 2 3 + y — 2 + z 4 5 ⇔ 3 2 x — 1 2 y + 5 4 z — 1 = 0
Тогда n 2 → = 3 2 , — 1 2 , 5 4 — это координаты нормального вектора плоскости x 2 3 + y — 2 + z 4 5 = 1 .
Перейдем к вычислению скалярного произведения векторов n 1 → = ( 1 , — 3 , 0 ) и n 2 → = 3 2 , — 1 2 , 5 4 .
Получим, что n 1 → , n 2 → = 1 · 3 2 + ( — 3 ) · — 1 2 + 0 · 5 4 = 3 .
Видим, что оно не равно нулю, значит, что заданные векторы не перпендикулярны. Отсюда следует, что плоскости также не перпендикулярны. Условие не выполнено.
Ответ: плоскости не перпендикулярны.
Прямоугольная система координат O x y z имеет четыре точки с координатами A — 15 4 , — 7 8 , 1 , B 17 8 , 5 16 , 0 , C 0 , 0 , 3 7 , D — 1 , 0 , 0 . Проверить, перпендикулярны ли плоскости А В С и A B D .
Для начала необходимо рассчитать скалярное произведение векторов данных плоскостей. Если оно равно нулю, только в этом случае можно считать, что они перпендикулярны. Находим координаты нормальных векторов n 1 → и n 2 → плоскостей А В С и A B D .
Из заданных координат точек вычислим координаты векторов A B → , A C → , A D → . Получаем, что:
A B → = 47 8 , 19 16 , — 1 , A C → = 15 4 , 7 8 , — 4 7 , A D → = 11 4 , 7 8 , — 1 .
Нормальный вектор плоскости А В С является векторным произведением векторов A B → и A C → , а для A B D векторное произведение A B → и A D → . Отсюда получим, что
n 1 → = A B → × A C → = i → j → k → 47 8 19 16 — 1 15 4 7 8 — 4 7 = 11 56 · i → — 11 28 · j → + 11 16 · k → ⇔ n 1 → = 11 56 , — 11 28 , 11 16 n 2 → = A B → × A D → = i → j → k → 47 8 19 16 — 1 11 4 7 8 — 1 = — 5 16 · i → + 25 8 · j → + 15 8 · k → ⇔ n 2 → = — 5 16 , 25 8 , 15 8
Приступим к нахождению скалярного произведения n 1 → = 11 56 , — 11 28 , 11 16 и n 2 → = — 5 16 , 25 8 , 15 8 .
Получим: n 1 → , n 2 → = 11 56 · — 5 16 + — 11 28 · 25 8 + 11 16 · 15 8 = 0 .
Если оно равно нулю, значит векторы плоскостей А В С и A B D перпендикулярны, тогда и сами плоскости перпендикулярны.
Ответ: плоскости перпендикулярны.
Можно было подойти к решению иначе и задействовать уравнения плоскостей А В С и A B D . После нахождения координат нормальных векторов данных плоскостей можно было бы проверить на выполнимость условие перпендикулярности нормальных векторов плоскостей.
http://matworld.ru/analytic-geometry/uravnenie-ploskosti6-online.php
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/perpendikuljarnye-ploskosti-uslovie-perpendikuljar/