Уравнение плоскости проходящей через три точки в отрезках

Глава 31. Уравнение плоскости, проходящей через три точки. Уравнение плоскости в отрезках

Уравнение плоскости, проходящей через три точки

Если точки M0(x0;y0;z0), M1(x1;y1;z1), M2(x2;y2;z2) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:

Написать уравнение плоскости, проходящей через три точки: M0(1;2;3), M1(2;1;2), M2(3;3;1).

Данные точки не лежат на одной прямой, так как векторы <1,–1,–1>и <2,1,–2>не коллинеарны. Плоскость M0M1M2 представляется уравнением т. е. x+z–4=0.

Уравнение плоскости в отрезках

А=D/A; B= D/B, C= D/A,

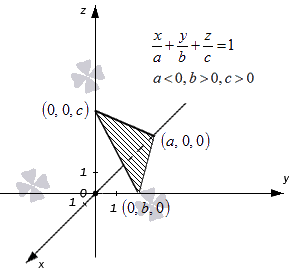
Называется Уравнением плоскости в отрезках, a, b и c –соответственно абсцисса, ордината и аппликата пересечения плоскости с осями Ox, Oy и Oz (рис. 2.17.1).

Написать уравнение плоскости 3x – 6y +2z – 12 = 0 в отрезках.

Очевидно, что a=4, b=–2, c=6. Тогда уравнение плоскости в отрезках есть

Уравнения плоскости, проходящей через три точки

Пусть в координатном пространстве заданы три точки не лежащие на одной прямой (рис.4.17). Требуется составить уравнение плоскости, проходящей через заданные точки.

Как было показано ранее (формула (1.23)), точка принадлежит плоскости, проходящей через точки тогда и только тогда, когда ее радиус-вектор удовлетворяет условию:

где — некоторые действительные числа (параметры). Это уравнение, а также его координатную форму

будем называть аффинным уравнением плоскости, проходящей через точки

в качестве направляющих векторов плоскости, составим уравнение вида (4.18):

которое называется уравнением плоскости, проходящей через три заданные точки .

Уравнение плоскости «в отрезках»

Пусть на координатных осях заданы точки и , причем (рис.4.18). Требуется составить уравнение плоскости, проходящей через эти три точки.

Подставляя в уравнение (4.21) координаты заданных точек , получаем:

Разделив уравнение на , получаем уравнение

которое называется уравнением плоскости «в отрезках» . Говорят, что плоскость, проходящая через точки и , отсекает на координатных осях «отрезки» : на оси абсцисс, на оси ординат и на оси аппликат. Разумеется, длины отрезков и равны и соответственно.

1. Перейти от общего уравнения плоскости (4.15) к уравнению «в отрезках» (4.22) можно при условии, что все коэффициенты общего уравнения отличны от нуля. Для этого нужно перенести свободный член в правую часть уравнения: , а затем разделить обе части уравнения на

Обозначив получим уравнение в отрезках (4.22):

2. Уравнения (4.21), (4.22), полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним, однако величины и в общем случае не равны длинам отсекаемых отрезков и .

Пример 4.9. В координатном пространстве (в прямоугольной системе координат) заданы точки

а) составить общее уравнение плоскости треугольника ;

б) составить уравнение в «отрезках» для плоскости треугольника ;

в) определить точки пересечения этой плоскости с координатными осями.

Решение. а) Составим уравнение (4.21):

Раскрывая определитель и приводя подобные члены, получаем

б) Переносим свободный член общего уравнения плоскости (см. пункт «а») в правую часть и делим уравнение на 12, получаем уравнение плоскости в «отрезках»:

в) По уравнению плоскости в «отрезках» заключаем, что плоскость (см. пункт «б») проходит через точки на координатных осях.

Уравнение плоскости в отрезках: описание, примеры, решение задач

Данный раздел будет полностью посвящен теме «Уравнение плоскости в отрезках». Мы последовательно рассмотрим, какой вид имеет уравнение плоскости в отрезках, применение этого уравнения для построения заданной плоскости в прямоугольной системе координат, переход от общего уравнения плоскости к уравнению плоскости в отрезках. В статье мы рассмотрим большое количество примеров, которые облегчат усвоение информации.

Уравнение плоскости в отрезках – описание и примеры

Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 , где a , b и c – это действительные числа, отличные от нуля. Абсолютные величины чисел a , b и c равны длинам отрезков, которые отсекаются плоскостью на осях координат O х , O у и O z в трехмерной системе координат O х у z . Откладываются длины отрезков от начала координат. Направление, в котором необходимо отложить длину отрезка, определяет знак, стоящий перед числом. Наличие «-» свидетельствует о том, что отрезок надо откладывать от нуля в отрицательном направлении оси.

Действительно, координаты точек a , 0 , 0 , 0 , b , 0 , 0 , 0 , c удовлетворяют уравнению плоскости в отрезках:

a a + 0 b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + b b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + 0 b + c c = 1 = 1 ⇔ 1 = 1

Поясним этот момент, расположив заданные точки на графике.

Проиллюстрируем описанное выше примером.

Плоскость проходит через точки — 2 , 0 , 0 , 0 , 3 , 0 и 0 , 0 , — 1 2 на осях координат в прямоугольной системе координат O x y z . Необходимо записать уравнение плоскости в отрезках.

Решение

Определим положение отрезков, отсекаемых плоскостью на осях координат. На оси абсцисс откладываем в отрицательном направлении отрезок длиной 2 единицы. На оси ординат в положительном направлении откладываем отрезок длиной 3 . На оси аппликат в отрицательном направлении откладываем отрезок длиной 1 2 .

При этом, уравнение плоскости в отрезках будет иметь вид: x — 2 + y 3 + z — 1 2 = 1 .

Ответ: x — 2 + y 3 + z — 1 2 = 1

Уравнение плоскости в отрезках удобно использовать для построения чертежей. Проиллюстрируем это утверждение примером.

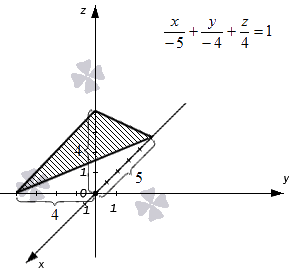
Плоскость в прямоугольной системе координат O х у z задана уравнением плоскости в отрезках вида x — 5 + y — 4 + z 4 = 1 . Необходимо изобразить эту плоскость на графике.

Решение

Изобразим оси координат, обозначаем начало координат и единичные отрезки на осях. Отмечаем длины отрезков, отсекаемых плоскостью, на каждой из осей. Соединяем концевые точки отрезков прямыми линиями. Полученная плоскость имеет вид треугольника. Она соответствует заданному уравнению плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .

Ответ:

Плоскость может быть задана уравнением плоскости другого вида. Для того, чтобы изобразить заданную плоскость на чертеже, можно сначала перейти к уравнению плоскости в отрезках. Получив уравнение плоскости в отрезках, нам останется лишь отметить точки a , 0 , 0 , 0 , b , 0 , 0 , 0 , c и соединить их прямыми линиями.

Приведение общего уравнения плоскости к уравнению плоскости в отрезках

Мы имеем общее уравнение плоскости в пространстве вида A x + B y + C z + D = 0 . И мы можем получить уравнение плоскости в отрезках. Сделать это можно в том случае, если плоскость пересекает все координатные оси, причем не в начале координат.

Не получится перевести общее уравнение плоскости в пространстве в уравнение плоскости в отрезках в тех случаях, когда плоскость проходит через одну из координатных осей или располагается параллельно оси. Другими словами, мы можем работать лишь с полным уравнением плоскости вида A x + B y + C z + D = 0 , где A ≠ 0 , B ≠ 0 , C ≠ 0 , D ≠ 0 .

Приведение общего уравнения плоскости к уравнению плоскости в пространстве производится следующим образом. Переносим слагаемое D в правую часть уравнения с противоположным знаком.

A x + B y + C z + D = 0 ⇔ A x + B y + C z = — D

Так как D ≠ 0 , то обе части полученного уравнения можно разделить на – D : A — D x + B — D y + C — D z = 1 .

Так как A ≠ 0 , B ≠ 0 , C ≠ 0 , то мы можем отправить в знаменатели коэффициенты перед переменными x , y и z . Последнее уравнение эквивалентно равенству x — D A + y — D B + z — D C = 1 . При этом мы использовали очевидное равенство p q = 1 q p , p , q ∈ R , p ≠ 0 , q ≠ 0 .

В итоге, мы получаем уравнение плоскости в отрезках. Это становится хорошо видно в том случае, если обозначить — D A = a , — D B = b , — D C = c .

Разберем решение примера.

Плоскость в прямоугольной системе координат O x y z в пространстве задана уравнением вида 3 x + 9 y — 6 z — 6 = 0 . Переведем это уравнение в уравнение плоскости в отрезках.

Решение

Данное в условии задачи уравнение является полным уравнением плоскости. Это дает нам возможность привески его к уравнению плоскости в отрезках. Перенесем — 6 в правую часть равенства, а затем разделим обе части равенства на 6 :

3 x + 9 y — 6 z — 6 = 0 ⇔ 3 x + 9 y + 6 z = 6 3 x + 9 y — 6 z = 6 ⇔ 1 2 x + 3 2 y — z = 1

Коэффициенты при переменных x, y и z отправим в знаменатели: 1 2 x + 3 2 y — z = 1 ⇔ x 2 + y 2 3 + z — 1 = 1 . Полученное уравнение и есть уравнение плоскости в отрезках.

Ответ: x 2 + y 2 3 + z — 1 = 1