Уравнение плоскости способы их задания

Плоскость

Способы задания плоскости

Общее уравнение плоскости (рис. 4.13)

где — нормальный вектор плоскости.

В векторном виде .

Частные случаи общего уравнения плоскости:

1) By + Cz + D = 0 — параллельна оси Ox;

2) Ax + Cz + D = 0 — параллельна оси Oy;

3) Ax + By + D = 0 — параллельна оси Oz;

4) Cz + D = 0 — параллельна оси Oxy;

5) By + D = 0 — параллельна оси Oxz;

6) Ax + D = 0 — параллельна оси Oyz;

7) Ax + By + Cz = 0 — проходит через начало координат;

8) By + Cz = 0 — проходит через ось Ox;

9) Ax + Cz = 0 — проходит через ось Oy;

10) Ax + By = 0 — проходит через ось Oz;

Уравнение плоскости, виды уравнения плоскости

В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.

Определение уравнения плоскости

Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.

Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.

Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.

Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.

Общее уравнение плоскости

Сформулируем теорему, а затем запишем уравнение плоскости.

Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве

Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.

Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.

Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.

Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .

Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.

Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.

Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .

Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.

Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.

Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.

Нормальное уравнение плоскости

Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .

Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.

n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1

То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.

Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.

Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.

Уравнение плоскости в отрезках

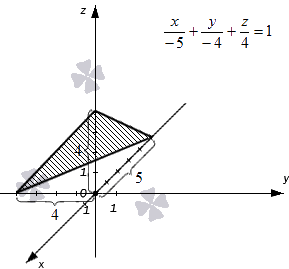
Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.

Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .

Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.

Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .

Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.

Типовые задачи с плоскостями

Составление уравнений плоскостей

Разнообразие видов уравнений плоскостей порождается многообразием геометрических способов их задания. По любому набору геометрических данных, однозначно определяющих плоскость, можно составить уравнение этой плоскости, причем геометрические данные будут отражены в коэффициентах уравнения. И наоборот, коэффициенты любого уравнения плоскости имеют геометрический смысл, соответствующий способу задания плоскости.

Для удобства решения типовых задач, связанных с плоскостями, все основные типы уравнений плоскостей и соответствующие геометрические способы задания этих плоскостей отражены в таблице 4.1.

Примеры составления плоскостей по геометрическим данным указанны в таблице 4.1.

Таблица 4.1. Основные типы уравнений плоскостей

Метрические приложения уравнений плоскостей

Перечислим формулы для вычисления длин отрезков (расстояний) и величин углов по уравнениям образующих их плоскостей.

1. Расстояние от точки до плоскости вычисляется по формуле:

2. Расстояние между параллельными плоскостями и находится как расстояние от точки , координаты которой удовлетворяют уравнению до плоскости пo формуле:

3. а) Угол между двумя плоскостями и находится по формуле:

где и — нормали к плоскостям и соответственно.

находится величина того двугранного угла, образованного плоскостями и в котором лежат точки, принадлежащие разноименным полупространствам, определяемым данными плоскостями.

При решении задач свойства 1-3 используются наряду с метрическими приложениями векторной алгебры.

Пример 4.12. В координатном пространстве заданы вершины треугольной пирамиды Требуется:

а) составить общее уравнение плоскости, содержащей грань ;

б) найти расстояние от вершины до плоскости грани ;

в) найти величину угла между плоскостями граней и ;

г) найти величину двугранного угла, образованного гранями и пирамиды.

Решение. а) По формуле (4.21) составим уравнение плоскости проходящей через три точки

Разлагая определитель по первой строке, получаем

Итак, искомое уравнение составлено.

б) Для нахождения расстояния составим уравнение плоскости, проходящей через точки (см. пункт «а»):

Расстояние находим по формуле пункта 1 (см. метрические приложения) для

в) Острый угол между плоскостями и находим по формуле пункта 3,»а»:

г) Двугранный угол , образованный гранями и пирамиды либо равен острому углу между плоскостями граней, либо дополняет его до Вычисляя угол по формуле пункта 3,»б», получаем тот же результат, что и в пункте «в»: т.е. острому углу принадлежат точки, принадлежащие разноименным полупространствам. Выясним, в каких полупространствах (одноименных или разноименных) относительно плоскостей граней и лежит пирамида. Для этого достаточно проверить одну точку пирамиды, не принадлежащую граням и Возьмем точку — середину ребра (рис.4.23). Вычислим значения линейных четырехчленов в этой точке:

Следовательно, точка принадлежит одноименным полупространствам. Поэтому двугранный угол при ребре не острый, а тупой, т.е.

Системы линейных уравнений с тремя неизвестными

Системой линейных алгебраических уравнений с тремя неизвестными называется система уравнений вида

Числа называются коэффициентами системы; — свободными членами; — неизвестными.

Решением системы называется такая упорядоченная тройка чисел что после замены неизвестных соответственно числами каждое уравнение системы превращается в верное числовое равенство. На системы с тремя неизвестными переносятся все термины, применяемые к системам с двумя неизвестными.

Матричная запись неоднородной системы уравнений (4.29) имеет вид

где — матрица системы, — столбец свободных членов, – столбец неизвестных.

Рангом системы уравнений (4.29) называется ранг матрицы системы: т.е. максимальное число линейно независимых строк матрицы (максимальное число линейно независимых уравнений системы).

Рассматривается случай, когда все уравнения системы первой степени, т.е. коэффициенты при неизвестных каждого уравнения не равны нулю одновременно. Поэтому матрица системы ненулевая, более того, все ее строки ненулевые.

Поскольку матрица системы (4.29) ненулевая и содержит три столбца, то ее ранг Ранг может быть равен либо единице ( если все строки матрицы пропорциональны), либо двум ( если имеются две линейно независимые строки), либо трем ( , если имеются три линейно независимые строки).

Выясним геометрический смысл и свойства решений системы уравнений (4.29).

Пусть в пространстве задана аффинная система координат Множество точек координаты которых удовлетворяют линейному уравнению с тремя неизвестными

представляет собой плоскость. Поэтому множество решений системы уравнений является пересечением плоскостей

Рассмотрим примеры пересечения плоскостей .

1. Если ранг системы (4.29) равен 1, то коэффициенты при неизвестных всех уравнений пропорциональны. В этом случае любые две плоскости параллельны (система уравнений несовместна (рис.4.24,а)) или совпадают (в этом случае вся система (4.29) равносильна одному, например, первому ее уравнению (рис.4.24,б)).

2. Если ранг системы равен 2, то в системе имеются два линейно независимых уравнения. Плоскости, соответствующие этим уравнениям, пересекаются, например, по прямой (рис. 4.24,в,г). Поэтому множеством решений системы (4.29) является либо эта прямая (система совместна, все плоскости проходят через прямую т.е. все плоскости принадлежат собственному пучку плоскостей (рис. 4.24,в)), либо пустое множество (система несовместна (рис.4.24,г)).

3. Если ранг системы равен 3, то в системе имеются три линейно независимых уравнения. Плоскости, соответствующие этим уравнениям, пересекаются в одной точке, например, в точке (рис. 4.24,д,е). Поэтому множеством решений системы (4.29) является либо одна точка (система совместна, все плоскости проходят через точку т.е. все плоскости принадлежат собственной связке плоскостей (рис. 4.24,д)), либо пустое множество (система несовместна (рис. 4.24,е)).