Уравнение плоскости уравнение сферы презентация

Уравнения сферы, плоскости и прямой
презентация к уроку по геометрии (10, 11 класс)

Уравнения сферы, плоскости и прямой

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Понятие сферы и её элементов Уравнение сферы в заданной системе координат СФЕРА УРАВНЕНИЕ СФЕРЫ

Тело вращения — сфера

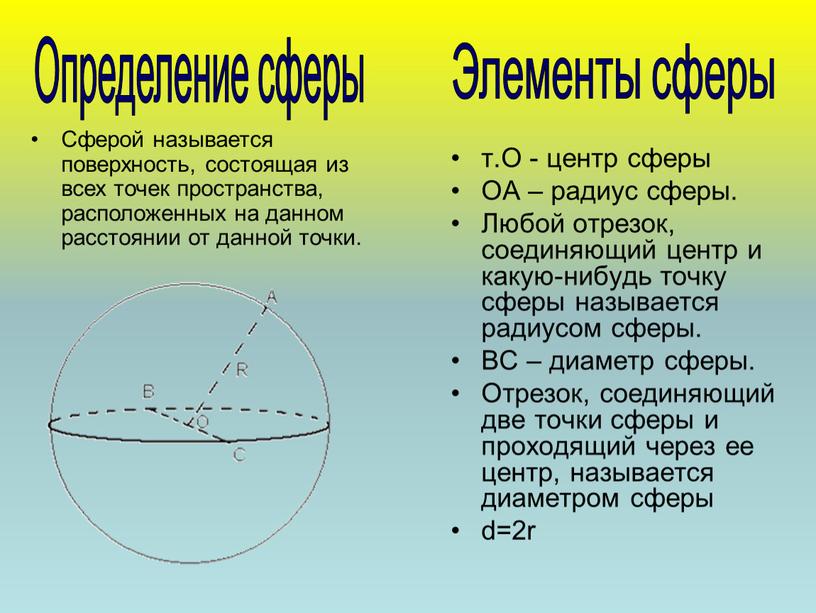
Определение сферы Элементы сферы Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. т.О — центр сферы ОА – радиус сферы. Любой отрезок, соединяющий центр и какую-нибудь точку сферы называется радиусом сферы. ВС – диаметр сферы. Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы d=2r

? Какие из тел, изображенных на рисунках, являются сферой? 1 2 3 4 5 6

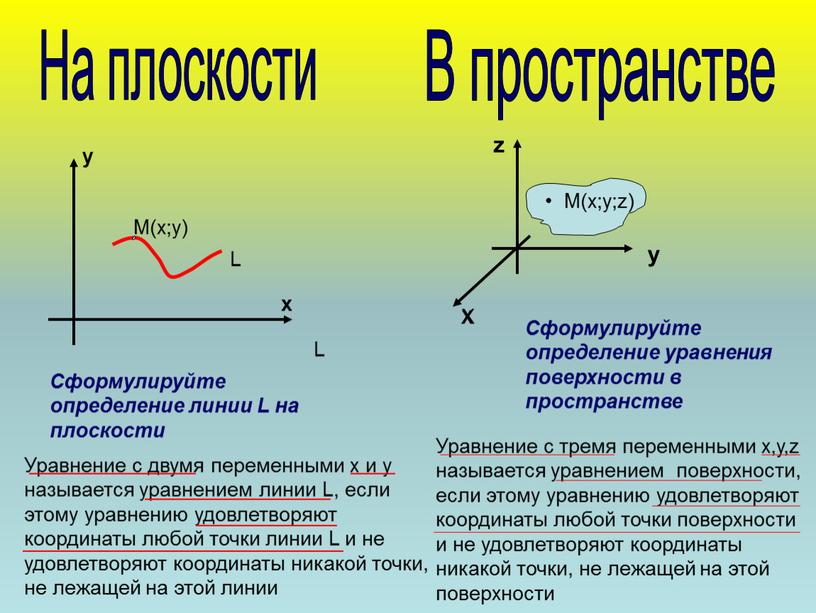
На плоскости В пространстве L М(х;у) х у L Сформулируйте определение линии L на плоскости Уравнение с двумя переменными х и у называется уравнением линии L , если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии Уравнение с тремя переменными х,у, z называется уравнением поверхности, если этому уравнению удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности Х z Сформулируйте определение уравнения поверхности в пространстве Х у М(х;у; z ) •

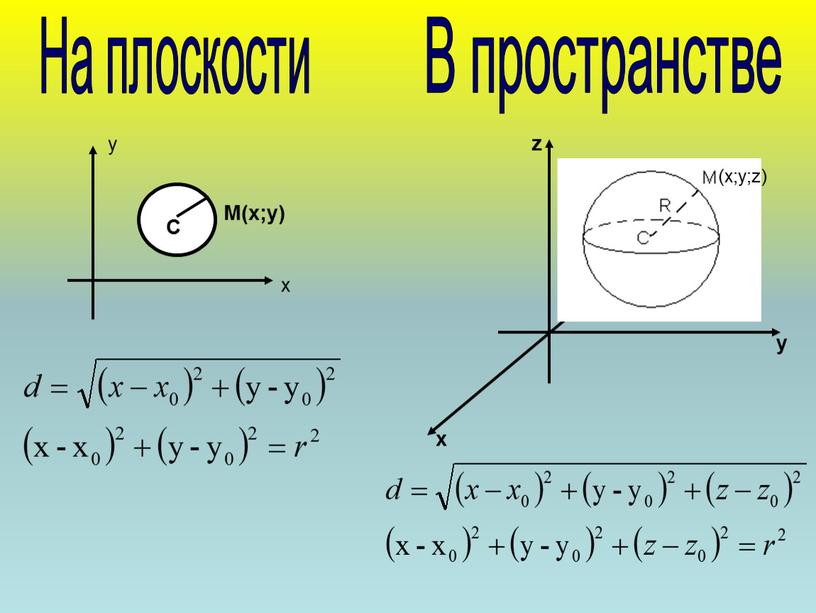
На плоскости В пространстве М(х;у) х у х у z (х;у; z ) С

Частные случаи 1.Уравнение окружности с центром в т.О(0;0) и радиусом r 1.Уравнение сферы с центром в т.О(0;0;0) и радиусом R

Выбрать из предложенных уравнений – уравнение сферы: 1. 2. 3. 4. 5. 6. 7. 8. 1.Ур-е окружности 2.Ур-е сферы 3.Ур-е прямой 4.Ур-е сферы 5.Ур-е параболы 6.Ур-е сферы 7.Ур-е сферы 8. ?

В данных уравнениях определите координаты центра сферы и радиус 1. 2. 3. 4.

Составьте уравнение сферы по следующим данным центра и радиуса сферы: Дано: С(-2;8;1); R =11 Дано: А(3;-2;0); R =0,7 Дано: О(0;0;0); R =1 Проверяем ответы:

Задача Определить принадлежит ли т.А сфере, заданной уравнением если: а) т.А(5;-2;6) б) т.А(-5;2;6) Решение: Равенство верное , следовательно А(5;-2;6) принадлежит сфере Равенство неверное , следовательно А(5;-2;6) не принадлежит сфере

Уравнение плоскости и прямой

совпадают, если существует такое число k , что параллельны, если существует такое число k , что В остальных случаях плоскости пересекаются.

Если известна какая-нибудь точка плоскости M 0 и какой-нибудь вектор нормали к ней , то через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору. Общее уравнение плоскости будет иметь вид: n (A;B;C) M 0

Чтобы получить уравнение плоскости , имеющее приведённый вид, возьмём на плоскости произвольную точку M( x ; y ; z ) . Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис), а для этого, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е. Вектор задан по условию. Координаты вектора найдём по формуле : Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме:

Используем формулу A ( x — x 0 )+B(y-y 0 )+C(z-z 0 )=0

Уравнение прямой в пространстве Поскольку прямую в пространстве можно рассматривать как линию пересечения двух плоскостей, то одним из способов аналитического задания прямой в пространстве является задание с помощью системы из двух уравнений задающих пару пересекающихся плоскостей.

Уравнение прямой в пространстве Прямую, проходящую через точку A 0 ( x 0 , y 0 , z 0 ) с направляющим вектором ( a , b , c ) можно задавать параметрическими уравнениями В случае, если прямая в пространстве задается двумя точками A 1 ( x 1 , y 1 , z 1 ), A 2 ( x 2 , y 2 , z 2 ), то, выбирая в качестве направляющего векто­ра вектор ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) и в качестве точки А 0 точку А 1 , получим следующие уравнения

Упражнение 1 Какими уравнениями задаются координатные прямые? Ответ: Ось Ox Ось O y Ось O z

Упражнение 2 Напишите параметрические уравнения прямой, проходящей через точку А (1,-2,3) с направляющим вектором, имеющим координаты (2,3,-1). Ответ:

Упражнение 3 Напишите параметрические уравнения прямой, проходящей через точки А 1 (-2,1,-3), А 2 (5,4,6). Ответ:

Упражнение 4 Напишите параметрические уравнения прямой, проходящей через точку M (1,2,-3) и перпендикулярную плоскости x + y + z + 1 = 0. Ответ:

Упражнение 5 В каком случае параметрические уравнения определяют перпендикулярные прямые? Ответ: Если выполняется равенство a 1 a 2 +b 1 b 2 +c 1 c 2 = 0 .

По теме: методические разработки, презентации и конспекты

Практическая работа «Построение углов между плоскостями, между прямой и плоскостью»

Практическая работа по геометрии ,10 класс. Хотя данную работу можно провести при подготовке к ЕГЭ по математике, при решении задач типа С2. Работа содержит 8 заданий на построение угла между прямой и.

Тест по теме «Параллельность прямых и плоскостей. Перпендикулярность прямых в пространстве» (геометрия 10 класс)

Данный тест можно предложить учащимся как входной перед изучением темы «Многогранники».

Параллельность прямых и плоскостей. Параллельные прямые в пространстве

Урок-презентация по геометрии 10 класс.

Тесты по теме «Прямые в пространстве. Параллельность прямых, прямой и плоскости», «Перпендикулярность прямых, прямой и плоскости»

Тесты предназначены для проверки усвоенияследующих понятий и определений: взаимное расположение прямых в пространстве, определение скрещивающихся прямых, определение параллельных прямых, признак парал.

Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространстве

Материал для практической работы «Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространств.

Расстояние от точки до плоскости, от прямой до плоскости

Материал для практической работы «Расстояние от точки до плоскости, от прямой до плоскости&quot.

Составление уравнений сферы, плоскости, прямой.

Составление уравнений сферы, плоскости, прямой.

Уравнение сферы, плоскости, прямой

Понятие сферы и её элементов Уравнение сферы в заданной системе координат

Понятие сферы и её элементов
Уравнение сферы в заданной системе координат

Тело вращения — сфера

Тело вращения — сфера

Определение сферы Элементы сферы

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

т.О — центр сферы
ОА – радиус сферы.
Любой отрезок, соединяющий центр и какую-нибудь точку сферы называется радиусом сферы.
ВС – диаметр сферы.
Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы
d=2r

На плоскости В пространстве Уравнение с двумя переменными х и у называется уравнением линии

Уравнение с двумя переменными х и у называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии

Уравнение с тремя переменными х,у,z называется уравнением поверхности, если этому уравнению удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности

На плоскости В пространстве М(х;у) х у х у z (х;у;z)

Уравнение плоскости и прямой

Уравнение плоскости и прямой

Общее уравнение плоскости Ax+By+Cz+D=0 где

Общее уравнение плоскости

где А, В, С, D – числовые коэффициенты

Особые случаи уравнения: D = 0 

Особые случаи уравнения:

D = 0  Ax+By+Cz = 0
плоскость проходит через начало координат.
А = 0  Ву + Cz +D = 0
плоскость параллельна оси Ох.
В = 0  Ах + Cz +D = 0
плоскость параллельна оси Оу.
C = 0  Ax+By+D = 0
плоскость параллельна оси Oz.

Особые случаи уравнения: А = В = 0 

Особые случаи уравнения:

А = В = 0  Сz + D = 0
плоскость параллельна плоскости Оху.
А = С = 0  Ву + D = 0
плоскость параллельна плоскости Охz.
В = C= 0  Ах+D = 0
плоскость параллельна плоскости Оуz.

Особые случаи уравнения: A = D = 0 

Особые случаи уравнения:

A = D = 0  By+Cz = 0
плоскость проходит через ось Ox.
B = D = 0  Ax + Cz = 0
плоскость параллельна оси Оy.
C = D = 0  Ах + By = 0
плоскость параллельна оси Оz.

Уравнения координатных плоскостей x = 0, плоскость

Уравнения координатных плоскостей

x = 0, плоскость Оyz
y = 0, плоскость Оxz
z = 0, плоскость Оxy

Две плоскости в пространстве: параллельны, если существует такое число k, что

совпадают, если существует такое число k, что

Две плоскости в пространстве:

параллельны, если существует такое число k, что

В остальных случаях плоскости пересекаются.

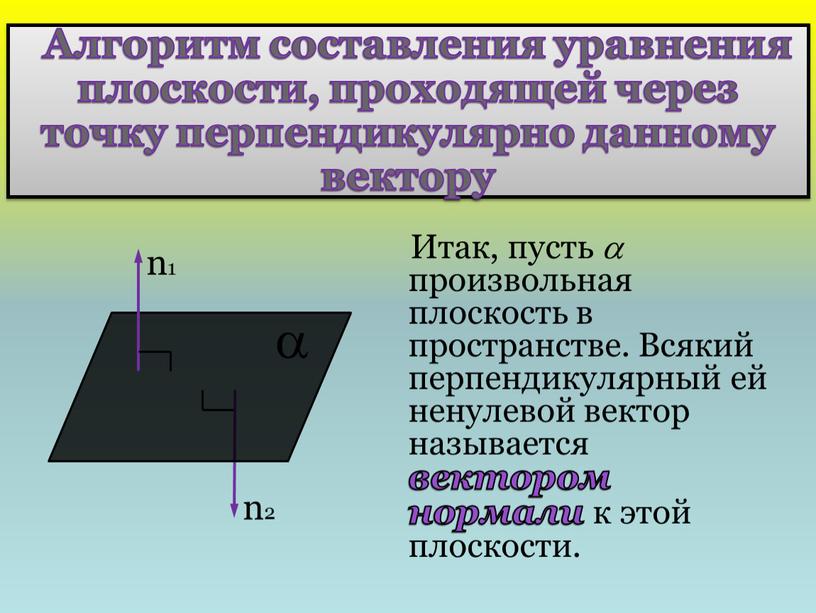
Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору

Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору

Итак, пусть  произвольная плоскость в пространстве. Всякий перпендикулярный ей ненулевой вектор называется вектором нормали к этой плоскости.

Если известна какая-нибудь точка плоскости

Если известна какая-нибудь точка плоскости M0 и какой-нибудь вектор нормали к ней, то через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору. Общее уравнение плоскости будет иметь вид:

Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору

Чтобы получить уравнение плоскости , имеющее приведённый вид, возьмём на плоскости произвольную точку

Чтобы получить уравнение плоскости, имеющее приведённый вид, возьмём на плоскости произвольную точку M(x;y;z). Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис), а для этого, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е.

Вектор задан по условию. Координаты вектора найдём по формуле :

Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме:

Пример 1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору

Пример 1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .

Используем формулу
A(x-x0)+B(y-y0)+C(z-z0)=0

Решение:

Ответ: 5x + y — 4z — 3=0

Уравнение прямой в пространстве

Уравнение прямой в пространстве

Поскольку прямую в пространстве можно рассматривать как линию пересечения двух плоскостей, то одним из способов аналитического задания прямой в пространстве является задание с помощью системы из двух уравнений задающих пару пересекающихся плоскостей.

Уравнение прямой в пространстве

Уравнение прямой в пространстве

Прямую, проходящую через точку A0(x0,y0,z0) с направляющим вектором (a,b,c) можно задавать параметрическими уравнениями

В случае, если прямая в пространстве задается двумя точками A1(x1,y1,z1), A2(x2,y2,z2), то, выбирая в качестве направляющего векто­ра вектор (x2-x1,y2-y1,z2-z1) и в качестве точки А0 точку А1, получим следующие уравнения

Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости. — презентация

Презентация была опубликована 8 лет назад пользователемЛиана Яхнова

Похожие презентации

Презентация на тему: » Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости.» — Транскрипт:

1 Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости.

2 Цели урока: Ввести понятие сферы, шара и их элементов Вывести уравнение сферы в заданной прямоугольной системе координат Рассмотреть возможные случаи взаимного расположения сферы и плоскости Формировать навык решения задач по теме

3 Окружность Окружность – множество точек плоскости, равноудаленных от данной точки Точка О – центр окружности ОА — радиус О А

4 Сфера Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки Точка О – центр сферы Данное расстояние – радиус сферы (обозначается R)

5 Сфера Отрезок, соединяющий две точки сферы и проходящий через ее центр – диаметр сферы (равен 2R) Сфера может быть получена вращением полуокружности (АСВ) вокруг ее диаметра (АВ) О

6 Шар Тело, ограниченное сферой, называется шаром Шаром радиуса R и с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек

7 Уравнение сферы Пусть R – радиус сферы С(х,у,z) – центр окружности Расстояние от произвольной точки М(х,у,z) до точки С найдем по формуле Если точка М лежит на данной сфере, МС = R, или Координаты точки М удовлетворяют уравнению

8 Решение задач 574(а) 576 (а) 577 (а) 578 (устно)

9 Взаимное расположение сферы и плоскости Обозначения R – радиус сферы d – расстояние от центра до плоскости α Плоскость Оху совпадает с плоскостью α, поэтому ее уравнение имеет вид z=0 Центр сферы С лежит на положительной полуоси Оz, т.е. имеет координаты С(0;0;d) Уравнение сферы

10 Взаимное расположение сферы и плоскости Если координаты произвольной точки М (х;у;z) удовлетворяют обоим уравнениям, то М лежит как в плоскости α, так и на сфере. Вопрос о взаимном расположении сводится к исследованию системы уравнений Подставив z = 0 во второе уравнение, получим

11 Взаимное расположение сферы и плоскости 1) d

12 Взаимное расположение сферы и плоскости 2) d = R

R» title=»Взаимное расположение сферы и плоскости 3) d > R» > 13 Взаимное расположение сферы и плоскости 3) d > R R»> R»> R» title=»Взаимное расположение сферы и плоскости 3) d > R»>

15 Домашнее задание п.64 – (в) 577 (в) 581