Уравнение плоскости в аффинных координатах

Аффинные координаты

Аффинная система координат на прямой, на плоскости, в пространстве

Пусть в пространстве фиксирована точка . Совокупность точки и базиса называется аффинной (декартовой) системой координат :

– аффинная система координат на прямой (рис.2.1,а) — это точка и ненулевой вектор на прямой (базис на прямой);

– аффинная система координат на плоскости (рис.2.1,6) — это точка и два неколпинеарных вектора , взятые в определенном порядке (базис на плоскости);

– аффинная система координат в пространстве (рис.2.1,в) — это точка и три некомпланарных вектора , взятые в определенном порядке (базис в пространстве).

Точка называется началом координат . Прямые, проходящие через начало координат в направлении базисных векторов, называются координатными осями: — ось абсцисс, — ось ординат, — ось аппликат . Плоскости, проходящие через две координатные оси, называются координатными плоскостями .

Аффинная система координат в пространстве (или на плоскости) называется правой, если ее базис является правым, и левой, если её базис — левый.

Координаты векторов и точек в аффинной системе координат

Координатами вектора в заданной системе координат называются, как и ранее, коэффициенты в разложении вектора по базису (см. разд.1.3.1; 1.3.2; 1.3.3).

Для любой точки в заданной аффинной системе координат можно рассмотреть вектор начало которого совпадает с началом координат, а конец — с точкой (рис.2.1,а,б,в). Этот вектор называется радиус-вектором точки .

Координатами точки в заданной системе координат называются координаты радиус-вектора этой точки относительно заданного базиса. В пространстве это координаты вектора в базисе , т.е. коэффициенты в разложении (рис.2.1,в). Координаты точки записывают в виде . Первая координата называется абсциссой , вторая – ординатой , третья – аппликатой . На плоскости и на прямой координаты записывают в виде и согласно разложениям (рис.2.1,6), (рис.2.1,а). Координаты точки , или, что то же самое, координаты ее радиус-вектора представляют в виде координатного столбца (матрицы-столбца):

Найдем координаты вектора с началом в точке и концом в точке . Рассмотрим треугольник (рис.2.2). Радиус-векторы и представляются в виде , . По правилу треугольника (см. разд. 1.1.2) вычитания векторов получаем , т.е. вектор имеет координаты . Этим доказано следующее правило: чтобы найти координаты вектора,нужно из координат его конца вычесть соответствующие координаты его начала . Это же правило справедливо для аффинных систем координат на плоскости и на прямой.

1. В заданной системе координат каждой точке можно поставить в соответствие её координаты, причем это соответствие взаимно однозначное:

В частности, разным точкам соответствуют разные наборы координат.

2. Если вектор с координатами отложить от точки , то конец вектора будет иметь координаты .

3. Координаты точки , которая делит отрезок в отношении , находятся по координатам его концов и :

В частности, координаты середины отрезка равны среднему арифметическому соответствующих координат концов отрезка :

Координаты точки которая «делит» площадь треугольника в отношении 0,\,\beta>0,\,\gamma>0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAKgAAAAVBAMAAAAgMbgsAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAAX1bEJvBQdDnITGx8wJf6wAAAnVJREFUOMvFVc9rE0EYfZNMNpp42BJ/BQkEokKwC6HYg5LAklLwIhQtpakIKSZGxMC2SEBpwBgLFRW0NpeKsAg99BCIB28GcrI9eKla8WD/F2fnxyYbsoWCYg6Z2f1m3rzvfW++Bf7Pj+h/ByfysD8P3307FD3z8ZCt9LFf4Et6xuU5qXdtTzTYKnT800qPl0ZHQkW67hLtIZHxROudwIYvaHAT84NypdyHdgaGetBsdC2Gfd5dtwv6bQhqwlSz4z3UBznkmwrIsGCoyBaQdsbagkrwJ8jvYX5PFWo7ieuOdNmy0IzkVei2hXpS8V++8I5ParfEiygDPZDH58smrjpbYy2pO9uXKALXXpzaCAjlpyRqdQC0dPGeKBpZqQiR+6D01UGDPhGOkMwMBroI+tyk+2fForHYqj0ESho4+V0pUdG9oNrsuWYgo5xnOcsd0D0E2Ja1CSVObNX0goYZTbcsW00v6Gdg5bQqRHSuI5m+QfwHA3nm+rpsCk1zEpQRIb6gTrVdPhEOmuPpJ5gmVVVqqfdA9TUTYTf9O7qs/i+37priE55bcoZuEu0er1VVYcpCdTPEsCMcNmHihLT6pwrh4xroPqakUUIzKkWLj3Hu09BrTL+PCYMoS2k9tBDnBB8lSVpYo7Yjj851ApswihJUZBSUxQe7bAUTdHd8Z/urML9yMH2ZLUFzbipJPSjMwmN+hNYLGVzZEw/HdFFf1R7G5icdW9MlEM7lpu7KH7zE/pa5TSOiJYUX+vfnw2V22qKYb+vea4poyjys/6WETX0amfA8yR6t49KGtOnoRibdceNojZpf3ZjlE52W4/1/8a2xR738AxcTjszkPv2OAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, находятся по координатам его вершин :

В частности, координаты точки пересечения медиан треугольника равны среднему арифметическому соответствующих координат вершин треугольника :

Эти формулы следуют из свойств 2,4 аффинных и выпуклых комбинаций (см. разд. 1.6.1). Они остаются справедливыми и на координатной плоскости, если аппликаты всех точек положить равными нулю. Например, координаты середины отрезка , или координаты точки пересечения медиан треугольника

Пример 2.1. В некоторой аффинной системе координат известны координаты вершин треугольной пирамиды (см. рис.2.3): Найти координаты (в той же системе координат):

а) точки пересечения медиан треугольника ;

б) точки , которая делит отрезок в отношении .

Решение. Учитывая пункт 3 замечаний 2.1, получаем:

47. Аффинная система координат на прямой, плоскости и в пространстве

В случае прямой базис состоит из одного ненулевого вектора V = (V) и система координат (О, V) изображена на рис. 4.1. В системе координат на прямой каждая точка A прямой имеет одну координату A(X), определяему разложением вектора По базису, = XV. Тогда A(0), E(1), где V = .

Систему координат на прямой можно задать еще следующими способами:

Двумя различными точками О и E данной прямой. Тогда одну из точек, например О, берем в качестве начала системы координат, а в качестве базисного вектора возьмем вектор V = (см. рис. 4.2).

Точкой О, единичным отрезком ОE и положительным направлением данной прямой, которое отмечается стрелкой.

2Аффинная система координат на плоскости. В случае плоскости базис состоит из двух неколлинеарных векторов плоскости, V = (V1, V2), и система координат (О, V1, V2) изображена на рис. 4.3. В системе координат на плоскости каждая точка A плоскости имеет две координаты A(X, Y), определяемые разложением вектора По базису, = XV1+ YV2. Тогда A(0, 0), E1(1, 0), E2(0, 1), где V1 = , V2 = . Координаты точки называются соответственно Абсциссой и Ординатой.

Систему координат на плоскости можно задать еще следующими способами:

Тремя точками О, E1, E2 плоскости, не лежащими на одной прямой. Тогда одну из точек, например О, берем в качестве начала системы координат, а в качестве базисного вектора возьмем векторы V1 = , V2 = .

Двумя пересекающимися числовыми осями ОX, ОY данной плоскости с общим началом О. Ось ОX называется Осью абсцисс, ось ОY — Осью ординат.

Аффинная система координат (О, V1, V2) называется Правой (Левой), если поворот от вектора к вектору по кратчайшему направлению совершается против часовой стрелки (по часовой стрелке). На рис. 4.3 и 4.4 представлены правые системы координат.

3. Аффинная система координат в пространстве. В случае пространства базис состоит из двух некомпланарных векторов пространства, V = (V1,V2, V3), и система координат (О, V1, V2, V3) изображена на рис. 4.5. В этой системе координат каждая точка A пространства имеет три координаты A(X,Y,Z), определяемые разложением вектора по базису, = XV1+ YV2 + ZV3. Тогда A(0, 0, 0), E1(1, 0, 0), E2(0, 1, 0), E3(0, 0, 1), где V1 = , V2 = , V3 = . Координаты точки называются соответственно Абсциссой, ординатой и Аппликатой.

Истему координат в пространстве можно задать еще следующими способами:

Четверкой точек О, E1, E2, E3 пространства, не лежащими на одной плоскости. Тогда одну из точек, например О, берем в качестве начала системы координат, а в качестве базисного вектора возьмем векторы V1 = , V2 = , V3 = .

Тремя числовыми осями ОX, ОY, ОZ, не лежащими в одной плоскости с общим началом О. Ось ОX называется Осью абсцисс, ось ОY — Осью ординат, ось ОZ — Осью аппликат.

Аффинная система координат (О, V1, V2, V3) называется Правой (Левой), если тройка векторов V1, V2, V3 правая (левая) На рис. 4.5 и 4.6 представлены правые системы координат, а на рис. 4.7 левая система координат.

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Общее уравнение плоскости: основные сведения

Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

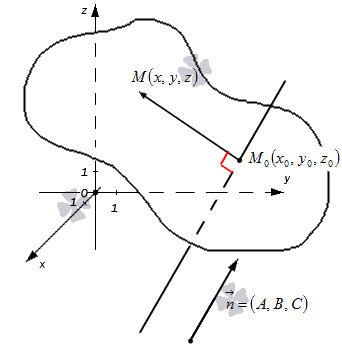
1. Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .

Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:

n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )

Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.

1. Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.

В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.

Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.

Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.

Раскроем чуть шире смысл теорем.

В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.

Укажем пример как иллюстрацию этих утверждений.

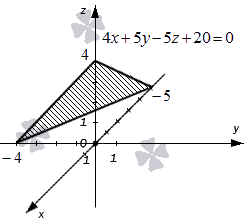
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

1. Исходные условия позволяют получить следующие данные:

x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0

1. Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0

Ответ: 3 x + 7 y — 5 z — 26 = 0

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

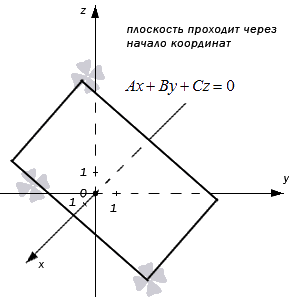
1. В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

1. Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.

1. При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0

Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.

Р​​ешение

У​​​​​словием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0

Ответ: x — 7 = 0

Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .

Решение

Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .

Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .