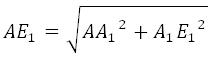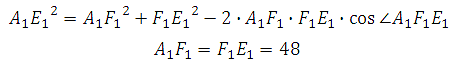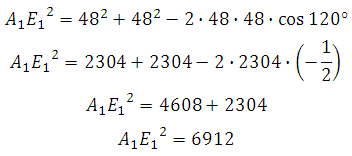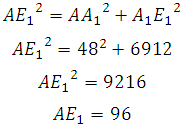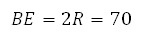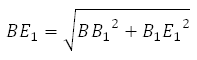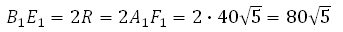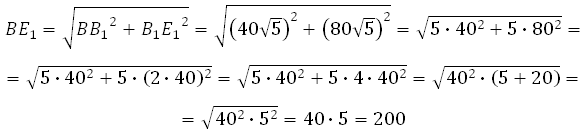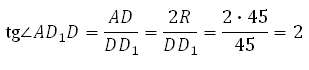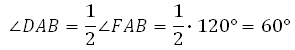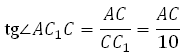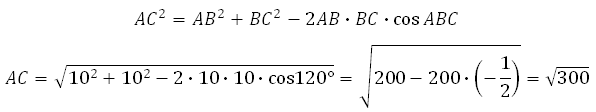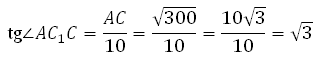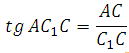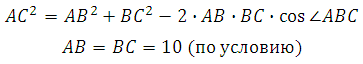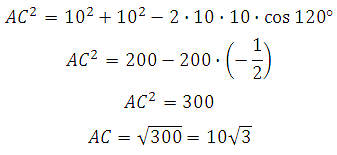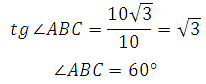Уравнение плоскости в правильной шестиугольной призме

Расстояние от точки до плоскости. Метод координат.

Нахождение расстояния от точки до плоскости методом координат (типовые задачи №14).

Просмотр содержимого документа
«Расстояние от точки до плоскости. Метод координат.»

Расстояние от точки до плоскости

Задачи на нахождение расстояния от точки до плоскости ( типовые задачи С2)

г. Железногорска Курской области

План проведения занятий.

• Нахождение расстояния от точки до плоскости по определению. Построение перпендикуляра к плоскости на основании признака перпендикулярности прямой и плоскости.
• Нахождение расстояния от точки до плоскости по определению. Построение перпендикуляра к плоскости на основании признака перпендикулярности прямой и плоскости.
• Нахождение расстояния от точки до плоскости. Построение перпендикуляра к плоскости на основании свойства перпендикулярных плоскостей.
• Нахождение расстояния от точки до плоскости. Построение перпендикуляра к плоскости на основании свойства параллельности прямой и плоскости.
• Нахождение расстояния от точки до плоскости методом объемов.

• Нахождение расстояния от точки до плоскости методом координат.

Метод координат – это один из самых универсальных методов геометрии. В принципе почти любую геометрическую задачу можно решить методом координат. Однако, попытки решать каждую задачу только координатным методом (имеются в виду, конечно, те задачи, в условии которых не говорится о координатах) часто приводят к тому, что даже простая геометрическая задача становится очень сложной алгебраической.

Главное при решении геометрических задач координатным методом – удачный выбор системы координат, т.е. выбор начала координат и направления осей. Обычно в качестве осей координат выбирают прямые, фигурирующие в условии задачи, или оси симметрии (если они есть) фигур, рассматриваемых в задаче. Желательно, чтобы выбранная система координат естественным образом определялась условием задачи.

Следует отметить, что при решении задачи координатным методом выпускник должен получить правильный ответ, и только тогда его решение будет оценено в 2 балла. В противном случае его решение не соответствует приведенным критериям и будет оценено в 0 баллов.

Метод координат можно использовать, вычисляя:

• расстояние между двумя точками;
• расстояние от точки до прямой;
• расстояние от точки до плоскости;
• угол между прямой и плоскостью;
• угол между плоскостями;
• расстояние между скрещивающимися прямыми.

Расположение относительно прямоугольной системы координат некоторых видов многогранников, наиболее часто используемых в задачах.

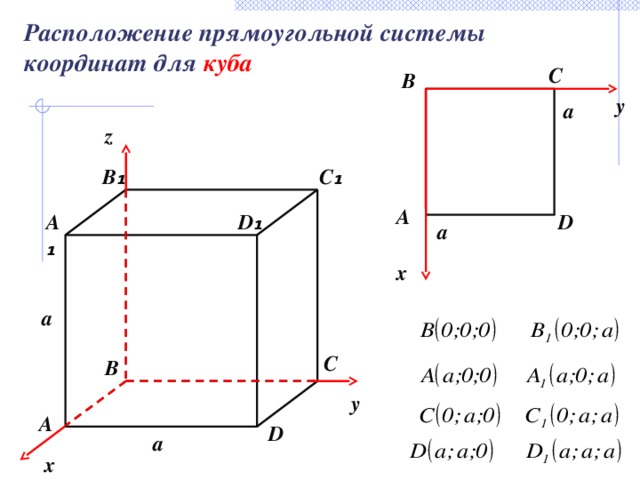
Расположение прямоугольной системы координат для куба

Метод координат в задачах типа С2.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

В ы б е р е м н а ч а л о к оо р д и н а т . П р о в е д е м т ри в з а и м н о п е р п е н д и к у л яр ны е о с и х , y и z . Выберем м а с ш т а б .

П о л у ч и л а с ь с и с т е м а к о о р д и н а т в т р е х м е р н о м п р о с т р а н с т в е .

К а ж д а я т о ч к а х а р а к т е р и з у е т с я т р е м я ч и с л а м и — к оо р д и н а т а м и п о x , y и z . З а п и с ь M ( − 1 ; 3 ; 2 ) о з н а ч а е т , ч т о к оо р д и н а т а т о ч к и M п о x ( а б с ц и сс а ) р а в н а − 1 , к оо р д и н а т а п о y ( о р д и н а т а ) р а в н а 3 , а к оо р д и н а т а п о z ( а пп л и к а т а ) р а в н а 2 .

В е к т о р ы в п р о с т р а н с т в е о п р е д е л яю т с я т а к ж е , к а к и н а п л о с к о с т и.

Э т о н а п р а в л е н ны е о т р е з к и, и м е ю щ и е н а ч а л о и к о н е ц . Т о л ь к о в п р о с т р а н с т в е в е к т о р з а д а е т с я т р е м я к оо р д и н а т а м и x , y и z :

ﺂ؟ ( x _a ; y _a ; z _a )

Чтобы н а й т и к о о р д и н а т ы в е к т о р а , так же, как и на плоскости, и з к оо р д и н а т ы к о н ц а надо в ы ч есть к оо р д и н а т у н а ч а ла.

1.

2.

Если точка M – середина отрезка AB , то ее координаты находятся по формуле:

3.

4. – сумма векторов.

5. – разность векторов.

6. – произведение вектора на число.

7. — скалярное произведение векторов

8. – косинус угла между векторами.

2. Введение системы координат.

Метод координат – это, конечно, очень хорошо, но в настоящих задачах C 2 никаких координат и векторов нет, поэтому их надо вводить.

Самое замечательное свойство заключается в том, что не имеет никакого значения как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.

2.1 Координаты куба.

Система координат вводится очень просто:

Начало координат – в точке A

Если ребро куба не указано, то принимаем его за единичный отрезок;

Ось x направляем по ребру АВ, у – по ребру А D , а ось z – по ребру AA _{1 .}

Теперь у каждой вершины куба есть координаты:

A (0; 0; 0), B (1; 0; 0), C (1; 1; 0), D (0; 1; 0),

2.2 Координаты правильной треугольной призмы

A (1; 0; 0), B , C (0; 0; 0), A ₁ (1; 0; 1), B ₁ , C ₁ (0; 0; 1).

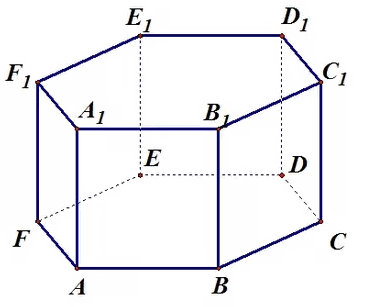
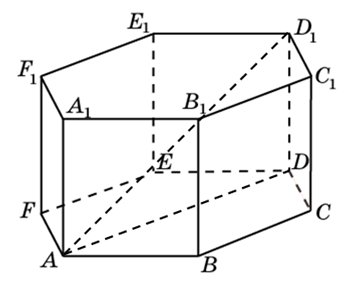
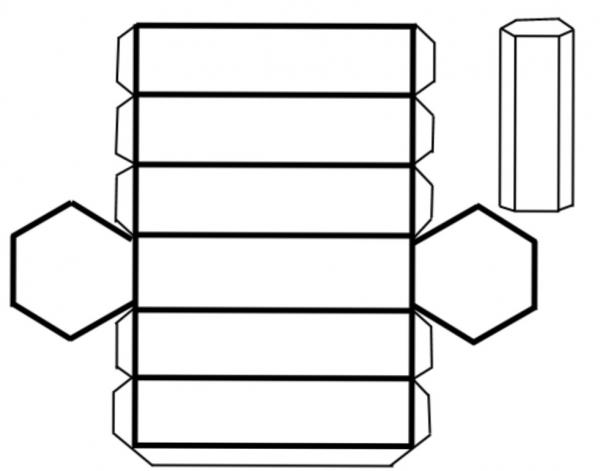
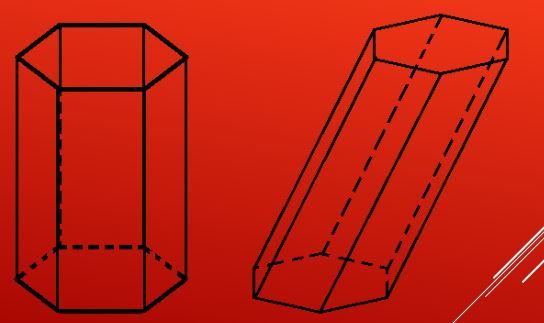
2.3 Координаты правильной шестиугольной призмы

2.4 Координаты правильной четырехугольной пирамиды

Введем систему координат с началом в точке А

Найдем координаты точки S . Рассмотрим треугольники ASH и ABH

AS = AB = 1 по условию;

Угол AHS = AHB = 90°, поскольку SH — высота, а AH ⊥ HB как диагонали квадрата;

Сторона AH — общая.

Следовательно, прямоугольные треугольники ASH и ABH равны по одному катету и гипотенузе. Значит, SH = BH = 0,5 · BD . Но BD — диагональ квадрата со стороной 1. Поэтому имеем:

Итак, координаты точки S :

Рассмотрим случай, если боковые ребра пирамиды не равны ребрам основания. В этом случае рассмотрим треугольник AHS :

Треугольник AHS — прямоугольный , причем гипотенуза AS — это одновременно и боковое ребро исходной пирамиды SABCD . Катет: AH = 0,5 · AC . Оставшийся катет SH найдем по теореме Пифагора . Это и будет координата z для точки S .

3. Матрицы и определители второго и третьего порядка.

Определение: Таблица, составленная из четырёх чисел называется квадратной матрицей второго порядка. Числа называют элементами матрицы.

Определение: Число ∆ называется определителем или детерминантом матрицы.

∆ =

Определитель третьего порядка можно вычислить так:

4. Метод координат в пространстве

4.1 Угол между прямыми.

Вычисление направляющих векторов для прямых.

В задаче С2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим направляющий вектор для прямой.

α -угол между прямыми

3.1 Угол между двумя прямыми – это угол между их направляющими векторами.

Задача 1 .

В единичном кубе ABCDA ₁ B ₁ C ₁ D ₁ найдите угол между прямыми AE и BF , где E – середина ребра A ₁ B ₁ , где Е – середина ребра А ₁ В ₁ а F – середина ребра B ₁ C _1.

Решение (1 способ)

K — середина A ₁ D ₁ AK ║ BF угол KAE = φ

По теореме Пифагора

По теореме косинусов для ∆ AKE

KE ² = AE ² + AK ² — 2 * AE * AK * cos φ

cos φ =0,8 φ = arccos 0.8

Решение (2 способ)

С помощью векторов и координат легко найти угол между прямыми.

А если требуется найти угол между плоскостями или между прямой и плоскостью, то для этого нам понадобится уравнение плоскости в пространстве.

4.2 Плоскость в пространстве задается уравнением.

Ax + By + Cz + D =0,

где A , B и С – координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; -2; 0) и К (4; 1; 2)

Уравнение плоскости выглядит так:

Ax + By + Cz + D =0

Получим систему из трех уравнений:

В ней четыре неизвестных: A , B , С и D . Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило – простое вместо одной из переменных можно взять любое число, не равное нулю.

Решив систему, получим:

A =- B =- C =

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на -3. Тогда коэффициенты станут целыми:

Вектор (1; 4; -7 ) – это нормаль к плоскости MNK .

Если плоскость проходит через начало координат, то D =0 (так как D ≠0 не позволит получить верное числовое равенство).

Уравнение плоскости, проходящей, через заданную точку имеет вид:

_{Уравнение плоскости можно составить и с помощью определителя третьего порядка :}

_{Пусть имеем точки}

_,

_{Тогда уравнение плоскости, проходящей через эти три точки ,будет иметь вид:}

₌₀

4.3 Угол между плоскостями равен углу между нормалями к этим плоскостям:

cos φ =

При пересечении двух плоскостей образуется четыре угла . Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения – чтобы косинус угла был неотрицателен.

В кубе A B C D A ₁ B ₁ C ₁ D ₁ то ч к и E и F с середины ребер соответственно A ₁ B ₁ и

A ₁ D ₁ . Найдите косинус у г л а между плоскостями A E F и B D D ₁ .

В и д н о , ч т о п л о с к о с т и A E F и B D D ₁ пересекаются где-то вне куба . В классическом решении пришлось бы строить пересечения . Н о координатный м е т о д з н а ч и т е л ь н о в с ё у п р о щ а е т . Достаточно о т м е т и ть к оо р д и н а т ы н у ж н ы х т о ч е к и н а й ти у г о л м е ж д у н о р м а л я м и к п л о с к о с т я м A E F и B D D ₁ .

A (0; 0; 0), C (1; 1; 0)

Сначала – нормаль к плоскости BDD ₁ . Мы можем подставить координаты точек B , D и D ₁ в уравнение плоскости и найти координаты вектора нормали. А можно увидеть нужную нормаль на чертеже. Ведь плоскость BDD ₁ – это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF .

A E F

_{Составим уравнение плоскости:}

Уравнение плоскости AEF : 2 x +2 y — z =0

Нормаль к плоскости AEF : (2; 2; -1)

Найдем угол между плоскостями:

_{4.4 Угол между прямой и плоскостью}

В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите угол между прямой DE , где E -середина апофемы SF грани ASB грани и плоскостью ASC

OB — вектор нормали плоскости ASC

DE — направляющий вектор прямой

OB — — вектор нормали плоскости ASC

DE — — вектор направляющей вектор прямой DE

Ответ:

4.5 Расстояние от точки до плоскости

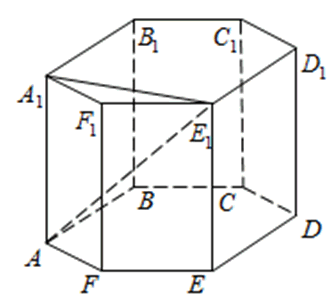
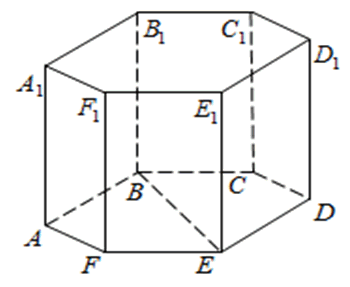
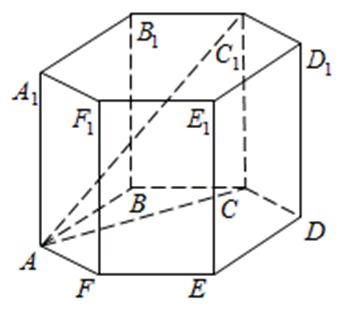
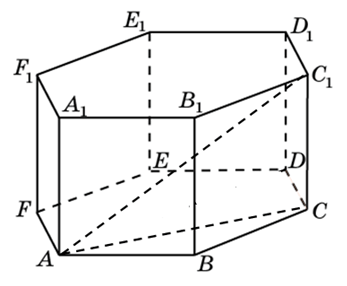
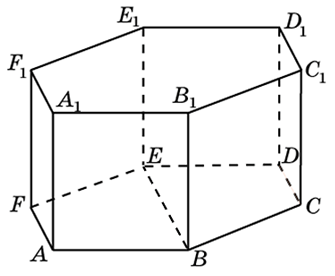
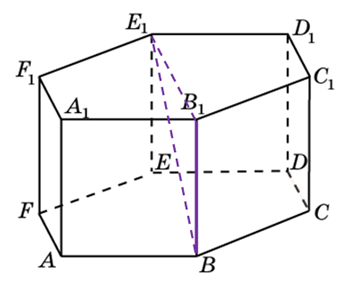
В правильной шестиугольной призме ABCDEFA ₁ B ₁ C ₁ D ₁ E ₁ F ₁ , все рёбра которой равны 1, найдите расстояние от точки E до прямой B ₁ C ₁ .

Решение (1 способ)

1) Рассмотрим Δ CDE :

по теореме косинусов:

СЕ 2 = 2 С D 2 — 2CD 2 cos120° = 2 + 2*1/2 = 3 =>

CE =

2) Рассмотрим ΔС ₁ СЕ: он прямоугольный, т.к. С ₁ С перпендикулярна плоскости нижнего основания => CC ₁ перпендикулярна СЕ.

По теореме Пифагора:

С ₁ Е 2 = ( ) 2 + 1 2 = 4, С ₁ Е = 2

3) Рассмотрим ΔBCE : он прямоугольный , т.к. 120° — 60°:2 = 90° (из Δ CDE )

ВЕ 2 = ( ) 2 + 1 2 = 4, ВЕ = 2

4) Рассмотрим ΔВВ ₁ Е: он прямоугольный, т.к. ВВ ₁ перпендикулярна ВЕ,

по теореме Пифагора:

В ₁ Е 2 = В ₁ В 2 + ВЕ 2 = 4 + 1 = 5, ВЕ =

С ₁ Е = 2, С ₁ В ₁ = 1, В ₁ Е = , т.е. 2 2 + 1 2 = ( ) 2 . Таким образом, по теореме обратной теореме Пифагора, ΔВ ₁ С ₁ Е – прямоугольный, угол В ₁ С ₁ Е = 90°

6) Искомое расстояние от точки Е до прямой В ₁ С ₁ – это длина С ₁ Е = 2

1) Поместим призму в прямоугольную систему координат, расположив координатные оси, как показано на рисунке. СС ₁ , СВ и СЕ попарно перпендикулярны, поэтому можно направить вдоль них координатные оси. Получаем координаты:

С ₁ (0;0;1), Е ( ;0;0), В ₁ (0;1;1)

2) Найдем координаты векторов С ₁ В ₁ и С ₁ Е:

С ₁ В ₁ (0;1;0), С ₁ Е ( ;0;-1).

3) Найдем косинус угла между С ₁ В ₁ и С ₁ Е, используя скалярное произведение векторов С ₁ В ₁ и С ₁ Е:

cosβ = = 0 => β = 90° => C ₁ E – искомое расстояние.

4) С ₁ Е = =2

4.6 Расстояние между скрещивающимися прямыми

в пространстве — это длина их общего перпендикуляра. Общий перпендикуляр скрещивающихся прямых — отрезок с концами на этих прямых, перпендикулярный обеим этим прямым.

Если прямые в пространстве пересекаются, расстояние между ними считается равным 0.

Пусть есть не пересекающиеся в пространстве прямые a и b.

Построим плоскости α и β так, чтобы эти плоскости были параллельны, плоскость α содержала в себе прямую a , плоскость β содержала в себе прямую b .

Расстоянием между прямыми a и b будет расстояние между плоскостями α и β .

Александров А.Д. и др

. Геометрия для 10-11 классов: Учеб. пособие для учащихся школ и классов с углубленным изучением математики . Просвещение, 1992.

2. Ю.М.Нейман, Т.М. Королева, Е.Г. Маркарян .

Математика: ЕГЭ: Учебно-справочные материалы «Просвещение», 2011.

3 . Погорелов А.В.

Геометрия: Учеб. для 7-11 кл. сред. шк., 4-е изд. – М.: Просвещение, 1993.

ЕГЭ 2011. Математика. Задача С2. Геометрия. Стереометрия

. Под ред. А. Л. Семенова и И.В.Ященко. МЦНМО, 2011.

Нахождение углов между прямыми и плоскостями (координатно-векторный метод) . Математика в школе. — 2011. — №4.

Угол в правильной шестиугольной призме

На сайте уже были рассмотрены некоторые типы задач по стереометрии, которые входят в единый банк заданий экзамена по математике. Например, задания про составные многогранники .

Призма называется правильной если её боковые перпендикулярны основаниям и в основаниях лежит правильный многоугольник. То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.

Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.

В этой статье для вас задачи на решение призмы, в основании которой лежит правильный шестиугольник . Особенностей и сложностей в решении нет никаких. В чём суть? Дана правильная шестиугольная призма, требуется вычислить расстояние между двумя вершинами или найти заданный угол. Задачи на самом деле простые, в итоге решение сводится к нахождению элемента в прямоугольном треугольнике.

Используется теорема Пифагора и теорема косинусов . Необходимо знание определений тригонометрических функций в прямоугольном треугольнике.

Обязательно посмотрите информацию о правильном шестиугольнике в этой статье (пункт 6) . Ещё вам пригодится навык извлечения квадратного корня их большого числа. Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.

Кратко: что представляет собой правильный шестиугольник?

Известно, что в правильном шестиугольнике стороны равны. Кроме этого, углы между сторонами тоже равны .

*Противолежащие стороны параллельны.

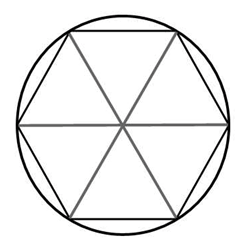
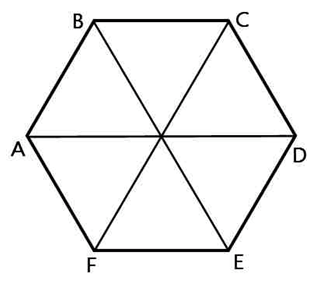
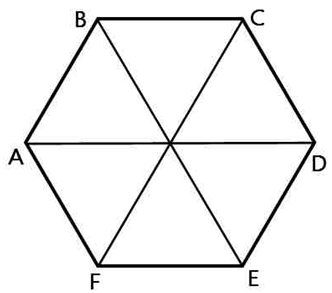
Радиус окружности описанной около правильного шестиугольника равен его стороне. *Это подтверждается очень просто: если мы соединим противоположные вершины шестиугольника, то получим шесть равных равносторонних треугольников. Почему равносторонних?

У каждого треугольника угол при его вершине лежащей в центре равен 60 0 (360:6=60). Так как у треугольника две стороны имеющие общую вершину в центре равны (это радиусы описанной окружности), то каждый угол при основании такого равнобедренного треугольника так же равен 60 градусам.

То есть правильный шестиугольник, образно говоря, состоит как бы из шести равных равносторонних треугольников.

Какой полезный для решения задач факт ещё следует отметить? Угол при вершине шестиугольника (угол между его соседними сторонами) равен 120 градусам.

*Умышленно не коснулись формул правильного N-угольника. Данные формулы мы подробно рассмотрим в будущем, здесь они просто не нужны.

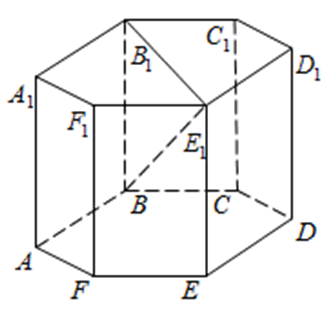
272533. В правильной шестиугольной призме ABCDEFA 1B 1C 1D 1E 1F 1 все ребра равны 48. Найдите расстояние между точками A и E₁.

Рассмотрим прямоугольный треугольник AA 1 E 1 . По теореме Пифагора:

*Угол между сторонами правильного шестиугольника равен 120 градусам.

Отрезок АЕ ₁ является гипотенузой, АА ₁ и А ₁ Е ₁ катеты. Ребро АА ₁ нам известно. Катет А ₁ Е ₁ мы можем найти используя используя теорему косинусов.

Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.

По теореме Пифагора:

*Обратите внимание, что 48 возводить в квадрат совсем не обязательно.

В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 35. Найдите расстояние между точками B и E.

Рассмотрим правильный шестиугольник:

Сказано, что все рёбра равны 35, то есть сторона шестиугольника лежащего в основании равна 35. А так же, как уже сказано, радиус описанной около него окружности равен этому же числу.

273353. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны сорока корням из пяти. Найдите расстояние между точками B и E₁.

Рассмотрим прямоугольный треугольник BB 1 E 1 . По теореме Пифагора:

Отрезок B 1 E 1 равен двум радиусам описанной около правильного шестиугольника окружности, а её радиус равен стороне шестиугольника, то есть

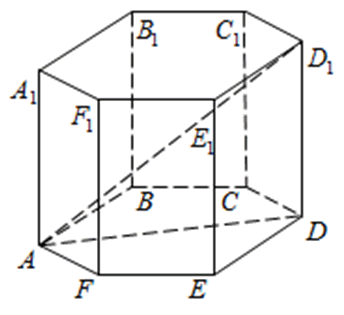
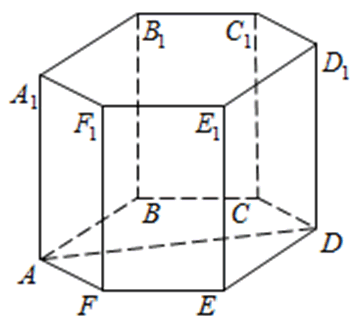
273683. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 45. Найдите тангенс угла AD₁D.

Рассмотрим прямоугольный треугольник ADD₁, в котором AD равно диаметру окружности, описанной вокруг основания. Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне.

В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 23. Найдите угол DAB. Ответ дайте в градусах.

Рассмотрим правильный шестиугольник:

В нём углы между сторонами равны 120°. Значит,

Сама длина ребра не имеет значения, на величину угла она не влияет.

В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 10. Найдите угол AC₁C. Ответ дайте в градусах.

Рассмотрим прямоугольный треугольник AC₁C:

Найдём AC . В правильном шестиугольнике углы между его сторонами равны 120 градусам, тогда по теореме косинусов для треугольника АВС :

Значит, угол AC 1 C равен 60 градусам.

274453. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 10. Найдите угол AC₁C. Ответ дайте в градусах.

Рассмотрим треугольник AС ₁ С, он прямоугольный. Вычислим тангенс указанного в условии угла и определим угол. Известно, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то есть

Катет С₁С = 10. Отрезок АС вычислим по теореме косинусов (это мы уже делали в первой задаче, запишем ещё раз):

В правильном шестиугольнике углы при вершинах равны 120 градусам, то есть

245364. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите расстояние между точками А и Е₁.

245365. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите расстояние между точками В и Е.

245366. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁все ребра равны корню из пяти. Найдите расстояние между точками В и Е₁.

245367. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите тангенс угла AD₁D.

245368. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах.

245369. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите угол AC₁C. Ответ дайте в градусах.

На этом всё! Успеха Вам!

В состав ЕГЭ включены и другие задачи по стереометрии, и они довольно разнообразны. Обязательно будем их рассматривать, не пропустите! Успехов вам!

В правильной шестиугольной призме АBCDEFA1B1C1E1F1 все ребра равны 1. Найдите угол DAB . Ответ дайте в градусах.

• Попроси больше объяснений
• Следить
• Отметить нарушение

Что ты хочешь узнать?

Ответ

Проверено экспертом

Найдите угол DAB — угол правильного шестиугольника ( основания призмы)

Сумма углов многоугольника находится по формуле
180(n-2)
180*(6-2)=720°
Величина одного угла правильного шестиугольника
720:6=120°

Вопрос задан полностью? Иначе призма и ее ребра здесь как будто ни при чем.

Изучением призм занимается пространственная геометрия. Важными их характеристиками являются заключенный в них объем, площадь поверхности и число составляющих элементов. В статье рассмотрим все эти свойства для шестиугольной призмы.

О какой призме пойдет речь?

Призма шестиугольная — это фигура, образованная двумя многоугольниками, имеющими шесть сторон и шесть углов, и шестью параллелограммами, соединяющими отмеченные шестиугольники в единое геометрическое образование.

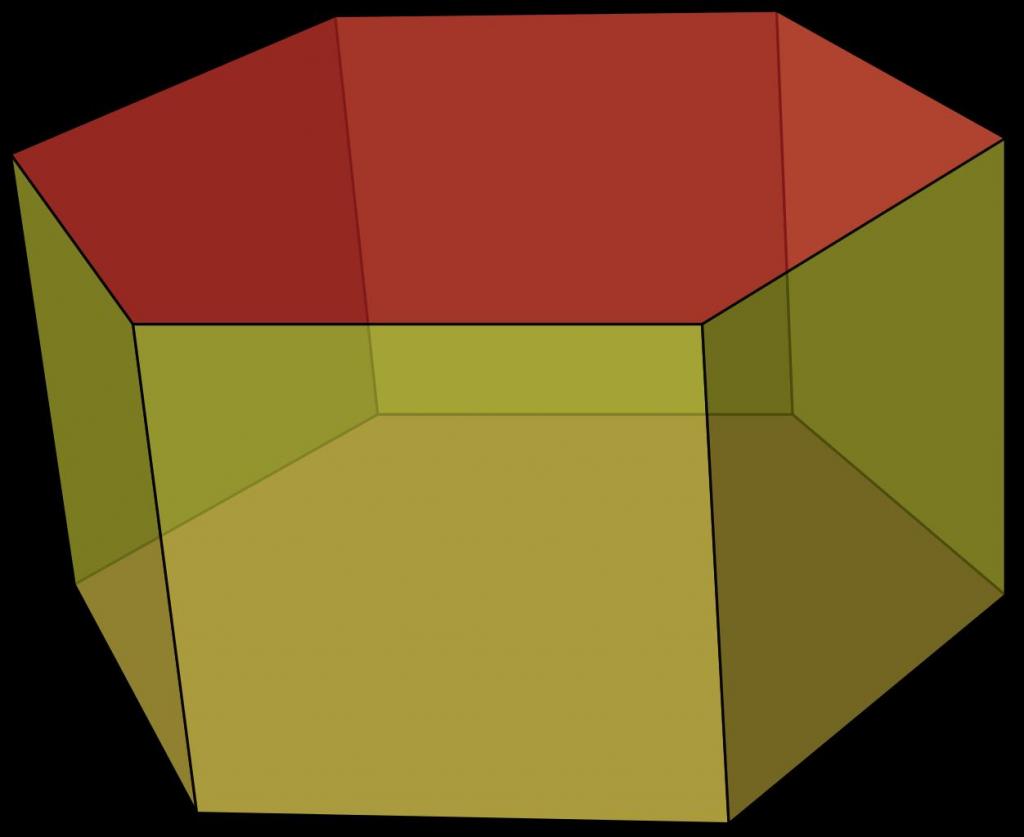
На рисунке изображен пример этой призмы.

Отмеченный красным цветом шестиугольник называется основанием фигуры. Очевидно, что число ее оснований равно двум, причем оба они идентичны. Желто-зеленоватые грани призмы называются ее боковыми сторонами. На рисунке они представлены квадратами, но в общем случае они являются параллелограммами.

Шестиугольная призма может быть наклонной и прямой. В первом случае углы между основанием и боковыми сторонами не являются прямыми, во втором они равны 90 o . Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.

Элементы

Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов. Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).

В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:

число ребер = число граней + число вершин — 2.

Указанные выше цифры удовлетворяют этой формуле.

Диагонали призмы

Все диагонали шестиугольной призмы можно разделить на два типа:

• те, которые лежат в плоскостях ее граней;
• те, которые принадлежат всему объему фигуры.

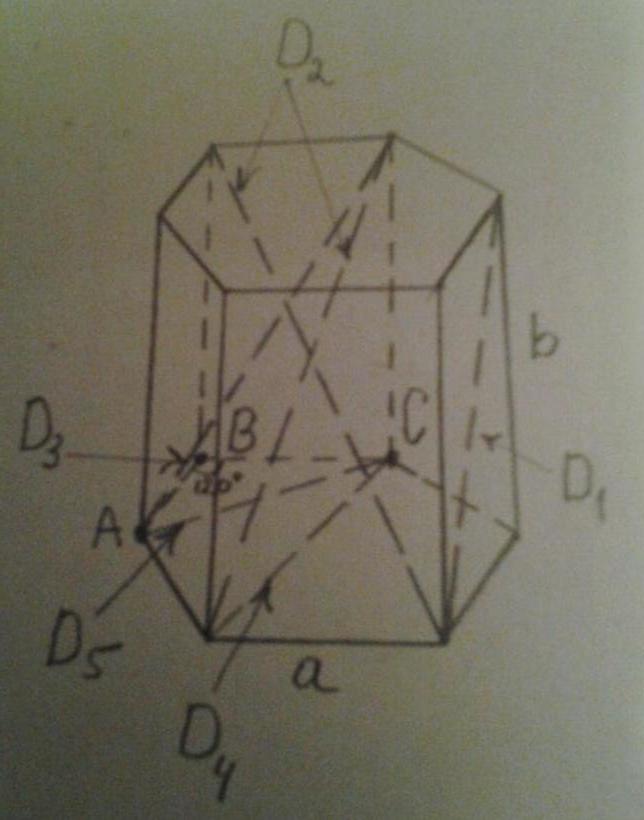
Рисунок ниже показывает все эти диагонали.

Видно, что D₁ — это диагональ боковой стороны, D₂ и D₃ — диагонали всей призмы, D₄ и D₅ — диагонали основания.

Длины диагоналей боковых сторон между собой равны. Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b — длину бокового ребра. Тогда диагональ имеет длину:

Диагональ D₄ также легко определяется. Если вспомнить, что правильный шестиугольник вписывается в окружность радиусом a, то D₄ является диаметром этой окружности, то есть получим следующую формулу:

Диагональ D₅ основания найти несколько сложнее. Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120 o . Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:

Сторона AC является диагональю D₅, поэтому получаем:

Теперь остается найти диагонали D₂ и D₃ правильной шестиугольной призмы. Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:

Таким образом, самой большой диагональю для любых значений a и b является D₂.

Площадь поверхности

Чтобы понять, о чем идет речь, проще всего рассмотреть развертку этой призмы. Она показана на рисунке.

Видно, что для определения площади всех сторон рассматриваемой фигуры необходимо рассчитать отдельно площадь четырехугольника и площадь шестиугольника, затем умножить их на соответствующие целые числа, равные количеству каждого n-угольника в призме, и сложить полученные результаты. Шестиугольников 2, прямоугольников 6.

Для площади прямоугольника получаем:

Тогда площадь боковой поверхности равна:

Для определения площади шестиугольника проще всего воспользоваться соответствующей формулой, которая имеет вид:

Подставляя в это выражение число n равное 6, получаем площадь одного шестиугольника:

Это выражение следует умножить на два, чтобы получить площадь оснований призмы:

Остается сложить S_os и S₂, чтобы получить полную площадь поверхности фигуры:

Объем призмы

После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого. Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:

Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра. Что касается шестиугольной правильной призмы, то значение ее объема является функцией двух переменных: сторон a и b.