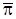Факторизация и эллиптическая кривая. Часть V
К тем сведениям об эллиптических кривых (ЭК), которые доступны читателям Хабра и Интернета в целом, а также из бумажных книг, предлагаю дополнительные, уточняющие важные детали, опущенные в некоторых статьях. Например, в работе приводится изображение тора (рис. 4), но никаких оговорок не делается. Откуда он взялся, почему тор? Другие авторы вообще не упоминают эту фигуру. В чем здесь дело?
Не могу назвать публикацию на Хабре и других сайтах, где автор говорил бы о полях многочленов, хотя обозначение ) таких полей некоторыми авторами и используются, но делается это неправильно. Неприводимый многочлен и примитивный элемент поля и не задаются, что не позволяет читателю построить такое поле и работать с ним, проверить вычислением приводимый результат, если числовой пример вообще приводится. От таких публикаций остается ощущение зря потраченного времени. Такие поля расширения используются в стандартах цифровой подписи и шифрования рядом государств.
Не буду указывать на явные ошибки, читатели в своих комментариях часто сами их указывают, но сделаю попытку высветить общую картину. Попробую перечислить промахи наиболее распространенные и часто повторяемые многими авторами. Практически не называются допущения и ограничения моделей, которые приводятся в публикациях, особенно, когда модель не авторская, а созданная кем-то другим. Важность границ применимости можно не обсуждать — с этим согласны все, но указывается на это авторами исключительно редко.
Пространства изучения моделей
Здесь будем использовать в зависимости от рассматриваемой ситуации различные пространства вещественные и комплексные, аффинные и проективные, бесконечные и конечные подходящей размерности. Поэтому вначале кратко рассмотрим их сущность основные свойства, способы описания. Для практики фактически наибольший интерес представляет конечный случай.
Аффинные пространства 
Рассмотрим множество наборов (а1, а2, …, аn) из n элементов, где каждый аi ∊ F и F некоторое поле. Множество наборов обозначим символом и обычным способом введем для наборов операции сложения и умножения на скаляры. При условии замкнутости множества
по этим операциям оно образует векторное пространство с аддитивным нейтральным элементом О = (0, 0, …, 0).
Для удобства в дальнейшем условимся обозначать набор (а1, а2, …, аn) символами а, в, с…, а будем называть n-мерным аффинным пространством, его элементы – аффинными точками, точку О = (0, 0, …, 0) – назовем началом координат. Если F — конечное поле из
элементов, где р – простое, то
содержит
элементов (наборов, точек). При р = 2 получаем множество всех двоичных чисел разрядности k.
Аффинная плоскость 
Пусть F˟ – конечное алгебраически замкнутое поле и Fо – некоторое подполе поля F˟. Аффинная плоскость под полем F˟ (дискретная конечная F˟×F˟ ) представляет собой множество всех <(α, β)>упорядоченных пар элементов α, β поля F˟. Каждую такую пару Q=(α, β) называют точкой плоскости
, а элементы α, β – координатами точки Q. Если поле F˟ является полем расширения некоторой степени n, то каждая координата точки Q представляет собой многочлен степени не выше n – 1 от формальной переменной t.
Эллиптической кривой (ЭК) над полем F называется плоская гладкая кривая с уравнением вида
Индексы у коэффициентов
в уравнении указывают степени, которые должны быть приписаны этим коэффициентам, чтобы уравнение ЭК стало однородным, т.е. чтобы каждое слагаемое в нем имело общую степень 6.
Через Е(F) обозначают множество, состоящее из точек , удовлетворяющих этому уравнению, с добавлением «бесконечно удаленной» точки О. Если К — некоторое расширение поля F, то через Е(К) будет обозначаться множество, состоящее из точек
удовлетворяющих уравнению ЭК и бесконечно удаленной точки О.
Пример 1. Для поля с характеристикой p = 5 и степенью расширения n = 3 задается примитивный элемент (α) и неприводимый многочлен Порядок поля при этом
, а аффинная плоскость содержит
точек с многочленами в роли координат точек.
Например, задание одной из точек эллиптической кривой в этом поле имеет вид , где многочлены
– координаты точки Q. Малая часть точек такой дискретной плоскости образует ЭК и еще меньшая их часть — является аддитивной группой точек ЭК, которая строится здесь.
Пусть F˟ – алгебраическое замыкание поля поля F. Условие гладкости кривой означает, что в множестве Е(F˟) не существует точек, в которых одновременно обращались бы в нуль частные производные где
Иными словами, система уравнений
не имеет решений, принадлежащих Е(F˟).
Проективное пространство 
Символом по аналогии с предыдущим будем обозначать n-мерное проективное пространство над полем F. Очень важно понимать, как устроено это пространство, и в чем отличие
от
. С этой целью рассмотрим вначале
– множество наборов (ао, а1, …, аn), в котором точка O=(0, 0, …, 0) – начало координат удалена.
Над множеством определим отношение эквивалентности: n–мерная точка а = (ао, а1, …, аn) эквивалентна точке b = (bо, b1, …, bn), если существует такой элемент γ∊F*, где F* – мультипликативная группа поля F, что aо=γbо, a1=γb1. an=γbn. Просто убедиться в том, что все такие пары (a, b) из
образуют отношение (
) эквивалентности, которое индуцирует разбиение множества – на классы эквивалентности.
Все такие классы называются точками пространства и все элементы класса (т.е. сам класс) обозначаются символом [а], если точка а = (ао, а1, …, аn) входит в состав класса, то такая точка а называется представителем класса. В геометрической терминологии все элементы (точки) произвольного класса [а] принадлежат прямой в пространстве
, проходящей через точку а и начало координат в аффинном пространстве.
Пространство образованно
элементами (точками). Это легко показать, так как пространство
имеет
элемент (без нулевого), мультипликативная группа F* поля F˟ состоит из q – 1 элементов (точек проективного пространства). Каждый класс эквивалентности (прямая) порождается произвольным элементом а = (а0, а1, …, аn) умноженным на каждый элемент из F*, т.е. содержит q – 1 элементов.
Тогда число |H˟| классов (их объёмы одинаковы) эквивалентности можно подсчитать по формуле:
Сравнение мощностей n–мерных пространств аффинного и проективного показывает, что | A^n(F) |$» data-tex=»inline»/>.
Пример 2: Пусть . Тогда
– мощность (порядок – число элементов) аффинного пространства
;
— мощность (порядок) аффинного пространства
; в нем |H˟| классов.
— мощность (порядок) проективного пространства
, т.е. число классов эквивалентности точек пространства
. Видим, каждый класс эквивалентности содержит 7 элементов.
| A^n(F) |$» data-tex=»inline»/>. =>585>512.
Проективная плоскость 
Наряду с аффинной плоскостью в криптографии с эллиптическими кривыми используется проективная плоскость. Это связано с тем, что для ЭК, задаваемой в этой плоскости, формулы для групповой операции с точками ЭК не содержат действия деления, т.е. для вычисления координат результирующей точки не требуется обращения элемента в поле F, которая весьма трудоемка. Иногда для проективной плоскости используют обозначение , чтобы подчеркнуть вещественную природу (некомплексную) элементов.
Определение. Приведем в определении тройственное представление проективной плоскости: = <прямые в
, проходящие через начало координат> =
= <отношение вида X: Y: Z>=
= < \<0>/
, где (X: Y: Z), (γХ:γY:γZ), если γ∈R\0>.
В нижней (последней) строчке определения записано фактормножество точек пространства (трехмерного, вещественного) по отношению эквивалентности (
), где γ принадлежит F* -множеству вещественных чисел без нуля, т.е. мультипликативной группе поля.
Рисунок 1 – Аффинная плоскость Z = 1
Легко может быть выполнен переход к произвольному векторному пространству над любым полем. Для того, чтобы представить отношение X: Y: Z для Z = 0, достаточно положить x = X/Z,
y = Y/Z. Этим достигается упрощение, так как исходное отношение задается теперь парой вещественных чисел.
Другими словами, класс эквивалентности троек (x, y, z) по отношению эквивалентности имеет единственного представителя (x, y, 1), третья координата которого Z /Z = 1 для всех точек.
К сожалению, Z все-таки может обращаться в нуль, и в этом случае наш способ представителя класса эквивалентности не годится.
Приведенное рассуждение показывает, что содержит экземпляр пространства
Рисунок 2 – Замены переменных, переводящие кривую в проективное пространство
Прямая общего положения в , проходящая через О, не содержится в плоскости (Z = 0) и, значит пересекает плоскость (Z = 1) в единственной точке, которая и представляет собой этот класс эквивалентности (т.е. прямую L в
). Прямые, лежащие в плоскости (Z = 0), не пересекают плоскость (Z = 1). Следовательно, они соответствуют не точкам из
а асимптотическим направлениям или пучкам параллельных прямых в
. Таким образом, можно представить
как пространство, состоящее из плоскости
, к которой добавлено по одной “точке на бесконечности” для каждого пучка параллельных прямых.
Ньютон занимался и кубическими кривыми, привел их классификацию, им сформулирована Теорема. Для любой неособой кубической кривой существует проективная замена координат, преобразующая кубическую кривую к кривой в форме Вейерштрасса с рациональными а и b. Например, m(m+1)/2=n(n+1)(2n+1)/6 после замены m=(у-9)/18 и n=(x-3)/6 получаем уравнение рациональные корни которого и будут решением задачи.
Приведем кривую к форме Вейерштрасса. Выполним проективную замену координат х = s -t, y = t. Эта замена осуществляет параллельную проекцию плоскости ху на плоскость st. Получаем кривую
. Теперь спроецируем плоскость st на плоскость uv из центра. Еще одна замена координат s=1/3u и t =(6v+1)/6u. Новая кривая (в форме Вейерштрасса) получает вид
Вопрос на понимание ЭК: Какие два натуральных смежных числа при умножении у(у+1) равны произведению трех натуральных смежных чисел (х-1)х(х+1)? В уравнении есть как в ЭК.
Формулы групповой операции ЭК в проективном пространстве (плоскости).
Пусть задано уравнение ЭК в проективной плоскости в форме Вейерштрасса Е(GF(q)):
над полем характеристики р, (р ≠ 2 и р ≠ 3), получаемое путем перевода ЭК из аффинной в проективную плоскость. Точки такой ЭК можно рассматривать как эквивалентный класс точек (X, Y, Z) плоскости над полем GF(q).
Бесконечно удаленная точка O ,O ∈ представляет все ненулевые точки с отношением эквивалентности (X, Y, Z)
(kX, kY, kZ). Такие точки обозначаются как (X, Y, Z) и среди них имеется единственная точка с координатой Z = 0 – это точка (0, 1, 0). При Z = 0 обязательно и Х = 0, и существует только один класс эквивалентности с Х = Z = 0, содержащий бесконечно удаленную точку (0, 1, 0)∈ Е(GF(q))∈ .
Существует возможность и обратного перевода ЭК из пространства в аффинное пространство
. Для всех точек Q = (X, Y, Z) ≠ O производится замена (X, Y, Z) = (Х/Z, Y/Z, 1). При этом выполняется однозначное соответствие: точке (х = Х/Z, y = Y/Z) соответствует точка (X, Y, Z).
Формулы удвоения точки ЭК в проективном пространстве принимают вид:
,
где координата кратна λ.
Последующие преобразования обеспечивают получение формул группового сложения точек ЭК в проективных координатах.
Суммирование пары различных точек группы ЭК в проективном пространстве соответствует некоторой третьей точке этой группы, имеющей три координаты. Так третьей координатой является
, а весь набор получает вид
При рассмотрении ЭК над расширенным полем , имеющих инвариант j ≠ 0 формулы принимают иной вид для случая
Комплексное пространство C
Эллиптическую кривую можно рассматривать не только в аффинном, проективном, но и в комплексном пространствах. В последнем случае точки ЭК называются комплексными точками. Далее будем рассматривать именно такие точки над комплексными полями.
Поскольку ЭК – это плоская кривая, то ограничимся рассмотрением комплексной проективной плоскости . В этой плоскости можно задавать функции, которые имеют два линейных независимых периода. Их называют мероморфные двоякопериодические функции с периодами ω1, ω2.
По причине линейной независимости периодов над R, ω1/ω2∈R. Другое название для таких функций – эллиптические функции. Для наших целей интерес представляет функция Вейерштрасса ℘(z), которая удовлетворяет дифференциальному уравнению вида
где – некоторые константы, зависящие от периодов ω1, ω2.
Сходство записанного уравнения с ЭК весьма значительное.
Зададим на плоскости С решетку Λ=
Позднее покажем, что элементы факторгруппы можно отобразить в комплексные точки Е(С) ЭК Е, и такое отображение взаимно однозначно.
Многочлен правой части ЭК над комплексной плоскостью С.
Параметризацию удаётся осуществить для части ЭК на С, благодаря выбору необходимой функции ℘.
В проективной комплексной плоскости с учетом полюсов функции ℘ параметризация устанавливает взаимно однозначное соответствие между множеством точек C/Λ и множеством Е(С) комплексных точек кривой Е. Такое соответствие оказывается биголоморфно.
Суммирование комплексных чисел определяется групповым законом сложения на торе C/Λ. Ниже будет показано, что соответствие φ: C/Λ→Е(С) ЭК Е. Далее выясняется, что любая ЭК на С может быть нормализована подбором подходящей функции Вейерштрасса ℘. В основе процедуры прояснение такой связи лежит возможность обращения эллиптических интегралов.
Эллиптические функции
Определение. Алгебраическую кривую называют эллиптической, если она как одномерное комплексное многообразие представляет собой тор (бублик).
Определение. Мероморфная двоякопериодическая функция называется эллиптической.
Определение. Аналитическая функция называется мероморфной, если у нее в конечной области С нет особых точек, отличных от полюсов.
Определение. Функция:f^C →С∪( <∞>называется двоякопериодической с периодами ω1, ω2 при линейной независимости периодов над R и f(z+ω1)=f(z)=f(z+ω2) для любых z∈C.
Двоякопериодическую функцию называют эллиптической, если она мероморфна. Множество эллиптических функций образует поле при фиксированных периодах ω1, ω2. В плоскости С точки 0, ω1, ω2 и ω1+ω2 образуют вершины параллелограмма
П=<α1ω1+α2ω2|0 ≤α1,α2 ≤1>, который называется фундаментальным. Стороны, сходящиеся в точке 0 и сама точка принадлежат П, а три другие вершины и две стороны — не принадлежат П.
Особый интерес представляет фундаментальный параллелограмм и его граница.
Определение. Фундаментальным параллелограммом называется область плоскости С, заданная соотношением П = <α1ω1+α2ω2|0 ≤α1,α2 ≤1>где α1,α2∈R.
Параллелограммом периодов называется любой параллелограмм вида α+П, α∈С. Для всех таких параллелограммов справедливы одинаковые условия.
Относительно эллиптических функций Ж. Лиувиллем (1809-1882) сформулированы и доказаны следующие результаты.
Теорема 1. Не существует отличных от констант целых эллиптических функций.
Доказательство. Целая эллиптическая функция непрерывна, так как не имеет полюсов; поэтому она ограничена на замыкании П. В силу периодичности функция ограничена на С, следовательно, она постоянна.
Следствие 2. Две эллиптические функции, имеющие одинаковые наборы полюсов и соответственно равные главные части в полюсах, отличаются на константу.
Теорема 3. Если эллиптическая функция f(z) не имеет полюсов на границе L параллелограмма П+α, то сумма вычетов f(z) во всех полюсах, лежащих внутри П+α, равна 0.
Эллиптическая функция Вейерштрасса. Эта функция играет важную роль для всей теории эллиптических функций в силу ее замечательных свойств. Займемся рассмотрением этих свойств подробнее и выясним, как и какие из них могут быть использованы для наших целей, связанных с изучением ЭК. Функция Вейерштрасса определяется над комплексной плоскостью C и представляется формулой.
,
где Λ не содержит точку 0, т.е. решетка периодов с удаленной точкой 0 и фиксированными значениями ω1, ω2. Выражение под знаком суммы нельзя записывать через две суммы, так как каждая из них представляет расходящийся ряд.
Комплексная плоскость C с решеткой Λ
Перейдем к рассмотрению комплексного случая ЭК.
Пусть ω1 и ω2 — два линейно независимых на R комплексных числа. Обозначим через
Λ=
На рисунке заштрихованная часть комплексной плоскости представляет собой фундаментальную область – параллелограмм, сдвиги которого на элементы из Λ накрывают всю плоскость С.
Рисунок 3. Фундаментальный параллелограмм в комплексной плоскости
Фактор-пространство С/Λ можно представить в виде фундаментального параллелограмма с отождествленными противоположными сторонами. Так как сложение комплексных чисел (x,y) → x+y задает некоторое голоморфное отображение C×C→C, то С является комплексной группой Ли, а Λ – ее подгруппой. Таким образом, фактор-пространство С/Λ – компактная комплексная группа Ли.
Пару (ω1, ω2) можно умножить на комплексное число или
и получить пару, состоящую из 1 и τ, где Imτ>0. Соответствующую решетку, порожденную 1 и τ обозначим через Λτ, а фактор-пространство С/Λτ через Eτ. Каждое пространство С/Λ изоморфно одному из Eτ, причем Eτ и E’τ изоморфны тогда и только тогда, когда
Функции на С/Λ. Пусть g – мероморфная функция на С/Λ. Тогда q∙g – мероморфная функция на С, удовлетворяющая условиям q·g(z+ω1) = q·g(z+ω2) = q·g(z)
Таким образом, q∙g – двоякопериодическая мероморфная функция на С. Обратно, каждая двоякопериодическая мероморфная функция на С (так называемая эллиптическая функция) определяет некоторую мероморфную функцию на С/Λ.
Основная эллиптическая функция может быть представлена в виде ряда:
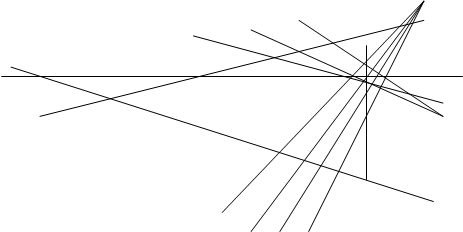
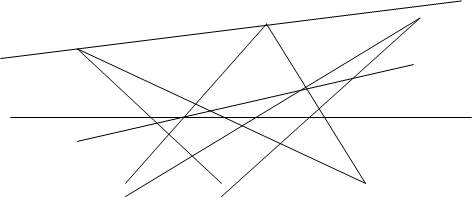
Рисунок 4 – Представление ЭК в области фундаментального параллелограмма тороидальной поверхностью
На рис. 4 изображен тор, слева развертка его поверхности (плоский лист-прямоугольник). Развертка получена двумя перпендикулярными разрезами тора: вертикальным (в сечении дает малую окружность — торцы цилиндрической поверхности) и горизонтальным вдоль образующей цилиндра, получаемого после первого разреза, и распрямления (топология) вдоль осевой линии. Линии разрезов: первая совмещается с координатной осью ординат (у), вторая — границы (верхний и нижний края развертки) равноудаленные от оси абсцисс (х). Все целочисленные точки группы ЭК в этой системе координат получают вид (х, у).
Действительно, на рисунке видим симметричное относительно оси х расположение точек. Сплошная линия на торе (синяя) без разрывов на развертке представлена 4-я отрезками, концевые точки которых соответственно имеют совпадающие координаты. Другими словами, обратными действиями (склейкой) можно получить объемную фигуру — тор, на поверхности которого все отрезки прямых воссоединятся в замкнутую пространственную винтовую линию. Условность этой иллюстрации в том, что плоская ЭК представляется в комплексной плоскости двоякопериодической функцией, удовлетворяющей уравнению Вейерштрасса.
Эта функция мероморфна на С, двоякопериодическая и имеет полюсы кратности 2 в точности в вершинах решетки Λ. Очевидно, что и производная ℘’(z) является двоякопериодической функцией, имеющей полюсы кратности 3 в вершинах решетки Λ.
℘(z) и ℘′(z) связаны между собой некоторым полиномиальным соотношением:
f(℘(z), ℘′(z), 1) = 0.
Факторизация из полезных возможностей ЭК
— разложение составного числа N на множители.
Формально алгоритм, предложенный Ленстрой содержит следующие шаги.
ш1. Выбирается ЭК над полем порядка N, т.е. целые числа из диапазона .
ш2. Рассматриваем кубическую кривую и базисную точку ЭК
.
ш3. Вычисляем ; этим проверяется являются ли редукции кривой Е эллиптическими. Если НОД =N, переход к Ш1 и выбор нового b. Если
, то получен нетривиальный делитель числа N. При
, переход к Ш4
ш4. Выбираем число k, являющееся произведением небольших простых чисел в небольших степенях: k=НОК(2,3, . М), где М-натуральное число.
ш5. Вычисляем кратную базисной точку
ш6. Вычисляем . Если 1 Список использованной литературы
Реферат: Различные подходы к определению проективной плоскости
| Название: Различные подходы к определению проективной плоскости Раздел: Рефераты по математике Тип: реферат Добавлен 03:03:07 24 марта 2008 Похожие работы Просмотров: 1557 Комментариев: 22 Оценило: 3 человек Средний балл: 4.3 Оценка: неизвестно Скачать | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |
Проверим выполняемость аксиом проективной плоскости.
1)j- сюрьективно, так как у » прямой ОМ всегда будет хотя бы один прообраз вектор m // ОМ
2)если 2 вектора коллинеарны a //a 1, то образы совпадают — это будет прямая ОА, j(a )=j(a 1)=OA.
Если образы 2-х векторов совпадают, то векторы коллинеарны.
Построенная конструкция является моделью проективной плоскости. Роль проективных точек в этой модели выполняют прямые связки, с роль проективных прямых выполняют плоскости связки.
Проанализируем, как выполняются свойства проективной плоскости.
| Свойства проективной плоскости | Реализация на модели | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||
 | |||
 | |||
j- биективно? т.е. любой ли прямой связки будет соответствовать прообраз? Ответ: нет. Прямые связки параллельные p не имеют прообразов и такие прямые называют особыми. Таких прямых будет бесчисленное множество и все они лежат в плоскости связки, которая параллельна p. Такую плоскость назовем особой плоскостью. Для того, чтобы отображение j сделать биективным и получить новую модель проективной плоскости дополним евклидову плоскость p «несобственными элементами».
Рассмотрим особую прямую связки m , m //p, и проведем через эту прямую не особую плоскость a, a(m )Çp=a , a //m .
» прямая (не особая прямая) связки Îa имеет свой прообраз на прямой a .
Поставим в соответствие прямой m не собственную ()М ¥, которая Îa .
 |
Проведем через особую прямую m другую не особую плоскость bb(m )Çp =b , a //b //m, так как каждая не особая прямая b имеет прообраз на прямую b , то прообраз особой прямой m не собственная ()М¥Îb . Если рассмотрим другую особую прямую n , то должны поставить в соответствие свою несобственную ()N¥.
Каждая не особая плоскость связки имеет на плоскости p своим прообразом прямую пересечения этой плоскости с плоскостью p.a-a , b-b . Поставим в соответствие особой плоскости несобственную прямую l ¥, тогда так как все особые прямые лежат в единственной особой плоскости, то все несобственные точки лежат на единственной несобственной прямой.
Определение: Расширенной евклидовой плоскостью p называется евклидова плоскость дополненная несобственными элементами: несобственными точками и единственной несобственной прямой, причем все прямые параллельные между собой дополняются одной и той же несобственной точкой и все несобственные точки лежат на единственной несобственной прямой.
Отображение j: p® связку стало биективным, так как связка прямых является моделью проективной плоскости, то и расширенная плоскость pявляется моделью проективной плоскости. Роль проективных точек в этой модели выполняют собственные и несобственные точки. Роль проективных прямых выполняют собственные прямые плоскости p и несобственная прямая.
Рассмотрим выполняемость свойств проективной плоскости на построенной модели.
| Свойства проективной плоскости | Выполнение свойств на модели | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
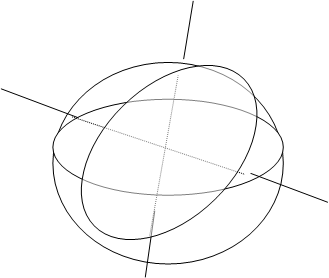 |
Рассмотрим связку с центром в ()О и зададим отображение j:A®íA’,A»ý (прямой связки соответствует пара диаметрально противоположных точек пересечения этой прямой со сферой). j — биективно Þ построенная конструкция является моделью проективной плоскости.
Проверим выполняемость свойств проективной плоскости.
1)Через » две точки проходит единственная прямая
— через две пары диаметрально противоположных точек сферы íМ’,М»ý и íN’,N»ý проходит единственная окружность большого радиуса.
2)» две прямые проективной плоскости пересекаются
-» две окружности большого радиуса пересекаются в диаметрально противоположных точках.
3)$ три точки не лежащие на одной прямой
-$ три пары диаметрально противоположных точек Ï одной окружности большого радиуса. Например: точки N=
4)На каждой прямой лежит не менее трех точек
-рассмотрим окружность большого радиуса через ()О можно провести три различных диаметра, каждый диаметр пересекает данную окружность в диаметрально противоположных точках. Это означает, что на каждой прямой лежит не менее трех точек.
1.4. Теорема Дезарга.
При данном способе построения проективной плоскости имеет место теорема Дезарга, которая гласит:
Теорема: Если прямые проходящие через соответствующие вершины двух трехвершинников пересекаются в одной точке, то точки пересечения соответствующих сторон этих трехвершинников лежат на одной прямой.
P,Q,R- лежат в одной прямой?
Рассмотрим векторы O,A,A’,B ,B ‘,C,C’,P,Q,R порождающие соответствующие (), так как А,А’,О лежат на одной прямой, то векторы порождающие их линейно зависимы, т.е. O= a A + a ‘A’.
Из того, что В’, В, О — лежат на одной прямой Þ В, В’, О- линейно зависимы ÞO= bB + b ‘B ‘
()С, С’, О — лежат на одной прямой ÞO= c C + c ‘C’
А,В,Р — линейно зависимы Þ () А,В,Р Î одной прямой, А’,В’,Р’- линейно зависимы Þ()А’,В’,Р’ Î одной прямой.
А,С,Q- линейно зависимы Þ()А,С,QÎ одной прямой.
А’,С’,Q’- линейно зависимы Þ()А’,С’,Q’ Î одной прямой.
В,С,R –линейно зависимы Þ()В,С,RÎ одной прямой.
В’,С’,R’ –линейно зависимы Þ()В’,С’,R’ Î одной прямой
Составим выражение:
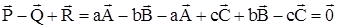
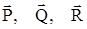
Принято называть трехвершинники, удовлетворяющие теореме Дезарга, дезарговыми. ()О=АА’ÇВВ’ÇСС’- дезарговой, прямую, которой принадлежат точки P,Q,R — дезарговой. Для теоремы Дезарга имеет место обратная теорема:
Если точки пересечения соответственных сторон двух трехвершинников лежат на одной прямой, то прямые, проходящие через соответственные вершины этих трехвершинников, проходят через одну точку.
|

 |
А,В,С- вершины прямые АВ,ВС,АС- стороны
1.5. Теорема Паппа.
Следующей составляющей данной теории является теорема Паппа- Паскаля, которая является частным случаем теоремы Паскаля. Сформулируем теорему Паскаля.
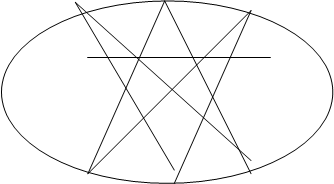 |
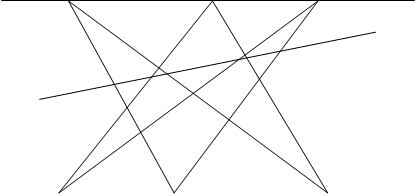
Теорема Паскаля: Для того, чтобы шесть точек, из которых никакие три не лежат на одной прямой принадлежали овальной кривой, необходимо и достаточно, чтобы точки пересечения соответствующих сторон шестивершинника* лежали на одной прямой. AB’ÇA’B=P,AC’ÇA’C=Q, BC’ÇB’C=R.(рис. 1)
P,Q,R принадлежат прямой (прямая Паскаля)
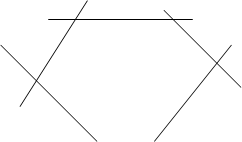
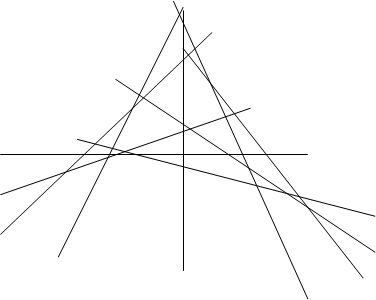
Рассмотрим теорему Паскаля в том частном случае, когда кривая второго порядка распадается на пару прямых. Пусть А,В,С,А’,В’,С’- шесть вершин шестиугольника Паскаля, расположенных по три на данных прямых l и l ‘ , которые мы рассматриваем как распавшуюся кривую второго порядка (рис 2). Тогда имеем следующие три точки пересечения пар соответствующих сторон шестиугольника: Р=АВ’ÇА’В, Q=А’СÇАС’, R=ВС’ÇВ’С. По теореме Паскаля эти три точки лежат на одной прямой. Рассмотренный частный случай теоремы Паскаля был известен древним греческим геометрам и носил название теоремы Паппа. Теперь эта теорема носит название Паппа — Паскаля.
 |


 |
 |
 |
Мы рассмотрели один из подходов к определению проективной плоскости, а именно определения проективной плоскости на базе трехмерного векторного пространства.
Теперь рассмотрим аналитическое определение проективной плоскости.
Глава 2. Аналитическое построение проективной плоскости.
2.1. Понятие проективной плоскости.
Определение 1: Проективной точкой называется класс пропорциональных троек действительных чисел, не содержащих нулевой тройки.
Будем обозначать его Х=
Множество всех проективных точек называется действительной проективной плоскостью.
Определение 2: Проективной прямой называется множество всех точек удовлетворяющих линейному однородному уравнению вида:
С1Х 1+ С2Х 2+ С3Х 3=0 (1)
где хотя бы одно из чисел Ci отлично от нуля.
Определение 2 корректно, так как если тройка (Х1,Х2,Х3) удовлетворяет уравнению (1), то в силу его однородности при любом действительном l тройка (lХ1, lХ2, lХ3) удовлетворяет уравнению (1).
Точки, удовлетворяющие уравнению (1) удовлетворяют также линейному однородному уравнению.
(mС1)Х 1+ (mС2)Х 2+ (mС3)Х 3=0 (2)
Поэтому каждой прямой, заданной уравнением (2) можно поставить во взаимно однозначное соответствие класс пропорциональных троек С=<(С1,С2,С3)>. Так, что тройками из одного класса соответствует одна прямая, причем этот класс не содержит нулевой тройки. Ввиду этого прямую, заданную уравнением (2) будем обозначать той же буквой С, что и соответствующий класс <(С1,С2,С3)>.
Равенство (2) можно записать также в виде
Скалярное произведение троек С и Х. СХ= C1Х1 + С2Х2 + С3Х3 =0
Замечание : Рассмотрим 3-мерное линейное пространство L3. Исключим из него нулевой вектор 0. Множество L3\ <0>разобьем по классам эквивалентности так, что векторы одного класса коллинеарны между собой. Каждый такой класс назовем проективной точкой, а множество всех классов 2-мерным проективным пространством (плоскостью). Множество всех классов, векторы которых принадлежат \ <0>назовем одномерной проективной плоскостью (прямой).
В L3 введем координаты. Тогда каждому вектору соответствует строка (Х1,Х2,Х3), а каждому классу эквивалентности из L3\ <0>(т.е. проективной ())- класс <(Х1,Х2,Х3)>пропорциональных строк, не содержащий нулевой строки.
Мы пришли к определению проективной плоскости.
2.2. Свойства проективной плоскости.
Докажем несколько простых теорем о взаимном расположении () и прямых на проективной плоскости.
Теорема 1: Через две различные () проходит единственная прямая.
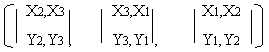
так как CХ = (Х*Y)Х = |Х,Y,Х| = 0
CY = (Х*Y)Y = |Х,Y,Y| = 0
и по свойству определителей, то () Х и Y принадлежат прямой С.
2) Единственность. Если прямая С= <(C1,C2,C3)>содержит () Х и Y, то любой представитель (C1,C2,C3) класса С удовлетворяет системе уравнений.
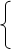
C1Y1 + C2Y2 + C3Y3 =0 (5)
$ бесконечное множество ненулевых решений этой системы (нулевое решение не определяет прямую). При этом для » решения (С1,С2,С3) справедливо равенство:

Y2,Y3 , Y3,Y1 , Y1,Y2
Т.е. решения системы (5) образуют единственный класс ненулевых троек. Этот класс определяет единственную прямую С. ч.т.д.
Теорема 2: Две различные прямые имеют единственную общую точку.
Доказательство: Пусть, С=<(С1,С2,С3)>, m=<(m 1,m 2,m 3)> две различные прямые. Найдем () Х =<(Х1,Х2,Х3)>, лежащую на этих прямых. Достаточно повторить доказательство предыдущей теоремы, заменив Х на С, Y на m , С на Х. Получим, что единственная общая точка Х определяется равенством
Теорема 3: Для того, чтобы три () Х,Y,Z лежали на одной прямой, необходимо и достаточно, чтобы


|X,Y,Z|=0 (7), то есть Y1 Y2 Y3 =0
Доказательство: 1)Необходимость. Пусть () X,Y,Z лежат на одной прямой С. если хотя бы две из них совпадают, то равенство (7) следует из определения смешенного произведения и свойств определителя. Пусть эти () различны. Пользуясь теоремой 1, можно записать C=X*Y. Так как ()Z лежит на прямой C, то CZ=0 Þ (X*Y)Z=|X,Y,Z|=0
2)Достаточность. Пусть выполняется равенство (7). Рассмотрим произведение C=X*Y. Равенство (7) можно записать в виде (X*Y)Z=0, то есть CZ=0 Þ()z лежит на прямой C проходящей через () X и Y. Равенство (7) не зависит от выбора представителей точек.
Теорема 4: Для того, чтобы три прямые c, m, n проходили через одну () необходимо и достаточно, чтобы
Для троек действительных чисел понятие линейной зависимости и линейной независимости определяется так же, как и для векторов. Пусть тройки x,…, x линейно зависимы. Легко проверить, что » другие тройки x,…, x, принадлежащие тем же классам, тоже линейно зависимы. Поэтому классы троек (точки) линейно зависимы, если линейно зависимы какие-нибудь представители этих классов.
Из теорем 3 и 4 следуют две теоремы.
Теорема 5: Для того, чтобы три () лежали на одной прямой, необходимо и достаточно, чтобы они были линейно зависимы.
Теорема 6: Для того, чтобы три прямые проходили через одну (), необходимо и достаточно, чтобы они были линейно зависимы.
2.3. Теорема Дезарга.
На проективной действительной плоскости имеет место теорема Дезарга.
Теорема Дезарга : Если прямые проходящие через соответствующие вершины двух трехвершинников пересекаются в одной точке, то точки пересечения соответствующих сторон этих трехвершинников лежат на одной прямой.
P=ABÇA’B’, Q=ACÇA’C’, R=BCÇB’C’, AA’ÇBB’ÇCC’=Q
P,Q,R лежат на одной прямой.

 |
Координаты ()А’- есть линейная комбинация координат ()А и ()О, так как А¹А’, то а’=aА + dq
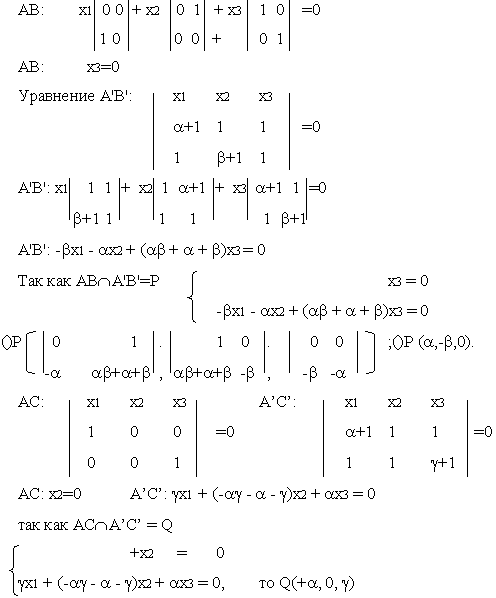 |
Можно положить d=1. Тогда получаем А’=aА +q. Тоже самое относится и к другим вершинам трехвершинника A’B’C’. Поэтому А'(a+1,1,1), В'(1,b+1,1), С'(1,1,g+1) уравнение прямой АВ:
так как R= BCÇB’C’
С помощью условия коллинеарности трех () убедимся, что () P,Q,R лежат на одной прямой.

Условие коллинеарности выполнено, следовательно, P,Q,RÎ одной прямой.
Глава 3. Аксиоматическое построение проективной плоскости.
3.1. Аксиоматика аффинной плоскости.
Начнем с некоторых наиболее простых фактов обычной плоской геометрии, которые мы применим в качестве аксиом при синтетическом построении теории.
Определение : Аффинной плоскостью называют множество элементов, именуемых точками и систему его подмножеств, именуемых прямыми, причем должны выполнятся три формулируемые ниже аксиомы А1-А3.
А1: Для » двух различных точек Р и Q$ единственная прямая, проходящая через них.
Две прямые называются параллельными, если они совпадают или не имеют общих точек.
А2: Для » заданной прямой l и точки Р $ одна и только одна проходящая через Р прямая m : m || l
А3: $ три неколлинеарные точки (Точки Р1,Р2,…Рn называются коллинеарными, если $ прямая l , что все эти точки ей принадлежат).
Пример: Евклидова плоскость Е2 удовлетворяет аксиомам А1-А3, то есть является аффинной плоскостью.
Пример: Аффинная плоскость имеет, по крайней мере, четыре различных точки; плоскость состоящая ровно из четырех () существует.
Действительно в силу А3 на плоскости есть три неколлинеарные точки; обозначим их через P ,Q,R. Согласно А2, $ прямая l , проходящая через Р и параллельной прямой QR, соединяющей Q и R (эта прямая $ по А1). Точно так же доказывается $ прямой
m || P Q, проходящей через R.
Покажем теперь, что l || m .
же S¹R. Таким образом, четвертая () S необходимо должна существовать и наше первое утверждение доказано.
 |
Теперь рассмотрим прямые P R и QS. Они могут пересекаться, но они могут и не пересекаться — это не противоречит аксиомам.
В этом случае мы получаем аффинную плоскость, содержащую ровно четыре () P ,Q,R,S и шесть прямых P Q,РR,P S,QR,QS,RS.
Аксиомы А1-А3 здесь выполняются, таким образом, мы получим аффинную плоскость 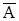
3.2. Аксиоматика проективной плоскости.
Определение : Проективной плоскостью S называют множество, элементами которого именуются точками, и набор его подмножеств, именуемых прямыми, если при этом выполняются следующие четыре аксиомы.
П1.Через две различные точки P и Q плоскости S можно провести единственную прямую.
П2. » две прямые пересекаются по меньшей мере в одной точки.
П3. $ три неколлинеарные точки.
П4. Прямая содержит, по меньшей мере, три точки.
3.3. Модели проективной плоскости.
1)Рассмотренная ранее расширенная евклидовая плоскость есть модель проективной плоскости.
Доказательство: Проверим выполнение четырех аксиом П1-П4.
П1. Пусть P и QÎ
1. Если Р и Q — собственные (), то через них можно провести только одну прямую.
2. Если Р — собственная точка p, а Q- несобственная точка, то по аксиоме А2 $ прямая m , такая, что РÎm и m || l , так , что QÎ пополнению прямой m до прямой из p. Прямая m -единственная прямая p, проходящая через Р и Q.
3. Если Р и Q несобственные (), то через них проходит единственная несобственная прямая.
П2. Пусть заданы прямые l и m .
1.Если l и m — несобственные прямые и l || m , то они пересекаются в некоторой точке. Если l || m , то они пересекаются в несобственной точке Р¥.
2.Если l — собственная прямая, а m — несобственная прямая, то они пересекаются в несобственной точке Р¥.
П3. Непосредственно следует из А3. Необходимо только проверить, что если Р и Q и R неколлинеарны в А, то они не будут коллинеарны в p. Действительно, в p$ только одна (несобсвтенная) прямая, не принадлежащая А, но () Р,Q,R ей не принадлежат.
П4. Каждая прямая плоскости А содержит хотя бы две (). Но в p каждая прямая содержит еще и несобственную точку, поэтому она содержит не менее трех точек.
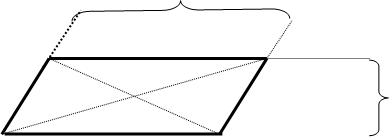
2) Пополняя аффинную плоскость А из четырех (), мы получим проективную плоскость S1 из семи точек.
Докажем это: Проверим выполнение четырех аксиом П1-П4.
 | ||
 | ||
Определим () пересечения прямых АВÇCD=N ¥, BCÇAD=M ¥, АCÇBC=P ¥N ¥, P ¥, M ¥Î одной несобственной прямой.
П1. Через две различные () плоскости можно провести единственную прямую.
Если А,В — собственные (), то через них можно провести только одну прямую из А. () А,В Î несобственной прямой, поэтому и в S1 через них можно провести единственную прямую.
Рассмотрим А- собственная () и N ¥- несобственная (). Через эти точки проходит единственная прямая, так как () N ¥ определена как пересечение прямых АВ и CDÞN ¥ÎАВ.
Пусть имеем не собственные точки, через них проходит несобственная прямая S1 и она единственная.
П2. » две прямые пересекаются по меньшей мере в одной точке.
Справедливость аксиомы П2 следует из определения S1.
П3. $ три неколлинеарные точки.
Непосредственно следует из построения аффинной плоскости А. А мы дополнили точками N ¥, P ¥, M ¥ (несобственными, которые принадлежат одной несобственной прямой). И поэтому точки не коллинеарные в А будут неколлинеарные в S1.
П4. Каждая прямая плоскости А содержит хотя бы две точки. В S1 каждая прямая содержит несобственную точку. Следовательно прямая в S1 содержит не менее трех точек.
Все аксиомы проективной плоскости выполняются, следовательно, S1 — проективная плоскость.
3) Связка прямых евклидова трехмерного пространства — модель проективной плоскости, построенной на аксиомах П1-П4.
3) Действительная проективная плоскость (множество упорядоченных троек действительных чисел, одновременно не равных нулю), рассмотренная ранее, удовлетворяет аксиомам П1-П4.
3.4. Теорема Дезарга.
Одним из важных результатов проективной геометрии является теорема Дезарга, которая утверждает следующее:
П5 (теорема Дезарга)

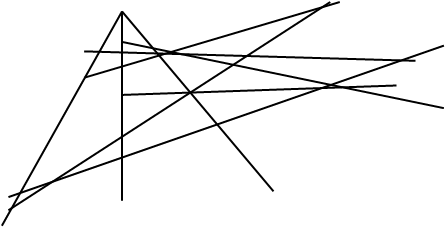 |
P ,Q,R лежат на одной прямой.
В рамках теории, которую мы строим, не совсем правильно называть это утверждение “теоремой”, потому что нельзя доказать, исходя только из аксиом П1-П4. Примем это утверждение за аксиому П5. Хотя при первом и втором способе построения проективной плоскости это утверждение выступает как теорема.
Покажем, что П5 не есть следствие П1-П4, а именно, построим геометрию, удовлетворяющую аксиомам П1-П4, но не удовлетворяющую П5.
Определение : Конфигурацией называют множество элементов, именуемых точками, и набор его подмножеств, именуемых прямыми, если при этом выполняется аксиома.
К1. Две различные () принадлежат не более чем одной прямой.
Отсюда следует, что две различные прямые имеют не более одной общей точки
Примеры: Любая аффинная и » проективная плоскость являются конфигурациями. Набор 10 точек и 10 прямых теоремы Дезарга — тоже конфигурация.
Пусть p0- некоторая конфигурация. Мы определим свободную проективную плоскость П, порожденную p0.
Пусть p1- новая конфигурация, определенная следующим образом. Точками p1 являются точки p0. Прямыми p1 являются все прямые p0; кроме того, каждая пара точек Р1, Р2Îp0 не принадлежащая прямой из p0, задает новую прямую
í Р1, Р2ý из p1. Тогда p1 обладает следующим свойством;
а) » две различные ()p1 принадлежат одной прямой. Построим p2, исходя из p1, следующим образом. Точками p2 служат все точки p1; кроме того, каждая пара непересекающихся прямых l 1,l 2 задает новую точку l 1Çl 2. Прямыми p2 служат прямые p1, пополненные новыми точками; например, () l 1Çl 2 Î дополненным прямым l 1 и l 2. Тогда p2 обладает следующим свойством.
б) » две различные прямые имеют общую точку; продолжим это построение. Для четных n мы построим pn +1 из pn , добавляя к прямым pn новые прямые; для нечетных n мы построим pn +1 из pn , добавляя к () pn новые точки.
Пусть теперь П= Èpn
Элементы конфигураций pn мы назовем точками П; далее, прямой П мы назовем подмножество L ÍП, такое, что LÇpn есть прямая из pn для всех достаточно больших n .
Предложение 1 : Если p0 содержит по меньшей мере четыре точки, никакие три из которых не принадлежат одной прямой, то П — проективная плоскость.
Доказательство: pn удовлетворяет б) для четных n и удовлетворяет а) для нечетных n Þ на П выполняются оба свойства а) и б), то есть П удовлетворяет П1 и П2. Если P ,Q,R неколлинеарны на p0, значит, П3, тоже выполняется.
Покажем, что в П каждая прямая содержит хотя бы три точки.
Каждая прямая из П определяется двумя точками.
По П2: » две прямые имеют общую ()
Получим, каждая прямая содержит хотя бы три точки.
Все аксиомы проективной плоскости выполняются Þ П- проективная плоскость.
Определение : Ограниченной конфигурацией называется конфигурация, у которой каждая () принадлежит не менее чем трем прямым, а каждая прямая содержит не менее трех различных точек.
Пример: Конфигурация теоремы Дезарга ограничена.
Предложение 2 : » конечная ограниченная конфигурация из П содержится в p0.
Доказательство: Уровнем () РÎП мы назовем наименьшее n ³0,такое, что РÎpn . Уровнем прямой L ÍП мы назовем наименьшее n ³0, такое, что L Çpn — прямая.
Пусть S — ограниченная конечная конфигурация из П, и пусть n — максимальный из уровней всех точек и всех прямых из S.
Предположим, что n — уровень какой-то прямой L ÍS (Если максимальный уровень достигается для точки, то доказательство аналогично).
Тогда l Çpn — прямая, а l Çpn -1 не является прямой. Если n =0, то все доказано, SÍp0. Предположим, что n >0. Тогда l возникла как прямая, соединяющая две () из pn -1, не принадлежащие в pn -1 одной прямой. Но в S уровень всех точек £n , а значит, они принадлежат pn , то есть l содержит не более двух таких точек. Полученное противоречие и доказывает наше предложение.
Пример: Недезаргова проективная плоскость .
Пусть p0 состоит из четырех точек и не содержит ни одной прямой, П- свободная проективная плоскость порожденная p0.
В качестве следствия из предыдущего предложения получаем, что П бесконечно; следовательно,» прямая содержит бесконечно много точек. Значит можно выбрать четыре () О,А,В,С, » три из которых неколлинеарны, и затем А’на ОА, B’ на ОВ, С’ на ОС так, что они образуют семь различных точек, причем A’,B’,C’ неколлинеарны. Тогда построим Р=АВÇА’В’, Q=ACÇA’C’, R=BCÇB’C’. Все 10 точек различны. Если теорема Дезарга была бы не верна на П, то P ,Q,R принадлежали бы одной прямой, Þ 10 () и 10 прямых образовали бы ограниченную конфигурацию; но тогда она должна была бы содержаться в p0, а p0 содержит всего лишь четыре точки.
Построили геометрию, удовлетворяющую аксиомам П1-П4 и не удовлетворяющую П5, тем самым показали, что П5 не является следствием П1-П4.
3.5. Принцип двойственности
Займемся изучением свойств проективной плоскости, вытекающих из аксиом П1-П4.
Предложение: Пусть П — проективная плоскость, П*- множество прямых плоскости П; назовем еще пучок прямых плоскости П прямой из П*.(здесь П*- это множество элементов из П, называемых прямыми; пучком прямых называется совокупность всех прямых, проходящих через некоторую фиксированную точку- центр пучка). Тогда П* тоже является проективной плоскостью (назовем ее двойственной к П проективной плоскостью); при этом, если П удовлетворяет аксиоме П5, то и П* ей удовлетворяет.
Следствие (принцип двойственности).
Пусть S- некоторое утверждение, касающееся проективной плоскости П, которое может быть выведено из аксиом П1-П4 (соответственно П1-П5). Тогда «двойственное» утверждение S*, полученное из S заменой слов.
лежит на Û проходит через
коллинеарные Û сходящиеся
точка пересечения двух прямых Û прямая, соединяющая две точки
и т.д., тоже может быть выведено из аксиом П1-П4 (соответственно П1-П5).
Определение : Полным четырехугольником называется конфигурация, состоящая из семи точек и шести прямых, полученных следующим образом: рассмотрим четыре точки А,В,С,D (такие, что любые три из них неколлинеарны), шесть соединяющих их прямых и три новые точки пересечения этих прямых.

Точки Р, Q и R называются диагональными точками полного четырехугольника. Диагональные точки P ,Q и R могут оказаться коллинеарными. Однако на действительной проективной плоскости этого быть не может. Мы убедимся в этом позже, пока будем рассматривать случай коллинеарности диагональных точек как исключительное явление и поэтому введем следующую аксиому П7 (аксиома Фано).
П7: Диагональные точки полного четырехугольника неколлинеарны.
Предложение : Действительная проективная плоскость удовлетворяет аксиоме П7.
Определение : Полным четырехсторонником называется конфигурация, состоящая из семи прямых и шести точек, полученных следующим образом: рассмотрим четыре прямые a, b, c, d (такие, что никакие три из них не являются сходящимися), шесть точек их пересечения и три новые прямые p,q,r.
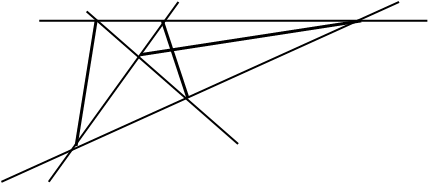 |
Соединяющие пары противоположных вершин полного четырехсторонника прямые p , q, r называются диагоналями полного четырехсторонника.
Предложение : Из того, что П7 выполняется на П Þ, что П7* выполняется на П*; поэтому принцип двойственности применим также и к следствиям из П7.
Докажем П7*: П7* в терминах П означает: диагонали полного четырехсторонника не являются сходящимися (не принадлежат одному пучку). Пусть a, b, c, d- «стороны» полного четырехсторонника; предположим, что диагонали p , g, r- сходящиеся. Но в этом случае диагональные точки полного четырехугольника АВСD, где А=bÇd, B=cÇd, C=aÇb, D=aÇc коллинеарны, что противоречит П7. Значит утверждение П7* справедливо.
Заметим, что определение четырехсторонника двойственно определению полного четырехугольника.
3.6. Гармонические четверки точек.

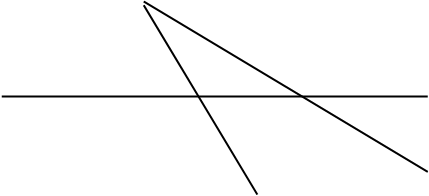 |
Для гармонических точек А,В,С,D мы введем обозначение H (АВ, СD). Из того, что точки А,В,С,D образующие гармоническую четверку, различны, следует неколлинеарность диагональных 
Предложение 1 : Н(АВ,СD)-Н(BA,CD)-H(AB,DC)-H(BA,DC)
Доказательство: Это утверждение немедленно следует из определения гармонической четверки, так как А и В, С и D играют одинаковую роль в построении полного четырехугольника. Действительно, можно переставить буквы X,Y,Z,W,так, чтобы привести обозначение в соответствие с определением Н(ВА,СD) ч.т.д.
Предложение 2 : Пусть А,В,С- три различные точки прямой. Тогда (если выполняется П7) $ точка D, такая, что Н(АВ,СD). Более того (если выполняется П5), можно утверждать, что подобная точка D единственная (D называется четвертой гармонической точкой для А,В,С или точкой, гармонически сопряженной к точке С по отношению к точкам А и В).
Предложение 3 : Пусть А,В,С,D- гармоническая четверка точек. Тогда (если выполняется П5) C,D,A,B- тоже гармоническая четверка.
Объединяя это предложение с предложением 1, получаем:
Доказательство: Пусть Н(АВ,CD) и пусть XYZW- полный четырехугольник, с которым связано определение этой гармонической четверки.
Проведем DX и CZ и обозначим точку пересечения через U. Пусть, далее XWÇYZ=T. Тогда XTUZ- полный четырехугольник, а С и D- две его диагональные точки. Точка ВÎXZ, поэтому достаточно доказать, что TU проходит через А, так как в этом случае будем иметь H(CD,AB). Рассмотрим 2 треугольника XUZ и YTW. Пары их соответственных сторон пересекаются в точках D,B и С, но эти точки коллинеарны Þ по П5*,XY, TU, WZ соединяющие соответственные вершины принадлежат одному пучку.
Пример: На действительной евклидовой плоскости четыре точки А,В,С,D образуют гармоническую четверку тогда и только тогда, когда
3.7. Перспективные и проективные отображения.
Определение : Проективное отображение- это отображение прямой l на l ‘ (быть может, совпадающую с l ), которое, может быть представлено как композиция перспективных отображений.
Обозначение: l – l ’ или АВС…-А’В’С’…
Последняя запись означает, что проективное отображение переводит точки А,В,С,….соответственно в A’,B’,C’,….
Проективное отображение устанавливает взаимно однозначное соответствие между точками прямых l и l ‘ и является отображением на l ‘.
Определение : Перспективным отображением прямой l на прямую l ‘ (обе прямые рассматриваются как множество точек) с центром О (точка О не принадлежит ни l , ни l ‘) называется отображение А®A’, где для произвольной точки АÎl точка А’ находится как ОАÇl ‘.



также является перспективным отображением. Если ()Х=l Çl ‘, то Х (как точка l ) переходит в Х (как точку l ‘). Композиция двух или более перспективных отображений уже не обязательно будет перспективным отображением: так мы имеем l = l ’ = l ’’ и ABCY = A’B’C’Y’ = A’’B’’C’’Y’’ если бы полученное в результате композиции отображений l = l и l = l отображение l на l ‘’ было перспективным, то в точку l Çl ’’=Y оно должно было бы переводить в себя. Однако у переходит в точку Y», которая не совпадает с Y. Поэтому мы ввели проективное отображение.
Предложение 1 : Пусть, задана прямая l . Тогда множество проективных преобразований (взаимно однозначное отображение множества М на себя называется преобразованием множества М). l образует группу. Это означает, что 1)композиция двух проективных отображений снова есть проективное отображение. 2)отображение, обратное проективному отображению, снова есть проективное отображение.
Предложение 2 : Пусть задана прямая l и пусть А,В,С и A’,B’,C’- две тройки ее различных точек. Тогда $ проективное преобразование l , переводящее А,В,С в A’,B’,C’.
Доказательство: Пусть l ‘- прямая отличная от l и не проходящая через А и А’, а О произвольная точка не принадлежащая ни l , ни l ‘. Спроектируем из О точки A’,B’,C’ прямой l в точки A’’,B’’,C’’, прямой l ’: A’B’C’ = A»B»C», где АÏl ’ и А’’Ïl .
Ясно, что нам достаточно построить проективное отображение l на l ’, переводящее A,B,C, в A’’,B’’,C’’.
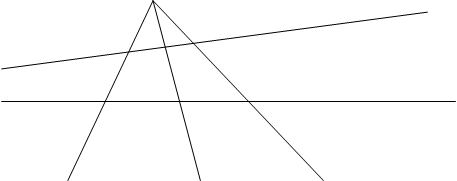 |
Заменим в обозначениях двойные штрихи одинарными и забудем про исходные A’,B’,C’. Таким образом, наша задача свелась к следующей. Заданы две различные прямые l и l ’. Пусть А,В,С- три различные точки l , а A’,B’,C’-три различные точки l ’, предположим что AÏl ’ и A’Ïl . Требуется построить проективное отображение l на l ’, переводящее А,В,С соответственно в A’,B’,C’. Проведем прямые AA’,AB’,AC’,A’B,A’C и положим AB’ÇA’B=B’’, AC’ÇA’C=C’’. Обозначим прямую B’’C’’ через l ’’; пусть она пересекает AA’ в A’’. Тогда l = l ’’ = l ’ переводит ABC = A’’B’’C’’ = A’B’C’.
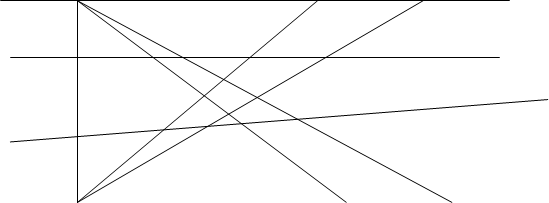 |
Таким образом, мы построили искомое проективное отображение l на l ’ как композиция двух перспективных отображений.
Предложение 3 : Проективное отображение переводит гармоническую четверку точек в гармоническую четверку.
3.8. Аксиома Паппа и основная теорема о проективных преобразованиях прямой.
Докажем “основную теорему”, которая утверждает, что существует единственное проективное преобразование прямой, переводящее три заданные точки в любые другие три заданные точки. Эта теорема не следует из аксиом П1-П5 и П7; поэтому нам предстоит дополнительно ввести аксиому Паппа П6.
Основная теорема (теорема о проективных преобразованиях прямой). Пусть задана прямая l и А,В,С;A’,B’,C’- две тройки различных точек этой прямой. Тогда существует одно и только одно проективное преобразование l , такое, что АВС — A’B’C’.
П6 (аксиома Паппа). Пусть l и l ’-две различные прямые, А,В,С- три различные точки прямой l , отличные от Х=l Çl ’и А’,В’,С’- три различные точки прямой l ’, отличные от Х. Тогда точки P =AB’ÇA’B, Q=AC’ÇA’C, R=BC’ÇB’C коллинеарны.
Предложение 1 : Аксиома П6 влечет за собой двойственную аксиому Паппа П6*, то есть принцип двойственности применим и ко всем выводам из П6.
Предложение 2 : На действительной проективной плоскости справедлива аксиома П6.
Лемма 1 : Пусть l = m = n , где l ¹n , предположим еще, что или:
а)прямые l , m , n принадлежат одному пучку, или
б)точки O,P и l Çn коллинеарны.
Тогда полученное проективное отображение l — n является перспективным (то есть $ такая точка Q, что перспективное отображение l = n совпадает с нашими проективными отображениями l — n ).
Где l ¹n ; предположим теперь, что не имеет места ни а) ни б) из условий леммы 1. Тогда $ прямая m ’ и точки O’În и P’Îl , такие, что l = m = n есть рассматриваемое проективное отображение l на n .
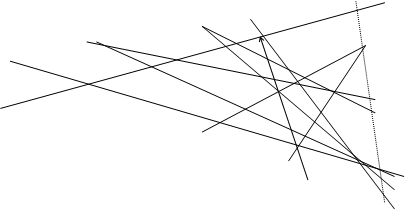 |
Доказательство: Пусть l , m , n , O,P заданы; пусть далее A,A’- две точки на l и AA’ = BB’ = CC’. Точку пересечения ОР и n обозначим через O’. Так как мы предположили, что точки О,Р, l Çn =X неколлинеарны, то O’¹X, то есть O’Ïl . Проведем O’A и O’A’; пусть они пересекаются РС и РС’ соответственно в D и D’.
Соответствующие стороны треугольников АBD и A’B’D’ пересекаются в коллинеарных точках O,P ,O’; значит, по П5*, прямые, соединяющие соответственные вершины этих треугольников принадлежат одному пучку. Таким образом, прямая m 1, содержащая D и D’, проходит через точку Y=l Çm .
Следовательно, прямая m 1 определена точками D и Y, и если точка A’ меняется, то D’ меняется, оставаясь на прямой m 1. Поэтому исходное проективное отображение совпадает с отображением l = m 1 = n .
Повторяя то же самое рассуждение еще раз, мы можем переместить Р в положение P ’=OP Çl и найти новую прямую m ’, такую, что l = m ’= n дает исходное проективное отображение.
Лемма 3 : Пусть l и l ’- две различные прямые. Тогда любое проективное отображение l — l ’ может быть получено как композиция двух перспективных отображений.
Теорема 1 : Основная теорема вытекает из аксиом П1-П6.
Доказательство: Для заданной прямой l и двух троек различных точек А,В,С и A’,B’,C’ этой прямой мы должны найти проективное преобразование, переводящее одну тройку в другую, и доказать, что оно единственно. Выбираем прямую l ’, не проходящую через заданные точки, и спроектируем A’,B’,C’ на l ’. Обозначим образы этих точек теми же буквами A’,B’,C’. Таким образом мы свели теорему к следующей: имеем А,В,С на l A’,B’,C’ на l ’ (все точки отличны от l Çl ’) требуется показать, что $ единственное проективное отображение, такое, что ABC — A’B’C’. Одно такое проективное отображение мы уже получили в предложении 2 (п.3.7); следовательно, достаточно показать, что любое другое проективное отображение совпадает с этим.
Случай 1 : Предположим, что второе проективное отображение есть просто перспективное отображение. Пусть l — l ’ переводит ABC = A’B’C’. Рассмотрим P =AB’ÇA’B ; пусть прямая l ’’ соединяет Р с Q. Мы утверждаем, что l ’’ проходит через точку Х=l Çl ’. Действительно, применим П5 к треугольникам AB’C’ и A’BC, которые перспективны с центром О. Их стороны пересекаются в точках Р,Q,Х соответственно. Следовательно, l ’’ определяется точками Р и Х.
 |
Но так как С может меняться, перспективное отображение l = l ’ совпадает с проективным отображением l = l ’’ = l ’
Случай 2 : предположим, что второе проективное отображение не является перспективным. Тогда в силу леммы 3 оно может быть представлено в виде композиции двух перспективных отображений, а в силу леммы 2 можно предположить, что центры этих отображений принадлежат соответственно l ’ и l . Таким образом, мы приходим к конфигурации: l = l ’’ = l ’ и ABC = A’’B’’C’’ = A’B’C’
 | |
 |
Применяя П6 к треугольникам АBR и A’B’R’, мы получаем, что Р=АB’ÇA’BÎl ’’. Аналогично, применяя П6 к ACR и A’C’R’, мы получаем, что Q=AC’ÇA’CÎl ’’. Таким образом, l ’’ есть прямая, которая была использована в предложении 2 (п.3.7) для построения второго проективного отображения
Пусть теперь DÎl – произвольная точка; определим D’’=R’DÇl ’’и D’=RD’’Çl ’.
Из П6, применимой к треугольникам ADR и A’D’R’, следует, что AD’ÇA’D, A’’,D’’ коллинеарны, то есть AD’ÇA’DÎl ’’. Но это означает, что также и проективное отображение предложения 2 переводит D в D’. Следовательно, эти проективные отображений совпадают. ч.т.д.
Теорема 2: П5 следует из П6.
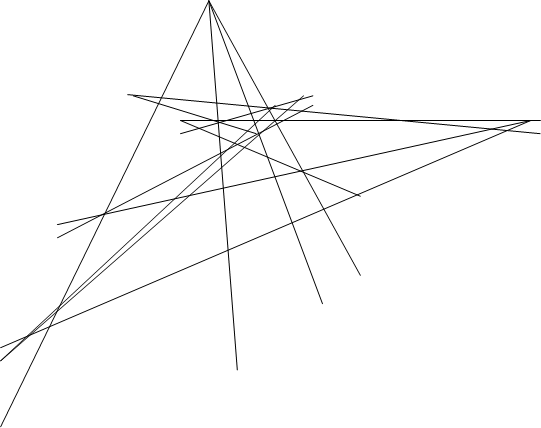
Доказательство: Пусть, О,A,B,C,A’,B’,C’ удовлетворяют предложениям теоремы Дезарга (П5), построим P ,Q,R. Для доказательства их коллинеарности нам придется трижды применить П6.
Шаг 1: Пусть A’C’ пересекает АВ в точке S. Затем применим П6 к прямым.

BSA и заключим отсюда, что точки T=OSÇBC, U=OAÇBC’, Q коллинеарны.
и заключим отсюда, что точки U,V=OSÇB’C’, P коллинеарны.
и заключим отсюда, что точки R, P =BSÇUV (шаг2),Q=C’SÇTU (шаг1) коллинеарны. ч.т.д.
 |
Следствие : (из основной теоремы). Проективное отображение l — l ’, где l ¹l ’, есть перспективное отображение Û точка пересечения X=l Çl ’ переходит в себя.
Глава 4. Применение основных теорем к решению задач на евклидовой плоскости.
4.1. Использование теоремы Дезарга на евклидовой плоскости.
В аксиоматическом построении проективной плоскости мы рассматриваем теорему Дезарга, как аксиому. Покажем, что она справедлива на евклидовой плоскости. Если две одинаковые конфигурации, составленные из точек и прямых, могут быть приведены в соответствие так, что пары соответствующих точек соединяются прямыми, пересекающимися в одной точке, то мы говорим, что эти две конфигурации перспективны относительно этой точке. Если соответствие таково, что пара соответствующих прямых пересекаются в точках лежащих на одной прямой, то говорим, что эти две конфигурации перспективны относительно этой прямой.
Сформулируем теорему Дезарга, покажем использование на евклидовой плоскости.
При доказательстве будем пользоваться теоремой Менелая.
Теорема Менелая гласит:
Если точки X,Y,Z лежащие на сторонах ВС,СА,АВ (соответственно продолженных) треугольника АВС коллинеарны, то (BX/CX)*(CY/AY)*(AZ/BZ)=1
Обратно, если это уравнение выполняется для точек X,Y,Z, лежащих на трех сторонах треугольника, то эти три точки коллинеарны.
 |
 |

 |
Если два треугольника перспективны относительно точки и если их пары соответствующих сторон пересекаются, то эти три () пересечения коллинеарны.
Доказательство: Мы имеем теорему лишь о принадлежности () прямым и пересечении прямых. Треугольники АВС и A’B’C’ перспективны относительно точки О, а пары их соответствующих сторон пересекаются в () R,Q,P. Для доказательства применим теорему Менелая к тройкам точек.
Лежащих на сторонах трех треугольников ОАС, ОСВ, ОВА, получим при этом (AQ/CQ)*(CC’/OC’)*(OA’/AA’)=1 (CR/BR)*(BB’/OB’)*(OC’/CC’)=1
Перемножим эти три выражения и проделав умеренное число сокращений, получим (AQ/CQ)*(CR/BR)*(BP/AP)=1Þ что () Q,R,P коллинеарны, теорема доказана.
4.2. Использование предложения Паппа на евклидовой плоскости.
Покажем использование предложения на евклидовой плоскости.
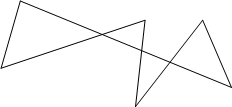
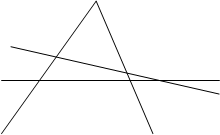
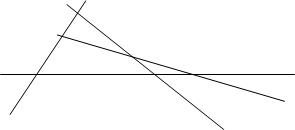
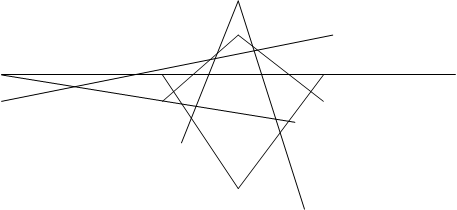
Теорема Паппа : Если А,С,В — три точки на одной прямой, а A’,C’,B’ — на другой, и если три прямые AB’,CA’,BC’ пересекают прямые A’B,C’A,B’C соответственно, то три точки пересечения P,Q,R коллинеарны.
 | ||
 | ||
Доказательство: Эта теорема как и теорема Дезарга использует принадлежность точек прямым или прохождение прямых через точки, без измерения длин или углов и даже без какой-либо ссылки на порядок; в каждом множестве из трех коллинеарных точек безразлично, какая из них лежит между двумя другими. (рис. 1, рис. 2)
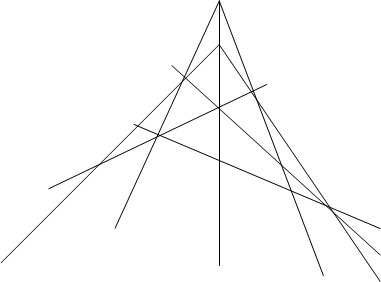 |
 |
 |
Применяя теорему Менелая к пяти тройкам точек
íP,A’,Bý, íA,Q,C’ý, íB’,C,Rý, íA,C,Вý, íB’,A’,C’ý,
лежащих на сторонах этого треугольника, мы получаем.
Разделив произведение первых трех соотношений на произведение последних двух, производя сокращение, мы получаем:
то есть P,Q,R коллинеарны, теорема доказана.
№1 . Если два треугольника перспективны относительно точки и две пары соответствующих сторон параллельны, то и две оставшиеся стороны параллельны.

Доказать что: QP||Q’P’

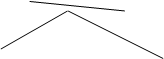 | |
 |
№2 .Назовите два треугольника перспективных относительно:
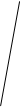


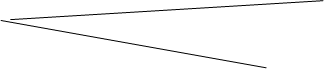 |
Ответы: а) треугольники ROQ и EP’F б) треугольники EFP и R’Q’O’ в) треугольники R’RE и Q’QF.

 |
1) АС||BD. Рассмотрим параллелограмм ABDE и AFDCÞBD=AE и DF=AC. Произведем вычитание BD-DF=BF; AE-AC=CEÞBF=CEÞBCEF — параллелограмм ÞEF||BC.
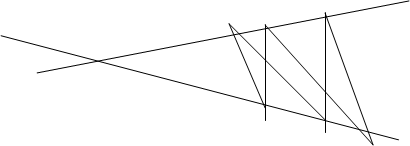 |
3) ACÇBD=0, так как AB||ED и CD||FA, то (|OA|/|OB|)=(|OE|/|OD|) и (|OC|/|OD|)=(|OA|/|OF|) получаем |OB|*|OE|=|OA|*|OD|=|OC|*|OF| Þ
№4. Пусть A,B,D,E,N,M — шесть точек, обладающих тем свойством, что прямые AE,DM,NB пересекаются в одной точке и прямые АМ,DB,NE пересекаются в одной точке. Что можно сказать о прямых AB,DE,NM?
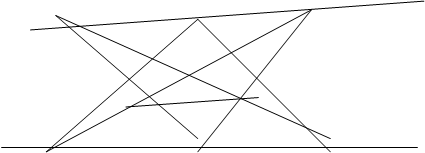 |
Решение. Пусть AEÇDMÇNB=C, AMÇDBÇNE=F обозначим () пересечения прямых АВ и DE через L. По теореме Паппа ()LÎMNÞABÇDEÇMN=L. Прямые AB,DE,NM пересекаются в одной точке.
№5. Доказать, что медианы треугольника пересекаются в одной точке.
Решение: Рассмотрим треугольник АВС и треугольник А1В1С1- дезарговые треугольники, то есть треугольники удовлетворяют теореме Дезарга.
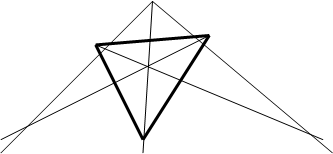 |
 |
 |
лежат на одной несобственной прямой S¥
по обратной теореме Дезарга прямые, проходящие через соответствующие вершины, пересекаются в одной точке S.

 |
Решение: треугольники NCK и AMP дезарговые треугольники по прямой теореме Дезарга, соответствующие стороны этих треугольников пересекаются в ()-ах, лежащих на одной прямой Þ ()F,D,B, то есть () пересечения непараллельных сторон трапеции принадлежат диагонали BD.
№7. В евклидовой плоскости противоположные вершины одного параллелограмма расположены соответственно на противоположных сторонах второго. Доказать, что оба параллелограмма имеют общий центр симметрии.

 |
ACÇLNÇBD — треугольники ALD и СNB — дезарговые треугольники удовлетворяют обратной теореме Дезарга ÞACÇLNÇBD=S.
Треугольники DKC и BMA — дезарговые треугольники по обратной теореме Дезарга ÞMKÇBDÇAC=S
Оба параллелограмма имеют общий центр симметрии.
№8. В евклидовой плоскости дан треугольник и три параллелограмма, для каждого из которых одна сторона треугольника служит диагональю, а две другие — смежными сторонами. Доказать, что вторые диагонали этих параллелограммов пересекаются в одной точке.
Требуется доказать, что ANÇBPÇCM=S.

 |
 |

лежат на одной несобственной прямой P¥
по теореме обратной теореме Дезарга NAÇBPÇCM=S.
№9. В треугольнике АВС из его вершин проведены прямые, пересекающиеся в одной () S; A’=ASÇBC, B’=BSÇAC, C’=CSÇAB. Доказать, что точки BCÇB’C’, ACÇA’C’, ABÇA’B’ лежат на одной прямой.

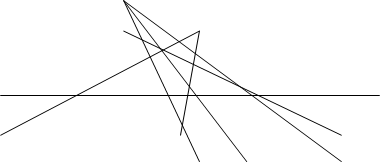 |
Обозначим () пересечения сторон BCÇB’C’, ACÇA’C’, ABÇA’B’ соответственно P,R,Q. Рассмотрим треугольники АВС и А’В’С’ прямые проходящие через вершины этих треугольников пересекаются в () SÞ () пересечения соответствующих сторон P,R,Q лежат на одной прямой.
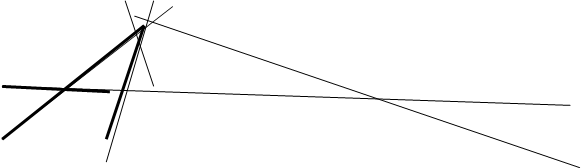 |
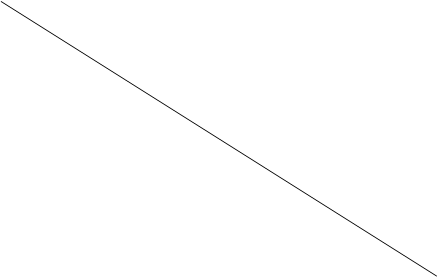
Точка А- дезаргова точка
Треугольники A’RP и SCB — дезарговы треугольники
Точки C’,B’,QÎS — дезаргова прямая.
№11. Сформулировать в терминах евклидовой геометрии теорему Дезарга для случая:
1) ()S¥ — несобственная (), дезаргова прямая S — собственная.
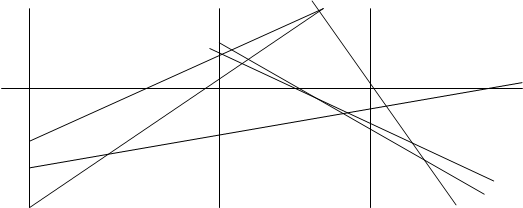 |
Формулировка теоремы Дезарга: Если прямые проходящие через соответствующие вершины двух треугольников параллельны, то точки пересечения соответствующих сторон лежат на одной прямой.
2) ()S собственная, прямая S¥ — несобственная.
 |
 |
 |
3) ()S¥ — несобственная, прямая S¥ — несобственная.
Если прямые проходящие через соответствующие вершины двух треугольников параллельны и AB||A’B’, BC||B’C’, то AC||A’C’.
№12. Прямая p лежит в плоскости треугольника АВС; К=ВСÇp, L=ACÇp, M=ABÇp, R=BLÇCM, S=CMÇAK, T=AKÇBL.

Требуется доказать, что ARÇBSÇCT=Q
 |
TSÇBC=K () M,K,LÎз (по условию)
Таким образом, по теореме обратной теореме Дезарга ARÇBSÇCT=Q.


 |
Выбираем произвольно прямую s, () A,A’Îa и ()ВÎb.
1)ABÇs=P, 2)PA’Çb=B’, 3)ACÇs=R,
4)BCÇs=Q, 5)A’R, B’Q, 6)B’QÇA’R=C’,
7)CC’ искомая прямая.
ACÇA’C’=RÎs (по построению)
По обратной теореме Дезарга AA’ÇCC’ÇBB’=S.
№14. Даны две точки P и Q и не проходящая через них прямая c. построить () PQÇC, не проводя PQ.
Анализ: Произвольно выбираем прямую s, ()Q1ÎC,Q


1) 
2) 
5) 
7) P2 Q2 Çc=S ()S — искомая точка.
По обратной теореме Дезарга. PQÇP1 Q1 ÇP2 Q2 =SÞPQÇc=S искомая точка.
№15. На евклидовой плоскости даны две параллельные прямые a||b и точка С, им не принадлежащая. Через () С провести прямую, параллельную а и b.
1) Анализ: Произвольно выбираем прямую s. ()А,А’Îа, ()ВÎb.
Здесь работает обратная теорема Дезарга для случая ()S¥ — несобственная, прямая s — собственная.
Треугольники АВС и А’В’С’ — построить.
|
|
|
|
|
|
|
|
|

|
|
6) A’RÇB’Q=C’
7) CC’ — искомая прямая.
|
3) Доказательство:
Треугольники АВС и А’В’С’- дезарговы
Формулировка обратной теоремы Дезарга.
Если прямые, содержащие соответственные стороны треугольников АВС и А’В’С’ пересекаются в точках лежащих на одной прямой и АА’||BB’, то СС’||AA’.
По этой теореме СС’- искомая прямая.
№18. Трапеция ABCD пересечена прямыми p и q, параллельными основанию АВ, pÇAD=M, pÇAC=P, qÇBD=N, qÇBC=Q. Доказать, что точка MNÇPQ лежит на прямой АВ.
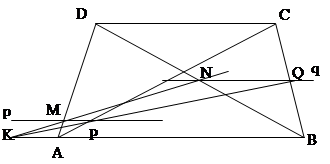
DC||p||qÞDCÇpÇq=S¥ ÞC,D,S¥ Î одной прямой по теореме обратной теореме Дезарга MNÇPQÇAB=K.
Тем самым доказали, что точка МNÇPQÎAB.
№17. В евклидовой плоскости даны параллелограмм АВСD, ()РÎCD и прямая l пересекающая стороны АВ и АD. Провести прямую || l .
1) 
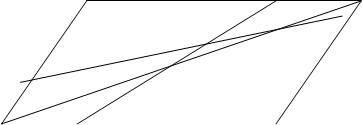 |
1) 
2) 
4) KP- искомая прямая.
треугольники ANM и CPK — дезарговы, так как ANÇCP=R¥ (AN||CP), CKÇAM=Q¥ (CK||AM) то по теореме Дезарга KPÇNM=F¥ ÞKP||NM.
1. Р. Хартсхорн “Основы проективной геометрии”.-М:Мир,1970.
2. Ефимов “Высшая геометрия”-:Наука,1971.
3. Франгулов С.А. “Лекции по проективной геометрии”-Л:ЛГПИ,1975.
4. Вахмянина О.А., Измайлова Т.С. “Пособие по проективной геометрии”-Оренбург:ОГПИ,1994.
5. Коксетер С.М. “Новые встречи с геометрией”-М:Нуака,1978
6. Базылев “Геометрия”-М:Просвещение,1975
7. Потоцкий “Что изучает проективная геометрия ”-М: Просвещение,1982
8. Певзнер “Проективная геометрия”-М:Просвещение,1980
9. Измайлова Т.С. Лекционный курс по проективной геометрии.
Методическое пособие «Проективная геометрия» для студентов-математиков
ФГАОУ ВО «КРЫМСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ имени В.И. Вернадского» ГУМАНИТАРНО-ПЕДАГОГИЧЕСКАЯ АКАДЕМИЯ (ФИЛИАЛ) В Г. ЯЛТЕ
ИНСТИТУТ ЭКОНОМИКИ И УПРАВЛЕНИЯ
для студентов-бакалавров специальности «Математика»
Рекомендовано ученым совета Гуманитарно-педагогической академии (филиал) «Крымский федеральный университет им. В.И. Вернадского» от «8» декабря 2015 года (протокол № 11)
Б 90 Проективная геометрия. / Бубнова А.А.:
Методическое пособие. – Ялта: РИО ГПА, 2016. – 84с.
Данное пособие предназначено для студентов математических и экономических специальностей, для учащихся старших классов, учителей школ и преподавателей вузов. Пособие содержит программный материал по проективной геометрии. Может быть использовано для подготовки к экзамену по геометрии и высшей математике.
Орлов В.Н., доктор физико-математических наук, профессор кафедры математики, теории и методики обучения математике Гуманитарно-педагогической академии (филиал) в г. Ялте «Крымского федерального университета им. В.И. Вернадского».
Овчинникова М.В., кандидат педагогических наук, доцент кафедры математики, теории и методики обучения математике Гуманитарно-педагогической академии (филиал) в г. Ялте «Крымского федерального университета им. В.И. Вернадского».
© Бубнова А.А., 2016 г.
© Гуманитарно-педагогическая академия (г. Ялта), 2016 г.
Вступление
Дисциплина проективная геометрия является одной из базовых дисциплин высшей математики. Предметом проективной геометрии является изучение свойств геометрических фигур, которые сохраняются при центральном проецировании.
Понятие проективного пространства введено путем расширения евклидового пространства – дополнением его несобственными точками, несобственными прямыми и несобственной плоскостью. Построенное таким образом проективное пространство имеет все свойства, необходимые для объяснения проективных понятий. Кроме того, такой подход к построению проективного пространства дает возможность тесно связать новые понятия и теоремы проективной геометрии с соответствующим материалом евклидовой геометрии, что облегчает пониманию студентами новых проективных понятий.
Настоящее пособие призвано помочь студентам освоить фундаментальные факты проективной геометрии геометрии. Основная цель – научить студентов решать задачи. В связи с этим много примеров дано с подробным объяснением.
В пособии приведены основные теоретические сведения, которые необходимы для выполнения заданий. По каждой теме приведены примеры решения задач.
Пособие содержит две контрольных работы: по проективной геометрии и по начертательной геометрии. В приложении указаны темы рефератов и вопросы для экзамена, предложены решения контрольных работ.
1 ПРОЕКТИВНАЯ ГЕОМЕТРИЯ
1.1.Построение проективного пространства
1.1.1.Центральное проецирование в евклидовом пространстве;
Проективная геометрия изучает свойства геометрических фигур, которые не изменяются при каком-нибудь центральном проецировании. Поэтому необходимо изучить свойства такого проецирования.
Центральное проецирование в пространстве
Пусть заданы две плоскости 






Точка S называется центром проецирования, точка 


Если в плоскости 





Точка D прямой АВ отображается в точку 

Если в плоскости 



Центральное проецирование на плоскости
Аналогично можно установить проективное соответствие между точками двух прямых на плоскости. Пусть имеем две прямые а и 






— это центральная проекция точки В прямой а, а прямая 
Из способа установления проективного отношения следует, что центральной проекцией точки есть точка, если она существует; проекцией прямой , что не проходит через центр проецирования, есть прямая; точки, которые лежат на одной прямой, отображаются на точки, которые лежат на соответствующей прямой; прямые, которые проходят через одну точку (пучок прямых), переходят в прямые, которые проходят через одну точку, таким образом инцидентность точек и прямых при центральном проектировании не нарушается.
Но не для каждой точки прямой а есть образ на прямой 






Пусть в пространстве между плоскостями 




Тогда никакой точке М прямой а пересечения плоскостей 







Аналогично, ни какая точка 







Таким образом, если взять фигуру F в плоскости 


Итак, проективное отображение в евклидовом пространстве не взаимно однозначно.
Пример 1.Дан треугольник АВС в плоскости 



Решение. Центральной проекцией точки В будет точка 


Поскольку проектирующий луч SA параллелен плоскости 


1.1.2. Построение проективного пространства;
1. Проективная прямая
Наличие значительных недостатков отношения, которое устанавливается центральным проектированием в евклидовом пространстве, не дают возможности использовать метод центрального проектирования в полном объеме для изучения свойств фигур, которые не меняются при этом проектировании. Поэтому для изучения проективных свойств фигур евклидовое пространство необходимо дополнить некоторыми объектами так, чтобы в новом дополненном пространстве перспективное отображение было взаимно однозначным.
Впервые такое дополнение осуществил французский математик и архитектор Ж.Дезарг (1591-1661), который ввел понятие бесконечно удаленной точки и прямой.
Чтобы перспективное соответствие между точками двух прямых (смотри рис.2) стало взаимно однозначным, необходимо, чтобы прямая SC , параллельная прямой 



Аналогично, прямую а дополняют бесконечно удаленной точкой 

Определение 1. Несобственной точкой называют общую точку параллельных двух прямых.
Итак, пучок параллельных прямых имеет одну общую несобственную точку (рис. 5).
Определение 2. Евклидова прямая, дополненная несобственной точкой, называется проективной прямой.
Введем понятие несобственной прямой.
На евклидовой плоскости можно провести бесконечно много прямых разных направлений через какую-нибудь точку плоскости. Каждую из этих прямых дополняем несобственной точкой, их будет бесконечно много. Пусть на плоскости 

Чтобы провести луч до несобственной точки 














Итак, геометрическое место образов 





Определение 3. Несобственной прямой плоскости называется множество всех несобственных точек данной плоскости.
Следствие. Параллельные плоскости пересекаются по несобственной прямой. Пучок параллельных плоскостей имеет одну общую несобственную прямую.
Определение 4. Евклидова плоскость, дополненная несобственной прямой, называется проективной плоскостью.
Определение 5. Множество всех несобственных точек и всех несобственных прямых называется несобственной плоскостью.
Каждая собственная прямая с несобственной плоскостью имеет одну общую точку — несобственную точку прямой. Каждая собственная плоскость имеет с несобственной плоскостью одну общую прямую – несобственную прямую плоскости. Других несобственных точек, не принадлежащих несобственной плоскости, в пространстве не существует.
Определение 6. Евклидово пространство, дополненное несобственными точками, несобственными прямыми и несобственной плоскостью, называется проективным пространством.
Построение проективного пространства с помощью дополнения евклидового пространства несобственными элементами есть одна из моделей проективного пространства. Эту модель еще называют основной моделью проективного пространства.
Несобственные элементы пространства определяют с помощью собственных элементов, а именно:
1)несобственная точка 
2)несобственная прямая 

Задача 1. Даны две несобственные точки 

Решение. Плоскость однозначно определяется тремя точками, которые не лежат на одной прямой. Несобственные точки 
Чтобы построить плоскость, проведем через точку С прямую 


1.1.3. Аксиомы принадлежности проективного пространства;
1.Основные объекты и отношения проективной геометрии
Основными объектами проективной геометрии есть точки, проективные прямые и проективные плоскости проективного пространства.
Основными отношениями между основными объектами есть отношение принадлежности, отношение порядка и отношение непрерывности.
Поскольку в проективной геометрии не сохраняются метрические свойства фигур, а также отсутствует понятие параллельности, то отсутствуют соответствующие группы аксиом.
Система аксиом проективной геометрии складывается из трех групп:
1) принадлежности; 2) порядка; 3) непрерывности.
Проективная прямая и проективная плоскость отличаются от соответствующих понятий евклидовой геометрии наличием несобственных элементов, поэтому формулировки аксиом, которые лежат в основе проективной геометрии, отличаются от аксиом евклидовой геометрии большей общностью.
2. Аксиомы принадлежности проективной геометрии
В аксиомах принадлежности называются три основных отношения, которые связывают точки, прямые и плоскости: принадлежность точки прямой, принадлежность точки плоскости, принадлежность прямой плоскости.
В аксиомах 1.1-1.8 евклидовой геометрии идет речь лишь о тех свойствах точек, прямых и плоскостей, которые являются инвариантами центрального проектирования.
Но аксиомы принадлежности проективной геометрии удобней дать по другому, более общую формулировку.
1 группа. Аксиомы принадлежности
Н.1. Две различные точки А и В всегда принадлежат одной и только одной прямой.
Н.2. Две различные плоскости 
Н.3. Точка А и прямая а, которая ей не принадлежит, всегда принадлежат одной и только одной плоскости.
Н.4. Плоскость 
Н.5. Существует, по крайней мере, четыре точки, которые не принадлежат как одной прямой, так и одной плоскости.
Н.6. Если точка А принадлежит прямой а, а прямая а принадлежит плоскости 

Сформулированные аксиомы принадлежности справедливы как для собственных, так и для несобственных объектов, так что имеют большее значение, чем соответствующие аксиомы евклидовой геометрии.
Следствия из аксиом принадлежности
1.Три различные точки А, В и С, которые не принадлежат одной прямой, принадлежат одной и только одной плоскости.
По аксиоме Н.1 существует прямая АВ, которой принадлежат точки А и В. Так как точка С не принадлежит прямой АВ, то по аксиоме Н.3 прямая АВ и точка С определяют одну и только одну плоскость, которой принадлежат точки А, В, С.
2. Три различные плоскости 
Справедливость этого утверждения выходит из того, что по аксиоме Н.2 существует прямая а, которая принадлежит плоскостям 



3.Если две точки прямой принадлежат плоскости, то и все другие точки прямой принадлежат этой плоскости.
Это следствие докажем методом от противного. По условию две точки А и В принадлежат плоскости 


4.Если две плоскости принадлежат одной точке, то и их общая прямая принадлежит этой точке.
Пусть А – общая точка двух плоскостей 
5.Существует четыре плоскости, которые не принадлежат одной прямой и не принадлежат одной точке.
Справедливость этого утверждения выходит из того, что по аксиоме Н.5 существуют четыре точки, которые не принадлежат как одной прямой, так и одной плоскости. Ни одна из троек не принадлежит одной прямой, так как в противном случае, с последней четвертой точкой эта прямая определяла бы плоскость, которой принадлежали бы все четыре точки.
Существует много других следствий из аксиом принадлежности проективного пространства, на которых мы остановимся дальше. Аксиомы принадлежности и их следствия используются для решения задач, доказательства теорем.
Задача 1. Даны две несобственные точки 

Решение. Плоскость однозначно определяется тремя точками, которые не лежат на одной прямой. Несобственные точки 
Чтобы построить плоскость, проведем через точку С прямую 


1.1.4 Аксиомы порядка проективного пространства;
Отношение порядка точек на проективной прямой
Отношение порядка точек на проективной прямой определяется свойствами проективной прямой, которые значительно отличаются от свойств евклидовой прямой.
Проективная прямая есть замкнутая линия.
Это свойство можно объяснить следующими пояснениями. Пусть имеем прямую s и точку S , которая не лежит на прямой s . Возьмем точку S за центр пучка прямых S ( a , b , c , …) и установим соответствие между прямыми пучка S и точками прямой s , считая образом прямой точку пересечений этой прямой с прямой s . Такое соответс т вие между прямыми пучка S и точками прямой s наз ы вается перспективним соответствием.
Например, точка А прямой s соответствует прямой SA и наоборот. Поскольку проективная прямая – это евклидова прямая, дополненная несобственной точкой, перспективное соответствие между пучком прямых S ( a , b , c , …) и точками прямой s будет взаимно однозначным. Луч n пучка S , параллельный прямой s , соответствует несобственной точке прямой s — 
Все прямые пучка получим поворотом одной из прямых пучка на 



Аналогично, поворачивая луч SA по часовой стрелке, достигаем положение луча 

2. Проективная прямая двумя своими точками разбивается на два отрезка.
Известно, что евклидова прямая двумя своими точками разбивается на три части: отрезок и два луча. Поскольку проективная прямая – это замкнутая линия, то какая-нибудь точка не разбивает ее на части, а лишь разрезает, размыкает. На проективной прямой собственная и несобственная точки равноправны, поэтому отрезки АВ и 
Понятие «отрезок прямой» есть инвариант центрального проектирования, то есть проективным понятием.
Рассмотри дальше расположение точек на проективной прямой. Известно, что в евклидовой геометрии принадлежность точек отрезку устанавливается отношением «лежать между».
При перспективном отображении это отношение ни есть инвариантом, поэтому не рассматривается в проективной геометрии.
Основным отношением, на котором основывается отношение порядка точек проективной прямой, есть разделяемость двух пар разных точек прямой. На рис. 8 пара точек (А,В) прямой s разделяется парой точек (С,Д).
При центральном проектировании прямой s на прямую 









4. Разделяемость ( или неразделяемость ) двух пар точек одной прямой есть инвариант при каком-нибудь проективном отображении этой прямой на другую прямую.
Аксиомы порядка проективной геометрии
В аксиомах порядка устанавливаются свойства разделяемости ( неразделяемости ) двух пар точек проективной прямой. Группу аксиом порядка сформулируем такими утверждениями.
П.1. Две разные точки А и В прямой разбивают все другие точки этой же прямой на два класса.
Определение 7. Каждый из классов, дополненных точками А и В, называется отрезком.
Определение 8. Если точки С и D принадлежат разным классам относительно точек А и В, то пары точек (А,В) и (С, D ) называются разделяемыми. Пишут 
Если точки С и D принадлежат одному классу, то пары точек (А, В) и (С, D ) называются неразделяемыми. Пишут: (А, В) 
П.2. Если (А, В) 

П.3. Какие-нибудь четыре точки прямой можно только одним способом разбить на пары разделяемых.
П.4. Центральное проецирование переводит две разделяемых пары в две разделяемые пары.
Задача 2. Даны пять точек проективной прямой А, В, С, D , E . С помощью аксиом порядка доказать, что если пара (А, В) разделяет пару (С, D ) и пара (А, В) не разделяет пару ( D , E ), то пара (А, В) разделяет пару (С, Е).
Решение. По условию задачи пара точек (А, В) 






Свойства отношения порядка на проективной плоскости
Какая-нибудь прямая а проективной плоскости не разбивает ее на две области.
Две прямые проективной плоскости разбивают ее на две области.
Три прямые проективной плоскости разбивают ее на четыре области, (рис. 10).
Проективная плоскость является замкнутой и односторонней.
1.1.5. Аксиома непрерывности проективного пространства.
Отношение непрерывности проективного пространства
Аксиом первых групп – принадлежности и порядка не достаточно для изучения всех свойств проективного пространства, их необходимо дополнить аксиомой непрерывности, поскольку отношение непрерывности не вытекает из аксиом принадлежности и порядка. Такой аксиомой может быть проективная форма аксиомы Дедекинда (1831-1916).
Д.1. Пусть все точки отрезка АВ разбиты на два класса, причем точка А принадлежит первому, а точка В – второму классу. Обозначим через М произвольную точку первого класса, отличную от точки А, а через N – точку второго класса, отличную от В. Если для какой-нибудь пары точек М и N справедливо условие 

На основе сформулированных аксиом трех групп – принадлежности, порядка и непрерывности – можно самостоятельно построить проективное пространство и изучать его свойства.
1.2. Основные геометрические формы. Теорема Дезарга
1.2.1. Основные геометрические формы;
1. Основные геометрические формы
Основные геометрические формы проективной геометрии формируются по ступеням. К одной форме принадлежат те формы, между которыми можно установить взаимно однозначное соответствие.
Формы первой ступени
1.Прямолинейный ряд точек — это множество всех точек, которые принадлежат одной прямой, называется носителем ряда, и обозначают s ( A , B , C , D , …), где s – дання прямая, А, В, С, … — точки на ней, (рис.11).
2.. Пучок прямих – это множество всех прямых данной плоскости, которые принадлежат данной точке, которая называется носителем или центром пучка, обозначают S ( a , b , c , d ,…), (рис.12).
3.Пучок плоскостей – это множество всех плоскостей, которые принадлежат одной прямой, которая называется носителем пучка, или осью, обозначают 
Формы второй ступени
Плоское поле точек – это множество всех точек данной плоскости, которая называется носителем. Обозначается
Плоское поле прямых – это множество всех прямых данной плоскости, которая называется носителем этого поля. Обозначается 
Связка прямых – это множество всех прямых пространства, которые принадлежат данной точке, которая называется носителем, или центром связки.
Связка плоскостей – это множество всех плоскостей, которые принадлежат данной точке, которая называется носителем, или центром связки.
Формы третьей ступени
1.Пространство точек – это множество всех точек проективного пространства, которое играет роль носителя точек.
2.Пространство плоскостей – это множество всех плоскостей проективного пространства, которое является носителем плоскостей.
Одна из основных теорем проективной геометрии названа именем Ж . Дезарга (1591-1661) – французского математика и архитектора, основоположника проективной и начертательной геометрии.
Теорема Дезарга. Если три прямые, которым принадлежат соответствующие вершины двух данных треугольников, принадлежат одной точке, то три точки, принадлежащие парам соответствующих сторон этих треугольников, принадлежат одной прямой.
Доказательство теорема рассмотрим для двух случаев.
1.Пусть два данных треугольника АВС и 


Можно считать, что треугольник 
Прям ые 












Теорема, обратная теореме Дезарга. Если три точки, которые принадлежат соответствующим сторонам двух данных треугольников, принадлежат одной прямой, то три прямые, принадлежащие парам соответствующих вершин этих треугольников, принадлежат одной точке.
Доказательство. Пары соответствующих сторон данных треугольников АВС и 








Даны треугольники 
Прямые 















При проектировании с точкой 





1.2.2. Принцип двойственности в проективной геометрии;
Анализируя формулировки аксиом принадлежности, основных геометрических форм проективного пространства и следствия из них, легко заметить симметричность выражений относительно слов «точка» и «плоскость». Например, аксиому Н.2 получаем из аксиомы Н.1, заменив слово «точка» словом «плоскость». Аналогично, получаем аксиому Н.4 из аксиомы Н.3, при этом в обоих случаях слово «прямая» осталось без изменений. Такая же симметрия существует в определениях основных форм проективного пространства. Например, прямолинейный ряд точек – это множество всех точек, которые принадлежат одной прямой. Заменив слово «точка» на слово «плоскость», получим определение пучка плоскостей как множество всех плоскостей, который принадлежат одной прямой.
Этот факт в проективной геометрии известен под названием принципа двойственности в пространстве, который формулируется так.
Если в каком-нибудь истинном утверждении про принадлежность основных элементов проективного пространства (точек, прямых, плоскостей) всюду слово «точка» заменить словом «плоскость» и слово «плоскость» — словом «точка», а слово «прямая» оставить без изменений, то получим также истинное утверждение в проективном пространстве.
Принцип двойственности в пространстве еще называют большим принципом двойственности. Принцип двойственности имеет место и на плоскости. Его называют малым принципом двойственности на плоскости.
Если в каком-либо истинном утверждении про принадлежность основных элементов проективной плоскости (точек и прямых) всюду слово «точка» заменить словом «прямая», слово «прямая» — словом «точка», то получим истинное утверждение на проективной плоскости.
http://www.bestreferat.ru/referat-95563.html
http://infourok.ru/metodicheskoe-posobie-proektivnaya-geometriya-dlya-studentovmatematikov-1230003.html

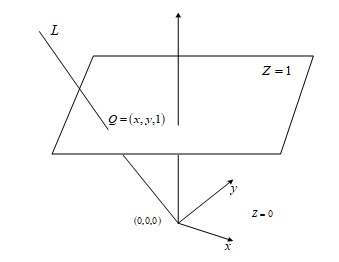

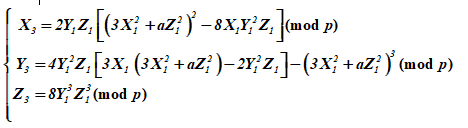
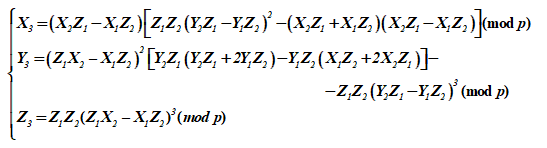
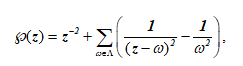
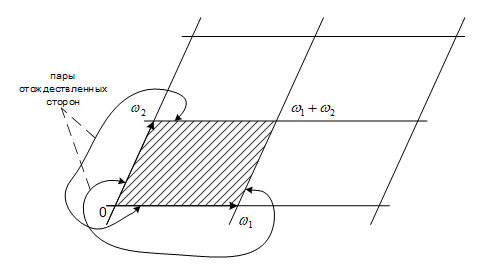
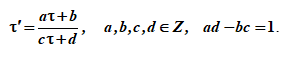
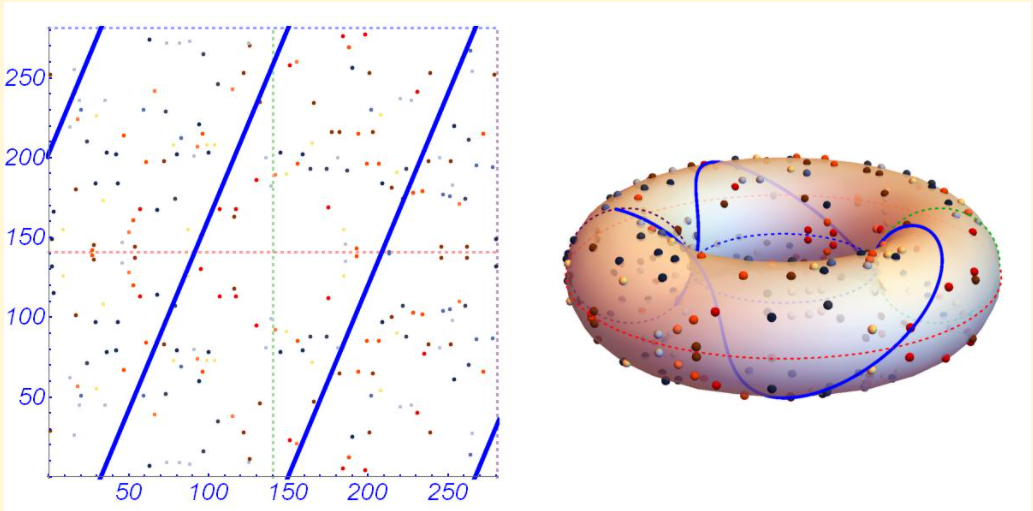





 Рассмотрим в пространстве связку с центром в ()О и плоскость p не проходящую через ()О и зададим отображение j плоскости p в связку с центром в ()О по закону: «()А плоскости p ставится в соответствии прямая ОА.
Рассмотрим в пространстве связку с центром в ()О и плоскость p не проходящую через ()О и зададим отображение j плоскости p в связку с центром в ()О по закону: «()А плоскости p ставится в соответствии прямая ОА.