Уравнение плоскости в пространстве линейная алгебра

Уравнение плоскости, виды уравнения плоскости

В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.

Определение уравнения плоскости

Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.

Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.

Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.

Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.

Общее уравнение плоскости

Сформулируем теорему, а затем запишем уравнение плоскости.

Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве

Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.

Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.

Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.

Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .

Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.

Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.

Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .

Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.

Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.

Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.

Нормальное уравнение плоскости

Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .

Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.

n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1

То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.

Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.

Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.

Уравнение плоскости в отрезках

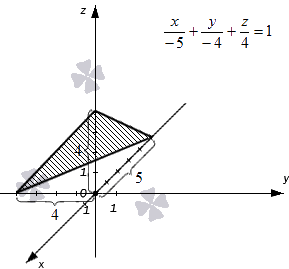
Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.

Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .

Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.

Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .

Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.

Общее уравнение плоскости

Время чтения: 34 минуты

Пространственная геометрия не сложнее обычной. Данная тема включает изучение науки о векторах и подробного понимания обычной геометрической науки.

В этой статье будем рассматривать общие уравнения плоскости. Также разберем практические примеры, проанализируем неполное общее уравнение плоскости и проходящих прямых линий.

Что называют общим уравнением плоскости

Поговорим об уравнении плоскости для трехмерного пространства.

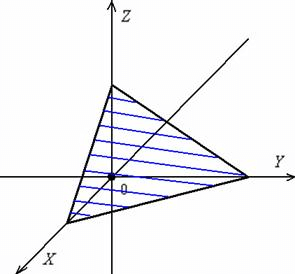
Плоскость в трехмерном пространстве

Разбираясь в чертежах, необходимо знать стандартные обозначения.

Все геометрические плоскости обычно прописывают прописными буквами греческого алфавита, а прямые обозначают большими буквами. Иногда для обозначения плоскости используют греческий алфавит, но с подстрочными индексами снизу. Чтобы изобразить плоскость, необходимо нарисовать параллелограмм, который создаст впечатление плоскости в пространстве.

Поскольку плоскость является бесконечной структурой, мы сможем отобразить лишь ее небольшой кусок. Поэтому вокруг параллелограмма изображают неровный овал, произвольной формы.

В реальности плоскости могут быть расположены в любом произвольном порядке, иметь любой наклон или угол.

Если имеется прямоугольная система координат, расположенная в трехмерном пространстве, то в уравнении будут 3 неизвестных. Чтобы добиться равенства, нужно поставить в уравнение координаты точки, которая расположена именно в данной плоскости.

Если будут поставлены координаты другой точки, не из данной плоскости, тождество не получится.

Представим, что в 3-х мерном изображении и прям-ной координатной системы Oxyz общее уравнение плоскости, проходящей через две линии, имеет 3 неизвестных: x, yes и z. Они удовлетворяют координатам плоскости.

Значит, что при использовании этих данных для каждой из точек, лежащей на плоскости, обязательно должно получиться равенство. Если равенства нет, то точка к плоскости не относится.

Для записи общего уравнения плоскости через точку, необходимо вспомнить определение прямой линии, перпендикулярной заданной плоскости.

Каждая прямая будет перпендикулярной к плоскости, если она перпендикулярна относительно прямой, принадлежащей данной плоскости. Это значит, что каждый нормальный вектор, соответствующий исходной плоскости, будет перпендикуляром к нулевому вектору, принадлежащему плоскости. Это является доказательством теоремы, которая будет определять вид общего уравнения плоскости.

Это значит, что каждый нормальный вектор, соответствующий исходной плоскости, будет перпендикуляром к нулевому вектору, принадлежащему плоскости. Это является доказательством теоремы, которая будет определять вид общего уравнения плоскости.

Уравнение для плоскости, которая проходит через 3 точки

Если 3-мерном пространстве дана прямоугольная к-ная система, она обозначена обычно Oxyz.

Тогда уравнение, где данные a, b и C являются действительными числами больше нуля, именуется ур-ем плоскости на отрезки.

При абсолютном значении чисел a, b и с, они будут равны длине отрезков, обрезанных плоскостью по осям координат. Буквенные значения демонстрируют положительное или отрицательное направление линейных сегментов относительно оси координат.

Чтобы составить общее уравнение для исходной плоскости, можно применить следующую теорему.

Любое уравнение, имеющее стандартный вид, имеет действительные значения A, b, C и D, которые не должны быть равны нулю. Эти данные определяют исходную плоскость в системе координат Oxyz, расположенной в 3-мерном пространстве.

Эта теорема содержит в себе 2 части:

Сначала получаем общее уравнение для плоскости, которая будет проходить через точку и саму плоскость.
Затем мы доказываем, что данное уравнение можно использовать для действительных чисел, чтобы доказать, что оно будет определять плоскость V, Z и D.

Доказательство 1 части:

Так как значения чисел A, V и Z не будут равны нулю одновременно, значит есть определенная точка, координаты которой будут соответствовать исходному уравнению, то есть выдавать верное равенство.
Далее вычитаем правую и левую части полученного уравнения из данного уравнения. Получается уравнение, которое будет эквивалентно исходному.
Далее необходимо будет доказать, что полученное уравнение будет определять именно плоскость в данной системе координат 3-мерного пространства и найти общее уравнение для этой плоскости.

Главным условием для перпендикулярности 2 векторов является их равенство. То есть, когда координаты удовлетворяют уравнению, то векторы будут перпендикулярны и наоборот. При верном равенстве набор точек будет обуславливать плоскость, проходящую через эту точку.

Полученное уравнение будет определять плоскость, расположенную в 3-мерном пространстве. Также оно будет полностью соответствовать для общего уравнения плоскости, которая проходит через три точки.

Из сказанного следует, что любое уравнение, эквивалентное исходному, будет определять одну и ту же плоскость. Мы доказали 1 часть теоремы.

Доказательство 2 части теоремы:

Когда имеем плоскость, проходящую через точку, вектор которой нормален, мы можем доказать, что в прям-ной координатной системе Oxyz ее задают с помощью данного основного уравнения.

Если взять любую точку данной системы координат, то векторы будут перпендикулярны, а произведение будет равно нулю.

После принятия данного понятия, уравнение снова изменится и будет определять нашу плоскость.

Вывод: если уравнения эквивалентны, то они определяют одинаковую плоскость. Мы доказали теорему.

Данный обзор будет полезен при решении математических задач, а также в аналитической геометрии.

Общее уравнение плоскости в линейных сечениях и ее вид

Принятое общее уравнение плоскости обычно имеет следующий вид: A x+B y+C z+D= Ax+By+Cz+D = 0.

Оно в основном используется только для 3-мерного пространства и прям-ной координатной системы.

Если задано общее уравнение плоскости, и имеется действительное число, неравное нулю. Оно может задать определенную плоскость, совпадающую с исходной, определяемой уравнением выше и определит точки трехмерного пространства.

Допускаем, что исходная прямоугольная координатная система задается в 3-мерном пространстве Oxyz.

Значит уравнение с действительными ненулевыми данными a, b и C — это уравнение плоскости на отрезки. Эти абсолютные значения a, b и C будут равны длине отрезков, которые ограничены исходной плоскостью.

Обозначения a, б и C будут демонстрировать направление линейных сегментов относительно осей координат. Поэтому координаты точек будут удовлетворять формуле общего уравнения плоскости.

В этой координатной системе плоскость и уравнение полностью связаны между собой, при том условии, что плоскость соответствует основному уравнению, приведенному выше.

Рассмотрим пример, соответствующий данному утверждению.

Если задана плоскость в 3-мерном пространстве и она отвечает уравнению 4x+5y–5z+20= 4x+5y–5 z+ 0 = 0, то это является описанием множества точек, изображающих данную плоскость.
Если точка находится на исходной плоскости, то можно поставить координаты этой точки в уравнение и получить абсолютное равенство.

Прямые в пространстве

Рассмотрим признаки параллельности прямых относительно заданной плоскости в пространстве:

Если 2 прямые линии в исходном пространстве параллельны, то они будут лежать в одной плоскости, поэтому пересекаться не могут.
Когда 2 линии пересекаются в пространстве, значит они не принадлежат к одной плоскости.
Когда прямая линия лежит на заданной плоскости, а другая пересекает данную плоскость в определенной точке, значит они будут пересекаться.
Прямые параллельны, если они не имеют общих точек соприкосновения.
Когда прямая не лежит на исходной плоскости, но параллельна относительно прямой, лежащей на этой плоскости, то они полностью параллельны.

Отличительные черты плоскости

Существует несколько отличительных качеств плоскости и ее параллельных линий:

Когда плоскость имеет линию (прямую) и она параллельна относительно другой плоскости, и пересекает ее, то полученная линия пересечения будет параллельна к исходной прямой.
Если две пересекающиеся плоскости, проходят через параллельные прямые, то полученная линия пересечения будет также параллельна прямым.
Когда две плоскости параллельны, то у них нет точек для соприкосновения.
Когда две прямые пересечены в одной плоскости, но параллельны относительно 2 прямых линий из другой плоскости, значит эти плоскости также параллельны.
Если прямая перпендикулярна относительно заданной плоскости, то она будет перпендикулярна относительно любой линии на плоскости.
Когда прямая перпендикулярна относительно 2-х пересекающихся прямых линий, которые лежат на плоскости, то она будет перпендикулярна к первой плоскости.

Рассмотрим еще несколько свойств перпендикулярных к плоскости линий:

Если прямая перпендикулярна относительно 1 из двух параллельно расположенных плоскостей, то она перпендикулярна и второй плоскости.
Когда 1 из двух параллельных перпендикулярна данной плоскости, другая прямая также расположена перпендикулярна к исходной плоскости.
Любая из прямых, пересекающих плоскость, когда она не является перпендикуляром, будет наклонной относительно заданной плоскости.
Когда любая плоскость перпендикулярна относительно прямой, значит она будет перпендикулярна и другой прямой.

Теорема о трех перпендикулярах на плоскости

Чтобы прямая линия, которая лежит в данной плоскости, была к ней перпендикулярна, вполне достаточно, чтобы она была перпендикулярна к проекции данной плоскости.

Любой угол между линией и плоскостью — это угол между линией и ее выступом на плоскости. Когда прямая b наклонна к исходной плоскости, то прямая а будет проекцией этой наклонной, а угол α будет находиться между наклонной и заданной плоскостью.

Любая прямая, которая получена при пересечении 2 плоскостей, будет называться ребром двугранного угла. Полуплоскости с одним общим ребром называют треугольными угловыми гранями.

Если граница полуплоскости совпадает с краем двугранного угла и делит двугранный угол на два равных, то ее называют биссектрисой.

Угол с двойными стенками можно измерять соответствующим линейным углом. Линейный угол для любого двугранного угла является углом между перпендикулярами, проведенными к каждой грани, и ее краем.

Изображение плоскости

В повседневной жизни многие предметы имеют прямоугольную форму, их поверхность имеет геометрическую плоскость.

Это книжный переплет, оконное стекло, поверхность стола и пр. Более того, глядя на эти предметы под углом и с большого расстояния, мы думаем, что они имеют форму параллелограмма. Поэтому плоскость на рисунке принято изображать в виде параллелограмма

Обычно эта плоскость обозначается одной буквой, например: «плоскость М».

Плоскость и ее основные свойства

Рассмотрим свойства плоскости, которые обычно принимаются без доказательств, поскольку это аксиомы:

Когда каждые 2 точки, которые лежат на одной прямой, принадлежат к единой плоскости, то все точки, находящиеся на этой прямой, также будут принадлежать к данной плоскости.
Если 2 плоскости соприкасаются в одной точке, значит они будут пересекаться на прямой линии, проходящей через эту точку.
Для любых 3 точек, не принадлежащих одной прямой, можно нарисовать плоскость, причем только одну.

Последствия этих аксиом следующие:

Можно нарисовать плоскость, имеющую прямую линию и точку за ней. Действительно утверждение, что точка вне прямой линии вместе с любыми двумя точками, лежащими на прямой, буду образовывать три точки, через которые может пройти новая плоскость.
Через две пересекающиеся линии можно провести единственную плоскость. Если взять точку пересечения и еще одну точку на прямой, то получим 3 точки, через которые можно будет провести единственную плоскость.
Только одну плоскость можно нарисовать двумя параллельными линиями. Доказано, что две параллельные прямые по определению лежат в одной плоскости. Эта плоскость уникальна, потому что не более одной плоскости можно провести через одну параллельную плоскость и одну точку в другую.
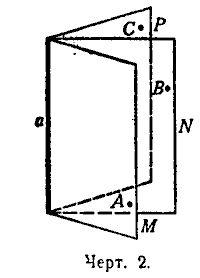
Вращение плоскости по прямой. Поэтому можно провести бесчисленное количество плоскостей через любую линию в пространстве.

Действительно, пусть это будет прямая линия.
Возьмите отдельно точку А.
Через А и данную прямую а проходит плоскость М.
Возьмем точку B, лежащую вне данной плоскости М.
Через данную точку В и прямую линию также будет проходить плоскость N, которая может не совпадать с М. Это связано с тем, что она имеет точку B и она не принадлежит к М плоскости.
Мы можем взять другую точку С в пространстве за плоскости М и N.
Через точку С и прямой пройдет новая плоскость, например Р. Она не совпадет с М, ни с N, потому что содержит точку С, которая не принадлежит плоскости М и плоскости N.

Продолжая занимать все новые и новые точки в пространстве, мы получаем все больше и больше плоскостей. Они все будут пересекать исходную линию.

Их может быть бесчисленное число. Все полученные плоскости можно рассматривать как различные повороты одной исходной плоскости, которая может будет вращаться вокруг прямой А.

Таким образом, мы можем найти еще одно качество плоскости, которая может вращаться вокруг прямой, принадлежащей к ней.

Строительные задания в пространстве

Все планиметрические конструкции выполнены с помощью чертежных инструментов с использованием единой плоскости. Обычные инструменты рисования больше не подходят, так как вы не можете рисовать символы в пространстве.

Кроме того, при объемном строительстве в пространстве, появляется необходимость в построении еще одного нового элемента — новой плоскости. Ее невозможно построить в пространстве такими простыми средствами.

Поэтому при строительстве в пространстве, строителям необходимо точно знать, как лучше построить ту или иную конструкцию.

Во всех конструкциях в пространстве мы можем предполагать следующие качества:

Плоскость можно выстроить, если найдены элементы, точно определяющие ее положение в исходном пространстве. Мы можем построить плоскость, если она будет проходить через 3 заданные точки, через прямую линию и наружную точку. А также иметь 2 пересекающиеся или две параллельные прямые.
При условии, что даны 2 пересекающиеся плоскости, то обязательно будет существовать и линия их пересечения, которую можно легко найти.
Если дана плоскость в пространстве, то можно легко сделать любые планиметрические конструкции.

Создание любой конструкции в пространстве означает сокращение ее до конечного числа указанных базовых структур. Эти базовые знания можно использовать для решения более сложных задач.

Именно так решаются задачи построения стереометрии.

Пример задания на построение в пространстве

Задача.

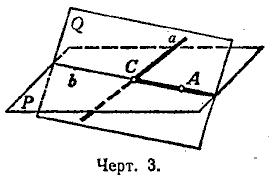
Нужно обнаружить точку, где будут пересекаться заданная прямая А с плоскостью Р. Затем необходимо составить нужное уравнение для прямой, проходящей через заданные точки: А (1; 2) и B (-1; 1).

Решение:

подставляем в уравнение (8) х 1 = 1, y 1 = 2, х 2 = -1; y 2 = 1;
получаем либо 2y-4 = х-1, либо х-2y + 3 = 0.

Каноническое уравнение прямой

Пусть декартова система координат будет установлена на плоскости Оху.

Задача: получить простое уравнение и если она является точкой прямой и и вектор кода прямой И.

Возьмем любую точку А на плоскости Р.
Через данную точку А и исходную прямую а проведем простую плоскость Q. Она будет пересекать плоскость Р вдоль новой прямой b.
В плоскости Q находим точку С — пересечение прямых линии а и b.
Эта точка будет желательной. Если прямые а и b окажутся параллельными, то у проблемы не будет решения.

Рассмотрим уравнение прямой, которая является линией пересечения двух плоскостей:

Бесчисленные плоскости проходят через каждую прямую в пространстве.
Любые два из них, пересекающиеся, определяют его в пространстве.
Это значит, что уравнения для 2 плоскостей, вместе взятые, представят собой уравнение для прямой.

Вывод:

Любые 2 непар-ные плоскости, когда они заданы единым уравнением, можно определить по линии их взаимного пересечения. Эти уравнения именуют общими простыми уравнениями.

Рассмотрим уравнение прямой линии, проходящей через две точки:

Заданы точки А (1х; 1у) и B (2х; 2у).
Уравнение для прямой, проходящей через точки А (1х; 1у) и B (2х; 2у), когда они лежат на прямой, параллельной оси О х (y 2 -y 1 = 0) или оси О y (2х -1х = 0), то уравнение будет иметь вид: y = 1у или х = 1х.

Пусть будет плавающая точка, принадлежащая прямой А. Тогда получаем направляющий вектор для прямой А, он будет иметь идентичные координаты. Набор всех точек на данной плоскости определит прямую, проходящую через точку и имеющую вектор направления, при условии, что векторы коллинеарны.

Каноническое уравнение для прямой, лежащей на плоскости, можно задать в прям-ной системе к-т Оху, как прямую, проходящую через точку и имеющую свой вектор направления.

Пример канонического уравнения

Если уравнение является каноническим для прямой, то она должна соответствовать этому уравнению и будет проходит через точку, которая является ее вектором направления.

Нужно обратить внимание на следующие важные факты:

Если направляющий вектор — это прямая линия, которая проходит через точку, то ее каноническое ур-ние можно составить.
Когда один вектор является направляющим для прямой, то каждый из векторов также будет направляющим для заданной прямой.
Поэтому каждое уравнение для любой другой прямой в канонической форме будет соответствовать заданной прямой.

Уравнения прямых и плоскостей

Поверхности и линии первого порядка.

Уравнение первой степени, или линейное уравнение, связывающее координаты точки в пространстве, имеет вид
$$
Ax+By+Cz+D = 0,\label
$$
причем предполагается, что коэффициенты при переменных не равны нулю одновременно, то есть $A^<2>+B^<2>+C^ <2>\neq 0$. Аналогично, линейное уравнение, связывающее координаты точки на плоскости, — это уравнение
$$
Ax+By+C = 0,\label
$$
при условии $A^<2>+B^ <2>\neq 0$.

В школьном курсе доказывается, что в декартовой прямоугольной системе координат уравнения \eqref и \eqref определяют соответственно плоскость и прямую линию на плоскости. Из теорем о порядке алгебраических линий и поверхностей следует, что то же самое верно и в общей декартовой системе координат. Точнее, имеют место следующие теоремы.

В общей декартовой системе координат в пространстве каждая плоскость может быть задана линейным уравнением
$$
Ax+By+Cz+D = 0.\nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат определяет плоскость.

В общей декартовой системе координат на плоскости каждая прямая может быть задана линейным уравнением
$$
Ax+By+C = 0,\nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат на плоскости определяет прямую.

Эти теоремы полностью решают вопрос об уравнениях плоскости и прямой линии на плоскости. Однако ввиду важности этих уравнений мы рассмотрим их в других формах. При этом будут получены независимые доказательства теорем этого пункта.

Параметрические уравнения прямой и плоскости.

Мы будем предполагать, что задана декартова система координат в пространстве (или на плоскости, если мы изучаем прямую в планиметрии). Это, в частности, означает, что каждой точке сопоставлен ее радиус-вектор относительно начала координат.

Рис. 6.1

Вектор $\overrightarrowM> = \boldsymbol-\boldsymbol_<0>$, начало которого лежит на прямой, параллелен прямой тогда и только тогда, когда $M$ также лежит на прямой. В этом и только этом случае для точки $M$ найдется такое число $t$, что
$$
\boldsymbol-\boldsymbol_ <0>= t\boldsymbol.\label
$$

Наоборот, какое бы число мы ни подставили в формулу \eqref в качестве $t$, вектор $\boldsymbol$ в этой формуле определит некоторую точку на прямой.

Уравнение \eqref называется векторным параметрическим уравнением прямой, а переменная величина $t$, принимающая любые вещественные значения, называется параметром.

Векторное параметрическое уравнение выглядит одинаково и в планиметрии, и в стереометрии, но при разложении по базису оно сводится к двум или трем скалярным уравнениям, смотря по тому, сколько векторов составляют базис.

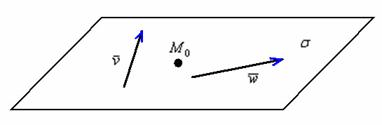
Получим теперь параметрические уравнения плоскости. Обозначим через \(\boldsymbol

\) и $\boldsymbol$ ее направляющие векторы, а через $\boldsymbol_<0>$ — радиус-вектор ее начальной точки $M_<0>$. Пусть точка $M$ с радиус-вектором $\boldsymbol$ — произвольная точка пространства (рис. 6.2).

Рис. 6.2

Вектор $\overrightarrowM> = \boldsymbol-\boldsymbol_<0>$, начало которого лежит на плоскости, параллелен ей тогда и только тогда, когда его конец $M$ также лежит на плоскости. Так как \(\boldsymbol

\) и $\boldsymbol$ не коллинеарны, в этом и только этом случае $\boldsymbol-\boldsymbol_<0>$ может быть по ним разложен. Поэтому, если точка $M$ лежит в плоскости (и только в этом случае), найдутся такие числа $t_<1>$ и $t_<2>$, что
$$
\boldsymbol-\boldsymbol_ <0>= t_<1>\boldsymbol

+t_<2>\boldsymbol.\label
$$

Это уравнение называется параметрическим уравнением плоскости. Каждой точке плоскости оно сопоставляет значения двух параметров $t_<1>$ и $t_<2>$. Наоборот, какие бы числа мы ни подставили как значения $t_<1>$ и $t_<2>$, уравнение \eqref определит некоторую точку плоскости.

Пусть $(x, y, z)$ и $(x_<0>, y_<0>, z_<0>)$ — координаты точек $M$ и $M_<0>$ соответственно, а векторы \(\boldsymbol

\) и $\boldsymbol$ имеют компоненты $(p_<1>, p_<2>, p_<3>)$ и $(q_<1>, q_<2>, q_<3>)$. Тогда, раскладывая по базису обе части уравнения \eqref, мы получим параметрические уравнения плоскости
$$
x-x_ <0>= t_<1>p_<1>+t_<2>q_<1>,\ y-y_ <0>= t_<1>p_<2>+t_<2>q_<2>,\ z-z_ <0>= t_<1>p_<3>+t_<2>q_<3>.\label
$$

Отметим, что начальная точка и направляющий вектор прямой образуют на ней ее внутреннюю декартову систему координат. Значение параметра $t$, соответствующее какой-то точке, является координатой этой точки во внутренней системе координат. Точно так же на плоскости начальная точка и направляющие векторы составляют внутреннюю систему координат, а значения параметров, соответствующие точке, — это ее координаты в этой системе.

Прямая линия на плоскости.

Поэтому мы можем сформулировать следующее утверждение.

В любой декартовой системе координат на плоскости уравнение прямой с начальной точкой $M_<0>(x_<0>, y_<0>)$ и направляющим вектором $\boldsymbol(a_<1>, a_<2>)$ может быть записано в виде \eqref.

Уравнение \eqref линейное. Действительно, после преобразования оно принимает вид $a_<2>x-a_<1>y+(a_<1>y_<0>-a_<2>x_<0>) = 0$, то есть $Ax+By+C = 0$, где $A = a_<2>$, $B = -a_<1>$ и $C = a_<1>y_<0>-a_<2>x_<0>$.

Вектор с координатами $(-B, A)$ можно принять за направляющий вектор прямой с уравнением \eqref в общей декартовой системе координат, а точку \eqref за начальную точку.

Если система координат декартова прямоугольная, то вектор $\boldsymbol(A, B)$ перпендикулярен прямой с уравнением \eqref.

Действительно, в этом случае $(\boldsymbol, \boldsymbol) = -BA+AB = 0$.

Пусть в уравнении прямой $Ax+By+C = 0$ коэффициент $B$ отличен от нуля. Это означает, что отлична от нуля первая компонента направляющего вектора, и прямая не параллельна оси ординат. В этом случае уравнение прямой можно представить в виде
$$
y = kx+b,\label
$$
где $k = -A/B$, а $b = -C/B$. Мы видим, что к равно отношению компонент направляющего вектора: $k = a_<2>/a_<1>$ (рис. 6.3).

Рис. 6.3. k=-1. Прямая y=-x+1/2

Отношение компонент направляющего вектора $a_<2>/a_<1>$ называется угловым коэффициентом прямой.

Угловой коэффициент прямой в декартовой прямоугольной системе координат равен тангенсу угла, который прямая образует с осью абсцисс. Угол этот отсчитывается от оси абсцисс в направлении кратчайшего поворота от $\boldsymbol_<1>$ к $\boldsymbol_<2>$ (рис. 6.4).

Рис. 6.4. $k=\operatorname\varphi = -1$. Прямая $y=-x+1/2$

Положив $x = 0$ в уравнении \eqref, получаем $y = b$. Это означает, что свободный член уравнения $b$ является ординатой точки пересечения прямой с осью ординат.

Если же в уравнении прямой $B = 0$ и ее уравнение нельзя представить в виде \eqref, то обязательно $A \neq 0$. В этом случае прямая параллельна оси ординат и ее уравнению можно придать вид $x = x_<0>$, где $x_ <0>= -C/A$ — абсцисса точки пересечения прямой с осью абсцисс.

Векторные уравнения плоскости и прямой.

Параметрическое уравнение плоскости утверждает, что точка $M$ лежит на плоскости тогда и только тогда, когда разность ее радиус-вектора и радиус-вектора начальной точки $M_<0>$ компланарна направляющим векторам \(\boldsymbol

\) и $\boldsymbol$. Эту компланарность можно выразить и равенством
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol

, \boldsymbol) = 0.\label
$$
Вектор \(\boldsymbol = [\boldsymbol

, \boldsymbol]\) — ненулевой вектор, перпендикулярный плоскости. Используя его, мы можем записать уравнение \eqref в виде
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol) = 0.\label
$$

Уравнения \eqref и \eqref называют векторными уравнениями плоскости. Им можно придать форму, в которую не входит радиус-вектор начальной точки. Например, положив в \eqref $D = -(\boldsymbol_<0>, \boldsymbol)$, получим
$$
(\boldsymbol, \boldsymbol)+D = 0.\label
$$

Для прямой на плоскости можно также написать векторные уравнения, аналогичные \eqref и \eqref,
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol) = 0\ \mbox<или>\ (\boldsymbol, \boldsymbol)+C = 0.\nonumber
$$
Первое из них выражает тот факт, что вектор $\boldsymbol-\boldsymbol_<0>$ перпендикулярен ненулевому вектору $\boldsymbol$, перпендикулярному направляющему вектору $\boldsymbol$, и потому коллинеарен $\boldsymbol$.

Пусть $x, y, z$ — компоненты вектора $\boldsymbol$ в общей декартовой системе координат. Тогда скалярное произведение $(\boldsymbol-\boldsymbol_<0>, \boldsymbol)$ при $\boldsymbol \neq 0$ записывается линейным многочленом $Ax+By+Cz+D$, где $(A^<2>+B^<2>+C^ <2>\neq 0)$.

Обратно, для любого линейного многочлена найдутся такие векторы $\boldsymbol_<0>$ и $\boldsymbol \neq 0$, что в заданной общей декартовой системе координат $Ax+By+Cz+D = (\boldsymbol-\boldsymbol_<0>, \boldsymbol)$.

Первая часть предложения очевидна: подставим разложение вектора $\boldsymbol$ по базису в данное скалярное произведение:
$$
(x\boldsymbol_<1>+y\boldsymbol_<2>+z\boldsymbol_<3>-\boldsymbol_<0>, \boldsymbol),\nonumber
$$
раскроем скобки и получим многочлен $Ax+By+Cz+D$, в котором $D = -(\boldsymbol_<0>, \boldsymbol)$ и
$$
A = (\boldsymbol_<1>, \boldsymbol),\ B = (\boldsymbol_<2>, \boldsymbol),\ C = (\boldsymbol_<3>, \boldsymbol)\label
$$
$A$, $B$ и $C$ одновременно не равны нулю, так как ненулевой вектор $\boldsymbol$ не может быть ортогонален всем векторам базиса.

Для доказательства обратного утверждения найдем сначала вектор $\boldsymbol$ из равенств \eqref, считая $A$, $B$ и $C$ заданными. Из ранее доказанного утверждения 10 следует, что
$$
\boldsymbol = \frac_<2>, \boldsymbol_<3>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>+\frac_<3>, \boldsymbol_<1>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>+\frac_<1>, \boldsymbol_<2>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>.\label
$$

Вектор $\boldsymbol_<0>$ должен удовлетворять условию $D = -(\boldsymbol_<0>, \boldsymbol)$. Один из таких векторов можно найти в виде $\boldsymbol_ <0>= \lambda \boldsymbol$. Подставляя, видим, что $-\lambda(\boldsymbol, \boldsymbol) = D$, откуда $\boldsymbol_ <0>= -D\boldsymbol/|\boldsymbol|^<2>$.

Итак, мы нашли векторы $\boldsymbol$ и $\boldsymbol_<0>$ такие, что линейный многочлен записывается в виде
$$
x(\boldsymbol_<1>, \boldsymbol)+y(\boldsymbol_<2>, \boldsymbol)+z(\boldsymbol_<3>, \boldsymbol)-(\boldsymbol_<0>, \boldsymbol),\nonumber
$$
который совпадает с требуемым $(\boldsymbol-\boldsymbol_<0>, \boldsymbol)$.

Если система координат декартова прямоугольная, то вектор с компонентами $A$, $B$, $C$ является нормальным вектором для плоскости с уравнением $Ax+By+Cz+D = 0$.

Это сразу вытекает из формул \eqref и доказанного ранее утверждения о нахождении компонент в ортогональном базисе.

Любые два неколлинеарных вектора, удовлетворяющие уравнению \eqref, можно принять за направляющие векторы плоскости.

Утверждение 5 нетрудно доказать и непосредственно, рассматривая координаты вектора, параллельного плоскости, как разности соответствующих координат двух точек, лежащих в плоскости.

Все, сказанное о плоскостях, почти без изменений может быть сказано и о прямых на плоскости. В частности, верно следующее утверждение.

Действительно, $\alpha_<1>, \alpha_<2>$, должны быть пропорциональны компонентам — $B$, $A$ направляющего вектора прямой.

Параллельность плоскостей и прямых на плоскости.

Ниже, говоря о параллельных прямых или плоскостях, мы будем считать, что параллельные плоскости (или прямые) не обязательно различны, то есть что плоскость (прямая) параллельна самой себе.

Прямые линии, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+C = 0,\ A_<1>x+B_<1>y+C_ <1>= 0,\nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число $\lambda$, что
$$
A_ <1>= \lambda A,\ B_ <1>= \lambda B.\label
$$

Прямые совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнения \eqref выполнено (с тем же $\lambda$) равенство
$$
C_ <1>= \lambda C.\label
$$

Первая часть предложения прямо следует из того, что векторы с компонентами $(-B, A)$ и $(-B_<1>, A_<1>)$ — направляющие векторы прямых.

Докажем вторую часть. В равенствах \eqref и \eqref $\lambda \neq 0$, так как коэффициенты в уравнении прямой одновременно нулю не равны. Поэтому, если эти равенства выполнены, уравнения эквивалентны и определяют одну и ту же прямую.

Обратно, пусть прямые параллельны. В силу первой части предложения их уравнения должны иметь вид $Ax+By+C = 0$ и $\lambda(Ax+By)+C_ <1>= 0$ при некотором $\lambda$. Если, кроме того, существует общая точка $M_<0>(x_<0>, y_<0>)$ обеих прямых, то $Ax_<0>+By_<0>+C = 0$ и $\lambda(Ax_<0>+By_<0>)+C_ <1>= 0$. Вычитая одно равенство из другого, получаем $C_ <1>= \lambda C$, как и требовалось.

Плоскости, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+Cz+D = 0,\ A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0\nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число $\lambda$, что
$$
A_ <1>= \lambda A,\ B_ <1>= \lambda B,\ C_ <1>= \lambda C.\label
$$

Плоскости совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнений \eqref выполнено (с тем же $\lambda$) равенство
$$
D_ <1>= \lambda D.\label
$$

Если плоскости параллельны, то их нормальные векторы $\boldsymbol$ и $\boldsymbol_<1>$ коллинеарны, и существует такое число $\lambda$, что $\boldsymbol_ <1>= \lambda\boldsymbol$. В силу уравнений \eqref $A_ <1>= (\boldsymbol_<1>, \boldsymbol_<1>) = \lambda(\boldsymbol_<1>, \boldsymbol) = \lambda A$. Аналогично доказываются и остальные равенства \eqref. Обратно, если равенства \eqref выполнены, то из формулы \eqref следует, что $\boldsymbol_ <1>= \lambda\boldsymbol$. Это доказывает первую часть предложения. Вторая его часть доказывается так же, как вторая часть предложения 7.

Условия \eqref выражают не что иное, как коллинеарность векторов с компонентами $(A, B)$ и $(A_<1>, B_<1>)$. Точно так же условия \eqref означают коллинеарность векторов с компонентами $(A, B, C)$ и $(A_<1>, B_<1>, C_<1>)$. Поэтому согласно ранее доказанным этому и этому утверждениям условие параллельности прямых на плоскости можно записать в виде
$$
\begin
A& B\\
A_<1>& B_<1>
\end
= 0,\label
$$
а условие параллельности плоскостей — в виде
$$
\begin
B& C\\
B_<1>& C_<1>
\end =
\begin
C& A\\
C_<1>& A_<1>
\end =
\begin
A& B\\
A_<1>& B_<1>
\end
= 0.\label
$$

Утверждению 7 можно придать чисто алгебраическую формулировку, если учесть, что координаты точки пересечения прямых — это решение системы, составленной из их уравнений.

При условии \eqref система линейных уравнений
$$
Ax+By+C = 0,\ A_<1>x+B_<1>y+C_ <1>= 0,\nonumber
$$
не имеет решений или имеет бесконечно много решений (в зависимости от $C$ и $C_<1>$. В последнем случае система равносильна одному из составляющих ее уравнений. Если же
$$
\begin
A& B\\
A_<1>& B_<1>
\end
\neq 0.\nonumber
$$
то при любых $C$ и $C_<1>$ система имеет единственное решение $(x, y)$.

Уравнения прямой в пространстве.

Прямая линия в пространстве может быть задана как пересечение двух плоскостей и, следовательно, в общей декартовой системе координат определяется системой уравнений вида
$$
\left\<\begin
Ax+By+Cz+D = 0,\\
A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0.
\end\right.\label
$$
Пересечение плоскостей — прямая линия тогда и только тогда, когда они не параллельны, что согласно \eqref означает, что хоть один из детерминантов отличен от нуля:
$$
\begin
B& C\\
B_<1>& C_<1>
\end^ <2>+
\begin
C& A\\
C_<1>& A_<1>
\end^ <2>+
\begin
A& B\\
A_<1>& B_<1>
\end^<2>
\neq 0.\label
$$

Разумеется, систему \eqref можно заменить на любую, ей эквивалентную. При этом прямая будет представлена как пересечение двух других проходящих через нее плоскостей.

Вспомним параметрические уравнения прямой \eqref. Допустим, что в них ни одна из компонент направляющего вектора не равна нулю. Тогда
$$
t = \frac><\alpha_<1>>,\ t = \frac><\alpha_<2>>,\ t = \frac><\alpha_<3>>,\nonumber
$$
и мы получаем два равенства
$$
\frac><\alpha_<2>> = \frac><\alpha_<3>>,\ \frac><\alpha_<1>> = \frac><\alpha_<3>>,\label
$$
или, в более симметричном виде,
$$
\frac><\alpha_<1>> = \frac><\alpha_<2>> = \frac><\alpha_<3>>,\label
$$
Уравнения \eqref представляют прямую как линию пересечения двух плоскостей, первая из которых параллельна оси абсцисс (в ее уравнение не входит переменная $x$), а вторая параллельна оси ординат.

Если обращается в нуль одна из компонент направляющего вектора, например, $\alpha_<1>$, то уравнения прямой принимают вид
$$
x = x_<0>,\ \frac><\alpha_<2>> = \frac><\alpha_<3>>,\label
$$
Эта прямая лежит в плоскости $x = x_<0>$ и, следовательно, параллельна плоскости $x = 0$. Аналогично пишутся уравнения прямой, если в нуль обращается не $\alpha_<1>$, а другая компонента.

Когда равны нулю две компоненты направляющего вектора, например, $\alpha_<1>$ и $\alpha_<2>$, то прямая имеет уравнения
$$
x = x_<0>,\ y = y_<0>.\label
$$
Такая прямая параллельна одной из осей координат, в нашем случае — оси аппликат.

Важно уметь находить начальную точку и направляющий вектор прямой, заданной системой линейных уравнений \eqref. По условию \eqref один из детерминантов отличен от нуля. Допустим для определенности, что $AB_<1>-A_<1>B \neq 0$. В силу утверждения 9 при любом фиксированном $z$ система уравнений будет иметь единственное решение $(x, y)$, в котором $x$ и $y$, разумеется, зависят от $z$. Они — линейные многочлены от $z$: $x = \alpha_<1>z+\beta_<1>$, $y = \alpha_<2>z+\beta_<2>$.

Не будем доказывать этого, хотя это и не трудно сделать. Для ясности, заменяя $z$ на $t$, получаем параметрические уравнения прямой
$$
x = \alpha_<1>t+\beta_<1>,\ y = \alpha_<2>t+\beta_<2>,\ z = t.\nonumber
$$

Первые две координаты начальной точки прямой $M_<0>(\beta_<1>, \beta_<2>, 0)$ можно получить, решая систему \eqref при значении $z = 0$.

Из параметрических уравнений видно, что в этом случае направляющий вектор имеет координаты $(\alpha_<1>, \alpha_<2>, 1)$. Найдем его компоненты в общем виде. Если система координат декартова прямоугольная, векторы с компонентами $(A, B, C)$ и $A_<1>, B_<1>, C_<1>$ перпендикулярны соответствующим плоскостям, а потому их векторное произведение параллельно прямой \eqref, по которой плоскости пересекаются. Вычисляя векторное произведение в ортонормированном базисе, мы получаем компоненты направляющего вектора
$$
\begin
B& C\\
B_<1>& C_<1>
\end,\
\begin
C& A\\
C_<1>& A_<1>
\end,\
\begin
A& B\\
A_<1>& B_<1>
\end.\label
$$

Вектор с компонентами \eqref есть направляющий вектор прямой с уравнениями \eqref, какова бы ни была декартова система координат.

Согласно утверждению 5 каждый ненулевой вектор, компоненты которого $(\alpha_<1>, \alpha_<2>, \alpha_<3>)$ удовлетворяют уравнению $A\alpha_<1>+B\alpha_<2>+C\alpha_ <3>= 0$, параллелен плоскости с уравнением $Ax+By+Cz+D = 0$. Если, кроме того, он удовлетворяет уравнению $A_<1>\alpha_<1>+B_<1>\alpha_<2>+C_<1>\alpha_ <3>= 0$, то он параллелен и второй плоскости, то есть может быть принят за направляющий вектор прямой. Вектор с компонентами \eqref ненулевой в силу неравенства \eqref. Непосредственно легко проверить, что его компоненты удовлетворяют обоим написанным выше условиям. На этом доказательство заканчивается.

источники:

http://www.napishem.ru/spravochnik/matematika/obschee-uravnenie-ploskosti.html

http://univerlib.com/analytic_geometry/vector_algebra/lines_and_planes_equations/