Уравнение плоскости в пространстве r3

Уравнение плоскости, виды уравнения плоскости

В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.

Определение уравнения плоскости

Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.

Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.

Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.

Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.

Общее уравнение плоскости

Сформулируем теорему, а затем запишем уравнение плоскости.

Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве

Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.

Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.

Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.

Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .

Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.

Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.

Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .

Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.

Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.

Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.

Нормальное уравнение плоскости

Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .

Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.

n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1

То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.

Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.

Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.

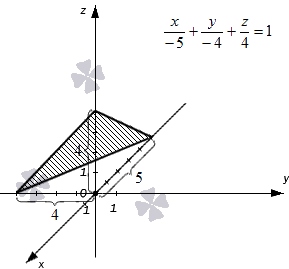
Уравнение плоскости в отрезках

Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.

Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .

Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.

Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .

Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.

Глава VIII

1. Прямые и плоскости в пространстве R n

Изучим пространство R n с другой точки зрения. Будем рассматривать его элементы не как векторы, а как точки, то есть А(х₁, х₂, . х_n), где х_i — координаты точки А ( i = 1, 2, . n). О(0. 0) — назовем началом координат.

Элементы R, R 2 , R 3 можно интерпретировать как координаты точек соответственно на прямой, на плоскости, в пространстве; поэтому R принято называть числовой прямой, R 2 — числовой плоскостью, R 3 — числовым пространством.

Как мы уже знаем, при n>3 непосредственное обращение к геометрии невозможно, но многие факты, относящиеся к R n , носят общий характер, не зависящий от n. Так свойства решений линейных уравнений и методы их исследования не зависят от числа переменных. Тогда можно сказать, что в этом смысле пространство R n обладает геометрическими свойствами, подобными свойствам пространств R, R 2 , R 3 . Множества точек в R 4 (“фигуры”) будем задавать с помощью уравнений, неравенств с n переменными и их систем как области их решений.

Определение 1. Область решений совместной системы линейных уравнений с n переменными ранга r назовем k-мерной плоскостью в R n , где k = n — r (k — число свободных, а r — базисных переменных.)

Отметим два случая:

1. r = n, k = 0. Система имеет единственное решение, которое представляет собой точку в R n , то есть точку можно считать нуль-мерной плоскостью.

2. r = 0, k = n. Все уравнения являются тождествами (0 = 0), все переменные свободные, область решений системы совпадает со всем пространством R n , то есть само пространство можно считать n-мерной плоскостью.

Если этих два крайних случая исключить из рассмотрения, то очевидно, что k может меняться в пределах 1 £ k £ n — 1.

Определение 2. Плоскость наибольшей возможной в R n размерности, но не совпадающей со всем пространством, то есть (n-1)-мерную плоскость, называют гиперплоскостью, а плоскость наименьшей возможной размерности, но не являющуюся точкой, то есть одномерную плоскость, называют прямой.

R — само одномерно и в нем не может быть плоскостей меньшей размерности.

R 2 — (числовая плоскость) — в нем гиперплоскость совпадает с прямой — это одномерная плоскость.

R 3 — (числовое пространство) — здесь гиперплоскостью является двухмерная плоскость, а прямой — одномерная плоскость; других плоскостей нет.

З а м е ч а н и е. При n > 3 кроме гиперплоскостей и прямой существуют плоскости промежуточных размерностей (n-2)-мерные, . трехмерные, двухмерные.

Гиперплоскость обычно задают одним линейным уравнением

в котором не все коэффициенты равны нулю, то есть

. (1.2)

Условие (1.2) равносильно тому, что ранг системы, состоящей из одного уравнения (1.1), равен 1.

Пусть теперь система состоит из двух уравнений

. (1.3)

Если ее матрица А имеет ранг 1, то

В этом случае гиперплоскости, определенные уравнениями системы (1.3), называются параллельными и, если

,

(то есть ранг расширенной матрицы равен 2), то система несовместна:

гиперплоскости, определенные уравнениями системы (1.3), не имеют общих точек (не пересекаются); если же

,

(то есть ранг расширенной матрицы равен 1), то система сводится к одному уравнению, две гиперплоскости совпадают.

И наконец, если ранг матрицы А равен 2, то система определяет (n-2)-мерную плоскость.

Прямую можно задать совместной системой линейных уравнений с n переменными ранга r = n-1. Если известны две точки А(а₁,а₂. а_n), B(b₁,b₂. b_n) прямой, то эту систему можно записать в виде

, (1.4)

где X(x₁, x₂, . x_n) — текущая переменная точка прямой.

Систему уравнений (1.4) называют уравнениями прямой, проходящей через две точки А и В.

1.1. Расстояние от точки до прямой

Рассмотрим прямую l в R 2 , заданную уравнением

А × х + В × у + С = 0

и точку М(х₁,у₁) вне данной прямой.

Обозначим через d расстояние MN (MN перпендикуляр к l). Уравнение перпендикуляра можно записать в виде В × (х — х₁) — А × (у — у₁) = 0.

или

= t, (1.5)

то есть t — коэффициент пропорциональности. Поэтому из (1.5) следует, что

. ×

C другой стороны, точка N(x₂,y₂) принадлежит l, следовательно, из (1.5) получаем

Подставим эти значения в уравнение прямой А × х + В × у + С = 0. Получим

А × х₂ + В × у₂ + С = А × (х₁ + А × t) + В × ( y₁ + В × t) + С = (А × х₁ + В × у₁ + C) + t × (А 2 + В 2 ) = 0

.

.

З а м е ч а н и е. (следствие).

(1.6)

является расстоянием от прямой до начала координат.

2. Разделив обе части общего уравнения прямой на , получим уравнение

, (1.7)

свободный член которого численно равен расстоянию прямой от начала координат. Такое уравнение прямой будем называть нормированным.

1.2. Нормированное уравнение прямой

Пусть дана прямая l. Проведем через начало координат прямую n, перпендикулярную l. Пусть Р — точка пересечения прямых. Возьмем единичный вектор .

Выразим уравнение l через два параметра:

и угол q

Пусть М(х,у) принадлежит l. Тогда проекция на ось, определяемую вектором , равна р, то есть при условии пр_n , так как единичный вектор, то согласно определению скалярного произведения пр_n ,= . Так как , а вектор , то скалярное произведение имеет вид

.

Следовательно, точка М принадлежит прямой l означает, что координаты этой точки удовлетворяют уравнению

. (1.8)

Это и есть нормированное уравнение прямой l.

Пусть теперь имеем общее уравнение прямой l:

l: А × х + В × у + С = 0

l:

t × A = Cos q , t × B = Sin q , t × C = -p.

t 2 × A 2 + t 2 × В 2 = Cos 2 q + Sin 2 q = 1

t 2 × (A 2 + В 2 ) = 1 (1.9)

-нормирующий множитель.

Следовательно, чтобы получить из общего уравнения прямой

А × х + В × у + С = 0

нормированное уравнение (1.8) следует умножить его на нормирующий множитель (1.9), знак которого противоположен С.

2. Общее уравнение плоскости в R 3

Зафиксируем произвольную декартову прямоугольную систему координат O_xyz и рассмотрим произвольное уравнение первой степени

А × х + В × у + С × z + D = 0, (2.1)

где A, B, C, D — произвольные константы, хотя бы одна из которых не равна 0.

Уравнение (2.1) заведомо имеет хотя бы одно решение (x₀, y₀, z₀).

Действительно, пусть С ¹ 0, следовательно, взяв произвольные (x₀, y₀), мы получим ,

которое эквивалентно (2.1).

Рассмотрим разность между (2.1) и (2.2).

которое эквивалентно (2.1).

Докажем, что уравнение (2.2) и, стало быть, уравнение (2.1), определяет плоскость (П) в O_xyz.

,

то есть хотя бы одна координата его не равна 0.

Возьмем произвольную точку М₀(x, y, z), принадлежащую плоскости П, то есть ее координаты удовлетворяют уравнению (2.3), ибо в этом случае вектор перпендикулярен вектору ( ) и их скалярное произведение

Если точка М(x,y,z) не принадлежит плоскости П, то ее координаты не удовлетворяют (2.3), ибо в этом случае вектор не перпендикулярен вектору и (2.3) не равно нулю.

Таким образом, мы доказали следующее утверждение.

Теорема 2.1. Если в R 3 фиксирована произвольная декартова система координат O_xyz (прямоугольная), то всякое уравнение первой степени с тремя переменными x,y,z определяет относительно этой системы плоскость.

З а м е ч а н и я.

1. Уравнение (2.1) с произвольными коэффициентами А, В, С (хотя бы один из которых не должен быть равен нулю) называется общим уравнением плоскости в R 3 .

2. Если два общих уравнения

А × х + В × у + С × z + D = 0

определяют одну и ту же плоскость, следовательно, существует число t, такое, что справедливы равенства

Рассмотреть(самостоятельно) неполные уравнения плоскости, когда

1) А = 0; 2) В = 0; 3) C = 0; 4) D = 0;

5) A = В = 0; 6) A = C = 0; 7) B = C = 0;

8) A = В = C = 0; 9) A = C = D = 0; 10) В = C = D = 0;

2.1. Угол между двумя плоскостями

Пусть даны две плоскости П₁ и П₂, которые заданы уравнениями

Чтобы определить угол между плоскостями, достаточно определить угол j между их нормальными векторами и .

По определению скалярного произведения

. (2.5)

Условие параллельности двух плоскостей заключается в пропорциональности координат векторов и :

. (2.6)

Условие “плоскость П₁ перпендикулярна к плоскости П₂” определяет, что Cos j = 0

2.2. Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой

Пусть даны три точки М₁(x₁,y₁,z₁), М₂(x₂,y₂,z₂) и М₃(x₃,y₃,z₃). Необходимо вывести уравнение плоскости, проходящей через эти три точки. Так как эти три точки не лежат на одной прямой, то векторы и неколлинеарны, и поэтому точка М(x,y,z) лежит в одной плоскости с точками М₁, М₂ и М₃ в том случае, если векторы , и компланарны.

Теорема 2.2. Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы выполнялось следующее условие

(2.8)

Из условия (2.8) получим уравнение первой степени относительно x,y,z. Оно и является уравнением искомой плоскости.

2.3. Нормированное уравнение плоскости. Отклонение точки от плоскости

Пусть дана плоскость П. Проведем через начало координат прямую n перпендикуляр к плоскости П, и пусть Р — точка пересечения прямой n и плоскости П.

Рассмотрим вектор и — единичный вектор. . Пусть углы a , b , g образованы с положительными направлениями осей и вектором . Тогда . Очевидно, что точка М(x,y,z) принадлежит плоскости П тогда, когда проекция вектора на ось, определяемую вектором , равна р.

пр_n = р = .

Так как , то скалярное произведение равно р

(2.9)

Определение 2.1. Назовем отклонением d точки М от плоскости П число +d в случае, когда точка М и начало координат точка О лежат по разные стороны от плоскости П, и число -d — в случае, когда точка М и начало координат точка О лежат по одну сторону от плоскости П, (куда направлен вектор — “+d” и “-d” — в противоположном расположении точки М, если точка О лежит на плоскости).

Для нахождения отклонения d точки М₀(x₀,y₀,z₀) от плоскости П следует в левую часть нормированного уравнения плоскости П поставить на место х,у,z координаты x₀,y₀,z₀ точки М.

А × х + В × у + С × z + D = 0

определяют одну ту же плоскость, то существует t такое, что

t × A = Cos a , t × B = Sin b , t × C = Sin g , t × D = -p.

Так как сумма квадратов направляющих косинусов равна 1, то

t 2 × (A 2 + B 2 + C 2 )=1,

, (2.10)

где знак t противоположен знаку коэффициента D.

Для приведения общего уравнения плоскости

А × х + В × у + С × z + D = 0

к нормированному виду (2.9) следует умножить его на нормирующий множитель (2.10), знак которого противоположен знаку коэффициента D.

3. Прямая линия R 3

Прямую в пространстве R 3 можно задать как пересечение двух плоскостей, определяемых уравнениями

(3.1)

Приведем (3.1) к каноническому виду.

Для этого достаточно найти:

1) хотя бы одну точку М₁(x₁,y₁,z₁), через которую проходит прямая

Так как плоскости, определяемые (3.1), не параллельны и не сливаются, то нарушается (2.6), то есть хотя бы одна из пропорций

,

а это значит, что хотя бы один из определителей второго порядка

, ,

отличен от нуля.

.

Тогда, взяв вместо z произвольное число z₁ и подставив его в уравнение (3.1), можно определить соответственно x₁ и y₁

(3.2)

Можно взять z₁=0. Тогда, воспользовавшись (3.2), получим, что прямая проходит через точку .

Пусть текущая точка М(x,y,z). Тогда уравнение линии можно записать в виде

. (3.3)

. (3.4)

Уравнение прямой, проходящей через данную точку М₁(x₁,y₁,z₁) и перпендикулярной плоскости А × х + В × у + С × z + D = 0, имеет вид

. (3.5)

Уравнение прямой, параллельной данной плоскости и проходящей через данную точку М₀(x₀,y₀,z₀).

Пусть плоскость П задана уравнением

Тогда уравнение прямой имеет вид

4. Выпуклые множества точек на плоскости. Неравенства

4.1. Неравенства

Пусть задана линия

то есть это множество точек, координаты которых удовлетворяют этому уравнению. Аналогично можно рассмотреть множество точек, координаты которых удовлетворяют неравенству

(х — a) 2 + (у — b) 2 — r 2 = 0

Это уравнение определяет окружность с центром в точке С(a,b) радиуса r, (Рис. 8.4);

(х — a) 2 + (х — b) 2 — r 2 0

определяет множество точек, лежащих внутри круга с центром в точке С(a,b) радиуса r, (Рис. 8.5);

(х — a) 2 + (х — b) 2 — r 2 > 0

определяет множество точек, лежащих вне этого круга с центром в точке С(a,b) радиуса r (Рис. 8.6);

Множество точек, удовлетворяющих (4.1), называют областью решений этого уравнения.

Аналогично будем говорить об области решений неравенств (4.2) и (4.3).

Пусть теперь F(x, y) — линейное уравнение, то есть имеет вид

F(x, y) = A × x + B × y + C, (4.4)

где A, B, C — константы .

Любое невырожденное уравнение A × x + B × y + C = 0 определяет линию L в R 2 , рассмотрим

A × x + B × y + C 0 (4.5)

A × x + B × y + C > 0, (4.6)

По отношению к прямой линии все точки разбились на два множества Ф₁ и Ф₂, лежащие по разные стороны от прямой L (Рис 8.7).

Покажем, что эти множества определяются неравенствами (4.5) и (4.6).

Так как эти точки не лежат на прямой, то имеем

Действительно, так как точки М₁(х₁,у₁), М₂(х₂,у₂) лежат по разные стороны от прямой (4.4), то существует точка М₀(х₀,у₀) такая, что она делит отрезок М₁М₂ в отношении , а сама точка М₀(х₀,у₀) принадлежит прямой L, то есть

, . (4.7)

Так как точка М₀(х₀,у₀) принадлежит прямой L, то имеем

Подставим (4.7) в (4.4):

.

то есть d ₁+ l × d ₂ = 0, откуда d ₁ = -l × d ₂ , но l > 0, следовательно, d ₁ и d ₂ имеют разные знаки.

Пусть, например, d ₁ 0, d ₂ > 0, тогда точка М₁(х₁,у₁) удовлетворяет неравенству (4.5), а точка М₂(х₂,у₂) — неравенству (4.6).

Множество точек, лежащих на некоторой прямой и по одну сторону от нее, называют полуплоскостью.

Очевидно, что каждая прямая L разбивает плоскость П на две полуплоскости, для которых она является общей границей. Считается, что граница принадлежит сразу двум полуплоскостям.

Если (4.4) — это граница, то нестрогие неравенства

A × x + B × y + C £ 0

A × x + B × y + C ³ 0

Пусть задана система неравенств

(4.8)

Геометрически система (4.8) может быть истолкована как область решений этой системы, то есть это множество точек , которые одновременно удовлетворяют всем неравенствам этой системы, то есть . Очевидно, что область решений системы неравенств является пересечением областей решений каждого из неравенств системы.

З а м е ч а н и е. В частности может иметь место .

Областью решений системы линейных неравенств

(4.9)

является очевидно пересечение полуплоскостей, определяемых каждым из неравенств.

Эту область будем называть многоугольником.

Не исключены также случаи вырождения многоугольной области в прямую или луч, а многоугольника — в отрезок или точку.

4.2. Выпуклые множества точек на плоскости

Определение 4.1. Множество точек называется выпуклым, если вместе с двумя его точками М₁ и М₂ ему принадлежат и все внутренние точки отрезка М₁М₂.

Выпуклые множества: полуплоскость, круг, отрезок и так далее.

Многоугольники могут быть как выпуклые, так и невыпуклые. Геометрически это можно всегда увидеть, но этот факт также может быть

установлен и аналитически.

Теорема 4.1. Пусть дана полуплоскость

Ф₁: A × x + B × y + C 0

Если А × х₀ + В × у₀ + С 0, то тогда полуплоскость будет выпуклой.

Д о к а з а т е л ь с т в о :

Координаты точки М₁ можно выразить через координаты точек М₁ и М₂:

, ,

Подставим эти выражения в неравенство полуплоскости

.

l > 0, и по условию

а по определению 8.4 такое множество называется выпуклым.

З а м е ч а н и е. Определение выпуклого множества сформулировано в предположении, что в этом множестве имеются по крайней мере две точки. Если множество пустое (в этом случае его обозначают как Æ ) или состоит из одной точки, то его тоже считают выпуклым.

Для выпуклых множеств имеет место следующая теорема:

Теорема 4.2. Пересечение любого числа выпуклых множеств — выпуклое множество.

Д о к а з а т е л ь с т в о :

Пусть j ₁, j ₂, . j _n — выпуклые множества и их пересечение , тогда оно выпукло. Из того, что точка М₀(х₀,у₀) принадлежит множеству j _i (i = 1. n) следует, что М₀(х₀,у₀) принадлежит .

Пусть имеем две произвольные точки М₁(х₁,у₁) и М₂(х₂,у₂), принадлежащие пересечению множеств j _i, тогда, так как все множества j _i выпуклы, то им принадлежит и отрезок М₁М₂, а следовательно, , но тогда и пересечение есть множество выпуклое.

Следствие. Область решений системы линейных неравенств (), если она не представляет собой Æ , является выпуклой многоугольной областью или выпуклым многоугольником.

5. Выпуклые множества в пространстве. Неравенства

По аналогии с пространством R 2 можно рассмотреть геометрию и неравенства в пространстве R 3 .

определяют множество точек пространства, координаты которых удовлетворяют этим неравенствам.

(х — a) 2 + (х — b) 2 + (z — c) 2 2

определяет внутреннюю область шара, ограниченную сферой

(х — a) 2 + (х — b) 2 + (z — c) 2 = r 2

с центром в точке С(а,b,c) и радиусом r, а неравенство

(х — a) 2 + (х — b) 2 + (z — c) 2 > r 2

определяет множество точек, находящихся вне этого шара.

Множество точек, лежащих в некоторой плоскости и по одну сторону от нее, называют полупространством.

5.1. Нестрогие линейные неравенства

D + A × x + B × y + C × z и

D + A × x + B × y + C × z > 0

определяют два полупространства, общей границей которых будет плоскость

D + A × x + B × y + C × z = 0.

Доказательство этого факта проводится так же, как и в случае двух переменных.

Пусть дана система линейных неравенств с тремя неизвестными

. (5.3)

Областью решений системы (5.3) является пересечение полупространств, то есть такое множество точек, если оно не пусто, которое является решением каждого из неравенств системы. Это пересечение полупространств называют многогранной областью или (в случае ограниченности) многогранником.

З а м е ч а н и е.

1. Понятие выпуклого множества точек и теорема о выпуклости пересечения выпуклых множеств точек сохраняет силу и для пространства.

(Провести доказательство самостоятельно).

2. Так как полупространство выпукло, то область решений системы линейных неравенств (5.3), если она не пуста, является выпуклой многогранной областью (или выпуклым многогранником), если она ограничена.

Не исключены случаи вырождения.

Назад Далее

75. Различные уравнения плоскости

Пусть в пространстве R 3 Задана прямоугольная система координат Oxyz.

Определение 1. Нормальным вектором плоскости A называется любой ненулевой вектор N Перпендикулярный плоскости A.

Пусть N = (A,B,C) ≠ 0, — нормальный вектор плоскости a, M0(X0,Y0,Z0)- точка, принадлежащая плоскости a. Пусть M(X,Y,Z), произвольная точка пространства,

.

Тогда точка M принадлежит плоскости a тогда и только тогда, когда векторы и N Ортогональны. Два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю, Последнее в ортонормированном базисе можно записать в виде:

Таким образом, получаем уравнение плоскости, Проходящей через точку и перпендикулярной вектору N = (A,B,C) ≠ 0.

Рассмотрим произвольное уравнение первого порядка

Где коэффициенты одновременно не равны нулю, т. е. A2+ B2+ C2 ≠ 0.

Теорема 1. Любую плоскость в произвольной аффинной системе координат можно задать уравнением (1) первого порядка и обратно любое уравнение (1) первого порядка в аффинной системе координат определяет плоскость.

Доказательство. Достаточно доказать теорему для прямоугольной системы координат. Любую плоскость в прямоугольной системе координат можно задать ее нормальным вектором N = (A,B,C) ≠ 0 И точкой M0(X0,Y0,Z0), принадлежащей плоскости. Уравнение этой плоскости выведено в §2.2 и имеет вид:

Где D = —Ax0 — By0 — Cz0. Так (A,B,C) ≠ 0, то A2+ B2+ C2 ≠ 0 и любая плоскость есть поверхность первого порядка.

Обратно, пусть некоторая поверхность в пространстве определена уравнением (1). Так как не все коэффициенты равны нулю, то уравнение (1) имеет решение (X0,Y0,Z0). Тогда

И точка M0(X0,Y0,Z0) принадлежит поверхности. Вычитая почленно из уравнения (1) равенство (2), получим уравнение

Равносильное уравнению (1). Это уравнение в силу §2.2, определяет плоскость, проходящую через точку M0(X0,Y0,Z0), перпендикулярную вектору N = (A,B,C).

Определение 2. Направляющими векторами плоскости A называется пара неколлинеарных векторов S1 И S2 Параллельных плоскости A.

Пусть S1 = (M1,K1,L1), S2 = (M2,K2,L2) — направляющие вектора плоскости a, M0(X0,Y0,Z0)- точка, принадлежащая плоскости a. Пусть M(X,Y,Z), произвольная точка пространства,

.

Тогда точка M принадлежит плоскости a тогда и только тогда, когда векторы , S1 и S2 компланарны. Три вектора компланарны тогда и только тогда, когда определитель, составленный из координат этих векторов равен нулю. Таким образом, получаем уравнение плоскости по Двум направляющим векторам и точке, принадлежащей плоскости

. (4)

Пример 1. Найдем уравнение плоскости с направляющими векторами S1 = (B,—A,0), S2 = (C,0,—A), где A ≠ 0. Так как векторы S1 и S2 неколлинеарны, то формуле (4) находим уравнение этой плоскости:

.

.

Сократим на A ≠ 0 и получаем уравнение

. (5)

Рассмотрим радиус вектора RO = и R =. Точка M принадлежит плоскости a тогда и только тогда, когда векторы = R — RO, S1 и S2 компланарны. Так как векторы S1 и S2 неколлинеарны, то последнее равносильно тому, что вектор R — RO линейная комбинация векторов S1 и S2, т. е. R — RO = US1 +VS2, где U, V — действительные числа.

Отсюда получаем так называемое Векторно-параметрическое уравнение Плоскости.

Где U, V — произвольные действительные параметры.

Так как R == (X,Y,Z), RO = = (X0,Y0,Z0), то запишем это уравнение в координатной форме. Получим Параметрические уравнения плоскости:

(7)

Где U, V — произвольные действительные параметры, S1 = (M1,K1,L1), S1 = (M2,K2,L2) — направляющие вектора плоскости, M0(X0,Y0,Z0)- точка, принадлежащая плоскости.

Пусть даны три точки M1(X1,Y1,Z1), M2(X2,Y2,Z2), M3(X3,Y3,Z3) плоскости, которые не принадлежат одной прямой. Тогда векторы ,

являются направляющими векторами плоскости a. Применяя формулу (4) получим Уравнение плоскости, проходящей через три данные точки:

. (8)

Пусть плоскость не проходит через начало координат и пересекает оси Ox, Oy, Oz Соответственно в точках M1(A,0,0), M2(0,B,0), M3(0,0,c). По формулу (8) находим уравнение плоскости, проходящей через эти три точки

.

Вычислим этот определитель и преобразуем полученное уравнение к более простому виду

. (9)

Уравнение (5) называется Уравнением плоскости в отрезках на осях.

.Замечание 1. Уравнение (1) называется Общим уравнением плоскости. Если плоскость a задается общим уравнением (1) в прямоугольной системе координат, то N = (A,B,C) — нормальный вектор плоскости a.

Если плоскость a задается общим уравнением (1) в произвольной аффинной системе координат и A ≠ 0, то S1 = (B,—A,0), S2 = (C,0,—A) направляющие вектора плоскости a.

Рассмотрим Частные случаи уравнения (1).

1. Пусть D = 0. Тогда уравнение (1) принимает вид: Ax + By + Cz = 0 и плоскость, определяемая этим уравнением, проходит через начало координат (см. Рис. 6).

2. Пусть С = 0, A ≠ 0. Тогда уравнение (1) принимает вид: Ax + By + D = 0. Рассмотрим направляющие вектора S1 = (B,—A,0) и S2 = (0,0,—A) этой плоскости. Так как базисный вектор Е3 = (0,0,1) оси Oz. коллинеарен вектору S2, то плоскость a, определяемая этим уравнением, параллельна оси Oz (см. Рис. 7).

3. Пусть B=0, С = 0, A ≠ 0. Тогда уравнение (1) принимает вид: Ax + D = 0. Рассмотрим направляющие вектора S1 = (0,—A,0) и S2 = (0,0,—A) этой плоскости. Так как базисные векторы е2 = (0,1,0), Е3 = (0,0,1) .коллинеарны соответственно векторам вектору S1, S2, то плоскость a, определяемая этим уравнением, параллельна координатной плоскости Ozy (см. Рис. 8).