Уравнение плоскости виды взаимное расположение двух плоскостей

Уравнение плоскости, виды уравнения плоскости

В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.

Определение уравнения плоскости

Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.

Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.

Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.

Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.

Общее уравнение плоскости

Сформулируем теорему, а затем запишем уравнение плоскости.

Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве

Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.

Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.

Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.

Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .

Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.

Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.

Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .

Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.

Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.

Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.

Нормальное уравнение плоскости

Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .

Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.

n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1

То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.

Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.

Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.

Уравнение плоскости в отрезках

Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.

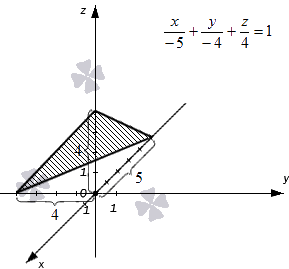
Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .

Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.

Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .

Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.

Взаимное расположение плоскостей

Параллельные плоскости

Получим условия параллельности или совпадения двух плоскостей и заданных общими уравнениями:

Необходимым и достаточным условием параллельности или совпадения плоскостей (4.23) является условие коллинеарности их нормалей Следовательно, если плоскости (4.23) параллельны или совпадают, то т.е. существует такое число что

Плоскости совпадают, если помимо этих условий справедливо Тогда первое уравнение в (4.23) имеет вид т.е. равносильно второму, поскольку

Таким образом, плоскости (4.23) параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число что но Плоскости (4.23) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны: и

Условия параллельности и совпадения плоскостей (4.23) можно записать в виде

Отсюда следует критерий параллельности или совпадения двух плоскостей (4.23):

Поверхности уровня линейного четырехчлена

Поверхностью уровня функции трех переменных называется геометрическое место точек координатного пространства в которых функция принимает постоянное значение, т.е.

Для линейного четырехчлена уравнение поверхности уровня имеет вид

При любом фиксированном значении постоянной уравнение (4.24) описывает плоскость. Рассмотрим поведение семейства поверхностей уровня, отличающихся значением постоянной. Поскольку коэффициенты и не изменяются, то у всех плоскостей (4.24) будет одна и та же нормаль Следовательно, поверхности уровня линейного четырехчлена D представляют собой семейство параллельных плоскостей (рис.4.19). Поскольку нормаль совпадает с градиентом (см. пункт 3 замечаний 4.2), а градиент направлен в сторону наискорейшего возрастания функции, то при увеличении постоянной поверхности уровня (4.24) переносятся параллельно в направлении нормали.

Пересекающиеся плоскости

Необходимым и достаточным условием пересечения двух плоскостей (4.22) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:

При этом условии система уравнений

имеет бесконечно много решений, которые определяют прямую пересечения плоскостей, заданных уравнениями (4.23).

Угол между плоскостями

Угол между двумя плоскостями можно определить как угол между их нормальными векторами. По этому определению получаются не один угол, а два смежных угла, дополняющих друг друга до В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина угла между двумя плоскостями удовлетворяет условию

Если — нормали к плоскостям и соответственно (рис.4.20,а), то величина угла между этими плоскостями вычисляется по формуле:

Необходимым и достаточным условием перпендикулярности плоскостей (4.23) является условие ортогональности их нормалей, т.е.

При пересечении двух плоскостей образуются четыре двугранных угла (рис.4.20). Величина двугранного угла удовлетворяет условию

получаем острый двугранный угол , образованный плоскостями (4.23), если 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAOQAAAAUCAMAAACqG2GmAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMA2+pwDT6+X6AdLK9Qy49/usJWAwAAA2ZJREFUWMPlV9mCpCAMlDPc8P9fuxwRBNF153GHF7ujhlSlkuBx/K7FzYNd/0cgrd/bpf/qgam6LFtoAbTH73QZ5RMJXMvZrKOk1JrDmo9u+PxfJLJ9zqXPIAXQxADAp7DYSbXLpD6KyiYlDg6S2Mkek3XZnbf0kxtHlZcTsT6l7X7kAXy+JVaLboRwmpZblOAesA1m4dsQ0t63Kc7Q2+ss2U+clyjUNXoWaOKbJ2Pcgy+Q1D3rEcG4ZbuAQbOdI6UXXimqkU1k9bfNzY1j/KH+xIVXTnLKNiWjSU6L/goytKB0onyRGWCGzQeQsmMQV1le8nd3AzKsUfJaHPxSIgGyb7HZ3x0kmafmsFp8FYP2ZPEkK0/cUrdveXqWQ6fIXNR6rYGdWp1fYJoGb1SbkUUN9xCEPPbg6011446GvPwqphxftUe+d+Sn6Oy+PbHH3jCCVWaqkQayq0GWEkWVXOYi96bYm9ac+RtIl6wQAjzuJcZ2stilqhYh+CtIupCtNWKfW7bbUC+sHVZAkGdLcVJrHWrXAEXhMviyvdU7sEi7eDSUFWW9uEtJQi9JE7wcScCSpPrggUlixnApi7B60SiHUR78Eo8f3SabRWDEboRhrDSd8imTnMi8SKVKawKj6zR7AZdzCn33B5Bn6yrNlee5PQSosTQhd/Gcq15TbguSX4pe8wRLx+ay9gqza9U6ELfIFVUeGIqthdpBKmitMZQsFK/wKleckmcTHSBxSh6ldUS/zK6bXEeja/LGXVXHxPIPWbgKm3OSu4TTuqvE2XtWzgxS+Ku2Cwv6FSRg1cTGVgeJlGbVypYjot5AhhMNNNIR5JmDrEiOIOAm1cni/ZiphsTpXHeCFIShd4x27ZorSFUFlWu7YekgW6nqmBCMI/wNZD4LiNYQ+BXkmUqHTB3BPjcdJD1LIlBd1ZFq0ZVrbS3kHNypeNXlSlkX9SNIWR/M66QTQSq0J3meV6R+7a4HV/lsrnpWesJioirIcw65CaObxwfSQKIi+/lHYP+JwQ4j3kfIciCU+3NSHv3wCjI/42B8PwxVcgd9/JTNhxsXtqcyA/AwmvcgQTKmxBLKD0ByHxksJxbG3/xsD/XGMxbjT78qwSai7puaVNY/fD6bLFO7YUEVP+q7n1jiuSux1MD+k+a3rj+cGyJvT1X7swAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> (рис.4.20,а), и тупой в противном случае: (рис.4.20,б). Другими словами, по формуле (4.26) находится тот двугранный угол, образованный плоскостями, в котором лежат точки, принадлежащие разноименным полупространствам, определяемым данными плоскостями. На рис.4.20 изображены пересекающиеся плоскости, положительные и отрицательные полупространства отмечены знаками + или – соответственно.

Пример 4.10. Найти величину того угла, образованного плоскостями и внутри которого лежит точка

Решение. По уравнениям плоскостей находим нормали а также величину угла между нормалями, используя (4.26):

Подставляя координаты точки в левые части уравнений плоскостей, выясняем, каким полупространствам принадлежит эта точка. Для плоскости имеем 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAN8AAAARBAMAAACvNWTbAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMAYP4P3segIFPuP7ONfi1w1Fgf5QAAAqVJREFUOMtjYKA7KAAjCDBGYkMA3wMEm/0BhmZhJFl0uXcYqu3AZOa2nQdgIk1hOwNQlDC6uS6AsblcZ15AM4FRHc60SkGTE02NQBPhcfMBUUlKjnChT0pzDFDUrHzAqgFjlxZw60DtgQlVwi3kmT0FLWjmMQShhchJg0qQ13KWI4R+r0O1j+HSBjYdGPtmA5cSRJoFJrQF4UMGF1Sd/NoMh0DG8zbARJjnMvAqA+l8JFXf0EP9dQPCh5cSGCYtQLGQMQ23hXw7GIJAMcB+FBbPjIoMjCDD8qsQ6eSbFUa6MHKGsewLGCYVoFhYaobbQqCPVMCqma9+hvB5tRg4dIF0aqw3PBxbYrag2VjojZRs+VQZUCzcxYbHQnaRcKjFXy9DohlooRqQTmOw3AASBoktNWCbjqqtZyvYBRAnsc5DsZDxAMRCA6wWMp6Gp1KR4yCSDWohmAXMEQkQZaA0wigIApDY5p4FsgnijJ8LIJKSgoISQJapAdhCqCkQC8E6JSD2JMHTS+thJAsfMLDpAykhkDcfgxIXqoWMKiAL9UBMDj8QaQi2UBDIyl21WgPoBA5tHBY2OcAsXL0dGqS6YPeBLeQDBaumAb82SrhcM+BSAkYiMzgilz7gf4AcpKmhkaoJYCdjCVLedIZFsBju3gXOKIqghAqylFsPlq5UGfh1UBKakgCjJjzJhDOwPkDNh6y4Ew2TIkOTArTMyYOkIl0GXqB6dj+GlxtgqnYwmDqjaAs1YNOFFytTXJwMiLaQNZjh0AVIIj0OKyYYTEA2LcmZBs8WpTmuqNmidE8SvKBNUlJCyxY8kzRhRS+jp9IUAZRcEX1MB5INL8OETONDQTaxdyDsYG5cjJa4F/ZhqWBYiKmFuCTA5vJ+Rgg1LiCzRuOnoDYEAJ1BjPvu16j0AAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> значит, точка лежит в положительном полупространстве, определяемом плоскостью Для плоскости имеем 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAMYAAAARBAMAAAB0js75AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAYQ6sm+EgQMJ68VMw0spZRHUAAAJySURBVDjLvZXNa9RAGMafzWa/SJBOD3oQlhSsiMqyUAUtKBVq/QDFr9iDCKs9KIJSxc+DotVCW3sI0kK9iEqVirisgngQS0EQW6EsiBcV6bpL17aav8HMTCbZGbrrzRySd57MvL/MM+9MgP9yfQjDHGDJLzcqbVk4qebSmlSFdXn99WAg7Nw05Eg91hwv5yQh9WJiKmhMd6sZU3OKcGnbMJDo034UhLLfPeZH/vfcxWSRRxf4YwQzT0XvM/1VP9ogpBmFkVjCZgt6N9IHhLTjsoi4ZJYRK3Ghiz8mrFQlyBAVjB5hVT9jXAv81IuYbUJ0AZmfQtoFmZFYtPSKxMhPGX/qM1JjjBEZFAavzyKTRbwZmYcB41ROYuAN9AWJ8QlGuT7j4zrulXHHz3OuAytYqnRWDNq99bAlMYDW3xLDm36pPmM46a9Hoo1Xxg2foX2heTUq7aGTkxlpR2HMsh7WcoyUIxgw23rZaI9BJf07bbUzDUk67CUhjwhhpWU+o/fzhAwSspIt62d6jx0KGS2EjBGyyotOI2DA3EJnMukx6EqMMu+20wLu5U5wRjOVzzoKI8qm0fo4ZJxgjNVedOvK9arYPfF9hdArow/3vNZaWg8V6EuSV9o3TMtedUKnem45rwYGhn511CJoUWVuAletwPxICcl5iREt4L7E0B28r7/miM0Jp/gmTnr7w0HiiW0XxfyO0mKrZbTb9nOJ8cC2x//NMPiKe19dxd4ckq7rBrX7rnNcqt2I93K+lqF5QlC7sbx7RGZE84s0l3E7ONNGR9QzLf5W2YPh1dXo6O6RmxfDc9QkVt1Rjiq8asRoafjz+Avab6T1GhuezwAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> значит, точка лежит также в положительном полупространстве, определяемом плоскостью Поскольку точка принадлежит одноименным полупространствам (положительным), то искомый угол — это угол смежный найденному углу

Пучки плоскостей

Собственным пучком плоскостей называется совокупность всех плоскостей, проходящих через фиксированную прямую ( ось пучка ).

Несобственным пучком плоскостей называется совокупность плоскостей, параллельных фиксированной плоскости (осью несобственного пучка плоскостей считается бесконечно удаленная прямая).

Любые две плоскости и определяют пучок плоскостей, содержащий заданные плоскости и Если плоскости и пересекаются, то прямая пересечения является осью собственного пучка (рис.4.21,а). Если плоскости и параллельны, то они определяют несобственный пучок параллельных плоскостей (рис.4.21,б).

Пусть заданы уравнения двух плоскостей (4.23):

Линейной комбинацией этих уравнений называется уравнение

где числа — коэффициенты линейной комбинации. Его можно записать в форме

Заметим, что линейная комбинация уравнений является уравнением первой степени для любых значений коэффициентов, кроме случая, когда все коэффициенты при неизвестных равны нулю, т.е. при одновременном выполнении условий

Эти значения параметров считаются недопустимыми.

Уравнение (4.27) называется уравнением пучка плоскостей, содержащего плоскости

При любых допустимых значениях параметров уравнение (4.27) задает плоскость, принадлежащую пучку, и наоборот, для любой плоскости пучка найдутся такие значения параметров что уравнение (4.27) будет задавать эту плоскость.

Доказательство утверждения аналогично доказательству свойства пучка прямых.

Пример 4.11. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей и через точку

Решение. Искомая плоскость входит в пучок плоскостей, задаваемый уравнением (4.27)

Подставляя координаты точки получаем:

Возьмем, например, и подставим в уравнение пучка:

Итак, искомое уравнение получено.

Связки плоскостей

Собственной связкой плоскостей называется совокупность всех плоскостей, проходящих через фиксированную точку ( центр связки ).

Несобственной связкой плоскостей называется совокупность плоскостей, параллельных фиксированной прямой (центром несобственной связки плоскостей считается бесконечно удаленная точка).

Уравнение собственной связки плоскостей с центром имеет вид

где — произвольные параметры, одновременно не равные нулю.

Уравнение связки плоскостей (собственной (рис.4.22,а) или несобственной (рис.4.22,6)) можно получить в виде линейной комбинации уравнений трех плоскостей:

где — коэффициенты линейной комбинации. Заметим, что линейная комбинация уравнений является уравнением первой степени для любых значений коэффициентов, кроме случая, когда все коэффициенты при неизвестных равны нулю. Эти значения параметров считаются недопустимыми.

Уравнение (4.28) называется уравнением связки плоскостей, содержащей три плоскости

При любых допустимых значениях параметров уравнение (4.28) задает плоскость, принадлежащую связке, и наоборот, для любой плоскости связки найдутся такие значения параметров что уравнение (4.28) будет задавать эту плоскость.

Доказательство утверждения аналогично доказательству свойства пучка прямых.

Общее уравнение плоскости. Различные виды уравнения плоскости

Плоскостью называется поверхность, вес точки которой удовлетворяют общему уравнению: Ax + By + Cz + D = 0, где А, В, С – координаты вектора -вектор нормали к плоскости.

Возможны следующие частные случаи:

А = 0 – плоскость параллельна оси Ох

В = 0 – плоскость параллельна оси Оу

С = 0 – плоскость параллельна оси Оz

D = 0 – плоскость проходит через начало координат

А = В = 0 – плоскость параллельна плоскости хОу

А = С = 0 – плоскость параллельна плоскости хОz

В = С = 0 – плоскость параллельна плоскости yOz

Уравнение плоскости, проходящей через три точки.

Для того, чтобы через три какие-либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.

Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М₁, М₂, М₃ необходимо, чтобы векторы были компланарны. ( ) = 0

Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости.

Пусть заданы точки М₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂) и вектор .

Уравнение плоскости по одной точке и двум векторам, коллинеарным плоскости.

Пусть заданы два вектора и , коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы должны быть компланарны.

Уравнение плоскости по точке и вектору нормали.

Уравнение плоскости в отрезках.

Если в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на -D

, заменив , получим уравнение плоскости в отрезках: ; Числа a, b, c являются точками пересечения плоскости соответственно с осями х, у, z.

Уравнение плоскости в векторной форме.

где – радиус- вектор текущей точки М(х, у, z),

– единичный вектор, имеющий направление, перпендикуляра, опущенного на плоскость из начала координат.

,  и  – углы, образованные этим вектором с осями х, у, z.

p – длина этого перпендикуляра.

В координатах это уравнение имеет вид: xcos + ycos + zcos – p = 0.