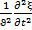Уравнение бегущей волны. Волновое уравнение
Лекция 6. Механические волновые процессы
План лекции
6.1. Возникновение волны. Продольные и поперечные волны.
6.2. Уравнение бегущей волны. Волновое уравнение.
6.3. Фазовая и групповая скорости.
6.4. Волны в упругих средах.
6.5. Звук и его характеристики.
6.6. Элементы акустики и их значение в строительстве.
6.7. Использование энергии упругих волн в строительстве.
Возникновение волны. Продольные и поперечные волны
Если в среде колеблется частица, то она приводит в колебание соседние частицы. Процесс распространения колебаний называется волной. Направление распространения колебаний называется лучом. В зависимости от направления колебаний частиц относительно луча различают волны продольные и поперечные. Если колебания происходят вдоль луча, то волна продольная, а если колебания перпендикулярны лучу — волна поперечная. Продольные волны распространяются в средах, в которых возникают упругие силы при деформациях растяжения – сжатия (разрежения – уплотнения), то есть в твердых, жидких и газообразных телах. Поперечные волны распространяются в средах, в которых возникают упругие силы при деформациях сдвига, т.е. в твердых телах. Таким образом в жидкостях и газах возникают только продольные волны, а в твердых телах – как продольные, так и поперечные.
Поверхность, до которой дошли колебания частиц к моменту времени t, называется фронтом волны. Совокупность точек (частиц), колеблющихся в одинаковых фазах, образует волновую поверхность. Если фронт волны плоский, волна называется плоской. Если фронт волны представляет собой поверхность шара, волна называется сферической. Так волна, распространяющаяся от точечного источника в однородной среде, будет сферической.
При волновом процессе точка среды совершает колебания относительно положения равновесия и почти не имеет поступательного перемещения вдоль луча. От источника поступательно перемещаются фаза и энергия колебаний. Соответственно скорость перемещения фазы – фазовая скорость, перенос энергии – групповая скорость.
Уравнение бегущей волны. Волновое уравнение
Уравнение бегущей волны выражает зависимость смещения колеблющейся частицы от координаты и времени.
Рассмотрим вывод уравнения плоской синусоидальной волны. Пусть упругая волна распространяется вдоль оси x. Если ξ(x,t)= Asinωt будет уравнением колебания точки (частицы), то такие же колебания частицы, отстоящей от источника на расстоянии x, произойдут позже, то есть с опозданием на время x/υ. Точка (частица) на расстоянии x будет иметь такое смещение в момент времени t , как и начальная точка в момент (t -x/υ). Тогда уравнение колебаний частиц, колеблющихся в плоскости XOY, или уравнение плоской бегущей волны будет:
Если фазовая скорость имеет обратное направление (-υ), то есть волна распространяется в обратном направлении, то
Без учета поглощения энергии в общем случае уравнение плоской синусоидальной волны, распространяющейся вдоль положительного направления оси OX, будет:
где A — амплитуда волны,
φ0— начальная фаза колебаний, определяемая выбором начала отсчета x и t ;
[ω(t ± x/υ) + φ0] — фаза плоской волны.
Введем в уравнения (6.1) и (6.2) волновое число:
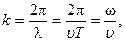
где λ — длина волны;
T — период колебаний;
ω — циклическая частота.
Обобщив (6.1), (6.2) и (6.3), перепишем уравнение плоской бегущей волны в виде:
Направление волны зависит от знака (+) или (-) перед kx.. .
Аналогично можно показать, что уравнение сферической синусоидальной волны (её волновые поверхности имеют вид концентрических сфер) записывается так:
ξ(r,t) = 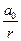
где 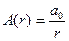
a0 — физическая величина, численно равная амплитуде на единичном расстоянии от центра волны.
Из (6.5) видно, что амплитуда колебаний сферической синусоидальной волны не остается постоянной, а убывает с расстоянием r от источника по закону 1/r .
Существуют и другие формы записи синусоидальной плоской и сферической волны 1 .
 |
1 Основываясь на формуле Эйлера, уравнения этих волн в экспоненциальной форме можно записать так:
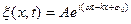
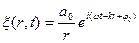
Уравнение волны (6.4) – одно из возможных решений общего дифференциального уравнения с частными производными, описывающее процесс распространения возмущения в среде. Такое уравнение называется волновым. Его можно получить продифференцировав (6.4) по два раза, сначала по t, а затем по x:
Сравнивая эти уравнения получим волновое уравнение для плоской волны, распространяющейся вдоль оси OX:
Волновое уравнение в общем случае:
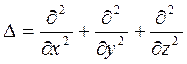
Дата добавления: 2015-10-26 ; просмотров: 4018 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
ВЫВОД УРАВНЕНИЯ БЕГУЩЕЙ ВОЛНЫ
Читайте также:
|
|
ПОЛУЧЕНИЕ КОГЕРЕНТНЫХ ПУЧКОВ С ПОМОЩЬЮ ЗЕРКАЛА ЛЛОЙДА:
|
ПОЛОСЫ РАВНОГО НАКЛОНА — чередующиеся тёмные и светлые полосы (интерференционные полосы), возникающие при падении света на плоскопараллельную пластину в результате интерференции лучей, отражённых от верхней и нижней её поверхностей и выходящих параллельно друг другу.
Просветление оптики — создание покрытий на поверхности оптических деталей, в первую очередь линз.
Голография — «трёхмерную фотографию». По интерференционной картине можно выявлять и измерять неоднородности среды. Также интерференционные волны от отдельных «элементарных» излучателей используют при создании сложных излучающих систем (антенн) для электромагнитных и акустических волн.
ИНТЕРФЕРОМЕТР МАЙКЕЛЬСОНА—двулучевой интерферометр,состоящий из светоделительного зеркала, разделяющего входящий луч на два, которые в свою очередь, отражаются зеркалом обратно. На полупрозрачном зеркале разделённые лучи вновь направляются в одну сторону, чтобы смешавшись на экране, образовать интерференционную картину.
ИНТЕРФЕРОМЕТР ЖАМЕНА — двулучевой интерферометр, использовавшийся для измерения малых показателей преломления газов. В интерферометре Жамена свет проходит через две одинаковые плоскопараллельные стеклянные пластины толщиной не менее 20 мм. Они устанавливаются под углом в 45° к линии, которая соединяет их центры и поворачиваются с помощью винтов относительно вертикальной и горизонтальной осей для изменения ширины интерференционных полос. При падении пучка света на первую пластину, он частично отражается от её внешней и внутренней поверхностей, расщепляясь на два луча. При этом расстояние между лучами зависит от толщины пластины. Интерференция возникает после отражения от второй пластины между лучами, каждый из которых испытал по одному отражению от разных поверхностей пластин.
ИНТЕРФЕРОМЕТР ФАБРИ-ПЕРО — многолучевой интерферометр, состоящий из двух стеклянных или кварцевых пластинок, обращённые друг к другу и параллельные между собой, на поверхности которых нанесены зеркальные покрытия с высоким (85—98%) коэффициентом отражения. Параллельный пучок света, падающий из объектива, в результате многократного отражения от зеркал образует большое число параллельных когерентных пучков с постоянной разностью хода D=2nhcos(φ) между соседними пучками, но различной интенсивности. В результате многолучевой интерференции в фокальной плоскости объектива образуется интерференционная картина, имеющая форму концентрических колец с резкими интенсивными максимумами, положение которых определяется из условия D=mλ (m — целое число), т. е. зависит от длины волны.
РАСЧЕТ ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЫ ОТ 2Х КОГЕРЕНТНЫХ ИСТОЧНИКОВ
|

Разность фаз δ=φ1-φ2=ω(t- L1/v1) – ω(t- L2/v2)=ω(L2n2 – L1n1)=
=(2ω/c)*(L2n2 – L1n1)=(2π/λo)*(L2n2 – L1n1);
L*n=S – оптическая длина пути. L2n2 – L1n1=S1 – S2 = ∆ — оптическая разность ходов, δ=2π∆/λo => если на оптическую разность хода ∆=+-kλo=+- 2k*(λi/2), k=0,1,2…, δ=+ — (2π/λo)*kλo=+ — 2kπ. Волны приходят в одинаковых фазах и их амплитуда складывается. Это условие интерференционного максимума. Если ∆=+ — (2k+1)*(λo/2), то δ=+ — (2π/λo)*(2k+1)*(λo/2)=+ — (2k+1)π Волны, приходят в противофазе, т.е. они антифазны и при наложении в т. Р, их амплитуда будет вычитаться. Значит это условие интерференционного минимума. Применим это условие при расчете интерференционной картины от 2х когерентных источников. Два когерентных источника S1 и S2, расстояние между ними d: Опред. рез. наложения волн в точке Р: ∆/d=x/L, т.к. L>>d, то BP≈L, тогда ∆=dx/L. Если ∆Єz, то в точке светлая полоса, x=L∆/d; ∆x=Lλ/d – ширина темной полосы. Для монохромных волн à max расх. ∆=0, ∆φ=0, кроме max центральн.
Дата добавления: 2015-01-30 ; просмотров: 38 | Нарушение авторских прав
Бегущие электромагнитные волны
Бегущие волны – это волны, которые переносят энергию в пространстве. Количественно транспортирование энергии этой волной назначает вектор плотности потока энергии, называемый вектором Умова-Пойтинга. Его направление совпадает с направлением распространения энергии. Модуль вектора равняется энергии, которую может переносить волна за время, равное 1 с , через площадку, располагаемую перпендикулярно к направлению ее движения с площадью, равняющуюся 1 .
Уравнение плоской бегущей волны
Для получения уравнения бегущей волны рассматривается плоская гармоническая. Считается, что она распространяется по О х . Поверхности волны перпендикулярны О х , все точки волновой поверхности совершают колебания одинаково, смещение ξ = ξ ( x , t ) будет функцией с координатой x и временем t . Запись уравнение колебаний частиц, находящихся на плоскости х , примет вид:
ξ ( x , t ) = A cos ω t — x υ ( 1 ) .
Отсюда ξ ( x , t ) является периодической по времени и по координате х . уравнение ( 1 ) называют уравнением бегущей волны. Если плоская волна задается при помощи выражения ( 1 ) , то ее перемещение идет по О х . При обратном ее направлении по О х уравнение запишется как:
ξ ( x , t ) = A cos ω t + x υ ( 2 ) .
Если волна движется по О х без поглощения энергии, то это характеризуется уравнением:
ξ ( x , t ) = A cos ω t — x υ + φ 0 ( 3 ) .
Значение A = c o n s t относят к амплитуде, ω – к циклической частоте волны, φ 0 — к начальной фазе колебаний, определяемой выбором началом отсчета x и t , ω t — x υ + φ 0 – к фазе плоской волны.
Что называют электромагнитной волной. Волновое число
Электромагнитные волны – это распространяющиеся в пространстве изменения состояния электромагнитного поля. Они характеризуются волновым числом k .
Запись выражения ( 1 ) примет совершенно другой вид при известном волновом числе.
Если перейти к комплексным числам, применив формулу Эйлера, уравнение плоской волны зафиксируем.
Выражение ( 6 ) имеет физический смысл только в действительной части, но R e возможно опустить в записи уравнения волны.
Перейдем к рассмотрению волнового процесса, где не происходит изменение фазы.
Далее найдем дифференциал от выражения ( 7 ) .
При условии, что υ волны зависит от частоты колебаний, то такая волна подвержена дисперсии.
Уравнение сферической бегущей волны
Сферическая волна – это волна, волновая поверхность которой является концентрической сферой. Такое уравнение примет вид:
ξ ( r , t ) = A 0 r cos ω t — k r + φ 0 ( 11 ) ,
где r является расстоянием от центра волны до точки рассмотрения. Если имеем дело со сферической волной, то ее амплитуда колебаний не будет постоянной даже при условии, что энергия не поглощается средой. Ее убывание происходит обратно пропорционально расстоянию. Выполнение уравнения ( 8 ) возможно тогда, когда источник волн считается точечным.
Уравнение бегущей волны в любом виде подчинено волновому уравнению.
Дана плоская электромагнитная волна в вакууме, которая распространяется по О х . Амплитуда напряженности электрического поля равняется E m . Определить амплитуду напряженности магнитного поля заданной волны.
За основу необходимо принять выражение для амплитуд электромагнитной волны:
ε ε 0 E = μ μ 0 H ( 1 . 1 ) .
Запись уравнения колебаний модуля E → в электромагнитной волне при условии, что она является плоской и идет по О х , фиксируем:
E = E m cos ω t — k x ( 1 . 2 ) .
Для записи уравнения колебаний H → в электромагнитной волне, в случае если она считается плоской и распространяется по О х :
H = H m cos ω t — k x ( 1 . 3 ) .
Из условия имеем, что волна производит рассеивание в вакууме, то ε = 1 , μ = 1 . Применяя ( 1 . 1 ) , ( 1 . 2 ) , ( 1 . 3 ) :
ε 0 E m = μ 0 H m → H m = ε 0 μ 0 E m .
Ответ: H m = ε 0 μ 0 E m .
Распространение электромагнитной плоской волны идет в вакууме по О х . Ее падение производится перпендикулярно поверхности тела, которое способно полностью поглощать волну. Значение амплитуды напряженности магнитного поля равняется
H m . Определить давление волны на тело.
Необходимо учитывать, что тело, которое поглощает падающую на него энергию, оказывается под давлением, равным среднему значению объемной плотности энергии в электромагнитной волне.
Следует применять соотношение амплитуд электромагнитной волны, которое записывается:
ε ε 0 E = μ μ 0 H .
Для того, чтобы зафиксировать уравнение колебаний E при распространении волны по О х , получим:
E = E m cos ω t — k x .
Теперь перейдем к уравнению колебаний H , если рассеивание плоской волны идет соответственно направлению О х . Запишем:
H = H m cos ω t — k x .
Следует, что значение объемной плотности электрической энергии примет вид:
ω E = ε ε 0 E 2 2 .
Формула плотности магнитного поля:
ω H = μ μ 0 H 2 2 .
Причем ω E = ω H . Запись примет вид:
ω = ω E + ω H = 2 ω H = μ μ 0 H 2 = μ μ 0 H m 2 cos 2 ω t — k x .
После усреднения плотности, имеем:
» open=» ω = » open=» μ μ 0 H m 2 cos 2 ω t — k x .
При » open=» cos 2 ω t — k x = 1 2 получаем:
p = » open=» ω = μ μ 0 H m 2 2 .
Ответ: p = » open=» ω = μ μ 0 H m 2 2 .
http://lektsii.net/2-15022.html
http://zaochnik.com/spravochnik/fizika/volnovaja-optika/beguschie-elektromagnitnye-volny/
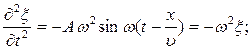
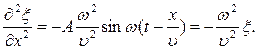
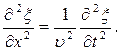
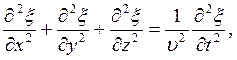
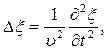

 cos
cos