4.1. Плоская электромагнитная волна в диэлектрике. Скорость распространения электромагнитной волны
При исследовании процессов в переменном электромагнитном поле пользуются полной системой уравнений Максвелла.
Здесь 

где r+ и r— – объемная плотность положительно заряженных частиц и отрицательно заряженных частиц, перемещающихся в пространстве со скоростью 
Для плоской, поляризованной электромагнитной волны, излучаемой источниками, не содержащими постоянных токов и зарядов (антенна), и распространяющейся в идеальном диэлектрике (g=0), уравнения электромагнитного поля можно преобразовать к следующему виду:
Отметим, что электромагнитная волна называется плоской, когда векторы 
Поляризованной называется такая волна, в которой вектор напряженности электрического поля все время остается параллельным некоторому направлению (например, как в нашем случае, оси ох), а вектор напряженности магнитного поля – другому (оси оy).
Такие условия обеспечиваются при излучении электромагнитных волн неподвижной антенной на достаточно большом расстоянии от нее.
Таким образом, в электромагнитной волне, свободно распространяющейся в однородном и изотропном диэлектрике, векторы 

Уравнения (4.1) и (4.2) можно преобразовать к следующему виду:


Уравнение (4.3) является уравнением колебаний или волновым уравнением и относится к гиперболическому типу.
Как известно, решение такого уравнения всегда можно представить в виде:

При этом составляющая Ех1 называется прямо бегущей или прямой волной (перемещается в положительную сторону оси oz со скоростью u), а составляющая Ех2 – обратно бегущей или обратной волной (перемещается в отрицательную сторону оси oz со скоростью u).
Используя выражения (4.1), (4.2) и (4.4) получаем формулу для напряженности магнитного поля
Составляющие Нх1 и Нх2 также называют прямой и обратной волной.
Таким образом, электромагнитная волна распространяется в пространстве со скоростью u (в прямом или в обратном направлении).
В частности, в пустоте (m=m0, e=e0) эта скорость равна скорости света (u=2.998*10 8 м/с»3*10 8 м/с).
Если существует только прямая или только обратная волна, то энергии электрического и магнитного полей равны между собой, так как при этом равны их объемные плотности

Отношение Ех1/Ну1=?`m¤e=Zв имеет размерность электрического сопротивления и называется волновым сопротивлением среды.
В частности, для пустоты Zв=377Ом (Zв =120p).
Таким образом, для любой среды

В случае, если прямая электромагнитная волна распространяется в среде, абсолютное значение магнитной проницаемости которой m=m1, а абсолютное значение диэлектрической проницаемости e=e1, и подходит нормально (перпендикулярно) к плоской границе, разделяющей данную среду и среду с m=m2 и e=e2, то прямая волна (Ех1=Еj1, Нх1=Нj1) частично будет проходить сквозь поверхность раздела, образуя во второй среде преломленную (прямую) волну (Еj2, Нj2), а частично будет отражаться от поверхности раздела, образуя в первой среде отраженную (обратную) волну (Ех2=Еy1, Нх2=Нy1).
Соотношение между напряженностями поля для этих волн на поверхности раздела можно представить следующим образом:

Если волновые сопротивления сред равны между собой (Zв1= Zв2), то отраженные волны отсутствуют.
В случае, когда источник (антенна) излучает электромагнитную волну, в которой напряженность электрического и магнитного поля изменяется по гармоническому закону, то для прямой волны
Здесь yн— начальная фаза; w – угловая частота колебаний (w=2pf).
Расстояние, на которое распространяется электромагнитная волна в течение одного периода колебаний Т (Т=1/f), называется длиной волны
Из данного выражения видно, что длина волны в диэлектрике обратно пропорциональна частоте f. Так, при частоте f=1 МГц длина волны в пустоте равна 300 м, а при f=50Гц l=6000 км.
Курс I. Уравнения Максвелла в диэлектрической среде
Уравнения Максвелла в диэлектрической среде
Уравнения Максвелла в произвольной среде таковы

система (1a) замыкается материальными соотношениями 






Заметим, что в приведенном, общепринятом виде (1a) формулировка уравнений принадлежит Герцу (Максвелл уравнения приводил в интегральной форме).
Заметим также, что система (1a) – это постулат, обобщающий все известные до Максвелла явления электричества и магнетизма (Кулон 1785 г. – закон взаимодействия электрических зарядов; Эрстед 1820 г. – магнитное действие тока, существование связи между магнитными и электрическими явлениями; Ампер – все магнитные явления в природе вызваны электрическими токами (теория молекулярных токов Ампера); Фарадей 1831 г. – электромагнитная индукция; и т. д.)
Волновое уравнение. Электромагнитная природа света.
Для интересующих нас в дальнейшем диэлектриков с 



откуда, если диэлектрическая проницаемость 

Из векторного анализа известно

тогда (1.2) принимает вид

Далее, из условия 

В результате, вместо (1.3) имеем

Аналогично, для 

В случае однородных диэлектриков 

Уравнения (1.7) называются волновыми. Их справедливость ограничена лишь требованием однородности среды и отсутствия в ней токов проводимости и свободных зарядов.
К ним относятся как граничные условия на поверхностях разделов сред, так и условия на границах рассматриваемой области пространства. Последние полностью определяются конкретными условиями задачи (например, условия на бесконечности).
Условия на границах разделов для диэлектриков (отсутствие поверхностных зарядов и токов проводимости) эквивалентны уравнениям


где индексы 1 и 2 относятся к двум граничащим средам, а t означает любое направление, касательное к поверхности раздела.
Плоские электромагнитные волны
Одним из простейших решений волнового уравнения является плоская волна.
Волна называется плоской, если в любой момент времени во всех точках произвольной плоскости, перпендикулярной направлению распространения волны, векторы поля постоянны. Если этим направлением считать ось z, то компоненты поля плоской, монохроматической волны имеют вид


где 

Подстановка (1.9) в волновые уравнения (1.7) дает


где 
Элементарно решив (1.10), найдем решения волновых уравнений в случае плоских волн в виде


каждое из которых представляет собой суперпозицию двух волн, распространяющихся в противоположных направлениях оси z. Здесь 
Обычно, в качестве решения рассматривается одна из волн, например,


С помощью найденного простейшего решения (1.12) можно продемонстрировать ряд важнейших общих свойств электромагнитных волн.
В частности, если ось z координатной системы не совпадает с направлением распространения волны, дифференцирование векторов поля по координатам сведется к их умножению на величину 



откуда следует, что векторы 


По аналогии, дифференцирование векторов поля по t сводится к их умножению на 

или, с учетом 

Последнее означает, что векторы 




Из (1.14) следует также, что 


Всегда следует помнить, что физический смысл компонент поля, записанных в комплексной форме (см., например, запись (1.12)), несут лишь действительные части этих выражений. При этом каждая из декартовых компонент электрического и магнитного векторов поля плоской, монохроматической волны имеет вид

Здесь 



Совместим ось z c 

a) Эллиптическая поляризация
После несложных математических операций исключим из (1.17) 

где 
В аналитической геометрии показывается, что (1.18) представляет собой уравнение конического сечения, а более конкретно – уравнение эллипса. Этот эллипс вписан в прямоугольник, стороны которого параллельны координатным осям 


Аналогично показывается, что конец магнитного вектора поля также описывает эллипс, вписанный в прямоугольник со сторонами в 
Из общих физических соображений следует также различать две возможные эллиптические поляризации в соответствии с направлением, в котором конец электрического вектора описывает эллипс. В литературе сформировалось определение, согласно которому правой поляризация называется, когда наблюдателю, смотрящему навстречу световому лучу, кажется, что конец электрического вектора движется по часовой стрелке. Для левой эллиптической поляризации справедливо обратное.
Поскольку параметры 
b) Линейная и круговая поляризации
Перейдем к рассмотрению частных случаев.


то эллипс (1.18) превратится в прямую линию. В самом деле, уравнение (1.18) переходит при этом в

а конец электрического вектора в прямоугольнике 
Иногда эта линейная поляризация называется еще плоской поляризацией. Понятно, что в этой ситуации магнитный вектор также линейно поляризован.
Другим частным случаем эллиптической поляризации является круговая. Переход от эллиптической к круговой поляризации происходит тогда, когда, во-первых, 


Уравнение (1.18) переходит при этом в уравнение окружности

где также различают правую и левую поляризации.
Круговая поляризация иногда называется циркулярной.
Итак, во всех случаях поляризованного света концы векторов поля в каждой точке движутся периодически. В случае же неполяризованного света они движутся совершенно нерегулярно, и такие световые колебания не имеют никаких преимущественных направлений в плоскости, перпендикулярной направлению распространения.
Основные законы оптики – преломление света, отражение, полное внутреннее
Применим теперь найденные выше для плоских волн соотношения к исследованию распространения этих волн при наличии плоской границы, разделяющей два однородных, изотропных диэлектрика, занимающих два полупространства.
В задаче о преломлении волн на границе полубесконечной среды физический смысл имеет решение, основанное на предположении о наличии трех волн: падающей, отраженной и преломленной.
Падающая на границу волна порождает новый волновой процесс.
По определению плоская волна полностью определена, если известно ее поведение во времени в некоторой точке пространства. Вторичные поля, возникающие на границе, будут так же изменяться во времени, как и первичное поле падающей волны. Поэтому переменные части фазовых множителей трех волн в произвольной точке 

где 

нения волн в обеих средах.
Выбрав в качестве границы раздела плоскость z=0, (1.21) запишем в виде

Равенства должны выполняться для любых значений x и y на границе. Это дает


откуда следует, что все три вектора 
Выберем в качестве плоскости падения плоскость xz. Тогда y-компоненты векторов 

где 

Из (1.24) и (1.23) имеем


откуда 

Из (1.25) следует также

Последнее соотношение вместе с утверждением, что нормаль 
Если 





Тогда (1.27) примет вид

Ясно также, что физический смысл имеет лишь нижний знак перед корнем во втором сомножителе в (1.28).
Из (1.28) следует, и это подтверждается опытным путем, что электромагнитное поле в среде 2 все же не равно нулю. Волна (1.28) представляет собой неоднородную волну, распространяющуюся в плоскости падения вдоль x по поверхности раздела сред и с экспоненциально падающей с ростом z амплитудой. Эта волна не является поперечной, поскольку ее компонента электрического вектора 
1. . Электромагнитные волны. Сов. Радио, 1957.
2. М. Борн, Э. Вольф. Основы оптики. М., Наука, 1970.
3. . Основы теории электричества. М., Наука, 1989.
В ИДЕАЛЬНОМ ДИЭЛЕКТРИКЕ
В природе наблюдается факт существования материального объекта – электромагнитного излучения (электромагнитных волн). Экспериментальные исследования электромагнитных волн выявили ряд свойств этого излучения. Например, электромагнитные волны оказались поперечными волнами (вспомните явление поляризации света); в электромагнитной волне, распространяющейся в диэлектрике, электрические и магнитные поля колеблются в фазе; электромагнитная волна обладает импульсом (опыты П.Н. Лебедева) и другие факты. Уравнения Максвелла как фундаментальные постулаты электродинамики согласуются с наблюдаемыми экспериментальными фактами. Отметим также, что разработка электро- и радиотехнические устройства также опирается на следствия из уравнений Максвелла. Соответствие экспериментальных результатов и выводов из уравнений Максвелла является подтверждением того, что эти уравнения адекватно описывают электромагнитные явления в макромире.
Предварительно, перед началом изучения следующих разделов, рекомендуем вспомнить волновое уравнение в струне (глава 1).
3.5.1. Из уравнений Максвелла вытекает существование
электромагнитного излучения (электромагнитной волны).
Данное утверждение можно качественно интерпретировать уравнениями Максвелла в интегральной форме. Например, если в некоторой точке пространства создать переменное электрическое поле ( 





Волновое уравнение электромагнитного излучения непосредственно вытекает из уравнений Максвелла в дифференциальной форме. Покажем это. В качестве среды вначале возьмем идеальный диэлектрик, т.е. непроводящую (плотность тока j = 0) и нейтральную среду (плотность свободных зарядов r = 0). В этом случае имеем следующую систему уравнений (см. сводную таблицу § 3.4.6):
1) ротор вектора E: [Ñ, E] = — 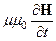
2) ротор вектора H: [Ñ, H] = 
3) дивергенция вектора E: ÑE =0,
4) дивергенция вектораH: ÑH = 0.
Возьмем ротор от первого уравнения системы уравнений (26):
[Ñ [Ñ, E]] = — 
Операция, выраженная оператором набла Ñ = 

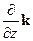


Но [Ñ, H]= 

В левой части уравнения (28) стоит двойное векторное произведение. Напомним правило двойного векторного произведения на примере векторов a, b, c:
[а,[b, c]] = b(a×c) —c(a×b).
Вначале выполняются скалярные произведения стоящих в скобах векторов (a×cи a×b), и затем векторыb и c умножаются на соответствующие результаты скалярного произведения.
Итак, имеем: [Ñ [Ñ, E]] = Ñ (ÑE) -Ñ 2 E,
где оператор Ñ 2 = ( 

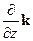


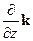


называется оператором Лапласа. Оператор Лапласа для краткости часто обозначается символом «D», т.е. Ñ 2 º D: D = 


Так как ÑE =0 [третье уравнение в системе уравнений Максвелла (26)], то: [Ñ [Ñ, E]] = -Ñ 2 E. (29)
Подставив (29) в (28), получим:
Ñ 2 E = 


Взяв теперь ротор от второго уравнения системы уравнений (26), и произведя аналогичные преобразования, получим уравнение для вектора напряженности магнитного поля:
Ñ 2 H = 


Уравнения (30) и (31) — волновые уравнения, описывающие распространение электромагнитной волны в диэлектрике. Волновые уравнения получены с использованием системы уравнений Максвелла (26). Следовательно, характеристики электромагнитной волны – векторы E иH — взаимосвязаны между собой и взаимообусловливают друг друга.
Электромагнитное поле находится в состоянии движения и распространяется в виде электромагнитной волны с фазовой скоростью c. В уравнениях (30) и (31) величина c = 

где e — электрическая проницаемость среды, m — магнитная проницаемость среды.
Представим уравнения (30) и (31) относительно декартовой системы координат в развернутом виде:










где E = Exi+ Eyj + Ezk; H = Hxi+ Hyj + Hzk.
Если волновая поверхность электромагнитной волны имеют произвольную форму, то, в общем случае, производные компонентов векторов по координатам в (32) и (33) могут принимать ненулевые значения.
Для анализа свойств электромагнитной волны рассмотрим случай, когда волновая поверхность представляет собой плоскую поверхность. Такая волна является плоской электромагнитной волной.
3.5.2. Волновое уравнение плоской электромагнитной волны в идеальном диэлектрике в отсутствии потерь. Решение волнового уравнения, свойства волны



На рис. 3-32 показаны несколько плоских волновых поверхностей электромагнитной волны. Волна распространяется в направлении оси 0Z; волновые поверхности параллельны координатной плоскости X0Y, а ось 0Z перпендикулярна волновой поверхности. Вектор v – фазовая скорость распространения электромагнитной волны.
Выпишем уравнения Максвелла относительно декартовой системы координат для непроводящей и нейтральной среды (в этих уравнениях i,j,k — орты в направлении осей x, y, z соответственно):
1) ( 






2) ( 






3) 
4) 
Два вектора равны, если равны их компоненты, поэтому, с учетом равенства нулю производных по координатам x и y, получим следующую систему уравнений:
из первого уравнения вытекают соотношения










из третьего — 
из четвертого — 
Из последнего уравнения (34) и уравнения (37) следует, что компонента напряженности магнитного поля не зависит ни от координаты z, ни от времени t, т.е. Hz = const. Аналогично, из последнего уравнения (35) и уравнения (36) следует, что компонента напряженности электрического поля Ez = const, т.к. Ez также не зависит ни от координаты z, ни от времени t. Ситуация, когда Hz = const и Ez = const означает, что на электромагнитную волну накладывается стороннее постоянное однородное магнитное и электрическое поле, а само электромагнитная волна не содержит компонентов Hz и Ez. Можно сказать по-другому: если компоненты электромагнитной волны Hz и Ez не изменяются ни во времени, ни в пространстве, то эти компоненты не существуют.
Условия, когда компоненты электромагнитной волны Hz = 0, Ez = 0означают, что векторы H и Eперпендикулярны оси 0Z и расположены в волновой поверхности, т.е. электромагнитная волна является поперечной волной. Весьма убедительным экспериментальным подтверждением поперечности электромагнитных волн являются, например, опыты по поляризации электромагнитных волн в видимом диапазоне частот — опыты по поляризации света.
Из двух первых уравнения (34) и двух первых уравнения (35) образуются две группы независимых уравнений.
Первая группа — уравнения




связывают между собой компоненты Ey и Hx.
Из первого уравнения (38) следует, что если создать переменное во времени магнитное поле Hx, направленное вдоль оси 0X, то поле Hx порождает переменное электрическое поле Ey, направленное вдоль оси 0Y. В свою очередь, из второго уравнения (38) следует, что переменное электрическое поле Ey, направленное вдоль оси 0Y, порождает переменное магнитное поле Hx, направленное вдоль оси 0X. Этот процесс периодически повторяется. Обратите внимание, в этом случае поля Ex и Hy не возникают. Векторы E и H электромагнитной волны взаимно перпендикулярны и направлены, соответственно, вдоль осей 0Y и 0X.
Вторая группа — уравнения




связывают между собой компоненты Ex и Hy.
Из первого уравнения (39) следует, что переменное магнитное поле Hy порождает переменное электрическое поле Ex. В свою очередь, из второго уравнения (39) следует, что переменное электрическое поле Ex порождает переменное магнитное поле Hy. Этот процесс периодически повторяется. Поля Ey и Hx в этом случае не возникают. Векторы E и Hвзаимно перпендикулярны и направлены, соответственно, вдоль взаимно осей 0X и 0Y.
Итак, для описания плоской электромагнитной волны достаточно взять одну из независимых групп уравнений – или группу уравнений (4.38), или группу (39). При этом компоненты другой группы будут равны нулю.
Возьмем, например, группу уравнений (39). При этом выборе Ey = 0 и Hx = 0. Продифференцируем первое уравнение (39) по z, и, поменяв последовательность дифференцирования в правой части, получим:


Подставим в это уравнение второе уравнение из (39), получим:






где: c = 

Аналогично, продифференцировав второе уравнение (39) по z, и подставив в полученный результат первое уравнение, получим волновое уравнение для Hy: 



Разумеется, полученные волновые уравнения (40) и (41) являются частным случаем уравнений (32) и (33), однако случай плоской волны позволяет существенно упростить анализ свойств электромагнитной волны.
Решение волнового уравнения. Свойства электромагнитной волны. Часть свойств электромагнитной волны выяснены выше: электромагнитная волна является поперечной волной; векторыE и Hволны взаимно перпендикулярны. Для обсуждения других свойств волны рассмотрим решение волновых уравнений (40) и (41).
Напомним, решением дифференциальных уравнений вида (40) и (41) является любая непрерывная и дифференцируемая функция вида
когда волна распространяется в положительном направлении 0Z, или функция F(vt + z),
когда распространяется в отрицательном направлении 0Z.
Допустим, в источнике электромагнитных волн вектор напряженности электрического поля E совершает гармонические колебания в направлении 0Y и в пространство излучается плоская электромагнитная волна в направлении 0Z. В этом случае в качестве решения (40) и (41) естественно выбрать функцию косинуса (или синуса).
Однако аргумент функции F(vt – z) измеряется в метрах, а аргумент косинуса в радианах, поэтому необходимо умножить (vt – z) на постоянную величину, измеряемую в единице 


Ex = E0 cos [ 
Проведем анализ уравнения волны (4.42), для чего раскроем скобки в аргументе (42): E0 cos [ 


Длина волны, волновое число, период колебаний.
В фиксированный момент времени t на расстоянии между двумя точками пространства, равном l, фаза волны изменяется на полный угол 2p радиан ( 


За промежуток времени, в течение которого волна проходит расстояние равное длине волны l, электрическое поле E в фиксированной точке пространства совершает одно полное колебание. Этот промежуток времени называется периодом колебаний электрического поля: T = 


где: f = 
Воспользовавшись приведенными соотношениями, уравнение волны для электрического поля (42) можно записать в виде
Решение волнового уравнения (4.41) для магнитного поля Hy имеет аналогичное содержание:
В уравнениях волны (44) и (45) начальные фазы напряженностей Ex и Hy обозначены через j и g. Покажем, что фазы колебаний Exи Hy в любой момент времени и в каждой точке пространства одинаковы. Из уравнений (44) и (45) следует, что для этого достаточно показать равенство их начальных фаз: j = g.
Равенство фаз колебаний полейExи Hy электромагнитной волны в идеальном диэлектрике (синфазное колебание Exи Hy).
Напомним, под идеальным диэлектриком понимается среда, в которой отсутствуют свободные заряды, и которая, следовательно, не проводит электрический ток.
Уравнения (44) и (45) являются решениями волновых уравнений соответственно (40) и (41), которые, в свою очередь, получены из группы уравнений (39). Подставим (44) и (45) в (39), получим:
Эти равенства показывают, что, во-первых, фазы колебаний Exи Hy одинаковые, т.е. (wt – kz + j) = (wt – kz + g), что выполняется при равенстве начальных фаз j = g. Итак, решение волновых уравнений в диэлектрике имеют вид:
Во-вторых, должны выполняться соотношения
Перемножив эти уравнения, получим: k 



Это соотношение верно и для других мгновенных значений E и H в идеальном диэлектрике.
Величина 


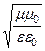
Z0 = 



На рис. 34 показаны векторы E и H гармонической электромагнитной волны в разных точках среды в некоторый фиксированный момент времени t (волна находится в идеальном диэлектрике). Пространственный профиль векторов E и H гармонической волны образуют синусоиду, которая на рисунке представлена огибающей значений векторов в объеме диэлектрика. С течением времени профиль будет смещаться в направлении оси 0Z со скоростью v = 
 |
Приведем некоторые выводы из ранее изложенного. Научные факты, выявленные в результате экспериментальных исследований явлений электромагнетизма в макромире, теоретически обобщены системой из четырех уравнений Максвелла. В свою очередь, следствия, получаемые из уравнений Максвелла, находятся в согласии с экспериментальными фактами. Часть следствий были рассмотрены выше:
1) из уравнений Максвелла следует существование электромагнитного поля, распространяющегося в виде электромагнитной волны (электромагнитного излучения) с фазовой скоростью v = 

2) электромагнитная волна – поперечная волна, причем вектора E и H взаимно перпендикулярны и образуют совместно с фазовой скоростью волны v правовинтовую систему (E ® H®v);
3) фазы колебаний Exи Hy в диэлектрике в любой момент времени в каждой точке пространства одинаковы ([1]) (векторы E и H в каждой точке пространства колеблются в фазе);
4) амплитуды векторов E и H связаны между собой соотношением 

5) волновое сопротивление диэлектрика определяется соотношением
Z0 = 
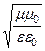

Используя понятие волнового сопротивления, решение волновых уравнений (44 * ) и (45 * ) можно представить в виде:
Hy = 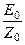
В заключение параграфа отметим, что если фазовая скорость v электромагнитной волны направлена произвольно относительно осей координат, то решение волнового уравнения — уравнение волны — определяется всеми координатами. Например, решения волновых уравнений (32) и (33) в случае плоской гармонической волны, распространяющейся в направлении, образующий с осями координат 0X, 0Y, 0Z углы a, b, h, имеют вид:E(r,t)= E0 cos (wt – kr+ g),(49)
H(r,t)= H0 cos (wt – kr+ g), (50)
где: k = 




3.5.3. Дифференциальные уравнения Максвелла в комплексной
форме
1. Представление гармонических процессов в комплексной форме. Мы уже оперировали комплексными величинами. Здесь обратим внимание еще на одну деталь, связанную с комплексным представлением электромагнитных волн.В предыдущем параграфе в качестве решения волнового уравнения выбрана гармоническая (синусоидальная) функция. В этом есть определенный резон. И дело даже не в том, что выбранное простое решение позволяет наглядно воспринимать результат и анализ решения. Большинство сигналов, используемых в акустике, электротехнике и радиотехнике, являются периодическими функциями F(t), которые могут быть разложены по гармоническим функциям в ряд Фурье (при дискретном частотном спектре) или интеграл Фурье (при непрерывном спектре частот). В этой связи, изучение гармонических электромагнитных волн важно как в познавательном плане, так и для практики.
Уравнения Максвелла в дифференциальной форме содержат производные по координатам и времени. В этой связи уравнение гармонической волны удобно представлять в комплексной форме, воспользовавшись формулой Эйлера 

Напомним, операция перехода от вещественной гармонической функции к экспоненциальной комплексной функции проводится следующим образом. Воспользовавшись вещественной функцией x(t) = A0cos (wt + j),формируется комплексная величина xк(t):
В соответствии с формулой Эйлера, функцию xк(t) записывается в виде комплексной экспоненциальной функции
xк(t) = A0 

Величина 



xк(t) = 
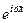
Линейные операции (сложение, дифференцирование, интегрирование и т.п.) над комплексными функциями проводятся раздельно над вещественным и мнимым частями комплексной функции. В результате таких операций вновь получается некоторая комплексная величина. От конечной комплексной функции можно выделить вещественную часть, и, тем самым, записать результат вычислений в виде вещественной синусоидальной функции.
Представим уравнение плоской волны (49) в комплексной форме:
Eк(x, y, z; t) = E0 

Eк(x, y, z; t) = 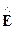

где 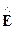

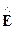
В уравнении волны (49) вещественного вектора Eпространственная и временная аргументы входят в функцию косинуса совместно, а в уравнении волны комплексной функции Eк (52) пространственная и временная аргументывходят в раздельно в разные сомножители — 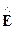

Уравнение волны комплексной векторной функцииHк(50)имеет аналогичный вид: Hк(x, y, z; t) =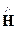

где 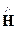

2. Уравнения Максвелла в комплексной форме. Подставим в уравнения для роторов электромагнитного поля
[Ñ, E] = — 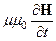

уравнения волны комплексных векторных функций Eк (52) и Hк (53). Напомним, оператор набла Ñ представляет собой дифференцирование по координатам, следовательно: [Ñ, Eк] = [Ñ,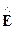

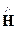


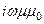

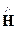




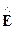

Итак,уравнения Максвелла в комплексной форме для роторов имеют вид: [Ñ, Eк] = — 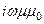

Уравнения Максвелла для комплексных амплитуд E * и H * получается после сокращения на множитель 
[Ñ,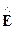
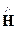
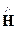
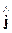

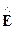
где 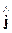
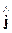

Запишем уравнения Максвелла в комплексной форме для дивергенций:
3.5.4. Граничные условия
http://pandia.ru/text/80/150/53512.php
http://megaobuchalka.ru/8/34853.html


















