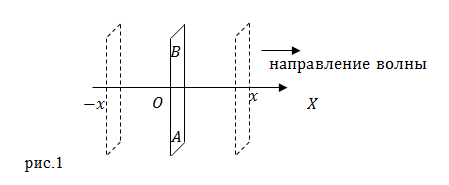
Уравнение плоской волны распространяющейся вдоль оси ох

Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.

.

(5.2.1)

Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом.

Уравнение плоской волны

Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер.

Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t: . Пусть колебание точек, лежащих в плоскости , имеет вид (при начальной фазе )

(5.2.2)

Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время .

Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости , т.е.

,

(5.2.3)

– это уравнение плоской волны.

Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания . Это будет, если энергия волны не поглощается средой.

Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z.

В общем виде уравнение плоской волны записывается так:

, или .

(5.2.4)

Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны.

Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид:

.

Уравнение волны можно записать и в другом виде.

Введем волновое число , или в векторной форме:

,

(5.2.5)

где – волновой вектор, – нормаль к волновой поверхности.

Так как , то . Отсюда . Тогда уравнение плоской волны запишется так:

.

(5.2.6)

Уравнение сферической волны

В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической.

Предположим, что фаза колебаний источника равна wt (т.е. ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону . Следовательно, уравнение сферической волны:

, или ,

(5.2.7)

где А равна амплитуде на расстоянии от источника равном единице.

Уравнение (5.2.7) неприменимо для малых r, т.к. при , амплитуда стремится к бесконечности. То, что амплитуда колебаний , следует из рассмотрения энергии, переносимой волной.

Уравнение плоской волны распространяющейся вдоль оси ох

отстоящие друг от друга на расстоянии λ, колеблются одинаковым образом.

Уравнение плоской волны

Найдем вид функции . в случае плоской волны, предполагая, что колебания носят гармонический характер.

Пусть колебание точек, лежащих в плоскости x = 0, имеет вид (при начальной фазе ф = 0)

Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время τ = х/v. Следовательно, колебания частиц в плоскости x будут отставать по времени на τ от колебаний частиц в плоскости x = 0, т. е.

— это уравнение плоской волны (рис. 2.4.3). Таким образом, . есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания A = const. Это будет, если энергия волны не поглощается средой.

Такой же вид уравнение (2.4.5) будет иметь, если колебания распространяются вдоль оси y или z.

В общем виде уравнение плоской волны записывается так:

Выражения (2.4.5) и (2.4.6) есть уравнения бегущей волны. Уравнение волны можно записать и в другом виде.

Введем волновое число k = 2π/λ, или в векторной форме

где k — волновой вектор; n — нормаль к волновой поверхности.

Так как λ = vT , то k = 2π/vT = 2πν/v = ω/v. Отсюда v = ω/k.

Тогда уравнение плоской волны запишется так:

Плоская волна

Определение и основные понятия плоской волны

Пусть источником волн в бесконечной упругой среде является бесконечно большая пластина. Она совершает колебания вдоль оси X, плоскость пластины перпендикулярна оси X (рис.1).

Пластина совершает гармонические колебания. Введем следующие обозначения: $s_0$ — смещение точек пластины AB и примыкающих к ней частиц среды от положения равновесия; $A_0$ — амплитуда колебаний пластины; $\varphi $ — фаза колебаний; $\omega $ — циклическая частота колебаний. Уравнение колебаний пластины имеет вид:

В таком случае в среде распространяется гармоническая волна такой же частоты. Если среда является однородной и изотропной, то колебания всех частиц вещества на одинаковых расстояниях от пластины идентичны (совпадают амплитуды и начальные фазы колебаний). То есть волновые поверхности имеют вид параллельных плоскостей, которые перпендикулярны оси X (направлению волны). Данные волны называют плоскими.

Волны, волновые поверхности которых представляют собой плоскости, называют плоскими.

Уравнение плоской волны

Колебания в точках среды, находящихся на расстоянии $x$ от плоскости AB отстают по фазе от колебаний источника на величину $kx$:

при отсутствии рассеяния энергии волны в веществе $A$=$A_0$. $k=\frac<2\pi ><\lambda >\ $- волновое число.

Для точек пространства находящихся правее плоскости AB $x>0$, для точек находящихся левее этой плоскости $x Пример 1

Задание: Плоская гармоническая волна распространяется по прямой, которая совпадает с осью X, в положительном направлении оси. Среда энергию не поглощает. Скорость распространения волны равна $v$. Амплитуда волны $A.$ Две точки, которые находятся на расстояниях $x_1\ и\ x_2$ от источника волны совершают колебания с разностью фаз $\Delta \varphi =\frac<3\pi ><5>$. Какова длина волны? Запишите уравнение волны.

Решение: Запишем уравнение плоской волны:

Фазы колебаний двух точек в этой волне равны:

\[<\varphi >_1=\omega t-kx_1+\varphi ;;\ <\varphi >_2=\omega t-kx_2+\varphi \left(1.3\right).\]

Найдем их разность:

\[\Delta \varphi =\omega t-kx_2+\varphi -\left(\omega t-kx_1+\varphi \right)=k\left(x_2-x_1\right)=\frac<2\pi ><\lambda >\left(x_2-x_1\right)\left(1.4\right).\]

Выразим длину волны ($\lambda $) из (1.4):

Для написания уравнения волны через известные из условий задачи величины используем формулу:

Можем записать уравнение волны:

Задание: В однородном упругом веществе имеется плоская стоячая волна вида: $s=A<\cos (\omega t)\ ><\cos (kx)\ >$. Нарисуйте графики зависимости $s\left(x\right)$ при $t=0$ и $t=\frac<2>$, где $T$ — период колебаний.