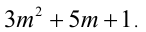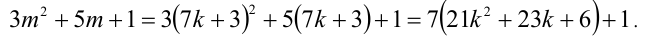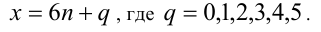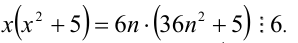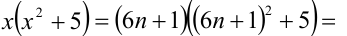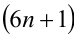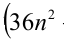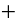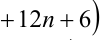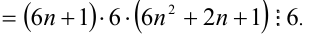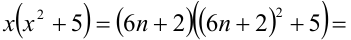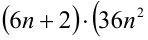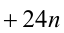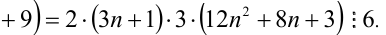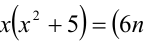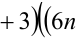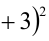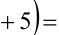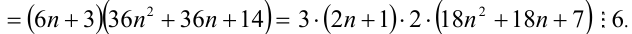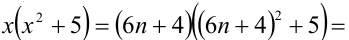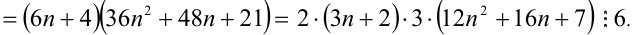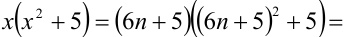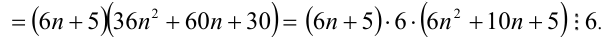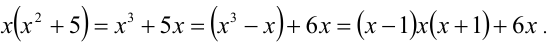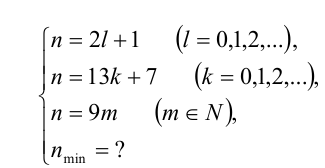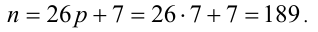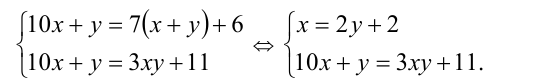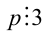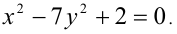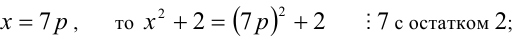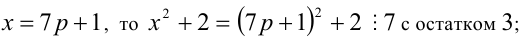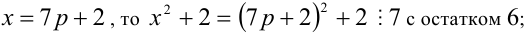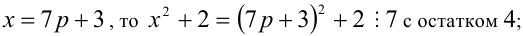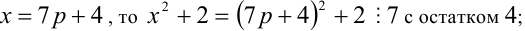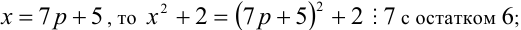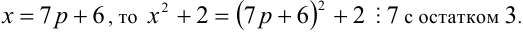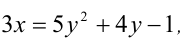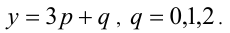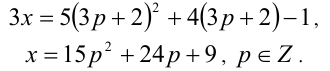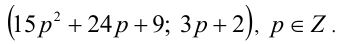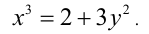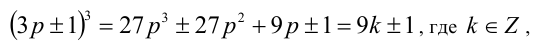Уравнение по задаче с остатком

Деление чисел с остатком

О чем эта статья:

Деление с остатком целых положительных чисел

Деление — это разбиение целого на равные части.

Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.

Теорема

a = b · q + r, где a — делимое, b — делитель, q — неполное частное, r — остаток. 0 ⩽ r

Проверка деления с остатком

Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.

Формула деления с остатком

a = b * c + d,

где a — делимое, b — делитель, c — неполное частное, d — остаток.

Эту формулу можно использовать для проверки деления с остатком.

Пример

Рассмотрим выражение: 15 : 2 = 7 (остаток 1).

В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.

Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:

Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!

Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.

Попрактикуемся в решении.

Пример

Разделить 14671 на 54.

Выполним деление столбиком:

Неполное частное равно 271, остаток — 37.

Ответ: 14671 : 54 = 271(остаток 37).

Деление с остатком положительного числа на целое отрицательное

Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:

В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.

Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.

Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».

Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.

Алгоритм деления положительного числа на целое отрицательное (с остатком):

• найти модули делимого и делителя;
• разделить модуль делимого на модуль делителя
• получить неполное частное и остаток;
• записать число противоположное полученному.

Пример

Разделить 17 на −5 с остатком.

Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.

Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.

Проверка : a = b * q + r, 17 = −5 * (−3) + 2.

Ответ: 17 : (− 5) = −3 (остаток 2).

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Деление с остатком целого отрицательного числа на целое положительное

Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:

Чтобы получить неполное частное q при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток r будет вычисляться по формуле:

r = a − b * q

Из правила делаем вывод, что при делении получается целое неотрицательное число.

Для точности решения применим алгоритм деления а на b с остатком:

• найти модули делимого и делителя;
• разделить по модулю;
• записать противоположное данному число и вычесть 1;
• использовать формулу для остатка r = a − b * q.

Рассмотрим пример, где можно применить алгоритм.

Пример

Найти неполное частное и остаток от деления −17 на 5.

Разделим заданные числа по модулю.

Получаем, что при делении частное равно 3, а остаток 2.

Так как получили 3, противоположное ему −3.

Необходимо отнять единицу: −3 − 1 = −4.

Чтобы вычислить остаток, необходимо a = −17, b = 5, q = −4, тогда:

r = a − b * q = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.

Значит, неполным частным от деления является число −4 с остатком 3.

Проверка: a = b * q + r, −17 = 5 * (−4) + 3.

Ответ: (−17) : 5 = −4 (остаток 3).

Деление с остатком целых отрицательных чисел

Сформулируем правило деления с остатком целых отрицательных чисел:

Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:

r = a − b * q

Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.

Алгоритм деления с остатком целых отрицательных чисел:

• найти модули делимого и делителя;
• разделить модуль делимого на модуль делителя;
• получить неполное частное и остаток;
• прибавить 1 к неполному частному;
• вычислить остаток, исходя из формулы r = a − b * q.

Пример

Найти неполное частное и остаток при делении −17 на −5.

Применим алгоритм для деления с остатком.

Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.

Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.

Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим r = a − b * q = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.

Получилось, что остаток равен 3, а неполное частное равно 4.

Проверка: a = b * q + r, −17 = −5 * 4 + 3.

Ответ: (−17) : (−5) = 4 (остаток 3).

Деление с остатком с помощью числового луча

Деление с остатком можно выполнить и на числовом луче.

Пример 1

Рассмотрим выражение: 10 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.

Решение: 10 : 3 = 3 (остаток 1).

Пример 2

Рассмотрим выражение: 11 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.

Метод анализа остатков

Метод анализа остатков

В основе метода анализа остатков, который используется при решении ряда задач с целочисленными неизвестными, лежит формула деления с остатком. Суть метода состоит в рассмотрении случаев различных остатков от деления на заданное число, что позволяет в конечном итоге решить поставленную задачу.

В первых трёх примерах, приведённых ниже, в явном виде ищутся остатки от деления одних целых чисел на другие.

Пример №19.

Найти частное и остаток от деления числа (— 23) на 7.

Решение:

Согласно формуле деления с остатком, получаем:

— 23 = — 4 • 7 + 5 , т.е. частное равно — 4, а остаток равен 5.

Пример №20.

Найти сумму остатков, получающихся при делении числа 7263544587435873 на 2, 4, 5, 9, 10, 25.

Решение:

Используя признаки делимости нацело на числа 2,4,5,9,10 и 25, находим остатки:

• остаток от деления на 2 равен 1;
• остаток от деления на4 равен 1;
• остаток от деления на 5 равен 3;
• остаток от деления на 9 равен 0;
• остаток от деления на 10 равен 3;
• остаток от деления на 25 равен 23.

Суммируя остатки 1 + 1+3+0+3+23, получаем в ответе 31.

Пример №21.

Пусть остаток от деления натурального числа m на 7 равен 3. Найти остаток от деления на 7 числа

Решение:

Из условия следует, что число m имеет вид: 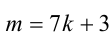. Тогда

Таким образом, остаток от деления числа 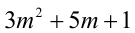на 7 равен 1.

Пример №22.

Доказать, что при любых целых X число 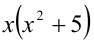делится нацело на 6.

Решение:

Разобьём множество всех целых X на 6 групп в зависимости от остатка при делении на 6, т.е. рассмотрим 6 случаев:

1) Пусть 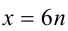, тогда

2) Пусть 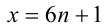, тогда

3) Пусть 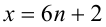, тогда

4) Пусть 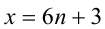, тогда

5) Пусть 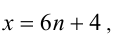тогда

6) Пусть 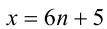, тогда

Таким образом, мы рассмотрели все целые числа X и доказали, что всегда (в каждом из шести случаев) выражение 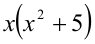кратно 6.

Замечание. Эту задачу можно было решить иначе. Преобразуем данное в условии задачи выражение:

Каждое из двух слагаемых делится нацело на 6 (первое как произведение трёх последовательных целых чисел), поэтому их сумма кратна 6.

Пример №23.

Учительница принесла в класс счётные палочки. Дети раскладывали их в пакетики. Когда разложили по 2 палочки в каждый пакетик, то осталась 1 лишняя палочка. Затем разложили по 13 штук в пакетик, и тогда осталось 7 лишних палочек. Когда же палочки разложили по 9 штук в пакетик, то лишних не осталось. Сколько, самое меньшее, было счётных палочек?

Решение:

Пусть всего было n счётных палочек. Тогда условия задачи приводят к системе

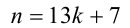
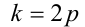
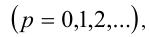
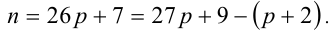
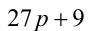
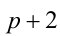
Таким образом, требуется найти наименьшее натуральное нечётное число п , делящееся на 9 и дающее при делении на 13 остаток 7. Заметим, что в силу нечётности число k должно быть чётным, т.е. причём меньшему n соответствует меньшее р , но тогда имеем Поскольку числа п и делятся нацело на 9, то, следовательно, число также должно быть кратно 9 (и при этом быть минимальным). Наименьшее целое неотрицательное р , для которого выполняются эти условия, равно 7, откуда находим

Ответ: самое меньшее — 189 счётных палочек.

Пример №24.

После деления некоторого двузначного числа на сумму его цифр получается 7 и в остатке 6. После деления этого же двузначного числа на произведение его цифр в частном получается 3 и в остатке 11. Найти это двузначное число.

Решение:

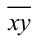
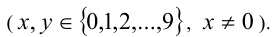
Обозначим — искомое число Тогда, по условию, имеем систему уравнений

Решая систему методом подстановки, находим единственное решение, удовлетворяющее всем условиям задачи: x= 8, y = 3 . Ответ: 83.

Пример №25.

Целые числа m, n,k не делятся нацело на 3. Доказать, что число 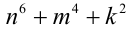делится на 3.

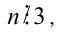
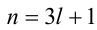
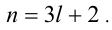
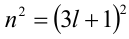
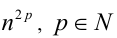
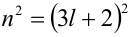
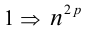
Доказательство. Если то возможны два случая: и . В первом случае — делится на 3 с остатком 1, а значит, , также делится на 3 с остатком 1. Аналогично во втором случае: делится на 3 с остатком делится на 3 с остатком 1. Таким образом, если целое число не делится нацело на 3, то его квадрат (любая чётная степень) при делении на 3 дают остаток 1. Но тогда сумма трёх таких чётных степеней кратна 3.

Пример №26.

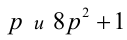
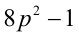
Доказать, что если — простые числа, то — тоже простое число.

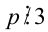
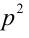
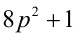
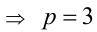
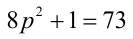
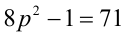
Доказательство. Если , то остаток от деления на 3 равен 1. Но тогда делилось бы на 3, что противоречит условию. Следовательно, , тогда действительно — простое число, и при этом тоже является простым.

Пример №27.

Решить уравнение в целых числах

Решение:

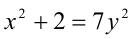
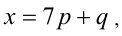
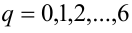
Перепишем уравнение в виде: . Заметим, что правая часть уравнения при любом целом Y делится нацело на 7. Выясним, какие остатки при делении на 7 даёт левая часть данного уравнения. Для этого разобьём множество всех целых X на 7 групп в зависимости от остатка при делении на 7: где , и рассмотрим каждый из этих случаев в отдельности.

1) Если

2) если

3) если

4) если

5) если

6) если

7) если

Итак, правая часть уравнения делится на 7 нацело (т.е. с остатком 0), а левая часть при этом — с остатками 2, 3, 4, 6. Однако равные числа при делении на одно и то же целое число 7 должны давать одинаковые остатки. Полученное противоречие говорит о том, что данное уравнение не имеет решений в целых числах.

Пример №28.

Найти все пары целых чисел (x;y), удовлетворяющие уравнению

и доказать, что для каждой такой пары сумма 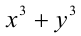является нечётным числом.

Решение:

Заметим, что левая часть уравнения кратна 3, следовательно, и правая часть должна делиться на 3 нацело. Разобьём множество всех целых y на три группы в зависимости от остатка при делении на 3:

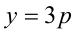
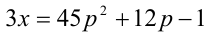
1) Если , то уравнение примет вид . Это равенство невозможно, так как его левая часть кратна 3, а правая — нет.

2) Если 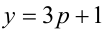, то получим аналогичную ситуацию.

3) Наконец, если 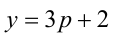, то, подставляя в уравнение, получим

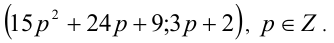
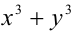
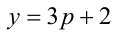
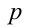
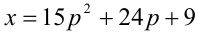
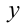
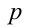
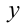
Следовательно, общий вид решений:Осталось показать, что — нечётно. В самом деле, если чётно, то — чётно и, значит, — нечётно. Если, наоборот, — нечётно, то также нечётно, а значит, — чётно. Таким образом, числа и , а значит и их кубы, имеют всегда разную чётность, поэтому их сумма есть нечётное число.

Ответ:

Пример №29.

Решить в целых числах уравнение

Решение:

Так как произвольное целое число представимо в виде , или где , а

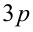
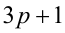
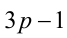
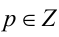
то любое число в кубе или делится нацело на 9, или даёт при делении на 9 в остатке 1 или 8. Аналогично, так как 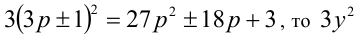даёт при делении на 9 остаток 0 или 3. Итак, правая часть уравнения может делиться на 9 с остатками 2 или 5, а левая — 0, 1 или 8. Следовательно, уравнение не имеет решений в целых числах.

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Контрольная работа «Решение задач и уравнений.Деление с остатком.»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Контрольная работа 7 «Решение задач и уравнений. Деление с остатком.»

Школьники собрали 12 корзинок ягод, по 8 килограммов в каждой корзинке. После того, как часть ягод отправили в детский сад, осталось 25 килограммов ягод. Сколько килограммов ягод отправили в детский сад ?

Примеры 2 . Выполни деление с остатком и сделай проверку.

48:10 50:15 53:8 68:9

63: (24 – 17) 24*4 -48

6*8: 3 ( 27 + 24) : 17

19 * Х = 76 57: Х =3

5. 4м 26см =…см 706см = .м . см

8см 4мм= …мм 73 дм = . м . дм

В школьный буфет привезли 14 ящиков печенья по 7 килограммов в каждом ящике. После того как продали часть печенья, осталось 29 килограммов. Сколько килограммов печенья продали?

Примеры 2 Выполни деление с остатком и сделай проверку.

56:10 60:25 51:7 69:8

( 30 -12) : 6 26*3 — 39

7*8: 3 ( 29 + 39) : 17

17 * Х = 80 54: Х =3

5. 7м 51см =…см 905см = .м . см

4см 9мм= …мм 64 дм = . м . дм

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 925 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 684 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 578 515 материалов в базе

Материал подходит для УМК

«Математика (в 2 частях)», Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 06.03.2018
• 9558
• 2128

• 06.03.2018
• 488
• 2

• 06.03.2018
• 528
• 2

• 06.03.2018
• 343
• 0

• 06.03.2018
• 694
• 0

• 05.03.2018
• 757
• 1

• 05.03.2018
• 296
• 3

• 05.03.2018
• 515
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 06.03.2018 4141
• DOCX 13.6 кбайт
• 130 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Коваленко Елена Анатольевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 3 года и 11 месяцев
• Подписчики: 0
• Всего просмотров: 64087
• Всего материалов: 36

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Онлайн-конференция о создании школьных служб примирения

Время чтения: 3 минуты

Приемная кампания в вузах начнется 20 июня

Время чтения: 1 минута

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.