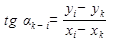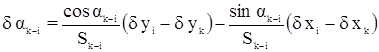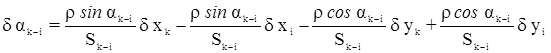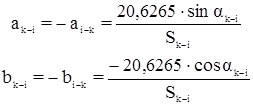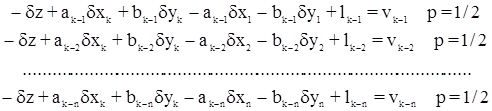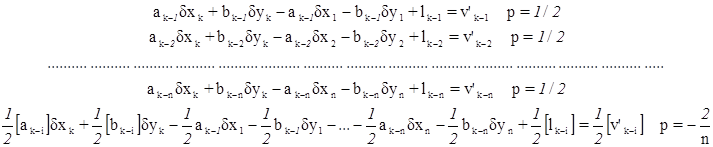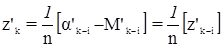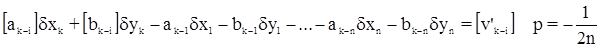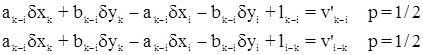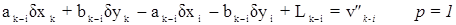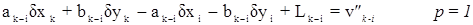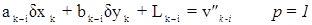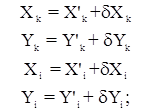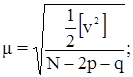Уравнение погрешности и расчет ошибок

Составление уравнений погрешностей

Вывод уравнений погрешностей при уравнивании триангуляции по направлениям сводится к установлению зависимости между поправками координат и поправками измеренных направлений. Ранее после дифференцирования уравнения

.

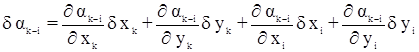
Дифференцируя исходное уравнений tg a = f (x, y) получим:

.

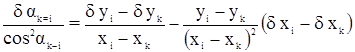
Для получения d a_k—i в секундах необходимо правую часть уравнения умножить на r”. Если S_k—i выражено в километрах, то для получения d x и d y в дециметрах в уравнении

принимаем r = 20,6265”.

В этом уравнении пункты k и i являются определяемыми. Т.к. поправки в исходные координаты не вводятся, то если пункт і является исходным, то:

Если оба пункта являются исходными, то d a_k—i = 0.

Таким образом, мы получили так называемые непреобразованные уравнения погрешностей, в которых неизвестными являются поправки d x и d y к приближенным значениям координат x’ и y’ определяемых пунктов и ориентирные поправки d z:

1. измеренному направлению с исходного пункта k на исходный пункт i соответствует уравнение:

2. измеренному направлению с определяемого пункта k на исходный пункт i соответствует уравнение:

Направлению с исходного пункта i на определяемый пункт k соответствует уравнение:

3. измеренному направлению с определяемого пункта k на определяемый пункт i соответствует уравнение:

Веса всех преобразованных уравнений погрешностей равны между собой, т.е. направления измерены равноточно. Число уравнений погрешностей равно общему числу измеренных направлений, включая и направления между исходными пунктами. Число неизвестных равно 2 р + q, где р – количество определяемых пунктов; q – количество отнаблюденных пунктов, равное числу поправок d z.

При уравнивании триангуляции по углам уравнения погрешностей получают как разности из уравнений для соответствующих направлений. Например, в пункте k между направлениями на пункты i и j имеем уравнения погрешностей для направлений:

При этом число уравнений погрешностей равно числу измеренных углов, а число неизвестных – удвоенному числу определяемых пунктов.

9.5 Преобразование уравнений погрешностей

Для упрощения вычислений непреобразованные уравнений погрешностей (т.е. уравнения с ориентирными поправками dz) преобразовывают на основании теории эквивалентных уравнений. Эти преобразования позволяют сократить число уравнений погрешностей и число входящих в них неизвестных.

9.5.1 Исключение ориентирных поправок.

Вес измеренного направления (непреобразованного уравнения погрешностей) примем равным ½. Для каждого наблюдаемого пункта записывают группу уравнений с общеориентирной поправкой dz.

Если один или несколько пунктов являются исходными, то поправки в координаты этих пунктов равны нулю. На основании 1-го правила Шрейбера исключаем ориентирную поправку dz из п уравнений, заменив ее эквивалентной системой п+1 уравнений:

В этой системе уравнений поправки v’_k—i уже не являются поправками к измеренным направлениям, а численно равны v’_k—i = v_k—i + dz_k. Учитывая, что

и [l_k—i] = 0, на основании третьего положения теории эквивалентных уравнений последнее суммарное уравнение заменим на уравнение

Аналогично преобразовывают уравнения погрешностей на остальных наблюдаемых пунктах.

9.5.2 Сложение уравнений взаимных направлений.

Для стороны сети триангуляции между определяемыми пунктами k и i в случае двустороннего визирования после исключения ориентирных поправок получим два уравнения, которые отличаются только свободными членами:

На основании второго положения теории эквивалентных уравнений эти уравнения могут быть заменены одним уравнением:

где .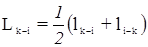

9.5.3 Приведение уравнений погрешностей к весу, равному 1.

Теперь только уравнения для сторон с односторонним визированием и суммарные уравнения будут иметь веса, не равные 1. Их можно привести к весам, равным 1 или –1. Согласно третьему положению теории эквивалентных уравнений такие уравнения можно заменить на эквивалентные с весом 1 или –1.

с весом р = 1.

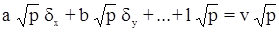
9.6 Составление преобразованных уравнений погрешностей

На основании правил составления эквивалентных уравнений погрешностей можно сформулировать правила составления преобразованных уравнений погрешностей:

1-е правило. Стороне сети между определяемыми пунктами k и i соответствует уравнение погрешностей:

а) в случае двустороннего визирования:

б) в случае одностороннего визирования с пункта k на пункт i:

.

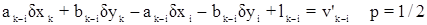
2-е правило.Стороне сети между определяемым пунктом k и исходным пунктом i соответствует уравнение погрешностей:

а) в случае двустороннего визирования:

б) в случае одностороннего визирования с пункта k на пункт i:

.

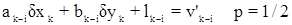
3-е правило. Каждому отнаблюденному пункту k отвечает суммарное уравнение с отрицательным весом:

При этом на исходном пункте k в суммарных уравнениях отсутствуют два первых слагаемых с коэффициентами [a_k—i] и [b_k—i].

Общее число уравнений погрешностей равно числу сторон в сети (не считая сторон между исходными пунктами) плюс общее число отнаблюденных пунктов. В преобразованных уравнениях погрешностей неизвестными являются поправки в координаты определяемых пунктов. Количество неизвестных равно удвоенному числу определяемых пунктов.

9.7 Последовательность и контроль уравнительных вычислений

2. вычисление предварительных координат определяемых пунктов Х’_опр, Y’_опр;

4. составление уравнений погрешностей;

5. составление и решение нормальных уравнений;

6. вычисление уравненных значений:

,

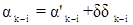
dz_k = .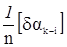

7. выполнение контрольных вычислений. Кроме того, для контроля a_k—i вычисляют по уравненным координатам точек:

.

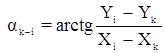
8. оценка точности уравненных элементов сети. При весе измеренных направлений р = ½ средняя квадратическая погрешность единицы веса равна:

где N – число измеренных направлений (включая и между исходными пунктами);

р – число определяемых пунктов;

q – число отнаблюденных пунктов.

СКП измеренного направления:

.

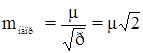
СКП измеренного угла:

.

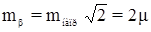
СКП положения пункта:

,

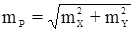
где ;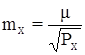

.

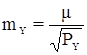
Дата добавления: 2016-06-02 ; просмотров: 1456 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Оценка погрешности прямых измерений

Вычисляет погрешность прямых измерений для заданной выборки и доверительного интервала.

Измеряя линей­ные размеры предметов измерительными инстру­ментами : линейкой, штангенциркулем, микрометром, проводя измерения времени секундомером или силы электрического тока или величины напряжения соответствующими электроизмерительными приборами Вы проводите прямые измерения.

Погрешность измерений

Любое измерение проводится с определенной точностью, при этом измеренное значение всегда отличается от истинного, так как инструменты измерения, методики и органы чувств человека несовершенны. Поэтому важную роль играет оценка погрешности измерений, результат измерений с учетом погрешности записывается в виде: X ± ΔX, где ΔX — абсолютная погрешность измерений.

Случайные и систематичес­кие погрешности

Погрешности подразделяются на случайные и систематичес­кие.
Систематические погрешности остаются постоянными или закономерно меняются в процессе измерения. Например неточность прибора, неправильная его регулировка ведет к систематической погрешности. Если причина систематической погрешности известна, то чаще всего такую погрешность можно исключить.
Случайные погрешности вызваны различными случайными факторами, влияющими на точность измерений. Например, при измерении секундомером отрезков времени, случайные погрешности связаны с различным (случайным) временем реакции экспериментатора на события запускающие и останавливающие секундомер. Чтобы уменьшить влияние случайной погрешности необходимо проводить многократное измерение физической величины.
Калькулятор ниже вычисляет случайную погрешность выборки прямых измерений для заданного доверительного интервала. Немного теории можно найти сразу за калькулятором.

Расчет погрешностей непосредственных измерений.

Измерения

Измерения

Импортировать данные Ошибка импорта

В большинстве случаев результат измерения подчиняется нормальному закону распределения, поэтому истинное значение измерения будет равно пределу:

В случае ограниченного количества измерений, наиболее близким к истинному будет среднее арифметическое:

Согласно элементарной теории ошибок Гаусса случайную погрешность отдельного измерения характеризует так называемое среднеквадратическое отклонение:
, квадрат этой величины называется дисперсией. При увеличении этой величины возрастает разброс результатов измерений, т. е. увеличивается погрешность.

Для оценки погрешности всей серии измерений, вместо отдельного измерения надо найти среднюю квадратичную погрешность среднего арифметического, характеризующую отклонение от истинного значения искомой величины .
По закону сложения ошибок среднее арифметическое имеет меньшую ошибку, чем результат каждого отдельного измерения. Cред­няя квадратичная погрешность среднего арифметического равна:

Стандартная случайная погрешность Δх равна:
, где — коэффициент Стьюдента для заданной доверительной вероятности и числа степеней свободы k = n-1.
Коэффициент Стьюдента можно получить по таблице или воспользоваться нашим калькулятором для вычисления квантилей распределения Стьюдента: Квантильная функция распределения Стьюдента. Следует иметь в виду, что квантильная функция выдает значения одностороннего критерия Стьюдента. Значение двустороннего квантиля для заданной доверительно вероятности соответствует значению одностороннего квантиля для вероятности:

Расчет погрешности измерений

3.1 Среднеарифметическая погрешность.Как уже отмечалось раньше, измерения принципиально не могут быть абсолютно точными. Поэтому в ходе измерения возникает задача об определении интервала, в котором вероятнее всего находится истинное значение измеряемой величины. Такой интервал указывают в виде абсолютной ошибки измерения.

Если предположить, что грубые промахи в измерениях устранены, а систематические ошибки сведены к минимуму тщательной настройкой приборов и всей установки и не являются определяющими, то результаты измерений будут, в основном, содержать только случайные погрешности, которые являются знакопеременными величинами. Поэтому, если проведено несколько повторных измерений одной и той же величины, то наиболее вероятным значением измеряемой величины является ее среднеарифметическое значение:

(1)

где a_i, — значение отдельных измерений, n — число проведенных измерений.

Погрешностью или абсолютной ошибкой отдельного измерения называют разность между значением, полученным в данном измерении, и среднеарифметическим значением измеряемой величины:

(2)

Средней абсолютной ошибкойназывается среднеарифметическое модулей абсолютных ошибок отдельных измерений:

(3)

При достаточно большом числе измерений случайные ошибки возникают с равной вероятностью как в сторону увеличения, так и в сторону уменьшения измеряемой величины, то есть можно считать, что истинное значение измеряемой величины заключено в интервале

(4)

Последнее неравенство обычно принято записывать как окончательный результат измерения следующим образом:

(5)

где абсолютная погрешность a_ср должна вычисляться (округляться) с точностью до одной-двух значащих цифр. Абсолютная ошибка показывает, в каком знаке числа содержатся неточности, поэтому в выражении для а_ср оставляют все верные цифры и одну сомнительную. То есть среднее значение и средняя ошибка измеряемой величины должны вычисляться до цифры одного и того же разряда. Например: g = (9,78 ± 0,24) м/с 2 .

Относительная погрешность.Абсолютная ошибка определяет интервал наиболее вероятных значений измеряемой величины, но не характеризует степень точности произведенных измерений. Например, расстояние между населенными пунктами, измеренное с точностью до нескольких метров, можно отнести к весьма точным измерениям, в то время как измерение диаметра проволоки с точностью до 1 мм, в большинстве случаев будет являться весьма приближенным измерением.

Степень точности проведенных измерений характеризует относительная погрешность.

Средней относительной погрешностьюили просто относительной ошибкой измерения называется отношение средней абсолютной ошибки измерения к среднему значению измеряемой величины:

(6)

или выраженная в процентах

(7)

Относительная ошибка является безразмерной величиной и обычно выражается в процентах.

3.2 Погрешность метода или приборная погрешность.Среднеарифметическое значение измеряемой величины тем ближе к истинному, чем больше проведено измерений, при этом абсолютная погрешность измерения с увеличением их числа стремится к значению, которое определяется методом измерения и техническими характеристиками используемых приборов.

Погрешность методаили приборную погрешность можно рассчитать по одноразовому измерению, зная класс точности прибора или другие данные технического паспорта прибора, в котором указывается либо класс точности прибора, либо его абсолютная или относительная погрешность измерения.

Класс точностиприбора выражает в процентах номинальную относительную ошибку прибора, то есть относительную ошибку измерения, когда измеряемая величина равна предельному для данного прибора значению

(8)

Класс точности указывается на шкале прибора цифрой, обведенной кружочком. Согласно ГОСТу все электроизмерительные приборы разделяются на 8 классов: 0,05; 0,1; 0,2; 0,5; 1.0 1,5; 2,5; 4,0.

Абсолютная погрешность прибора равна предельному для данного прибора значению измеряемой величины, умноженному на класс точности (К) и разделен­ному на 100:

(9)

Абсолютная погрешность прибора не зависит от значения измеряемой величины.

Относительная погрешность прибора (по определению):

(10)

откуда видно, что относительная приборная ошибка тем меньше, чем ближе значение измеряемой величины к пределу измерения данного прибора. Поэтому ре­комендуется подбирать приборы так, чтобы измеряемая величина составляла 60 -90% от величины, на которую рассчитан прибор. При работе с многопредельными приборами тоже следует стремиться к тому, чтобы отсчет производился во второй половине шкалы.

При работе с простыми приборами (линейка, мензурка и т.п.), классы точности и погрешности которых не определены техническими характеристиками, абсолютную погрешность прямых измерений принимают равной половине цены деления данного прибора. (Ценой деления называют значение измеряемой величины при показаниях прибора в одно деление).

Приборную погрешность косвенных измеренийможно рассчитать, используя правила приближенных вычислений. В основе вычисления погрешности косвенных измерений лежат два условия (предположения):

1. Абсолютные ошибки измерений всегда очень малы по сравнению с измеряемыми величинами. Поэтому абсолютные ошибки (в теории) можно рассматривать как бесконечно малые приращения измеряемых величин, и они могут быть заменены соответствующими дифференциалами.

2. Если физическая величина, которую определяют косвенным путем, является функцией одной или нескольких непосредственно измеряемых величин, то абсолютная ошибка функции, обусловленная бесконечно малыми приращениями, является также бесконечно малой величиной.

При указанных допущениях абсолютную и относительную погрешность можно рассчитать, используя известные выражения из теории дифференциального исчисления функций многих переменных:

	(11)
	(12)

Абсолютные ошибки непосредственных измерений могут иметь знаки «плюс» или «минус», но какой именно — неизвестно. Поэтому при определении погрешностей рассматривается наиболее невыгодный случай, когда ошибки прямых изме­рений отдельных величин имеют один и тот же знак, то есть абсолютная ошибка имеет максимальное значение. Поэтому при расчете приращений функции f(x₁ ,x₂ ,…,х_n) по формулам (11) и (12) частные приращения должны складываться по абсолютной величине. Таким образом, используя приближение Dх_i ≈ dx_i, и вы­ражения (11) и (12), для бесконечно малых приращений Dа можно записать:

	(13)
	(14)

Здесь: а — косвенно измеряемая физическая величина, то есть определяемая по расчетной формуле, Dа — абсолютная ошибка ее измерения, х₁, х₂. х_n; Dх_1, Dx₂. Dх_n, — физические величины прямых измерений и их абсолютные ошибки соответственно.

Таким образом: а) абсолютная ошибка косвенного метода измерения равна сумме модулей произведений частных производных функции измерения и соответствующих абсолютных ошибок прямых измерений; б) относительная ошибка косвенного метода измерения равна сумме модулей дифференциалов от логарифма натурального функции измерения, определяемой расчетной формулой.

Выражения (13) и (14) позволяют рассчитать абсолютные и относительные погрешности по одноразовому измерению. Заметим, что для сокращения расчетов по указанным формулам достаточно рассчитать одну из погрешностей (абсолютную или относительную), а другую рассчитать, используя простую связь между ними:

(15)

На практике чаще пользуются формулой (13), так как при логарифмировании расчетной формулы произведения различных величин преобразуются в соответствующие суммы, а степенные и показательные функции преобразуются в произведения, что намного упрощает процесс дифференцирования.

Для практического руководства по расчету погрешности косвенного метода измерения можно пользоваться следующим правилом:

Чтобы вычислить относительную ошибку косвенного метода измерения, нужно:

1. Определить абсолютные ошибки (приборные или средние) прямых измерений.

2. Прологарифмировать расчетную (рабочую) формулу.

3. Принимая величины прямых измерений за независимые переменные, найти полный дифференциал от полученного выражения.

4. Сложить все частные дифференциалы по абсолютной величине, заменив в них дифференциалы переменных соответствующими абсолютными ошибками прямых измерений.

5. Используя полученное выражение, рассчитать относительную погрешность.

6. По формуле (15) рассчитать абсолютную ошибку.

Например, плотность тела цилиндрической формы вычисляется по формуле:

(16)

где m, D, h — измеряемые величины.

Получим формулу для расчета погрешностей.

1. Исходя из используемого оборудования, определяем абсолютные погрешности измерения массы, диаметра и высоты цилиндра (∆m, ∆D, ∆h соответственно).

2. Логарифмируем выражение (16):

4. Заменяя дифференциал независимых переменных на абсолютные ошибки и складывая модули частных приращений, получаем:

5. Используя численные значения m, D, h, D, m, h, рассчитываем Е.

6. Вычисляем абсолютную ошибку

где r рассчитано по формуле (16).

Предлагаем самим убедиться, что в случае полого цилиндра или трубки с внутренним диаметром D₁ и внешним диаметром D₂

К расчету ошибки метода измерения (прямого или косвенного) приходится прибегать в случаях, когда многократные измерения либо невозможно провести в одних и тех же условиях, либо они занимают много времени.

Если определение погрешности измерения является принципиальной задачей, то обычно измерения проводят многократно и вычисляют и среднеарифметическую погрешность и погрешность метода (приборную погрешность). В окончательном результате указывают большую из них.

О точности вычислений

Ошибка результата определяется не только неточностями измерений но и неточностями вычислений. Вычисления необходимо проводить так, чтобы их ошибка была на порядок меньше ошибки результата измерений. Для этого вспомним правила математического действия с приближёнными числами.

Результаты измерений – приближённые числа. В приближённом числе все цифры должны быть верными. Последней верной цифрой приближённого числа считается такая цифра, ошибка в которой не превышает одной единицы её разряда. Все цифры от 1 до 9 и 0, если он стоит в середине или в конце числа, называются значащими. В числе 2330 — 4 значащих цифры, а в числе 6,1×10 2 – только две, в числе 0,0503 – три, так как нули слева от пятёрки незначащие. Запись числа 2,39 означает, что верны все знаки до второго после запятой, а запись в 1,2800 – что верно также и третий и четвёртый знаки. В числе 1,90 три значащих цифры и это значит, что при измерении мы учитывали не только единицы, но и десятые и сотые, а в числе 1,9 – только две значащих цифры и это значит, что мы учитывали целые и десятые и точность этого числа в 10 раз меньше.

Правила округления чисел

При округлении оставляют лишь верные знаки, остальные отбрасываются.

1. Округление достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше, чем 5.

2. Если первая из отбрасываемых цифр больше, чем 5, то последняя цифра увеличивается на единицу. Последняя цифра увеличивается также и в том случае, когда первая из отбрасываемых цифр 5, а за ней есть одна или несколько цифр, отличных от нуля.

Например, различные округления числа 35,856 будут: 35,9; 36.

3. Если отбрасываемая цифра 5, а за ней нет значащих цифр, то округление производится на ближайшее чётное число, то есть, последняя сохраняемая цифра остаётся неизменной, если она чётная и увеличивается на единицу, если она нечётная.

Например, 0,435 округляем до 0,44; 0,365 округляем до 0,36.