Показательные уравнения и неравенства
Решение большинства математических задач так или иначе связано с преобразованием числовых, алгебраических или функциональных выражений. Сказанное в особенности относится к решению показательных уравнений и неравенств. В вариантах ЕГЭ по математике к такому типу задач относится, в частности, задача C3. Научиться решать задания C3 важно не только с целью успешной сдачи ЕГЭ, но и по той причине, что это умение пригодится при изучении курса математики в высшей школе.
Выполняя задания C3, приходится решать различные виды уравнений и неравенств. Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике «Методическая копилка репетитора по физике и математике» в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.
Прежде чем приступить к разбору конкретных показательных уравнений и неравенств, как репетитор по математике, предлагаю вам освежить в памяти некоторый теоретический материал, который нам понадобится.
Показательная функция
Что такое показательная функция?
Функцию вида y = a x , где a > 0 и a ≠ 1, называют показательной функцией.
Основные свойства показательной функции y = a x :
| Свойство | a > 1 | 0 только в показателях каких-либо степеней. Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему: Помимо этого, полезно помнить об основных формулах и действиях со степенями:
Пример 1. Решите уравнение: Решение: используем приведенные выше формулы и подстановку: Уравнение тогда принимает вид: Дискриминант полученного квадратного уравнения положителен:
Это означает, что данное уравнение имеет два корня. Находим их: Переходя к обратной подстановке, получаем: Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе: С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию. Ответ: x = 3. Пример 2. Решите уравнение: Решение: ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 9 4 -x положительна и не равна нулю). Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней: Последний переход был осуществлен в соответствии с теоремой 1. Пример 3. Решите уравнение: Решение: обе части исходного уравнения можно поделить на 0,2 x . Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид: Ответ: x = 0. Пример 4. Решите уравнение: Решение: упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней: Деление обеих частей уравнения на 4 x , как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x. Ответ: x = 0. Пример 5. Решите уравнение: Решение: функция y = 3 x , стоящая в левой части уравнения, является возрастающей. Функция y = —x-2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет. Ответ: x = -1. Пример 6. Решите уравнение: Решение: упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи: Ответ: x = 2. Решение показательных неравенствПоказательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней. Для решения показательных неравенств требуется знание следующей теоремы: Теорема 2. Если a > 1, то неравенство a f(x) > a g(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 f(x) > a g(x) равносильно неравенству противоположного смысла: f(x) 2x , при этом (в силу положительности функции y = 3 2x ) знак неравенства не изменится: Тогда неравенство примет вид: Итак, решением неравенства является промежуток: переходя к обратной подстановке, получаем: Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству: Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству: Итак, окончательно получаем ответ: Пример 8. Решите неравенство: Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде: Введем новую переменную: С учетом этой подстановки неравенство принимает вид: Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство: Итак, неравенству удовлетворяют следующие значения переменной t: Тогда, переходя к обратной подстановке, получаем: Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству: Окончательно получаем ответ: Пример 9. Решите неравенство: Решение: Делим обе части неравенства на выражение: Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем: Воспользуемся заменой переменной: Исходное уравнение тогда принимает вид: Итак, неравенству удовлетворяют значения t, находящиеся в промежутке: Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая: Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе: Поскольку основание степени в данном случае оказалось меньше единицы, но больше нуля, равносильным (по теореме 2) будет переход к следующему неравенству: Итак, окончательный ответ: Пример 10. Решите неравенство: Решение: Ветви параболы y = 2x+2-x 2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине: Ветви параболы y = x 2 -2x+2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине: Вместе с этим ограниченной снизу оказывается и функция y = 3 x 2 -2x+2 , стоящая в правой части уравнения. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1. Ответ: x = 1. Для того, чтобы научиться решать показательные уравнения и неравенства, необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе, а также индивидуальные занятия с профессиональным репетитором. Искренне желаю вам успехов в подготовке и блестящих результатов на экзамене. P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно. Показательная функция, ее свойства. Простейшие показательные уравненияЭтот видеоурок доступен по абонементуУ вас уже есть абонемент? Войти На данном уроке мы рассмотрим показательную функцию, ее график и основные свойства. Также научимся решать простейшие показательные уравнения. Если у вас возникнет сложность в понимании тему, рекомендуем посмотреть урок «Показательная функция и логарифм» Открытый урок по теме «Показательная функция. Функционально-графические методы решений уравнений и неравенств»Разделы: Математика Цель: рассмотреть задачи Единого государственного экзамена базового, повышенного и высокого уровня сложности с применением функционально- графических методов на примере показательной функции у = а х , а>1, а Задачи урока:
Оборудование: презентация графиков функций, подготовленная с применением графической программы “Advanced Grapher”. 1. Вступительное слово учителя. Слайд 0. Показательная функция. “Функционально — графические методы решения уравнений и неравенств” Функционально — графический метод основан на использовании графических иллюстраций, применении свойств функции и позволяет решать многие задачи математики. Сегодня мы рассмотрим задачи Единого государственного экзамена базового, повышенного и высокого уровня сложности с применением функционально- графических методов на примере показательной функции у = а х , а>1, а Слайд 0а. Почему так важно знать свойства показательной функции?.
2. Актуализация знаний учащихся. На первом этапе урока устно по готовым чертежам повторим свойства показательной функции:
Слайд 1. Определить вид графика (устная работа 5 минут). На рисунке изображены графики показательных функций. Соотнесите график функции с формулой.
Слайд 2. Свойство монотонности показательной функции (устная работа 2 минуты). Назовите функцию, возрастающую (убывающую) на множестве действительных чисел. Соотнесите график с соответствующей формулой
При 1 0 показательная функция убывает. Слайд 3. Свойство ограниченности показательной функции (устная работа 2 минуты). Укажите множество значений функции.
Графические методы дают возможность решать неравенства, содержащие разные функции. Слайд 4. Решить графически неравенство. Что можно сказать про графики функций (График показательной функции лежит выше функции, записанной в правой части уравнения).
Рисунок8. Рисунок9. 2. Показательная функция содержит знак модуля в показателе степени. Группа В – это комбинированные задачи. Рассмотрим задачи, содержащие абсолютную величину (модуль). Повторим определение модуля.
Слайд 5. Укажите множество значений функции (5 минут). Сделать записи в тетради: 1). 2). Графическая иллюстрация представлена на слайде 5. Объяснить, как построены графики. Рисунок10. 3. Нахождение области значений сложной функции. Достаточно непросто определять область значений сложных функций. Определим, что такое сложная функция. Если функция f ставит в соответствие числу х число у, а функция g – числу у число z, то говорят что h есть сложная функция, составленная из функции g и f и пишут h=g(f(x)). При этом D(h) является E(f) или его частью D(h) Слайд 7. Используя умение строить график квадратичной функции, определите последовательно координаты вершины параболы, найдите область значений.
Вопрос: определите характер монотонности функции. Показательная функция у = 16 t возрастает, так как 16>1 . При наименьшем значении показателя функции
Е(у)=[2; График иллюстрирует наш вывод. Вопрос: определите характер монотонности функции. Показательная функция у = 3t (3t 2 -6t) + 9t – 5 = p. Введем функцию f(t) = 9t 3 -18t 2 + 9t – 5. Исследуем функцию с помощью производной и построим ее график. f ‘(x) =27t 2 – 36t + 9. Найдем стационарные точки: f ‘(x)=0. 27t 2 – 36t + 9 = 0. t1=1, t2= f( График функции f(t) = 9t 3 -18t 2 + 9t – 5 изображен на рисунке. Уравнение имеет 1 корень при р = -5 и р> Графическая иллюстрация решения выполнена с использованием программы “Advanced Grapher”. 1). 2). 3).Найдите все значения р, при которых уравнение 6. Самостоятельная работа (при наличии времени). Решить графически неравенство. 1). 2). По мере изучения курса алгебры постоянно возрастает применение функционально-графических методов, что позволяет быстро и красиво решать многие уравнения и неравенства Единого Государственного экзамена. источники: http://interneturok.ru/lesson/algebra/11-klass/pokazatelnaya-i-logarifmicheskaya-funktsii/pokazatelnaya-funktsiya-ee-svoystva-prosteyshie-pokazatelnye-uravneniya http://urok.1sept.ru/articles/511934 |
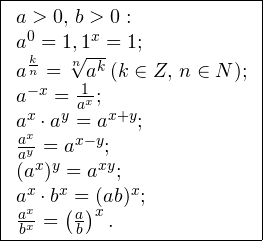 0,\, b>0: \\ a^0 = 1, 1^x = 1; \\ a^<\frac
0,\, b>0: \\ a^0 = 1, 1^x = 1; \\ a^<\frac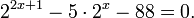
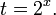
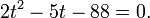
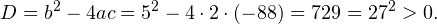 0. \]» title=»Rendered by QuickLaTeX.com»/>
0. \]» title=»Rendered by QuickLaTeX.com»/>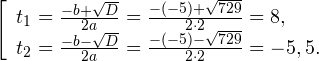
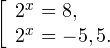
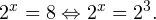
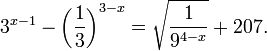
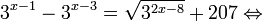
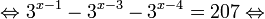
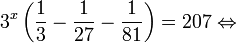
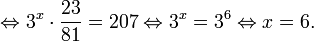
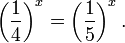
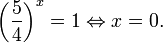
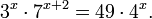
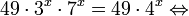
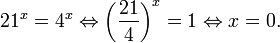
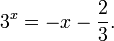

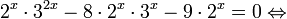
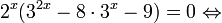
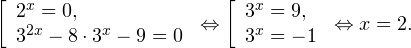
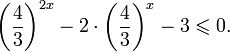
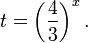
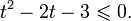
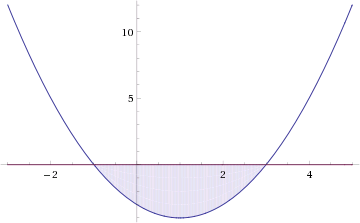
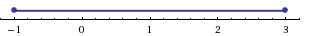
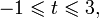
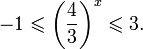
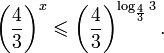
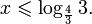
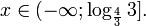
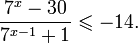
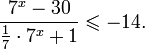
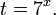
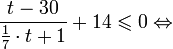
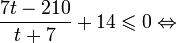
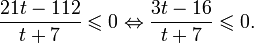

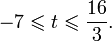
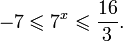

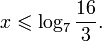
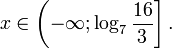
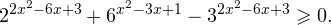
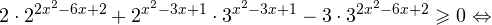
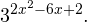
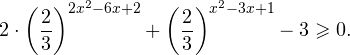
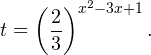
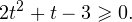
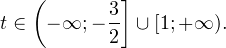
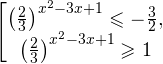
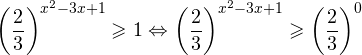
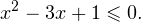
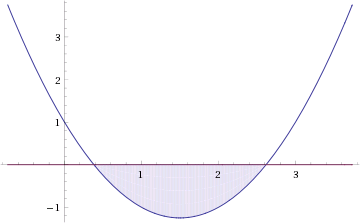
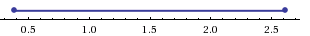
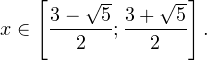
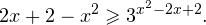
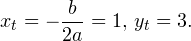
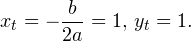

 0.
0.













 и график функции у=12 — 1,5х?
и график функции у=12 — 1,5х? >12 — 1,5х
>12 — 1,5х


 (запись на доске)
(запись на доске)






 E(f).
E(f). ,
,  — вершина параболы.
— вершина параболы.



 .
.

 убывает, так как
убывает, так как  х =t, t>0.
х =t, t>0. .
.
 )=9
)=9 =
= -2+3-5=
-2+3-5= ,
, .
.




 имеет ровно два корня.
имеет ровно два корня. . Ответ: (-
. Ответ: (- ;2].
;2]. . Ответ: (-1;0)
. Ответ: (-1;0)