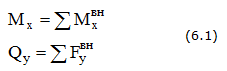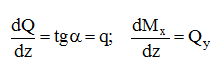Уравнение поперечной силы для сечения

Построение эпюр поперечной силы и изгибающего момента для балок. Часть 2

Построить эпюры Q_y и М_х для простой консоли, изображенной на рисунке.

1. Определение опорных реакций. Составляем уравнения равновесия:

, M_A + F.a + M — q . 2a . 4a = 0,

, R_A = q . 2a — F = qa.

2. Построение эпюр поперечной силы и изгибающего момента.

Э п ю р а Q_y. В сечении А имеем Q_A = R_A (скачок на величину и в направлении реакции R_A = qa). На участке АВ погонной нагрузки нет, поэтому поперечная сила постоянна. В сечении В поперечная сила меняется скачком от Q_BA = Q_A = qa до Q_BC = Q_BA + F = 2qa (скачок на величину и в направлении силы F = qa). На участках ВС и CD поперечная сила опять сохраняет постоянное значение, т.е. Q_BC = Q_CD = 2qa. На участке DE поперечная сила изменяется по линейному закону от Q_D = 2qa до Q_E = Q_D — q . 2a = 0.

Э п ю р а М_х. В сечении А приложен момент М_А, вызывающий растяжение верхних волокон, поэтому на эпюре изгибающего момента происходит скачок вверх на величину момента M_A = 6qa 2.

На участке АВ М_х изменяется по линейному закону. Вычисляем момент в сечении В M_B = M_A + = -6qa 2 + qa×a = -5qa 2 и проводим наклонную прямую. Аналогично на участках ВС и СD. В бесконечно близком сечении слева от точки С момент равен M_СB = M_B + = -5qa 2 + 2qa . a = -3qa 2.

В сечении С на эпюре М_х скачок вверх, равный приложенной паре сил M = qa 2 , и правее этого сечения имеем M_CD = M_CB — qa 2 = -3qa 2 — qa 2 = -4qa 2 .

Момент в сечении D M_D = M_CD + = -4qa 2 + 2qa. = -2qa 2 .

На участке DE изгибающий момент изменяется по закону квадратной параболы, обращенной выпуклостью вниз (в сторону погонной нагрузки q). В сечении Е по условию загружения балки М_Е = 0. По двум точкам D и Е приближённо стр

1. Определение опорных реакций. Составляем уравнения равновесия:

, q . 4a . а + qa 2 + 3qa 2 —R_D . 4a = 0,

, R_Ba + qa2 +3qa2-qaa = 0,

П р о в е р к а

, q×4a — R_B — R_D = 4qa — 2qa — 2qa = 0.

2. Построение эпюр поперечной силы и изгибающего момента.

Э п ю р а Q_y. Строится по формуле Q_y = Q_o ± qz. В данном случае перед вторым слагаемым следует взять знак “плюс”, так как погонная нагрузка положительна (см. правила построения эпюр). На участках АВ и ВС эпюра Q_y изображается прямой, наклоненной вверх (в направлении погонной нагрузки q), а на участке CD поперечная сила постоянна (q = 0). В сечениях В и D на балку действуют сосредоточенные силы R_A и R_D, поэтому на эпюре Q_y возникают скачки. Вычисляем значения поперечной силы в характерных точках Q_A = 0,

Э п ю р а М_х. Она строится по формуле Мх = Мо + . На участках с погонной нагрузкой (АВ и ВС) изгибающий момент изменяется по закону квадратной параболы M_x = M_o + Q_oz + 0,5qz 2 , обращенной выпуклостью вверх (в сторону погонной нагрузки q). В сечениях А и D, где приложены сосредоточенные пары, на эпюре М_х наблюдаются скачки, причем момент qa 2 вызывает растяжение сверху (при обходе слева направо), поэтому в сечении А скачок направлен вверх, а момент 3qa 2 вызывает растяжение снизу (при обходе справа налево), поэтому в сечении D скачок происходит вниз. На участке АВ парабола строится по двум точкам А и В, а на участке ВС – по трем точкам (к крайним точкам В и С добавляется точка экстремума). Положение точки экстремума определяется из условия z_o = Q_BC /. Согласно дифференциальной зависимости = dQ/dz = q, поэтому z_o = qa/q = 0. Вычисляем значения момента в характерных точках:

M_A = —qa 2 , M_B = M_A + = -qa 2 + (1/2) . q .a = —qa 2 /2,

M_max = M_B + = —qa 2 /2 — (1/2) .qa . a = —qa 2 ,

M_C = M_max + = —qa 2 + (1/2) . 2 qa . 2a = qa 2

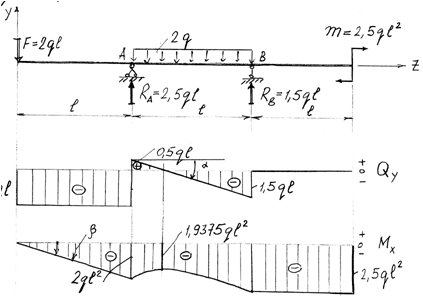
По заданной эпюре поперечной силы Q_y установить нагрузку, действующую на двухопорную балку, и ее опорные реакции. Построить также эпюру изгибающего момента, учитывая, что на правой опоре С приложена пара сил.

Скачки на эпюре Q_y свидетельствуют о приложенных в этих сечениях сосредоточенных силах. Приняв направление обхода слева направо, получим: реакция в точке А равна R_A = qa и направлена вверх; в сечении В приложена сосредоточенная сила F = 5qa, направленная вверх; наконец, реакция R_B = 2qa и направлена вниз. На участке АВ поперечная сила изменяется по линейному закону, что связано с наличием погонной нагрузки, интенсивность которой определяется как тангенс угла наклона прямой q_y = dQ/dz = (-3qa — qa)/4a = —q. Знак “минус” означает, что нагрузка направлена вниз. Для определения неизвестной пары сил М, приложенной в сечении С, составим уравнение моментов относительно этой точки:

, —R_A . 7a — F .3a + q . 4a . 5a + M_C = 0,

откуда M_C = 2qa 2 и направлен против часовой стрелки.

Эпюру М_х строим по формуле М_х = М_о + . На участке АВ изгибающий момент изменяется по квадратичному закону. На концевой шарнирной опоре А нет пары сил, поэтому М_А = 0. В сечении, где Q_y = 0, изгибающий момент принимает экстремальное значение:

M_max = M_A + = (1/2)qa . a = qa 2 /2.

Находим момент в сечении В: M_B = M_max + т = qa 2 /2- (1/2)3qa . 3a = -4qa 2 и по трём точкам приближенно строим параболу, обращенную выпуклостью вниз. На участке ВС изгибающий момент изменяется по линейному закону от M_B = -4qa 2 до M_C = M_B + = -4qa ₂ + 2qa . 3a = 2qa 2 . По условию загружения балки также имеем M_C =2qa 2 . Совпадение значений М_С, найденных независимо друг от друга, свидетельствует о правильности построения эпюры М_х.

По заданной эпюре изгибающего момента построить эпюру поперечной силы и определить нагрузку, действующую на балку. Криволинейный участок эпюры М_х очерчен по квадратной параболе, а кружком отмечена ее вершина.

На участке АВ изгибающий момент изменяется по квадратичному закону: M_x = M_o + Q_oz — 0,5qz 2 . Так как вершина параболы совпадает с точкой А, то М_о = М_А =0 и Q_o = 0. Следовательно, М_х = -0,5qz 2 . Момент в бесконечно близком сечении слева от опоры В, судя по приведенной эпюре, равен М_ВА = -40 кНм. С другой стороны, М_ВА = -0,5q(2) 2 . Следовательно, q = 20 кН/м. Парабола обращена выпуклостью вниз, поэтому и погонная нагрузка направлена вниз.

В сечении В изгибающий момент изменяется скачком от М_ВА = -40 кНм до М_ВС = -10 кНм, что свидетельствует о наличии пары сил М₁ = 30 кНм, вызывающей растяжение нижних волокон (при обходе слева направо), т.е. направленной по часовой стрелке. На опоре С приложена пара сил с моментом М₂ = 20 кНм, вызывающая растяжение снизу (при обходе справа налево), т.е. направленная против часовой стрелки.

На участке ВС поперечная сила постоянна и равна тангенсу угла наклона прямой, т.е. Q_BC = dM/dz = = (20 + 10)/3 = 10 кН. На участке АВ поперечная сила изменяется по линейному закону (Q_y = Q_o — qz) от Q_o = Q_A = 0 до Q_BA = -q = -40 кН. По скачкам на эпюре Q_y находим величины и направления реакций: R_B = 50 кН (направлена вверх) R_C = 10 кН (направлена вниз).

Построить эпюры поперечных сил Q_Y и изгибающего момента M_X (см. рис.1).

1) Проведем две оси, параллельные оси балки (одну для эпюры Q_Y, вторую для эпюры M_X).

2) Балка имеет один участок загружения.

3) Строим эпюру Q_Y. Сделаем сечение (1), отбросим жесткую заделку. Учитывая правило знаков, получим . В сечении (2) получим . Силы , так как сила F поворачивает оставшуюся часть балки вокруг сечения по часовой стрелке (рис.2,а).

Положительные значения поперечной силы откладывают всегда выше оси

Соединим их прямой линией, поставим знак, эпюру заштрихуем, обозначим.

4) Строим эпюру М_Х. Сделав сечение и отбросив часть с жесткой заделкой, сосчитаем момент от силы F относительно сделанного сечения. Получим . Для эпюры изгибающих моментов принимается следующее правило: значения моментов откладываются от оси в сторону растянутого волокна. Из рис.2,б, следует, что сила F растягивает верхние волокна, поэтому полученное значение М_Х откладываем выше оси. Соединяем отложенные значения прямой линией. Знак на эпюре изгибающих моментов можно не ставить. Эпюру штрихуем и обозначаем (рис.1).

5) Проверка эпюр. К балке не приложена распределенная нагрузка, следовательно, на графиках Q_Y и М_Х имеем прямые линии, причем на эпюре Q_Y это прямая, параллельная оси. На свободном конце балки приложена сосредоточенная сила F = 6кН в этом сечении на эпюре Q_Y образовался скачок, равный 6.

Построить эпюры поперечных сил Q_Y и изгибающего момента M_X (см. рис.).

1) Проводим оси для построения эпюр.

2) Делим балку на два участка загружения.

Откладываем значения ниже оси, соединяем прямой линией.

Значение откладываем ниже оси, соединяем прямой линией.

Ставим знаки, эпюру штрихуем и обозначаем.

Откладываем значения ниже оси, так как сила F растягивает нижние волокна, соединяем прямой линией.

Значения откладываем ниже оси и соединяем параболой. При этом выпуклость параболы должна быть обращена в сторону действия распределенной нагрузки. Это правило называют «правилом паруса». Роль паруса здесь играет эпюра, а роль ветра – нагрузка.

5) Проверка эпюр. На участке балки с распределенной нагрузкой получаем на эпюре Q_Y наклонную прямую, на эпюре M_X – параболу. В сечении с приложенной сосредоточенной силой F = 8 кН на эпюре Q_Y образовался скачек равный 8.

Построить эпюры поперечных сил Q_Y и изгибающего момента M_X (см. рис.).

1) Проводим оси для построения эпюр.

2) Делим балку на два участка загружения.

Откладываем значения ниже оси, соединяем прямой линией.

Откладываем ниже оси, а — выше оси, соединяем прямой линией (см. рис.).

Откладываем ниже оси, соединяем с нулем прямой линией.

Из рисунка следует, что эпюра поперечных сил Q_Y на этом участке пересекает ось, то есть в некотором сечении (5) сила . Отсюда следует, что в сечении (5) изгибающий момент М_Х достигает экстремального значения (максимума или минимума). Таким образом, на этом участке следует просчитать момент в трёх точках.

Определим экстремальное значение момента. Выясним сначала, на каком расстоянии Z от правой границы участка находится сечение (5), в котором поперечная сила равна нулю.

Найдем значение момента.

Откладываем значения ниже оси и соединяем параболой по правилу «паруса», то есть выпуклостью вниз (см. рис.).

5) Проверка эпюр. Все линии на эпюрах соответствуют приложенным нагрузкам, силе F = 8 кН соответствует скачок, равный 8 на эпюре Q_Y.

Построить эпюры поперечных сил Q_Y и изгибающего момента M_X (см. рис. 1).

1) Расчёт балки с шарнирным закреплением следует начинать с определения реакций связей. Расставим эти реакции. В шарнирно –подвижной опоре А возникает одна вертикальная реакция R¢_A. В шарнирно-неподвижной опоре В, вообще говоря, возникает две реакции – вертикальная R¢_B и горизонтальная Н_В, однако, поскольку в случае вертикального плоского изгиба все силы действуют перпендикулярно оси балки, горизонтальная реакция Н_В всегда будет равна нулю, поэтому в дальнейшем показывать ее на схеме балки не будем. Вертикальные реакции найдем из уравнений статики.

При записи уравнений использовалось следующее правило знаков: если сила поворачивает балку вокруг т.А (т.В) по часовой стрелке, то момент от этой силы берется со знаком «+».

Для проверки найденных реакций используем уравнение статики: (сумма всех вертикальных сил должна быть равна нулю). При этом силы, изображенные на схеме балки направленными вверх, берем со знаком «+».

Подставим сюда найденные значения реакций со своими знаками.

— 23 + 10 × 2 + 15 – 12 = 0; 35 – 25 =0; 0 = 0.

Поскольку направления вертикальных реакций поначалу были взяты произвольно, то полученные в результате знаки «-» у реакций R_A, R_B показывают, что мы не угадали направление реакций, в действительности они направлены вниз. Удобно изменить направление этих реакций на обратное и в дальнейшем считать эти реакции положительными (см. рис.1).

2) Проводим оси для построения эпюр.

3) Делим балку на три участка загружения.

4) Так как все реакции в закреплениях балки найдены, то, сделав сечение, можно отбрасывать любую (обычно более загруженную) часть балки .

5) Строим эпюру QY.

(отбросили правую часть балки),

(отбросили левую часть балки).

Пару сил М = 20 кНм при вычислении Q_Y, естественно, не учитываем.

Откладываем значения от оси, соединяем прямой линией.

;

;

6) Строим эпюру М_Х.

;

Чтобы не ошибиться в знаке изгибающего момента, сечение, в котором он определяется, следует представлять защемленным, а опоры – отброшенными (рис.2):

Откладываем значения от оси и соединяем параболой по правилу «паруса», то есть направленной выпуклостью вверх.

Откладываем значения выше оси, соединяем прямой линией.

Отложенные от оси значения соединяем прямой линией (рис.1).

6) Проверка эпюр. Все линии на эпюрах соответствуют действующим нагрузкам. К балке приложены три сосредоточенные силы – R_A, F, R_B. На эпюре Q_Y получили три скачка на опоре А – равный R_A = 23, на границе 2-го и 3-го участков – равный F = 3 + 12 = 15, на опоре В – равный R_B = 12. К балке приложена пара сил М = 20. На эпюре М_Х на границе 1-го и 2-го участков имеем скачок, равный М = (26 — 6) = 20.

Построить эпюры поперечных сил Q_Y и изгибающего момента M_X (см. рис.).

1) Найдем реакции опор R_A, R_B.

Обе реакции получились положительными, то есть мы угадали их направление, они действительно направлены вверх.

2) Балка имеет два участка загружения.

3) Строим эпюру Q_Y.

;

Откладываем значения от оси и соединяем прямой линией.

;

Откладываем значения от оси и соединяем прямой (см. рис.).

4) Строим эпюру М_Х.

Из эпюры сил следует, что на этом участке будет возникать экстремальный момент, поэтому будем определять М_Х в трёх сечениях. (отбрасываем правую часть балки); (отбрасываем левую часть балки).

Находим координату Z сечения (5):

Находим экстремальный момент.

Откладываем значения от оси и соединяем параболой по правилу «паруса», то есть выпуклостью вниз.

Отложенные от оси значения соединяем прямой (см. рис.).

5) Проверка эпюр.

Линии эпюры соответствуют приложенным нагрузкам. К балке приложены три сосредоточенные силы – R_A, F, R_B на эпюре Q_Y в соответствующих сечениях имеем скачки.

К балке на опоре В приложена пара сил М: на эпюре М_Х имеем на правом конце скачок, равный М = 48.

Дана балка с действующими на нее нагрузками (рис. а). Требуется определить внутренние усилия – поперечную силу Q и изгибающий момент М в балке, построить графики их изменения вдоль оси стержня (эпюры Q и М).

Прежде всего найдем опорные реакции. Балка имеет жёсткое защемление на правом конце (В балке с заделкой можно строить эпюры Q и М без определения опорных реакций, рассматривая все силы с одной стороны от сечения – со свободного конца. Но студенту, только начинающему осваивать построение эпюр, рекомендуем все же реакции находить. Это дополнительная проверка правильности решения задачи) и в этом закреплении при заданной вертикальной нагрузке возникают две опорные реакции: вертикальная реакция R_A и реактивный момент M_A. Горизонтальная реакция при действии вертикальной нагрузки равна нулю. Это следует из уравнения равновесия «сумма проекций всех сил на горизонтальную ось равна нулю». Определим R_A и M_A, используя два других уравнения статики. Желательно составлять такие уравнения, в каждое из которых входит только одна неизвестная. В данном случае такими уравнениями являются «сумма проекций всех сил на вертикальную ось (ось z) равна нулю» и «сумма моментов всех сил относительно точки А равна нулю»:

;

;

Из первого уравнения найдем R_A = 30 кН, из второго – М_А =5 кНм. Полученные положительные знаки опорных реакций подтверждают выбранные нами направления опорных реакций: R_A – вверх, а М_А – против часовой стрелки. Для проверки рекомендуем использовать любое другое уравнение равновесия, например

– 30×2 – 15×2×1 – 60 + 10×1×2,5 + 30×4+5 = – 150 + 150 = 0.

Теперь определяем внутренние усилия: поперечную силу Q и изгибающий момент М. В соответствии с методом сечений рассекаем балку на каждом участке (в данной задаче их три) произвольным сечением и рассматриваем все силы, расположенные с одной стороны от сечения: слева или справа. Удобно рассматривать все силы с той стороны от сечения, где сил меньше. Начало отсчета координаты x на каждом участке можно выбирать произвольным образом. Например, на рис. а начало отсчета x на каждом участке – свое и находится в начале участка. Запишем выражения для Q и М на каждом участке.

Участок 1: .

Рассмотрим силы, расположенные слева от сечения. По определению поперечной силы и с учетом правила знаков для Q :

Здесь q₁x₁ – равнодействующая равномерно распределенной нагрузки, действующей слева от сечения.

По определению изгибающего момента и с учетом правила знаков для М :

где во втором слагаемом x₁/2– плечо равнодействующей равномерно распределенной нагрузки (q₁x₁), взятой слева от сечения (равнодействующая приложена по середине длины отсеченной части балки x₁).

Для построения эпюр найдем значения Q и М на границах участка:

в конце участка (x₁ =a) ; . ;

Участок 2:

Снова рассмотрим все силы, расположенные слева от сечении

Граничные значения Q и М:

в начале участка (x₂ = 0) ; ,

в конце участка (x₂=b) ; .

Участок 3: .

Теперь рациональнее рассмотреть все силы справа от сечения. Тогда

Из этих выражений следует, что поперечная сила на третьем участке – постоянная величина, а изгибающий момент меняется по линейному закону и на границах участка имеет следующие значения:

в конце участка (x₃=c) .

Запишем результаты определения внутренних усилий в таблицу, сосчитав численные значения Q и М на границах участков (табл. 1).

Из таблицы видно, что поперечная сила на первом участке меняет свой знак, т. е. график Q пересекает нулевую линию. Это значит, что изгибающий момент на этом участке имеет экстремум. Найдем максимальное значение М на этом участке. Сначала определим то значение координаты х₁, при котором поперечная сила равна нулю. Обозначим это значение координаты х₀ (см. рис. ).

х0 = 1,33 м.

Чтобы найти максимальное значение изгибающего момента, подставим х₀ в выражение для М на первом участке:

кНм.

По результатам вычислений в таблице строим эпюры Q и М на каждом участке (см. рис. б). Не забываем после построения эпюр проанализировать результаты по тем правилам проверки правильности построения эпюр, которые перечислены ранее.

На балку кроме равномерно распределенной нагрузки действует линейно распределенная (треугольная) нагрузка (рис. а). Построим эпюры распределения поперечной силы и изгибающего момента, обращая внимание на определение Q и М на участке с треугольной нагрузкой.

Найдём опорные реакции. Балка имеет шарнирное опирание и для определения двух не равных нулю опорных реакций R_A и R_B (горизонтальная реакция H_A = 0) составим два независимых уравнения статики. Рациональными уравнениями, в каждое из которых входит одна неизвестная реакция, в данном случае являются:

;

;

Напомним как определяется момент от треугольной нагрузки. Равнодействующая от треугольной нагрузки равна площади треугольника q₂.b/2 и приложена в центре тяжести треугольника, поэтому плечо этой равнодействующей относительно точки А равно (2/3) .b, а относительно точки В – (b/3)+c. Из этих уравнений найдем R_A = – 31,9 кН, R_B = – 18,1 кН. Отрицательные знаки показывают, что обе реакции направлены не вверх, как показано на рис. а, а в противоположную сторону. Для проверки опорных реакций составим уравнение равновесия «сумма проекций сил на вертикальную ось z равна нулю»:

;

Определение внутренних усилий производим, записывая выражения для Q и М в таблицу (табл. 2).

Поясним выражения для Q и М на втором участке, а именно третьи слагаемые в этих выражениях, учитывающие треугольную нагрузку. Чтобы найти равнодействующую от треугольной нагрузки, расположенной слева от рассматриваемого сечения на участке длиной х₂, определим интенсивность распределенной нагрузки в сечении х₂, которая на рис. а обозначена q_x. Для этого составим пропорцию: , откуда . Тогда равнодействующая этой распределенной нагрузки на участке длиной х₂ . Она приложена в центре тяжести треугольника, и изгибающий момент, создаваемый этой нагрузкой, равен , где – плечо равнодействующей.

Поскольку поперечная сила на втором участке меняет знак, найдем экстремальное значение изгибающего момента в сечении х₀ на этом участке (рис. б). Определим величину х0, приравняв выражение для поперечной силы на втором участке нулю:

, откуда x_{0 = 2,89 м. Тогда}

По полученным в таблице выражениям строим эпюры внутренних усилий. Напомним, что выпуклость эпюры М направлена в сторону распределенной нагрузки. Выпуклость эпюры Q на втором участке можно определить по знаку второй производной . В данном случае функция q(x) является убывающей, следовательно , а . Это означает, что эпюра Q имеет выпуклость вниз. Можно определить выпуклость эпюры поперечной силы и по-другому. В сечении, где интенсивность распределенной нагрузки равна нулю (начало второго участка в данной задаче), угол наклона касательной к кривой Q_(x) должен равняться нулю, так как в этом сечении dQ/dx=0. Это возможно тогда, когда функция Q_(x) имеет выпуклость вниз.

После того, как Вы нарисовали эпюры, рекомендуем обязательно проанализировать их по правилам проверки правильности построения эпюр.

Построить эпюры M_x и Q_y для заданной балки (см. рис.).

1.Предположим, что опорные реакции А и В направлены вверх (рис. а). Из уравнений равновесия имеем:

А_H = 0

B_{v = 40 н;}

A_{v = 60 н;}

Для проверки найденных реакций используем уравнение равновесия.

Уравнение тождественно удовлетворяется, что указывает на правильность определения опорных реакций.

2. Для построения эпюр M_x и Q_y заданную балку разобьем на участки I, II, III таким образом, что бы в пределах каждого участка силовой фактор определялся непрерывной функцией от z. Применим метод сечений к I и III участкам (рис. б). Выражения для внутренних силовых факторов имеют вид:

Построим эпюру Q_y (рис. в), используя выражения Q I _y и Q III _y. Согласно правилам ординаты эпюры Q_y, равны A_v откладываются вверх и постоянны на I и II участках. В сечении D (рис. а), где приложена сила P, на эпюре Q_y будет скачок на величину P и в направлении этой силы. В сечении B, где z₃=0, получаем . По значениям Q_y D , Q_y B поперечной силы в сечениях D и B строим прямую Q_y на III участке. Прямая пересекла ось на расстоянии z₀ от опоры B. Значение z₀ найдем, приравняв нулю. Тогда . В этом сечении на эпюре M_x достигается экстремальное значение.

Согласно правилам эпюра M_x на I участке линейна и положительна. При z₁ = 0 ; при z₁ = 0,15 . Согласно правилу на эпюре M_x в сечении C будет скачек на величину момента m (рис. д). Скачок момента направлен вниз, так как при переходе с I участка на II участок внешний момент m вызывает сжатие нижних волокон (рис. г). На II участке прямая M_{x III} параллельна прямой M_x I , так как производная Q_y на обоих участках одинакова. Значение M_x в сечении D равно . На III участке эпюра M_x согласно правилу имеет вид квадратной параболы, которая выпуклостью направлена навстречу распределенной нагрузке q и имеет максимум в сечении z₃ = z₀.

Найдём . Параболу строим по трём значениям момента M_x D , M_x B =0, M_x III (z₀) . Отметим, что в сечении D на эпюре M_x согласно правилу будет излом.

Проверим выполнение дифференциальных зависимостей на построенных эпюрах Q_y, M_x. На участках I, II производная положительная функция (M_x) возрастает. В сечении D производная (Q_y) имеет скачок, а функция (M_x) имеет излом. В сечении z₃ = z₀ производная (Q_y) равна нулю, функция (M_x) достигает максимума на III участке.

Задачи для самостоятельного решения

Построить эпюры поперечных сил и изгибающих моментов для балок, защемленных одним концом и загруженных, как показано на рисунке. Подсчитать наибольшие по абсолютному значению величины поперечных сил и изгибающих моментов, если F =20 кН, q =20 кН/м, М₀ = 40 кН/м и l =2 м

Построить эпюры поперечных сил и изгибающих моментов для балок на двух опорах, загруженных, как показано на рисунке. Найти mах Q и mах М при следующих данных: F= 60 кН, q =20 кН/м, М₀=60 кНм, l =3 м.

При каком значении силы F изгибающие моменты в опорных сечениях балок, изображенных на рисунке, будут равны нулю? Построить эпюры Q и М при этих значениях сил.

Построить в общем виде эпюры Q_Y и M_X для заданной балки.

Построить эпюры поперечных сил и изгибающих моментов, если L₁=0,2м; L₂=0,3м; q=4 кН/м.

Для изображенного стержня, определить внутренние усилия в сечениях А и В.

Для всех стержней, изображенных ниже, определить вид деформации и построить эпюры соответствующих внутренних усилий. Для самоконтроля приведены уже построенные эпюры.

iSopromat.ru

Внутренние поперечная сила и изгибающий момент возникают в поперечных сечениях балки при её изгибе под действием внешних нагрузок.

Поперечным изгибом называется такой вид деформирования бруса, при котором внешние нагрузки действуют перпендикулярно к его продольной оси. Деформация изгиба заключается в искривлении оси бруса.

Брус с прямой осью, работающий на изгиб, называется балкой. Если плоскость действия внешних нагрузок проходит через ось балки и одну из главных центральных осей поперечного сечения, изгиб называется прямым. В этом случае ось балки искривляется в плоскости действия нагрузок и является плоской кривой.

В сечениях балки возникают два внутренних силовых фактора: изгибающий момент М_х и поперечная сила Q_y

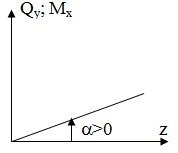
Дифференциальные зависимости между q, Q_y и М_х имеют вид:

1. В сечении, где приложена сосредоточенная сила, — на эпюре Q_y скачок по модулю равный этой силе, на эпюре М_х – излом навстречу силе.
2. В сечении, где приложена сосредоточенная пара сил m — на эпюре М_х скачок по модулю равный этой паре сил. На эпюре Q_y это не сказывается.
3. Если на участке имеется равномерно распределенная нагрузка q, то Q_y изменяется по линейному закону, М_х – по параболе, выпуклостью навстречу нагрузке q (М_х = М_экстр – в сечении, где Q_y меняет свой знак).

Изгиб называется чистым, если в сечении балки возникает только изгибающий момент М_х.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Изгибающий момент | Полный обзор и важные отношения

1. Определение изгибающего момента
2. Уравнение изгибающего момента
3. Связь между интенсивностью нагрузки, поперечной силой и изгибающим моментом
4. Единица измерения изгибающего момента
5. Изгибающий момент балки
6. Соглашение о знаках изгибающего момента
7. Диаграмма усилия сдвига и изгибающего момента
8. Типы опор и нагрузок
9. Вопрос и ответ

Определение изгибающего момента

В механике твердого тела изгибающий момент представляет собой реакцию, возникающую внутри элемента конструкции, когда к нему прикладывается внешняя сила или момент, вызывающие изгиб элемента. Самым передовым, стандартным и простейшим элементом конструкции, подверженным изгибающим моментам, является балка. Если момент, приложенный к балке, пытается изогнуть балку в плоскости стержня, это называется изгибающим моментом. В случае простого изгиба, если изгибающий момент применяется к определенному поперечному сечению, возникающие напряжения называются изгибающим или изгибающим напряжением. Он изменяется линейно от нейтральной оси по поперечному сечению балки.

Уравнение изгибающего момента

Алгебраическая сумма моментов по конкретному поперечному сечению балки, возникающих из-за моментов по часовой или против часовой стрелки, называется изгибающим моментом в этой точке.

Пусть W — вектор силы, действующий в точке A тела. Момент этой силы относительно реперной точки (O) определяется как

Где M = Момент вектор, р = вектор положения от опорной точки (О) до точки приложения силы А. символ обозначает векторное произведение. легко вычислить момент силы вокруг оси, которая проходит через опорную точку O. Если единичный вектор вдоль оси равен «i», момент силы вокруг оси определяется как

где [.]представляют собой точечное произведение вектора.

Математическая связь между интенсивностью нагрузки, поперечной силой и изгибающим моментом

Соотношения: Пусть f = интенсивность нагрузки

Q = поперечная сила

M = изгибающий момент

Скорость изменения поперечной силы даст интенсивность распределенной нагрузки.

Скорость изменения изгибающего момента даст силу сдвига только в этой точке.

Единица измерения изгибающего момента

Изгибающий момент имеет единицу, аналогичную паре как Нм.

Изгибающий момент балки

Предполагая, что балка AB определенной длины подвержена изгибающему моменту M, Если верхнее волокно балки, то есть выше нейтральной оси, находится в состоянии сжатия, это называется положительным изгибающим моментом или прогибающим изгибающим моментом. Точно так же, если верхнее волокно балки, то есть выше нейтральной оси, находится в напряжении, это называется отрицательным изгибающим моментом или изгибающим моментом изгиба.

Соглашение о знаках изгибающего момента

При определении максимального изгибающего момента, вытяжки и BMD соблюдается соглашение о конкретных знаках.

1. Если мы начнем вычислять изгибающий момент с правая сторона или правый конец луч, Момент по часовой стрелке принимается как отрицательныйи Противодействующий момент принимается как Положительно.
2. Если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке принимается как Положительный, и Момент против часовой стрелки принимается как Negative.
3. Если мы начнем вычислять поперечную силу с правая сторона или правый конец луч, Сила, действующая вверх принимается как Отрицательныйи Сила, действующая вниз принимается как Положительно.
4. Если мы начнем вычислять поперечную силу с Левая сторона или левый конец балки, Сила, действующая вверх принимается как Положительный, и Сила, действующая вниз принимается как Negative.

Диаграмма усилия сдвига и изгибающего момента

Сдвигающая сила представляет собой алгебраическую сумму сил, параллельных поперечному сечению по конкретному поперечному сечению балки, возникающих из-за сил действия и противодействия. Сила сдвига пытается срезать поперечное сечение балки перпендикулярно оси балки, и из-за этого развитое распределение напряжения сдвига является параболическим по отношению к нейтральной оси балки. Изгибающий момент представляет собой сумму моментов в определенном поперечном сечении балки, обусловленных моментами по часовой стрелке и против часовой стрелки. Это пытается изогнуть балку в плоскости элемента, и из-за передачи его по поперечному сечению балки распределение развиваемого изгибающего напряжения является линейным относительно нейтральной оси балки.

Диаграмма усилия сдвига — это графическое изображение изменения поперечной силы в поперечном сечении по длине балки. С помощью диаграммы силы сдвига мы можем определить критические секции, подверженные сдвигу, и внести поправки в конструкцию, чтобы избежать разрушения.

Кроме того, Диаграмма изгибающего момента — графическое представление изменения изгибающего момента в поперечном сечении по длине балки. С помощью диаграммы B. M мы можем определить критические секции, подлежащие изгибу, и внести изменения в конструкцию, чтобы избежать отказа. При построении диаграммы поперечных сил [SFD], при построении диаграммы изгибающих моментов [BMD] происходит резкое повышение или резкое падение из-за точечной нагрузки, действующей на балку; происходит внезапный подъем или резкое падение из-за воздействия пар на балку.

Типы опор и нагрузок

Фиксированная поддержка: Он может предложить три реакции в плоскости элемента (1 горизонтальная реакция, 1 вертикальная реакция, 1 моментная реакция).

Поддержка контактов: Он может предложить две реакции в плоскости элемента (1 горизонтальная реакция, 1 вертикальная реакция).

Роликовая опора: Он может предложить только одну реакцию в плоскости члена (1 вертикальная реакция).

Концентрированная или точечная нагрузка: При этом вся интенсивность нагрузки ограничена конечной площадью или точкой.

Равномерно распределенная нагрузка [UDL]: При этом вся интенсивность нагрузки постоянна по длине балки.

Равномерно изменяющаяся нагрузка [UVL]: При этом вся интенсивность нагрузки изменяется линейно по длине балки.

Диаграмма усилия сдвига и диаграмма изгибающего момента только для балки, несущей точечную нагрузку.

Учитывайте только опорную балку, показанную на рисунке ниже, несущую только точечные нагрузки. В балке с простой опорой один конец опирается на штифт, а другой конец — на роликовую опору.

Значение реакции в точках A и B можно рассчитать, применяя условия равновесия

Для вертикального равновесия

Принимая момент относительно A, положительный момент по часовой стрелке и отрицательный момент против часовой стрелки.

Ставя ценность R_B в [1] получаем

Пусть XX — интересующий участок на расстоянии x от конца A.

В соответствии с обсуждавшимся ранее соглашением о знаках, если мы начнем вычислять поперечную силу с Левая сторона или левый конец балки, Сила, действующая вверх принимается как Положительный, и Сила, действующая вниз принимается как Negative.

Сила сдвига в точке А

Мы знаем, что поперечная сила остается постоянной между точками приложения точечных нагрузок.

Сила сдвига при C

Сдвигающая сила в области XX равна

Сила сдвига в точке B

Для диаграммы изгибающего момента, если мы начнем расчет BM с Левая сторона или левый конец балки, Момент по часовой стрелке воспринимается как положительный. Момент против часовой стрелки принимается как Negative.

• при A = 0
• при B = 0
• в C

Сдвигающая сила [SFD] и диаграмма изгибающего момента [BMD] только для консольной балки с равномерно распределенной нагрузкой (UDL).

Рассмотрим только консольную балку, показанную на рисунке ниже UDL. В консольной балке один конец зафиксирован, а другой конец может двигаться.

Результирующая нагрузка, действующая на балку из-за UDL, может быть определена как

W = Площадь прямоугольника

Эквивалентная точечная нагрузка wL будет действовать в центре луча. т.е. при L / 2

Диаграмма свободного тела луча становится

Значение реакции в точке А можно рассчитать, применив условия равновесия.

Для горизонтального равновесия

Для вертикального равновесия

Принимая момент относительно A, положительный момент по часовой стрелке и отрицательный момент против часовой стрелки.

Пусть XX — интересующий участок на расстоянии x от свободного конца.

В соответствии с обсуждавшимся ранее соглашением о знаках, если мы начнем вычислять поперечную силу с Левая сторона или левый конец балки, Сила, действующая вверх принимается как Положительный, и Сила, действующая вниз принимается как Negative.

Сила сдвига в точке A составляет

Сила сдвига в точке B составляет

Значения силы сдвига в точках A и B показывают, что сила сдвига изменяется линейно от фиксированного конца к свободному концу.

Для BMD, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке принимается как Положительный и Момент против часовой стрелки принимается как Negative.

Диаграмма SFD и BMD для консольной балки с равномерно распределенной нагрузкой

4-точечная диаграмма изгибающего момента и уравнения

Рассмотрим балку с простой опорой, у которой две равные нагрузки W действуют на расстоянии a от обоих концов.

Значение реакции в точках A и B можно рассчитать, применив условия равновесия.

Для вертикального равновесия

Принимая момент относительно A, положительный момент по часовой стрелке и отрицательный момент против часовой стрелки.

Согласно описанному ранее соглашению о знаках, если мы начинаем вычислять поперечную силу с левой стороны или с левого конца балки, сила, действующая вверх, принимается как положительная, а сила, действующая вниз, принимается как отрицательная. Для построения диаграммы BMD, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке принимается как Положительный и Момент против часовой стрелки принимается как Negative.

Сила сдвига в точке A составляет

Сила сдвига в C составляет

Сила сдвига в D составляет

Сила сдвига в точке B составляет

Для диаграммы изгибающего момента

Вопрос и ответ изгибающего момента

В.1) В чем разница между моментом и изгибающим моментом?

Ответ: Момент можно определить как произведение силы и длины линии, проходящей через точку опоры и перпендикулярной силе. Изгибающий момент — это реакция, возникающая внутри элемента конструкции, когда к нему прикладывается внешняя сила или момент, вызывающие изгиб элемента.

Q.2) Что такое определение диаграммы изгибающего момента?

Ответ: Диаграмма изгибающего момента — Графическое изображение изменения BM по поперечному сечению по длине балки. С помощью этой схемы мы можем определить критические участки, подлежащие изгибу, и внести изменения в конструкцию, чтобы избежать сбоев.

В.3) Какова формула напряжения изгиба?

Ответ: изгиб Напряжение можно определить как сопротивление, вызванное изгибающим моментом или двумя равными и противоположными парами в плоскости элемента. Его формула дается

Где M = приложенный изгибающий момент по поперечному сечению балки.

I = Второй момент инерции площади

σ = изгибное напряжение, вызванное в стержне

y = расстояние по вертикали между нейтральной осью луча и желаемым волокном или элементом в мм

E = модуль Юнга в МПа

R = радиус кривизны в мм

Знать о прочности материала нажмите сюда

Новые релизы по механической и термической обработке