Уравнение постоянства расхода для потока жидкости

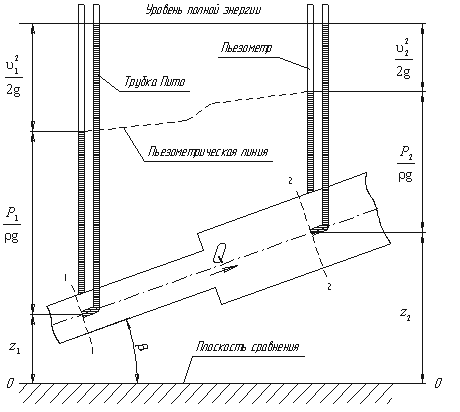
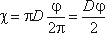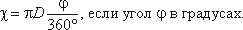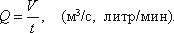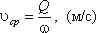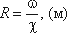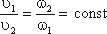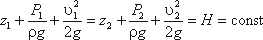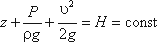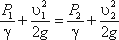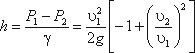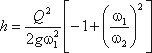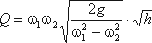Лекция по электроснабжение предприятий

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Тема: Основные уравнения движения

1. Уравнение неразрывности потока. Уравнение постоянства расхода

3. Уравнение Бернулли и его практическое применение

4. Дифференциальные уравнения движения идеальной и вязкой жидкости

5. Основные характеристики турбулентного движения

6. Подобие и моделирование гидромеханических процессов

1. Уравнение неразрывности потока. Уравнение постоянства расхода

Уравнение неразрывности элементарной струйки: скорости и площади поперечных сечений струек в различных живых сечениях могут меняться, однако произведение скорости отдельных частиц струйки на площади их поперечного сечения остаются постоянными

. (4.1)

Рассмотрим установившееся движение в русле переменного сечения (рисунок 4.1). Выберем два произвольных сечения I — I и II — II , нормальных к оси потока, и рассмотрим участок потока, заключённый между сечениями.

Рисунок 4.1 – Схема к уравнениям постоянства расхода и неразрывности потока

Так как жидкость несжимаема, а стенки русла жёсткие, то на основе второго свойства элементарной струйки можно записать уравнение постоянства расхода

. (4.2)

Уравнение постоянства расхода гласит: в любом сечении потока при установившемся движении несжимаемой жидкости её расход одинаков.

Так как , то получаем уравнение неразрывности потока

. (4.3)

Уравнение неразрывности потока гласит: при установившемся движении несжимаемой жидкости произведение средней скорости потока на площадь живого сечения является постоянной величиной.

Через сечения потока жидкости в единицу времени проходит одно и то же количество жидкости

. (4.4)

Из уравнения 4.4 следует, что средние скорости потока обратно пропорциональны площадям соответствующих сечений

или . (4.5)

Дифференциальное уравнение неразрывности имеет вид

, (4.6)

где — расход элементарной струйки;

— бесконечно малая площадь поперечного сечения струйки;

— скорость в поперечном сечении элементарной струйки.

Энергия – это физическая величина, которая показывает, какую работу, может совершить тело.

Известно, что механическая энергия любого тела характеризуется двумя величинами:

а) кинетической энергией (это энергия движения, зависящая от массы тела и скорости его движения)

, (4.7)

где — масса тела или частицы;

— скорость движения тела или частицы;

б) потенциальной энергией (это энергия, которая определяется взаимным расположением тел или частей одного тела).

Потенциальная энергия тела или частицы, поднятого на высоту

. (4.8)

Если масса жидкого тела занимает объём и находится под давлением , то это тело ещё обладает потенциальной энергией давления

. (4.9)

Полная механическая энергия элементарной струйки (частицы) определяется по формуле

, (4.10)

где — масса элементарной струйки (частицы);

— скорость элементарной струйки (частицы).

Удельная энергия струйки – это энергия, отнесённая к единице веса.

, (4.11)

где — удельная кинетическая энергия струйки;

— удельная потенциальная энергия струйки.

Так как поток жидкости представляет собой совокупность множества элементарных струек, и, принимая движение потока установившимся или плавно изменяющимся, можно определить удельную энергию потока жидкости конечных размеров.

Рассмотрим поток жидкости в виде наклонной трубы с плавно изменяющимся сечением (рисунок 4.2).

Рисунок 4.2 – Схема к выводу уравнения энергии потока жидкости

Внутри потока выделим некоторую точку . Обозначим расстояние от этой точки до произвольно выбранной плоскости (плоскость сравнения) — , давление жидкости в центре тяжести сечения — , среднюю скорость движения жидкости в выбранном сечении — .

Полная энергия потока будет равна

,

где — удельная кинетическая энергия потока;

— удельная потенциальная энергия.

Удельная кинетическая энергия определяется

, (4.12)

где — число элементарных струек;

— скорости элементарных струек;

— средняя скорость потока;

— коэффициент, учитывающий неравномерность распределения скорости по сечению.

Удельная потенциальная энергия согласно гидростатическому закону определяется

, (4.13)

то есть для всех точек данного объёма покоящейся жидкости удельная потенциальная энергия относительно выбранной плоскости сравнения постоянна.

Тогда полная удельная энергия потока в выбранном сечении примет вид

. (4.14)

Так как распределение скоростей в потоке неизвестно, то в механике жидкостей и газов эти скорости принимаются одинаковыми, а при определении кинетической энергии потока вводится поправочный коэффициент .

Поправочный коэффициент — коэффициент кинетической энергии (коэффициент Кориолиса) учитывает изменение кинетической энергии из-за неравномерного распределения скоростей в живом сечении потока.

— для равномерных турбулентных потоков.

— для равномерных ламинарных потоков.

3. Уравнение Бернулли и его практическое применение

В потоке жидкости, движущейся в трубке с плавно изменяющимся сечением (рисунок 4.3), выберем два произвольных сечения I — I и II — II . Обозначим и — давления в центрах тяжести сечений и , и — средние скорости, и — вертикальные координаты оси потока в выбранных сечениях.

Рисунок 4.3 – Схема к выводу уравнения Бернулли

Тогда величины полной удельной энергии потока в сечениях I и II соответственно могут быть записаны

. (4.15)

. (4.16)

При движении реальной жидкости часть энергии затрачивается на преодоление силы трения (сопротивления) на пути от первого сечения до второго. Эта энергия обращается в тепло и рассеивается.

Величину потерь обозначим .

Тогда баланс энергии в сечениях I и II (уравнение Бернулли для реального потока жидкости) можно записать

, (4.17)

, (4.18)

где — высота скоростного потока;

— пьезометрическая высота, отсчитываемая в каждом сечении по пьезометру;

— геометрическая высота;

— потерянный напор, равный части энергии, превращённой в тепло.

Уравнение Бернулли устанавливает математическую связь между основными элементами движения жидкости, то есть средней скоростью и гидродинамическим давлением. Оно показывает, что за счёт преобразования одного вида энергии в другой наблюдается при возрастании скорости и уменьшение давления и, наоборот, при уменьшении скорости – возрастание давления.

Физический (энергетический) смысл уравнения Бернулли состоит в том, что при установившемся движении жидкости сумма трёх удельных энергий (положения, давления и кинетической) остаётся неизменной.

Гидродинамический напор – это сумма скоростного напора, геометрической и пьезометрической высот

. (4.19)

На основании уравнения Бернулли сконструирован ряд приборов (водомер Вентури, водоструйный насос, эжектор и др.).

Рассмотрим применение уравнения Бернулли на примере водомерного устройства в трубах – водомера Вентури (рисунок 4.4), который представляет собой вставку в основную трубу диаметром трубы меньшего диаметра . Труба меньшего диаметра соединена с основной трубой коническими переходами.

В основной трубе (сечение I — I ) и в суженном сечении (сечение II — II ) присоединены пьезометры, по показаниям которых определяется расход жидкости в трубе.

Рисунок 4.4 – Схема водомера Вентури

Выведем общую формулу водомера для определения расхода жидкости.

Примем для заданных условий ; и ( из-за малости расстояния между сечениями). Составим уравнение Бернулли для точек, расположенных в центре тяжести сечений при плоскости сравнения О-О, проходящей по оси трубы

или .

Из рисунка 4.4 видно, что

→ .

В последнем уравнении неизвестны величины и . Применяя уравнение неразрывности, можно записать , откуда .

.

Скорость течения в основной трубе (сечение I — I ) равна

.

Так как , то .

Обозначим постоянную величину для данного водомера через :

, тогда ,

где — коэффициент, учитывающий потери напора в водомере, принимается равным 0,96…0,98.

Таким образом, зная диаметры водомера в расширенном и суженном сечениях, по разности давлений , измеряемой пьезометрами, можно легко определить расход воды.

В водоструйном насосе (рисунок 4.5) вода из бака 1 поступает в трубу, имеющую сужение. В узком сечении трубы скорость возрастает. При этом в соответствии с уравнением Бернулли давление здесь падает ниже атмосферного, поэтому происходит подсасывание жидкости по трубке, опущенной в бак 2. При больших скоростях движения жидкость будет подсасываться из бака 2 непрерывно.

Рисунок 7.5 – Схема водоструйного насоса

Скорость течения движущейся жидкости можно определить трубкой Пито . Этот прибор (рисунок 4.6) представляет собой стеклянную трубку, открытую с двух концов. При этом изогнутый под прямым углом конец трубки располагается в жидкости так, чтобы ось нижнего колена совпадала с линией тока.

Рисунок 4.6 – Схема прибора с трубкой Пито

В трубке Пито создаётся дополнительное давление от воздействия скорости движущейся жидкости (скоростной напор)

; ;

практически ,

где — коэффициент, зависящий от конструкции трубки и определяемый путём тарировки.

4. Дифференциальные уравнения движения идеальной и вязкой жидкости

Рассматриваемые уравнения представляют собой математическое выражение закона сохранения количества движения применительно к жидкому элементу: скорость изменения вектора количества движения равна сумме всех массовых и поверхностных сил, действующих на рассматриваемый жидкий элемент.

В качестве такого элемента используем жидкий прямоугольный параллелепипед с рёбрами (рисунок 4.7), на который действуют суммарный вектор поверхностных сил и вектор массовых сил, причём оба эти вектора отнесены к единице объёма.

Рисунок 4.7 – Схема к выводу дифференциальных уравнений движения идеальной жидкости

В данном случае рассматривается движение идеальной жидкости. Единственной поверхностной силой является сила, обусловленная гидродинамическим давлением .

На грани, перпендикулярные оси , будут действовать следующие силы: на левую грань — ; на правую грань — .

Учитывая принятое направление осей, получаем для поверхностей силы, отнесённой к единице объёма, действующей в направлении оси , .

Аналогично ; .

Уравнения движения идеальной жидкости (уравнения Эйлера) имеют вид

;

; (4.20)

.

Для плоского установившегося движения уравнения Эйлера имеют вид

;

. (4.21)

При одномерном течении (когда параметры потока и скорость зависят только от одной координаты) уравнение Эйлера имеет вид

. (4.22)

Уравнения движения, записанные с учётом сил вязкости, существенно усложняются. В отличие от идеальной жидкости поверхностные силы в общем случае направлены не нормально, а под произвольным углом к выделенной площадке.

Для вязкой жидкости уравнение движения (уравнение Навье-Стокса) имеет вид

;

; (4.23)

;

.

5. Основные характеристики турбулентного движения

Для турбулентного режима характерны перемешивание жидкости , пульсации скоростей и давлений в процессе движения. Поэтому механизм турбулентного потока очень сложен.

Движение жидкости становится турбулентным при достижении числом Рейнольдса критического значения. Тогда от стенок трубы отрываются отдельные жидкие массы, попадающие внутрь потока и своим перемещением нарушающие существовавшее до того упорядоченное (подслойное) движение.

В результате возникает диффузия образовавшихся у стенки вихрей, сопровождающаяся гашением заключённой в вихрях кинетической энергии турбулентности. При этом механическая энергия потока переходит частично в тепловую.

Из-за интенсивного вихреобразования частицы жидкости при турбулентном движении описывают весьма сложные траектории, а местные скорости не сохраняются постоянными даже в том случае, когда расход потока постоянен во времени.

Установившегося движения в турбулентном потоке не существует. В каждой точке потока скорость непрерывно меняется по величине и направлению.

Мгновенная местная скорость – это скорость в точке турбулентного потока.

Разложим мгновенную скорость на три взаимно перпендикулярных направления. Получим продольную составляющую , направленную по нормали к живому сечению, и две поперечные составляющие и , лежащие в плоскости живого сечения потока (рисунок 4.8).

Рисунок 4.8 – Составляющие пульсационных скоростей в турбулентном потоке

Как продольные, так и поперечные составляющие мгновенной скорости всё время меняются.

Пульсация скорости – это изменение во времени проекции мгновенной местной скорости на какое-либо направление. Пульсация скорости наблюдается с помощью чувствительных приборов. На рисунке 4.9 показан график пульсации.

Рисунок 4.9 – Пульсация мгновенной местной скорости в турбулентном потоке

Изменения скорости кажутся беспорядочными, но осреднённое за достаточно длинный промежуток времени значение скорости сохраняется постоянным. Это значит, что скорость непрерывно пульсирует около некоторого среднего (осреднённого во времени) значения .

Пульсировать – это подвергаться знакопеременным изменениям относительно какой-то средней величины.

Графически осреднённая скорость выражается высотой прямоугольника, равновеликого площади, заключённой между пульсационной кривой, осью абсцисс и двумя ординатами, соответствующими начальному и конечному моменту наблюдения. Для определения осреднённой скорости важно иметь достаточный период наблюдений, так как закономерной периодичности пульсационных кривых не обнаружено.

Осреднённая скорость – средняя скорость движения в данной точке, определяемая за достаточно продолжительный промежуток времени.

Пульсационная составляющая скорости (пульсационная добавка) – это разность между истинным и осреднённым значением местной скорости. Пульсационные добавки обозначаются теми же буквами, что и сами скорости, но со штрихом.

Пульсационная составляющая в продольном направлении имеет вид

. (4.24)

В турбулентном потоке вместо поля мгновенных скоростей можно рассматривать поле осреднённых скоростей. Только имея в виду осреднённые скорости, можно говорить об установившемся турбулентном движении.

Уравнение осреднённого движения турбулентного потока (уравнение Рейнольдса) имеет вид

, (4.25)

где — период наблюдений.

Также можно осреднить и другие компоненты скорости — и , а также любую другую быстро меняющуюся во времени величину, например произведение скоростей и , давление и другие.

Обычно рассматриваются не истинная, а только осреднённая скорость, а также поле осреднённых скоростей.

Вопросы для самопроверки

1 Как выглядит уравнение неразрывности элементарной струйки?

2 Какой вид имеет уравнение неразрывности потока и о чём оно гласит?

3 Что такое энергия?

4 Какими величинами характеризуется механическая энергия любого тела?

5 В чём заключается различие между кинетической и потенциальной энергиями?

6 Как определяется полная механическая энергия элементарной струйки?

7 Как определить удельную энергию струйки?

8 Чему равна полная энергия потока?

9 Как определить удельную кинетическую и удельную потенциальную энергии?

10 Чему равна полная удельная энергия потока?

11 Что учитывает коэффициент Кориолиса?

12 Какой вид имеет уравнение Бернулли для реального потока жидкости?

13 В чём заключается энергетический смысл уравнения Бернулли?

14 Что такое гидродинамический напор?

15 Как применяется уравнение Бернулли для водомера Вентури?

16 Практическое применение уравнения Бернулли на примере водоструйного насоса.

17 Что представляет собой трубка Пито?

18 Какой вид имеет дифференциальное уравнение движения идеальной жидкости?

19 как запишется уравнение Эйлера для плоского установившегося движения и одномерного течения?

20 какой вид имеет дифференциальное уравнение движения для вязкой жидкости?

21 Каковы основные характеристики турбулентного движения?

22 Дайте определение понятию мгновенной местной скорости.

23 Что такое пульсация скорости?

24 Что называется осреднённой скоростью и пульсационной составляющей скорости?

Уравнение постоянства расхода

Уравнение постоянства расхода

Основные теоретические сведения

Объёмным расходом потока Q называется объём жидкости V, проходящий в единицу времени t через живое сечение потока, м 3 /с:

Q = 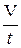. (6.1)

Массовым расходом потока Q_m называется масса жидкости m, проходящий в единицу времени t через живое сечение потока, кг/с:

Q_m = . (6.2)

Уравнение неразрывности течения (сплошности потока) в интегральной форме в случае одномерного приближения принимает вид уравнения постоянства расхода:

· для слобосжимаемой (или трудносжимаемой) жидкости (r = const) это уравнение постоянства объёмного расхода – объёмный расход потока вдоль по течению неизменен.

где Q – объёмный расход, м 3 /с;

v – средняя скорость в живом (поперечном) сечении потока, м/с;

w – площадь живого (поперечного) сечения потока, м 2 .

· для сжимаемой жидкости (r ¹ const) это уравнение постоянства массового расхода – массовый расход потока вдоль по течению неизменен.

где Q_m – массовый расход, кг/с

r – плотность жидкости, кг/м 3 .

Примеры решения задач

Пример № 6.1. Определите массу жидкости плотностью 780 кг/м 3 , которая пройдёт через живое сечение круглого напорного трубопровода диаметром d = 0,2 м за 10 минут. Средняя скорость жидкости в поперечном сечении потока v равна 1,5 м/с.

Массу жидкости, проходящую через живое сечение трубопровода за время t можно определить из уравнения (6.2) Q_m = :

В системе СИ время t = 10 × 60 = 600 с.

Массовый расход жидкости определяем, используя уравнение постоянства массового расхода (6.4). Учитываем, что для круглого напорного трубопровода площадь живого сечения w = .

Q_m = r × v × w = r × v × ;

Q_m = 780 × 1,5× = 36,738 (кг/с).

Искомая масса жидкости равна:

m = 36,738 × 600 = 22042,8 (кг).

Пример № 6.2. Определите размер квадратного напорного трубопровода. За 3 минуты через поперечное сечение трубопровода проходит 7,2 м 3 жидкости постоянной плотности. Средняя скорость потока в живом сечении составляет 1,0 м/с.

Размер, то есть сторону квадратного напорного трубопровода при r = const можно определить из уравнения постоянства объёмного расхода (6.3) Q = v × w:

w = .

Для квадратного напорного трубопровода площадь живого (поперечного) сечения потока w = a 2 . Тогда размер трубопровода равен:

а = .

По уравнению (6.1) объёмный расход потока Q равен:

Q = .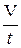

В системе СИ время t = 3 × 60 = 180 с.

Q = = 0,04 (м 3 /с).

w = = 0,04 (м 2 ).

а = = 0,2 (м).

Уравнение Бернулли для потока идеальной жидкости (без учёта потерь энергии)

Примеры решения задач

Пример № 7.1. Определить расход жидкости Q в горизонтальном трубопроводе диаметром d₁ = 0,2 м, имеющем сужение диаметром d₂ = 0,12 м (рис. 7.1). Разность показаний пьезометров Dh = 250 мм.

Dh = 250 мм = 0,25 м.

Рисунок 7.1 Определить: Q.

Составим уравнение Бернулли (энергии) без учёта потерь энергии для двух сечений: 1-1 и 2-2:

z₁ + + a₁ × = z₂ + + a₂ × .

Для горизонтального трубопровода z₁ = z₂. Обозначим пьезометрические высоты h₁ = , а h₂ = . Разность показаний пьезометров равна Dh = h₁ — h₂. Уравнение Бернулли принимает вид:

Dh = a₂ × — a₁ × .

Из уравнения неразрывности v₁ × w₁ = v₂ × w₂ выразим скорость во втором сечении:

v₂ = v₁ × .

Для круглого напорного трубопровода площадь живого сечения потока w = . Тогда

v₂ = v₁ × .

Подставляя это выражение в уравнение Бернулли имеем:

Dh = a₂ × — a₁ × .

Считаем, что течение жидкости в трубопроводе турбулентное. Принимаем коэффициент Кориолиса a₁ = a₂ = a = 1,1.

Dh = a × .

v₁ = = = 0,815 (м/с).

Объёмный расход равен:

Q = v₁ × w₁ = v₁ × = 0,815 = 0,0256 (м 3 /с).

Пример № 7.2. Жидкость вытекает из резервуара большого сечения по горизонтальному трубопроводу переменного сечения. Определить расход Q в горизонтальном трубопроводе (рис. 7.2), скорость на каждом из участков v_i и построить пьезометрическую линию . Напор над центром отверстия, к которому присоединён трубопровод, Н равен 5 м. Диаметры различных участков трубопровода соответственно равны: d₁ = 15 мм, d₂ = 20 мм, d₃ = 10 мм.

Рисунок 7.2 Решение

Составим уравнение Бернулли (энергии) без учёта потерь энергии для двух сечений: 0-0 (свободная поверхность жидкость в резервуаре, из которого истекает жидкость) и 3-3 (выходное сечение трубопровода):

z₀ + + a₀ × = z₃ + + a₃ × .

Здесь р₀ – давление на свободную поверхность жидкости в открытом резервуаре равно атмосферному давлению, то есть р₀ = р_бар. р₃ – давление в выходном сечении трубопровода. Оно равно давлению той среды, куда происходит истечение. В данном случае р₃ = р_бар.

Горизонтальную плоскость сравнения совместим с осью трубопровода переменного сечения. Тогда z₀ = Н, а z₃ = 0.

Скорость на свободной поверхности жидкости в резервуаре v₀ пренебрежимо мала по сравнению со скоростью жидкости в трубопроводе переменного сечения v_i. Поэтому полагаем, что v₀ » 0.

Принимаем, что коэффициент Кориолиса a.₃ =1,0. (На практике мы обычно имеем дело с турбулентным движением жидкости.). Уравнение Бернулли имеет вид:

Н + + 0 = 0 + + 1 ×

Н = .

v₃ = = = 9,9 (м/с).

Используя уравнение неразрывности течения определяем расход жидкости в трубопроводе:

Q = v₃ × w₃ = v × 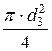= 9,9 × = 0,00078 (м 3 /с).

Используя это же уравнение, определяем скорости на участках диаметром d₁ и d₂:

Q = v₁ × w₁. Þ v₁ = = = = 4,42 (м/с);

Q = v₂ × w₂. Þ v₂ = = = = 2,48 (м/с).

Пьезометрическую линию строят, исходя из следующих положений. Поскольку задача решается без учёта потерь энергии, то напорная линия (линия полной энергии) — будет представлять собой горизонтальную прямую, являющуюся продолжением свободной поверхности воды в сечении 0-0. Пьезометрическая линия расположиться ниже напорной линии на величину в каждом сечении. Таким образом, отложив вниз от напорной линии величины в сечениях, соответствующих изменению диаметра трубопровода, получим ряд точек, соединив которые построим пьезометрическую линию. При этом

= = 0,987 (м);

= = 0,312 (м);

= = 5 (м).

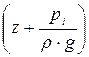
Рисунок 7.3 – Построение пьезометрической линии

Примеры решения задач

Пример № 8.1. При каком режиме будет протекать вода с температурой = 15 °С в открытом прямоугольном лотке, если объёмный расход жидкости Q равен 0,56 м 3 /с, глубина воды в лотке b = 0,7 м, а ширина лотка b = 0,8 м.

Дано = 15 °С;

При температуре = 15 °С коэффициент кинематической вязкости воды n = 1,15 × 10 — 6 м 2 /с [прил. ?].

Для определения режима течения необходимо сравнить расчётное число Рейнольдса Re с критическим значением. Принимаем, что критическое значение числа Рейнольдса равно Re_кр = 2320.

Расчётное число Рейнольдса определяем по формуле:

Re_{d экв} = ,

где v -средняя скорость течения воды в открытом лотке;

— диаметр эквивалентный, м;

n — кинематический коэффициент вязкости м 2 /с.

Среднюю скорость течения воды в открытом лотке определяем из уравнения неразрывности течения

где w – площадь живого (поперечного) сечения потока, м 2 . Для прямоугольного лотка площадь живого сечения равна

v = = = = 1,0 м/с.

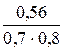
Диаметр эквивалентный d_экв – это отношение четырёх площадей живого сечения потока w к смоченному периметру c:

d_экв =

Смоченный периметр c (хи) – часть периметра живого сечения, на которой жидкость соприкасается с твёрдыми стенками. Для открытого прямоугольного лотка смоченный периметр равен c = h + h + h = 2 × h + b.

d_экв = = = = = 1,02 м.

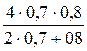
Re_{d экв} = = 886956,52.

Re > Re_кр, следовательно режим движения турбулентный.

Пример № 8.2. По напорному трубопроводу переменного сечения подаётся жидкость с объёмным расходом Q = 0,6 л/с. Кинематический коэффициент вязкости жидкости 3,2×10 — 6 м 2 /с. Определите диаметр, при котором произойдёт смена режима движения.

Дано Q = 0,6 л/с = 0,6×10 — 3 м 3 /с;

n = 3,2×10 — 6 м 2 /с.

Смена режима движения происходит при Re_кр = для цилиндрических напорных труб:

Re_кр = = 2000…2320,

где v -средняя скорость в поперечном сечении потока;

d — диаметр трубопровода, м;

n — кинематический коэффициент вязкости м 2 /с.

Среднюю скорость течения жидкости выразим из уравнения неразрывности течения Q = v × w:

v = ,

где w – площадь живого (поперечного) сечения потока, м 2 .

Для круглого напорного трубопровода площадь живого сечения потока равна:

w = .

v = = .

Подставляем это выражение в формулу для определения числа Рейнольдса:

Re_кр = = = .

Отсюда диаметр, при котором происходит смена режима течения, равен:

d = .

Принимаем, что критическое значение числа Рейнольдса равно Re_кр = 2320. Тогда

d = = 0,1 (м).

Примеры решения задач

Пример № 10.1. Определить потери давления на трение Dр_тр в стальной трубе квадратного сечения. Длина трубы l = 80 м, площадь живого сечения w = 2,25×10 — 2 м 2 , средняя скорость движения воды v = 5 м/с, температура воды 20 0 С.

— плотность воды r = 998,2 кг/м 3 ;

— абсолютная эквивалентная шероховатость k_э = 0,05 мм;

— кинематический коэффициент вязкости n = 1,01´10 — 6 м 2 /с.

Потери давления на трение определяем по формуле Дарси-Вейсбаха:

Dр_тр = l × × r × ,

где d_экв – эквивалентный диаметр рассматриваемого участка трубы, м;

— коэффициент гидравлического трения (коэффициент Дарси), безразмерный;

— длина трубопровода, м;

— диаметр трубопровода, м;

r — плотность жидкости, кг/м 3 ;

v – средняя скорость течения жидкости в сечении потока, м/с.

Диаметр эквивалентный d_экв равен отношение четырёх площадей живого сечения потока w к смоченному периметру c. Для трубопровода квадратного сечения со стороной а диаметр эквивалентный равен:

d_экв = = = а.

Величину а определяем из площади квадрата (w = а 2 ). а = = = 0,15 м.

Определяем режим течения жидкости в трубопроводе:

Re = = = 742574,26.

Значение числа Рейнольдса больше критического (Re_кр = 2320), следовательно, режим течения жидкости турбулентный.

Определяем значение критерия зоны турбулентности:

Re × = 742574,26 × = 247,86.

Значение критерия зоны сопротивления находится в пределах от 10 до 500, следовательно движение происходит в области смешанного сопротивления, для которой справедлива формула Альтшуля:

l = 0,11 × = 0,11 × = 0,0158.

Потери давления на трение равны:

Dр_тр = 0,0158 × × 998,2 × = 105143,73 Па.

Пример № 10.2. Определить потери напора и гидравлический уклон при подаче воды со скоростью v = 0,2 м/с через умеренно заржавленную стальную трубку диаметром d = 50 мм и длиной l = 60 м при температуре воды 10 0 С.

— кинематический коэффициент вязкости n = 1,31´10 — 6 м 2 /с;

— абсолютная эквивалентная шероховатость k_э = 0,45 мм.

Потери напора на трение определяем по формуле Дарси-Вейсбаха:

Dh_тр = l × × ;

где — коэффициент гидравлического трения (коэффициент Дарси), безразмерный;

— длина трубопровода, м;

— диаметр трубопровода, м;

v – средняя скорость течения жидкости в сечении потока, м/с.

Определяем режим течения жидкости в трубопроводе:

Re = = = 7633,59.

Значение числа Рейнольдса больше критического (Re_кр = 2320), следовательно, режим течения жидкости турбулентный.

Определяем значение критерия зоны турбулентности:

Re × = 7633,59 × = 9,16.

Значение критерия зоны сопротивления меньше 10, следовательно движение происходит в области «гидравлически гладких» труб, для которой справедлива формула Блазиуса:

l = = = 0,0338.

Dh_тр = 0,0338 × × = 0,083 м.

Гидравлическим уклоном i называется отношение потерь напора Dh_тр к длине участка l, на котором эти потери происходят:

i = = = 0,00138 м/м.

Примеры решения задач

Пример № 11.1.

В качестве нагревательных приборов системы отопления использованы стальные трубы d₁ = 0,6 м. Стояк, подводящий нагретую воду, и соединительные линии выполнены из труб диаметром d₂ = 0,025 м и приварены к торцам нагревательных труб (рис. 9.1). Определить суммарные потери давления на участке между сечениями А-А и В-В, если скорость движения горячей воды в подводящих линиях v₂ = 1,0 м/с. Радиус поворота нагревательной трубы R_п = 0,6 м, а длина нагревательной трубы l₁ = 4,0 м. Температура воды = 90 0 С.

Дано: d₁ = 0,6 м;

= 90 0 С.

Справочные данные: r = 965,3 кг/м 3 ;

n = 0,33×10 — 6 м 2 /с;

при плавном повороте трубопровода круглого сечения на 180 0 а = 1,33.

Общие потери давления в системе между сечениями А-А и В-В русел равны арифметической сумме потерь давления по длине l₁ и всех потерь, вызванных отдельными местными сопротивлениями (внезапное расширение, плавный поворот на 180 0 и внезапное сужение).

р_пот = + = Dр_{тр 1} + Dр_{м в.р} +Dр_{м 180} +Dр_{м в.с.}.

Потери давления на трение по длине на участке длиной l₁ определяем по формуле Дарси-Вейсбаха, Па:

Dр_тр = l₁ × × r × ,

где ₁— коэффициент гидравлического трения (коэффициент Дарси), безразмерный;

— длина трубопровода, м;

— диаметр трубопровода, м;

r — плотность жидкости, кг/м 3 ;

v₁ – средняя скорость течения жидкости в сечении потока, м/с.

Используя уравнение неразрывности течения определяем скорость на участке диаметром d₁, м/с:

v₁ = = = = = 0,0017 м/с.

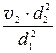
Определяем режим течения жидкости на участке трубопровода диаметром d₁ и длиной :

Re₁ = = = 3090,909.

Re > Re_кр = 2000…2320, следовательно режим движения турбулентный.

Для определения области сопротивления рассчитываем значение критерия зоны турбулентности:

Re × = 3090,909 × = 3,348.

Значение критерия зоны турбулентности меньше 10, следовательно движение происходит в области «гидравлически гладких» труб, для которой справедлива формула Блазиуса:

l₁ = = = 0,0424.

Потери давления на трение по длине равны:

Dр_тр = 0,0424 × × 965,3 × = 0,000394 (Па).

Потери давления на местных сопротивлениях определяем по формуле Вейсбаха, Па:

Dр_м = z × r × ,

где z – коэффициент местного сопротивления, безразмерный. При резких переходах в местных сопротивлениях коэффициент z не зависит от значения числа Рейнольдса при Re ³ 3000. Следовательно, при определении коэффициентов местного сопротивления мы можем использовать формулы для автомодельной области (3), (4), (10) – (16);

r – плотность жидкости, кг/м 3 ;

v – средняя скорость в сечении, обычно после местного сопротивления, м/с.

Однако при определении потерь энергии при расширении трубопровода расчёт принято проводить для скорости до местного сопротивления. В данном случае до местного сопротивления (внезапного расширения) диаметр d₂ и скорость v₂. Потери давления и коэффициент местного сопротивления, отнесённый к средней скорости до местного сопротивления, определяем по формулам (2) и (3), которые в данном случае записываются в виде:

Dр_{м в.р.} = z_в.р. × r ×

z_в.р. = ;

где w₂ — площадь трубопровода до расширения;

w₁ — площадь трубопровода после расширения.

z_в.р. = = = = 0,997.

Потери давления при внезапном расширении трубопровода равны, Па:

Dр_{м в.р.} = 0,997 × 965,3 × = 481,202.

II вариант (по потерянной скорости)

Если принять коэффициент Кориолиса a = 1, то потери давления можно определить по формуле Борда (5, б), Па:

Dр_в.р. = r × ,

где — скорость до местного сопротивления, м/с;

— скорость после местного сопротивления, м/с;

— потерянная скорость, м/с.

Dр_в.р. = 965,3 × = 481,01 (Па).

Потери давления при плавном повороте трубопровода на 180 0 определяем по формуле:

Dр_{м 180} = z₁₈₀ × r × .

Коэффициент сопротивления при плавном повороте трубопровода на Q = 180 0 определяем по формуле (15):

где а – справочный коэффициент, зависящий от угла поворота. При повороте на 180 0 а = 1,33;

z₉₀ – коэффициент местного сопротивления при плавном повороте трубы на 90 0 .

Коэффициент местного сопротивления при плавном повороте трубы на 90 0 определяем по эмпирической формуле Альтшуля (16):

z₉₀ = ,

где d₁ – диаметр нагревательной трубы, м;

R_п – радиус закругления трубы, м.

z₉₀ = = 104,654.

z_180. = 1,33 × 104,654 = 139,190.

Dр_{м 180} = 139,190×965,3 × = 0,194 (Па).

Потери давления при внезапном сужении трубопровода равны:

Dр_{м в.с.} = z_в.с. × r × .

Коэффициент местного сопротивления на внезапном сужении z_в.с определяем по формуле (10):

z_в.с. = .

Коэффициент сжатия струи e зависит оцениваем по эмпирической формуле (12):

e = 0,57 + .

Степень сжатия потока n равна:

n = = = = = 0,0017.

e = 0,57 + = 0,609.

z_в.с. = = 0,412.

Dр_{м в.с.} = 0,412 × 965,3 × = 198,852 (Па).

Общие потери давления в системе равны:

Dр_пот = 0,000394 + 481,202 + 0,194 + 198,852 = 680,2484 (Па).

Уравнение постоянства расхода

Уравнение постоянства расхода для потока жидкости

Гидродинамика — раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями.

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

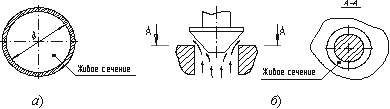
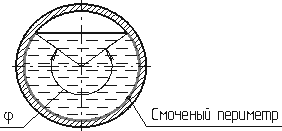
Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения. Например, живое сечение трубы — круг (рис.3.1, б); живое сечение клапана — кольцо с изменяющимся внутренним диаметром (рис.3.1, б).

Смоченный периметр χ («хи») — часть периметра живого сечения, ограниченное твердыми стенками (рис.3.2, выделен утолщенной линией).

Для круглой трубы

если угол в радианах, или

Расход потока Q — объем жидкости V, протекающей за единицу времени t через живое сечение ω.

Средняя скорость потока υ — скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Гидравлический радиус потока R — отношение живого сечения к смоченному периметру

Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока — трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением). Безнапорное — течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.п.). В данном курсе будет рассматриваться только напорное течение.

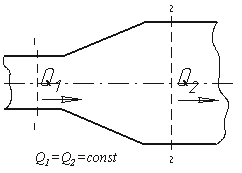
Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q₁=Q₂= const, откуда

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.

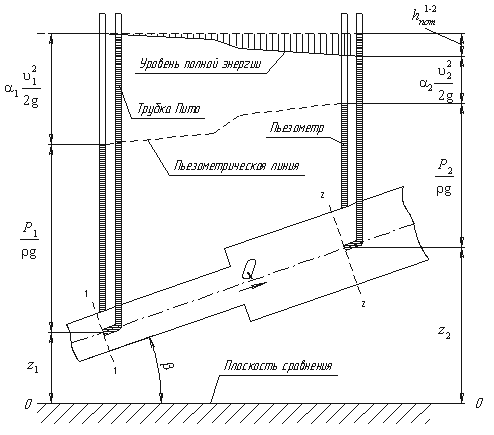
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.

Для измерения давления жидкости применяют пьезометры — тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту 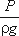. В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).

Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.

Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:

Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:

z1 и z2 — удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;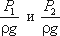
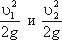
— удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
— удельные кинетические энергии в тех же сечениях.

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.

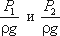
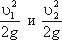
Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рис.3.5, можно заметить, что z1 и z2 — геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения; — пьезометрические высоты; — скоростные высоты в указанных сечениях.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α₁ и α₂, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).

Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

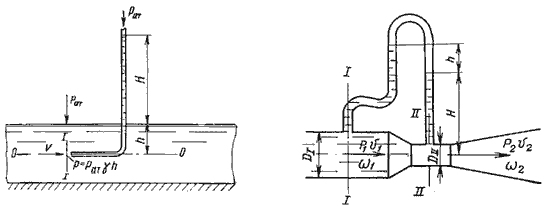
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

где Н — столб жидкости в трубке Пито.

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:

Выражение, стоящее перед 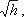, является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.