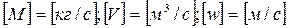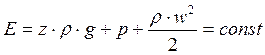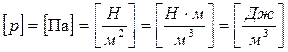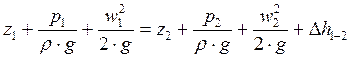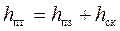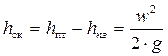Уравнение постоянства расхода и его физический смысл

Уравнение неразрывности и уравнение Бернулли.

Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.

Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.

Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости. Живое сечение может быть ограничено твердыми стенками полностью или частично. Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным.

Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.

Содержание статьи

Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.

Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным. Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υ_ср .

Таким образом уравнение расхода для потока будет

υ_ср – средняя скорость потока

F – площадь сечения потока.

Уравнение неразрывности потока жидкости

Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.

Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный

а через сечение 2-2 из него же вытекает объем, равный

Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.

Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.

Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки

Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что

т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.

Уравнение неразрывности струи жидкости. Уравнение Бернулли.

Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.

При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.

Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.

Если всё это записать в виде формулы, то

где W – приращение кинетической энергии = m * υ 2 / 2

ΣA – сумма работ действующих сил = P *ΔS

В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.

Теперь рассмотрим обе части этого выражения по порядку.

Приращение кинетической энергии ΔW

В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.

Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.

Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен

масса в этом случае получается равной

Подставляя все это в выражение для кинетической энергии получаем цепочку

ΔW = m * υ 2 ₂ / 2 — m * υ 2 ₁ / 2 = ρ * q * ΔТ * υ 2 ₂ / 2 — ρ * q * ΔТ * υ 2 ₁ / 2

Работа сил действующих на систему ΣA

Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести A_Т равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.

Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.

Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.

Силы давления А_Д , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.

Суммарно работа сил давления будет

Подставляя в начальное уравнение

Полученные выражения для ΔW и ΣA получаем

Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые

Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:

Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ ρ
Кинетическая удельная энергия = υ 2 / 2

В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Видео по теме уравнение неразрывности

Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.

Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.

Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.

Лекция по электроснабжение предприятий

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Тема: Основные уравнения движения

1. Уравнение неразрывности потока. Уравнение постоянства расхода

3. Уравнение Бернулли и его практическое применение

4. Дифференциальные уравнения движения идеальной и вязкой жидкости

5. Основные характеристики турбулентного движения

6. Подобие и моделирование гидромеханических процессов

1. Уравнение неразрывности потока. Уравнение постоянства расхода

Уравнение неразрывности элементарной струйки: скорости и площади поперечных сечений струек в различных живых сечениях могут меняться, однако произведение скорости отдельных частиц струйки на площади их поперечного сечения остаются постоянными

. (4.1)

Рассмотрим установившееся движение в русле переменного сечения (рисунок 4.1). Выберем два произвольных сечения I — I и II — II , нормальных к оси потока, и рассмотрим участок потока, заключённый между сечениями.

Рисунок 4.1 – Схема к уравнениям постоянства расхода и неразрывности потока

Так как жидкость несжимаема, а стенки русла жёсткие, то на основе второго свойства элементарной струйки можно записать уравнение постоянства расхода

. (4.2)

Уравнение постоянства расхода гласит: в любом сечении потока при установившемся движении несжимаемой жидкости её расход одинаков.

Так как , то получаем уравнение неразрывности потока

. (4.3)

Уравнение неразрывности потока гласит: при установившемся движении несжимаемой жидкости произведение средней скорости потока на площадь живого сечения является постоянной величиной.

Через сечения потока жидкости в единицу времени проходит одно и то же количество жидкости

. (4.4)

Из уравнения 4.4 следует, что средние скорости потока обратно пропорциональны площадям соответствующих сечений

или . (4.5)

Дифференциальное уравнение неразрывности имеет вид

, (4.6)

где — расход элементарной струйки;

— бесконечно малая площадь поперечного сечения струйки;

— скорость в поперечном сечении элементарной струйки.

Энергия – это физическая величина, которая показывает, какую работу, может совершить тело.

Известно, что механическая энергия любого тела характеризуется двумя величинами:

а) кинетической энергией (это энергия движения, зависящая от массы тела и скорости его движения)

, (4.7)

где — масса тела или частицы;

— скорость движения тела или частицы;

б) потенциальной энергией (это энергия, которая определяется взаимным расположением тел или частей одного тела).

Потенциальная энергия тела или частицы, поднятого на высоту

. (4.8)

Если масса жидкого тела занимает объём и находится под давлением , то это тело ещё обладает потенциальной энергией давления

. (4.9)

Полная механическая энергия элементарной струйки (частицы) определяется по формуле

, (4.10)

где — масса элементарной струйки (частицы);

— скорость элементарной струйки (частицы).

Удельная энергия струйки – это энергия, отнесённая к единице веса.

, (4.11)

где — удельная кинетическая энергия струйки;

— удельная потенциальная энергия струйки.

Так как поток жидкости представляет собой совокупность множества элементарных струек, и, принимая движение потока установившимся или плавно изменяющимся, можно определить удельную энергию потока жидкости конечных размеров.

Рассмотрим поток жидкости в виде наклонной трубы с плавно изменяющимся сечением (рисунок 4.2).

Рисунок 4.2 – Схема к выводу уравнения энергии потока жидкости

Внутри потока выделим некоторую точку . Обозначим расстояние от этой точки до произвольно выбранной плоскости (плоскость сравнения) — , давление жидкости в центре тяжести сечения — , среднюю скорость движения жидкости в выбранном сечении — .

Полная энергия потока будет равна

,

где — удельная кинетическая энергия потока;

— удельная потенциальная энергия.

Удельная кинетическая энергия определяется

, (4.12)

где — число элементарных струек;

— скорости элементарных струек;

— средняя скорость потока;

— коэффициент, учитывающий неравномерность распределения скорости по сечению.

Удельная потенциальная энергия согласно гидростатическому закону определяется

, (4.13)

то есть для всех точек данного объёма покоящейся жидкости удельная потенциальная энергия относительно выбранной плоскости сравнения постоянна.

Тогда полная удельная энергия потока в выбранном сечении примет вид

. (4.14)

Так как распределение скоростей в потоке неизвестно, то в механике жидкостей и газов эти скорости принимаются одинаковыми, а при определении кинетической энергии потока вводится поправочный коэффициент .

Поправочный коэффициент — коэффициент кинетической энергии (коэффициент Кориолиса) учитывает изменение кинетической энергии из-за неравномерного распределения скоростей в живом сечении потока.

— для равномерных турбулентных потоков.

— для равномерных ламинарных потоков.

3. Уравнение Бернулли и его практическое применение

В потоке жидкости, движущейся в трубке с плавно изменяющимся сечением (рисунок 4.3), выберем два произвольных сечения I — I и II — II . Обозначим и — давления в центрах тяжести сечений и , и — средние скорости, и — вертикальные координаты оси потока в выбранных сечениях.

Рисунок 4.3 – Схема к выводу уравнения Бернулли

Тогда величины полной удельной энергии потока в сечениях I и II соответственно могут быть записаны

. (4.15)

. (4.16)

При движении реальной жидкости часть энергии затрачивается на преодоление силы трения (сопротивления) на пути от первого сечения до второго. Эта энергия обращается в тепло и рассеивается.

Величину потерь обозначим .

Тогда баланс энергии в сечениях I и II (уравнение Бернулли для реального потока жидкости) можно записать

, (4.17)

, (4.18)

где — высота скоростного потока;

— пьезометрическая высота, отсчитываемая в каждом сечении по пьезометру;

— геометрическая высота;

— потерянный напор, равный части энергии, превращённой в тепло.

Уравнение Бернулли устанавливает математическую связь между основными элементами движения жидкости, то есть средней скоростью и гидродинамическим давлением. Оно показывает, что за счёт преобразования одного вида энергии в другой наблюдается при возрастании скорости и уменьшение давления и, наоборот, при уменьшении скорости – возрастание давления.

Физический (энергетический) смысл уравнения Бернулли состоит в том, что при установившемся движении жидкости сумма трёх удельных энергий (положения, давления и кинетической) остаётся неизменной.

Гидродинамический напор – это сумма скоростного напора, геометрической и пьезометрической высот

. (4.19)

На основании уравнения Бернулли сконструирован ряд приборов (водомер Вентури, водоструйный насос, эжектор и др.).

Рассмотрим применение уравнения Бернулли на примере водомерного устройства в трубах – водомера Вентури (рисунок 4.4), который представляет собой вставку в основную трубу диаметром трубы меньшего диаметра . Труба меньшего диаметра соединена с основной трубой коническими переходами.

В основной трубе (сечение I — I ) и в суженном сечении (сечение II — II ) присоединены пьезометры, по показаниям которых определяется расход жидкости в трубе.

Рисунок 4.4 – Схема водомера Вентури

Выведем общую формулу водомера для определения расхода жидкости.

Примем для заданных условий ; и ( из-за малости расстояния между сечениями). Составим уравнение Бернулли для точек, расположенных в центре тяжести сечений при плоскости сравнения О-О, проходящей по оси трубы

или .

Из рисунка 4.4 видно, что

→ .

В последнем уравнении неизвестны величины и . Применяя уравнение неразрывности, можно записать , откуда .

.

Скорость течения в основной трубе (сечение I — I ) равна

.

Так как , то .

Обозначим постоянную величину для данного водомера через :

, тогда ,

где — коэффициент, учитывающий потери напора в водомере, принимается равным 0,96…0,98.

Таким образом, зная диаметры водомера в расширенном и суженном сечениях, по разности давлений , измеряемой пьезометрами, можно легко определить расход воды.

В водоструйном насосе (рисунок 4.5) вода из бака 1 поступает в трубу, имеющую сужение. В узком сечении трубы скорость возрастает. При этом в соответствии с уравнением Бернулли давление здесь падает ниже атмосферного, поэтому происходит подсасывание жидкости по трубке, опущенной в бак 2. При больших скоростях движения жидкость будет подсасываться из бака 2 непрерывно.

Рисунок 7.5 – Схема водоструйного насоса

Скорость течения движущейся жидкости можно определить трубкой Пито . Этот прибор (рисунок 4.6) представляет собой стеклянную трубку, открытую с двух концов. При этом изогнутый под прямым углом конец трубки располагается в жидкости так, чтобы ось нижнего колена совпадала с линией тока.

Рисунок 4.6 – Схема прибора с трубкой Пито

В трубке Пито создаётся дополнительное давление от воздействия скорости движущейся жидкости (скоростной напор)

; ;

практически ,

где — коэффициент, зависящий от конструкции трубки и определяемый путём тарировки.

4. Дифференциальные уравнения движения идеальной и вязкой жидкости

Рассматриваемые уравнения представляют собой математическое выражение закона сохранения количества движения применительно к жидкому элементу: скорость изменения вектора количества движения равна сумме всех массовых и поверхностных сил, действующих на рассматриваемый жидкий элемент.

В качестве такого элемента используем жидкий прямоугольный параллелепипед с рёбрами (рисунок 4.7), на который действуют суммарный вектор поверхностных сил и вектор массовых сил, причём оба эти вектора отнесены к единице объёма.

Рисунок 4.7 – Схема к выводу дифференциальных уравнений движения идеальной жидкости

В данном случае рассматривается движение идеальной жидкости. Единственной поверхностной силой является сила, обусловленная гидродинамическим давлением .

На грани, перпендикулярные оси , будут действовать следующие силы: на левую грань — ; на правую грань — .

Учитывая принятое направление осей, получаем для поверхностей силы, отнесённой к единице объёма, действующей в направлении оси , .

Аналогично ; .

Уравнения движения идеальной жидкости (уравнения Эйлера) имеют вид

;

; (4.20)

.

Для плоского установившегося движения уравнения Эйлера имеют вид

;

. (4.21)

При одномерном течении (когда параметры потока и скорость зависят только от одной координаты) уравнение Эйлера имеет вид

. (4.22)

Уравнения движения, записанные с учётом сил вязкости, существенно усложняются. В отличие от идеальной жидкости поверхностные силы в общем случае направлены не нормально, а под произвольным углом к выделенной площадке.

Для вязкой жидкости уравнение движения (уравнение Навье-Стокса) имеет вид

;

; (4.23)

;

.

5. Основные характеристики турбулентного движения

Для турбулентного режима характерны перемешивание жидкости , пульсации скоростей и давлений в процессе движения. Поэтому механизм турбулентного потока очень сложен.

Движение жидкости становится турбулентным при достижении числом Рейнольдса критического значения. Тогда от стенок трубы отрываются отдельные жидкие массы, попадающие внутрь потока и своим перемещением нарушающие существовавшее до того упорядоченное (подслойное) движение.

В результате возникает диффузия образовавшихся у стенки вихрей, сопровождающаяся гашением заключённой в вихрях кинетической энергии турбулентности. При этом механическая энергия потока переходит частично в тепловую.

Из-за интенсивного вихреобразования частицы жидкости при турбулентном движении описывают весьма сложные траектории, а местные скорости не сохраняются постоянными даже в том случае, когда расход потока постоянен во времени.

Установившегося движения в турбулентном потоке не существует. В каждой точке потока скорость непрерывно меняется по величине и направлению.

Мгновенная местная скорость – это скорость в точке турбулентного потока.

Разложим мгновенную скорость на три взаимно перпендикулярных направления. Получим продольную составляющую , направленную по нормали к живому сечению, и две поперечные составляющие и , лежащие в плоскости живого сечения потока (рисунок 4.8).

Рисунок 4.8 – Составляющие пульсационных скоростей в турбулентном потоке

Как продольные, так и поперечные составляющие мгновенной скорости всё время меняются.

Пульсация скорости – это изменение во времени проекции мгновенной местной скорости на какое-либо направление. Пульсация скорости наблюдается с помощью чувствительных приборов. На рисунке 4.9 показан график пульсации.

Рисунок 4.9 – Пульсация мгновенной местной скорости в турбулентном потоке

Изменения скорости кажутся беспорядочными, но осреднённое за достаточно длинный промежуток времени значение скорости сохраняется постоянным. Это значит, что скорость непрерывно пульсирует около некоторого среднего (осреднённого во времени) значения .

Пульсировать – это подвергаться знакопеременным изменениям относительно какой-то средней величины.

Графически осреднённая скорость выражается высотой прямоугольника, равновеликого площади, заключённой между пульсационной кривой, осью абсцисс и двумя ординатами, соответствующими начальному и конечному моменту наблюдения. Для определения осреднённой скорости важно иметь достаточный период наблюдений, так как закономерной периодичности пульсационных кривых не обнаружено.

Осреднённая скорость – средняя скорость движения в данной точке, определяемая за достаточно продолжительный промежуток времени.

Пульсационная составляющая скорости (пульсационная добавка) – это разность между истинным и осреднённым значением местной скорости. Пульсационные добавки обозначаются теми же буквами, что и сами скорости, но со штрихом.

Пульсационная составляющая в продольном направлении имеет вид

. (4.24)

В турбулентном потоке вместо поля мгновенных скоростей можно рассматривать поле осреднённых скоростей. Только имея в виду осреднённые скорости, можно говорить об установившемся турбулентном движении.

Уравнение осреднённого движения турбулентного потока (уравнение Рейнольдса) имеет вид

, (4.25)

где — период наблюдений.

Также можно осреднить и другие компоненты скорости — и , а также любую другую быстро меняющуюся во времени величину, например произведение скоростей и , давление и другие.

Обычно рассматриваются не истинная, а только осреднённая скорость, а также поле осреднённых скоростей.

Вопросы для самопроверки

1 Как выглядит уравнение неразрывности элементарной струйки?

2 Какой вид имеет уравнение неразрывности потока и о чём оно гласит?

3 Что такое энергия?

4 Какими величинами характеризуется механическая энергия любого тела?

5 В чём заключается различие между кинетической и потенциальной энергиями?

6 Как определяется полная механическая энергия элементарной струйки?

7 Как определить удельную энергию струйки?

8 Чему равна полная энергия потока?

9 Как определить удельную кинетическую и удельную потенциальную энергии?

10 Чему равна полная удельная энергия потока?

11 Что учитывает коэффициент Кориолиса?

12 Какой вид имеет уравнение Бернулли для реального потока жидкости?

13 В чём заключается энергетический смысл уравнения Бернулли?

14 Что такое гидродинамический напор?

15 Как применяется уравнение Бернулли для водомера Вентури?

16 Практическое применение уравнения Бернулли на примере водоструйного насоса.

17 Что представляет собой трубка Пито?

18 Какой вид имеет дифференциальное уравнение движения идеальной жидкости?

19 как запишется уравнение Эйлера для плоского установившегося движения и одномерного течения?

20 какой вид имеет дифференциальное уравнение движения для вязкой жидкости?

21 Каковы основные характеристики турбулентного движения?

22 Дайте определение понятию мгновенной местной скорости.

23 Что такое пульсация скорости?

24 Что называется осреднённой скоростью и пульсационной составляющей скорости?

Уравнение постоянства расхода жидкости

При условии непроницаемости и недеформируемости стенок трубопровода и отсутствия разрывов и пустот для стационарного потока жидкости ее массовый расход постоянен.

– уравнение постоянства расхода жидкости.

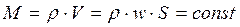
В любых поперечных сечениях стационарного потока жидкостей ее массовый расход постоянен.

Это уравнение выражается материальным балансом потока и является частным случаем закона сохранения массы.

. Отсюда следует,

– важное для практики следствие из уравнения постоянства расхода.

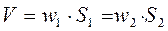
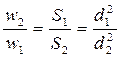
Средняя скорость обратно пропорциональна живому сечению потока или квадрату диаметра трубы.

Уравнение Бернулли

В 1738 году швейцарский ученый Д. Бернулли получил уравнение:

– уравнение Бернулли для стационарного потока идеальной (невязкой) жидкости

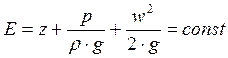
w – средняя скорость потока;

р – гидростатическое давление;

z – геометрический напор, т.е. удельная потенциальная энергия геометрического положения потока жидкости в данном сечении(м);

– статический или пьезометрический напор, т.е. удельная потенциальная энергия гидростатического давления жидкости на данном уровне (м) ;

– скоростной или динамический напор, т.е. удельная кинетическая энергия потока жидкости в данном сечении (м);

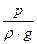
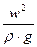
Е – полный гидродинамический напор, полная удельная механическая энергия потока жидкости в данном сечении.

В любых поперечных сечениях стационарного потока идеальной (невязкой) жидкости полный гидродинамический напор постоянен, т.е. полная удельная механическая энергия потока жидкости постоянна по длине труба.

Уравнение Бернулли выражает энергетический баланс потока и является частным случаем закона сохранения энергии.

Напор – удельная весовая механическая энергия потока жидкости.

Уравнение Бернулли можно записать иначе, если умножить обе его части на величину ρ·g:

р – механическая энергия единицы объема жидкости (потока).

Уравнение Бернулли можно применять для реальной (вязкой) жидкости:

Δh_1-2 – потеря напора потока на участке трубы между сечениями 1-1 и 2-2.

Потерянный напор расходуется на преодоление гидравлического сопротивления трубопровода. Последнее складывается из потерь на трение между слоями жидкости, между жидкостью и стенками трубы, а так же в местных сопротивлениях (резкий поворот трубы, внезапное изменение сечения потока, запорно-регулирующая арматура и т.д.).

При этом часть удельной потенциальной энергии жидкости превращается в тепловую энергию и рассеивается в окружающем пространстве.

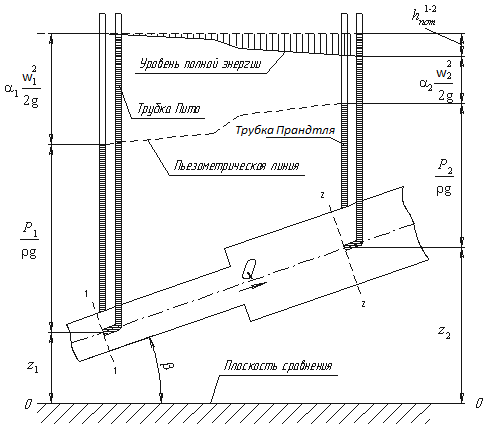
Рассмотрим диаграмму Бернулли:

Трубки Пито и Прандтля называют пьезометрическими. Иногда еще используют комбинированную трубку Пито-Прандтля.

Высота столбика жидкости в трубке Прандтля равна пьезометрическому напору:

.

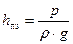
Высота столбика жидкости в трубке Пито равна сумме статического и скоростного напоров:

Отсюда, разность уровней столбиков жидкости в трубках Пито и Прандтля равна скоростному напору:

Если нижние концы трубок Пито и Прандтля находятся строго на оси трубы, то:

, таким образом, локальную скорость на оси трубы можно определить по показателям трубок Пито и Прандтля.

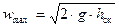
Имеется важное для практики следствие из уравнения Бернулли: при сужении потока часть удельной потенциальной энергии давления переходит в удельную кинематическую энергию потока жидкости, т.е. давление понижается, а скорость увеличивается; при расширении потока – все наоборот: скорость понижается, давление увеличивается.

Примеры практического применения уравнения Бернулли – насосы, компрессоры, дроссельные расходомеры, подъемная сила крыла самолета/птицы, эффект Магнуса и т.д.

Дата добавления: 2017-09-01 ; просмотров: 4027 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ