Уравнение поступательного прямолинейного равномерного движения

Равномерное прямолинейное движение

1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.

Равномерное движение — идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Реальное движение может лишь приближаться к равномерному движению с той или иной степенью точности.

2. Изменение положения тела в пространстве при равномерном движении может происходить с разной быстротой. Это свойство движения — его «быстрота» характеризуется физической величиной, называемой скоростью.

Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения ко времени, за которое это перемещение произошло.

Если за время ​ \( t \) ​ тело совершило перемещение ​ \( \vec \) ​, то скорость его движения ​ \( \vec \) ​ равна ​ \( \vec=\frac<\vec>\) ​.

Единица скорости: \( [\,v\,]=\frac<[\,s\,]> <[\,t\,]>\) ; \( [\,v\,]=\frac<1\,м><1\,с>=1\frac<м> <с>\) . За единицу скорости принимается 1 м/с — скорость такого равномерного движения, при котором тело за 1 с совершает перемещение 1 м.

Зная скорость равномерного движения, можно найти перемещение за любой промежуток времени: \( \vec=\vect \) . Вектор скорости и вектор перемещения направлены в одну сторону — в сторону движения тела.

3. Поскольку основной задачей механики является определение в любой момент времени положения тела, т.е. его координаты, необходимо записать уравнение зависимости координаты тела от времени при равномерном движении.

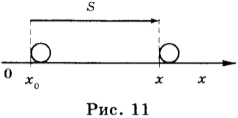
Пусть \( \vec \) — перемещение тела (рис. 11). Направим координатную ось ОХ по направлению перемещения. Найдем проекцию перемещения на координатную ось ОХ. На рисунке ​ \( x_0 \) ​ — координата начальной точки перемещения, ​ \( x \) ​ — координата конечной точки перемещения. Проекция перемещения равна разности координат конечной и начальной точек: ​ \( \vec_x=x-x_0 \) ​. С другой стороны, проекция перемещения равна проекции скорости, умноженной на время, т.е. \( \vec_x=\vec_xt \) . Откуда ​ \( x-x_0=\vec_xt \) ​ или \( x=x_0+\vec_xt \) . Если начальная координата ​ \( x_0 \) ​ = 0, то ​ \( x=\vec_xt \) ​.

Полученная формула позволяет определить координату тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.

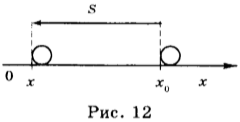
Проекция скорости может быть как положительной, так и отрицательной. Проекция скорости положительна, если направление движения совпадает с положительным направлением оси ОХ (рис. 12). В этом случае ​ \( x>x_0 \) ​. Проекция скорости отрицательна, если тело движется против положительного направления оси ОХ (рис. 12). В этом случае \( x .

4. Зависимость координаты от времени можно представить графически.

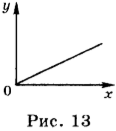
Предположим, что тело движется из начала координат вдоль положительного направления оси ОХ с постоянной скоростью. Проекция скорости на ось ОХ равна 4 м/с. Уравнение движения в этом случае имеет вид: ​ \( x \) ​ = 4 м/с · ​ \( t \) ​. Зависимость координаты от времени — линейная. Графиком такой зависимости является прямая линия, проходящая через начало координат (рис. 13).

Для того чтобы её построить, необходимо иметь две точки: одна из них ​ \( t \) ​ = 0 и ​ \( x \) ​ = 0, а другая ​ \( t \) ​ = 1 с, ​ \( x \) ​ = 4 м. На рисунке приведён график зависимости координаты от времени, соответствующий данному уравнению движения.

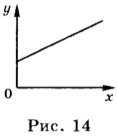
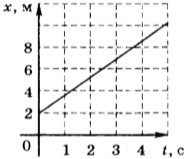
Если в начальный момент времени координата тела ​ \( x_0 \) ​ = 2 м, а проекция его скорости ​ \( v_x \) ​ = 4 м/с, то уравнение движения имеет вид: ​ \( x \) ​ = 2 м + 4 м/с · ​ \( t \) ​. Это тоже линейная зависимость координаты от скорости, и её графиком является прямая линия, проходящая через точку, для которой ​ \( t \) ​ = 0, ​ \( x \) ​ = 2 м (рис. 14).

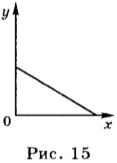
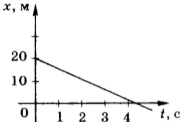
В том случае, если проекция скорости отрицательна, уравнение движения имеет вид: \( x \) ​ = 2 м – 4 м/с · ​ \( t \) ​. График зависимости координаты такого движения от времени представлен на рисунке 15.

Таким образом, движение тела может быть описано аналитически, т.е. с помощью уравнения движения (уравнения зависимости координаты тела от времени), и графически, т.е. с помощью графика зависимости координаты тела от времени.

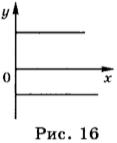
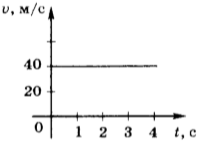
График зависимости проекции скорости равномерного прямолинейного движения от времени представлен на рисунке 16.

5. Ниже приведён пример решения основной задачи кинематики — определения положения тела в некоторый момент времени.

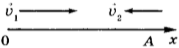
Задача. Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один со скоростью 15 м/с, другой — со скоростью 12 м/с. Определите время и место встречи автомобилей, если в начальный момент времени расстояние между ними равно 270 м.

При решении задачи целесообразно придерживаться следующей последовательности действий:

1. Кратко записать условие задачи.
2. Проанализировать ситуацию, описанную в условии задачи:
   — выяснить, можно ли принять движущиеся тела за материальные точки;
   — сделать рисунок, изобразив на нём векторы скорости;
   — выбрать систему отсчёта — тело отсчёта, направления координатных осей, начало отсчёта координат, начало отсчёта времени; записать начальные условия (значения координат в начальный момент времени) для каждого тела.
3. Записать в общем виде уравнение движения в векторной форме и для проекций на координатные оси.
4. Записать уравнение движения для каждого тела с учётом начальных условий и знаков проекций скорости.
5. Решить задачу в общем виде.
6. Подставить в формулу значения величин и выполнить вычисления.
7. Проанализировать ответ.

Применим эту последовательность действий к приведённой выше задаче.

Дано: ​ \( v_1 \) ​ = 15 м/с ​ \( v_2 \) ​= 12 м/с ​ \( l \) ​= 270 м. Найти: ​ \( t \) ​ – ? \( x\) ​ – ?

Автомобили можно считать материальными точками, поскольку расстояние между ними много больше их размеров и размерами автомобилей можно пренебречь

Система отсчёта связана с Землёй, ось ​ \( Ox \) ​ направлена в сторону движения первого тела, начало отсчёта координаты — т. ​ \( O \) ​ — положение первого тела в начальный момент времени.

Начальные условия: ​ \( t \) ​ = 0; ​ \( x_ <01>\) ​ = 0; \( x_ <02>\) = 270.

Уравнение в общем виде: ​ \( \vec=\vect \) ​; ​ \( x=x_0+v_xt \) .

Уравнения для каждого тела с учётом начальных условий: ​ \( x_1=v_1t \) ​; ​ \( x_2=l-v_2t \) ​. В месте встречи тел ​ \( x_1=x_2 \) ; следовательно: ​ \( v_1t=l-v_2t \) ​. Откуда ​ \( t=\frac\cdot t \) ​. Подставив значение времени в уравнение для координаты первого автомобиля, получим значение координаты места встречи автомобилей: ​ \( x \) ​ = 150 м.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?

1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с

2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?

1) 0,25 м
2) 6 м
3) 10 м
4) 150 м

3. Автомобиль «Рено» проезжает за 1 мин. путь 1,2 км. Автомобиль «Пежо» проезжает за 20 с путь 0,2 км. Сравните значения скорости «Рено» — ​ \( v_1 \) ​ и скорости «Пежо» — \( v_2 \) .

1) ​ \( v_1=v_2 \) ​
2) ​ \( v_1=2v_2 \) ​
3) \( 2v_1=v_2 \)
4) \( 1,2v_1=10v_2 \)

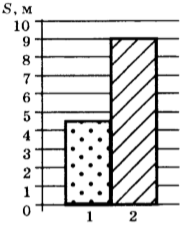
4. На рисунке приведена столбчатая диаграмма. На ней представлены значения пути, которые при равномерном движении пролетают за одно и то же время муха (1) и воробей (2). Сравните их скорости ​ \( v_1 \) ​ и \( v_2 \) .

1) ​ \( v_1=v_2 \) ​
2) ​ \( v_1=2v_2 \) ​
3) \( 3v_1=v_2 \)
4) \( 2v_1=v_2 \)

5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен

1) 20 м
2) 40 м
3) 80 м
4) 160 м

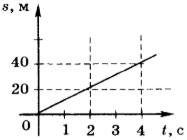
6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен

1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с

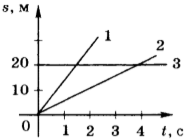
7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости ​ \( v_1 \) ​, \( v_2 \) и \( v_3 \) движения этих тел.

1) ​ \( v_1=v_2=v_3 \) ​
2) \( v_1>v_2>v_3 \) ​
3) \( v_1 ​
4) ​ \( v_1=v_2 \) , \( v_3

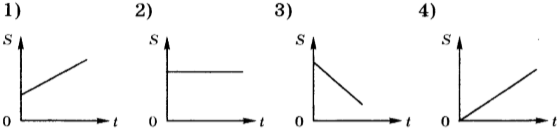
8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?

9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?

1) 9,8 м
2) 6 м
3) 4 м
4) 2 м

10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид

1) ​ \( x=1t \) ​ (м)
2) \( x=2+3t \) (м)
3) \( x=2-1t \) (м)
4) \( x=4+2t \) (м)

11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость

ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит

12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.

1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось

Часть 2

13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?

Уравнение поступательного прямолинейного равномерного движения

лЙОЕНБФЙЛБ ЙЪХЮБЕФ ТБЪМЙЮОЩЕ НЕИБОЙЮЕУЛЙЕ ДЧЙЦЕОЙС ФЕМ ВЕЪ ТБУУНПФТЕОЙС РТЙЮЙО ЧЩЪЩЧБАЭЙИ ЬФЙ ДЧЙЦЕОЙС.

1.1.1 лЙОЕНБФЙЛБ РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС

рТЙ РПУФХРБФЕМШОПН ДЧЙЦЕОЙЙ ФЕМБ ЧУЕ ФПЮЛЙ ФЕМБ ДЧЙЦХФУС ПДЙОБЛПЧП, Й, ЧНЕУФП ФПЗП ЮФПВЩ ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ЛБЦДПК ФПЮЛЙ ФЕМБ, НПЦОП ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ФПМШЛП ПДОПК ЕЗП ФПЮЛЙ.

пУОПЧОЩЕ ИБТБЛФЕТЙУФЙЛЙ ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ: ФТБЕЛФПТЙС ДЧЙЦЕОЙС, РЕТЕНЕЭЕОЙЕ ФПЮЛЙ, РТПКДЕООЩК ЕА РХФШ, ЛППТДЙОБФЩ, УЛПТПУФШ Й ХУЛПТЕОЙЕ.

мЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ Ч РТПУФТБОУФЧЕ, ОБЪЩЧБАФ ФТБЕЛФПТЙЕК.

рЕТЕНЕЭЕОЙЕН НБФЕТЙБМШОПК ФПЮЛЙ ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ОБЪЩЧБЕФУС ЧЕЛФПТ РЕТЕНЕЭЕОЙС &#8710r=r-r₀, ОБРТБЧМЕООЩК ПФ РПМПЦЕОЙС ФПЮЛЙ Ч ОБЮБМШОЩК НПНЕОФ ЧТЕНЕОЙ Л ЕЕ РПМПЦЕОЙА Ч ЛПОЕЮОЩК НПНЕОФ.

уЛПТПУФШ НБФЕТЙБМШОПК ФПЮЛЙ РТЕДУФБЧМСЕФ УПВПК ЧЕЛФПТ, ИБТБЛФЕТЙЪХАЭЙК ОБРТБЧМЕОЙЕ Й ВЩУФТПФХ РЕТЕНЕЭЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ. чЕЛФПТ ХУЛПТЕОЙС ИБТБЛФЕТЙЪХЕФ ВЩУФТПФХ Й ОБРТБЧМЕОЙЕ ЙЪНЕОЕОЙС УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ.

1.1.2 тБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ

тБЧОПНЕТОЩН РТСНПМЙОЕКОЩН ДЧЙЦЕОЙЕН ОБЪЩЧБЕФУС ФБЛПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ, РТЙ ЛПФПТПН НБФЕТЙБМШОБС ФПЮЛБ (ФЕМП) ДЧЙЦЕФУС РП РТСНПК Й Ч МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ УПЧЕТЫБЕФ ПДЙОБЛПЧЩЕ РЕТЕНЕЭЕОЙС.

чЕЛФПТ УЛПТПУФЙ ТБЧОПНЕТОПЗП РТСНПМЙОЕКОПЗП ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ОБРТБЧМЕО ЧДПМШ ЕЕ ФТБЕЛФПТЙЙ Ч УФПТПОХ ДЧЙЦЕОЙС. чЕЛФПТ УЛПТПУФЙ РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ ТБЧЕО ЧЕЛФПТХ РЕТЕНЕЭЕОЙС ЪБ МАВПК РТПНЕЦХФПЛ ЧТЕНЕОЙ, РПДЕМЕООПНХ ОБ ЬФПФ РТПНЕЦХФПЛ ЧТЕНЕОЙ:

рТЙНЕН МЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ, ЪБ ПУШ ЛППТДЙОБФ пи, РТЙЮЕН ЪБ РПМПЦЙФЕМШОПЕ ОБРТБЧМЕОЙЕ ПУЙ ЧЩВЕТЕН ОБРТБЧМЕОЙЕ ДЧЙЦЕОЙС ФПЮЛЙ. фПЗДБ, УРТПЕГЙТПЧБЧ ЧЕЛФПТЩ r Й v, ОБ ЬФХ ПУШ, ДМС РТПЕЛГЙК ∆r_x = |∆r| Й ∆v_x = |∆v| ЬФЙИ ЧЕЛФПТПЧ НЩ НПЦЕН ЪБРЙУБФШ:

, ПФУАДБ РПМХЮБЕН ХТБЧОЕОЙЕ ТБЧОПНЕТОПЗП ДЧЙЦЕОЙС: ∆r_x = v_x · t .

ф.Л. РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ S = |∆r|, НПЦЕН ЪБРЙУБФШ: S_x = v_x · t. фПЗДБ ДМС ЛППТДЙОБФЩ ФЕМБ Ч МАВПК НПНЕОФ ЧТЕНЕОЙ ЙНЕЕН:

ЗДЕ И₀ — ЛППТДЙОБФБ ФЕМБ Ч ОБЮБМШОЩК НПНЕОФ t = 0.

рТЙНЕТ 1. хТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ДБОП Ч ЧЙДЕ И = 4 — 3t. пРТЕДЕМЙФШ ОБЮБМШОХА ЛППТДЙОБФХ ФЕМБ, УЛПТПУФШ ДЧЙЦЕОЙС Й РЕТЕНЕЭЕОЙС ФЕМБ ЪБ 2 УЕЛХОДЩ.

тЕЫЕОЙЕ: уТБЧОЙН ДБООПЕ ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ У ХТБЧОЕОЙЕН ДЧЙЦЕОЙС Ч ПВЭЕН ЧЙДЕ: И = И₀ + v_x t Й И = 4 — 3t.

пЮЕЧЙДОП, ЮФП И₀ = 4Н, v_x = — 3Н/У (ЪОБЛ «-» ПЪОБЮБЕФ, ЮФП ОБРТБЧМЕОЙЕ УЛПТПУФЙ ОЕ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ПУЙ пи, Ф.Е. ПОЙ РТПФЙЧПРПМПЦОП ОБРТБЧМЕОЩ). рЕТЕНЕЭЕОЙЕ ФЕМБ ОБКДЕН РП ЖПТНХМЕ: S = И — И₀. лПОЕЮОХА ЛППТДЙОБФХ И НПЦОП ПРТЕДЕМЙФШ, РПДУФБЧМСС Ч ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ЧТЕНС t₁: И = 4 — 3t₁. ч ПВЭЕН ЧЙДЕ ЖПТНХМБ РЕТЕНЕЭЕОЙС: S = 4 — 3t₁ — И₀ = 4 — 3t₁ — 4 = — 3t₁ = -3 · 2 = — 6 Н (фЕМП ДЧЙЦЕФУС Ч ПФТЙГБФЕМШОПН ОБРТБЧМЕОЙЙ ПУЙ пи).

рТЙНЕТ 2.мПДПЮОЙЛ РЕТЕЧПЪЙФ РБУУБЦЙТПЧ У ПДОПЗП ВЕТЕЗБ ОБ ДТХЗПК ЪБ ЧТЕНС t =10 НЙО. РП ФТБЕЛФПТЙЙ бч. уЛПТПУФШ ФЕЮЕОЙС ТЕЛЙ vТ = 0,3 Н/У, ЫЙТЙОБ ТЕЛЙ 240 Н. у ЛБЛПК УЛПТПУФША v ПФОПУЙФЕМШОП ЧПДЩ Й РПД ЛБЛЙН ХЗМПН α Л ВЕТЕЗХ ДПМЦОБ ДЧЙЗБФШУС МПДЛБ, ЮФПВЩ ДПУФЙЮШ ДТХЗПЗП ВЕТЕЗБ ЪБ ХЛБЪБООПЕ ЧТЕНС?

t = 10 НЙО = 660 У.

v’ — ? α — ?

тЕЫЕОЙЕ: рТЙНЕН ВЕТЕЗ ЪБ ОЕРПДЧЙЦОХА УЙУФЕНХ ПФУЮЕФБ. фПЗДБ ПФОПУЙФЕМШОП ВЕТЕЗБ УЛПТПУФШ МПДЛЙ ТБЧОБ:

ьФБ УЛПТПУФШ (ТЙУХОПЛ 1.1), СЧМСЕФУС УХННПК ДЧХИ УЛПТПУФЕК: УЛПТПУФЙ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ v’ (УЛПТПУФЙ ПФОПУЙФЕМШОП РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ) Й УЛПТПУФЙ ТЕЛЙ v_Т (УЛПТПУФЙ УБНПК РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ ПФОПУЙФЕМШОП ОЕРПДЧЙЦОПК). рП ЪБЛПОХ УМПЦЕОЙС УЛПТПУФЕК: v =v_Т + v’. фБЛ ЛБЛ РП ХУМПЧЙА ЪБДБЮЙ УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ВЕТЕЗБ ОБРТБЧМЕОБ ЧДПМШ бч, Б УЛПТПУФШ ТЕЛЙ РЕТРЕОДЙЛХМСТОП бч, ФП УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ(РП ФЕПТЕНЕ рЙЖБЗПТБ):

йУЛПНЩК ХЗПМ НПЦОП ОБКФЙ ЙЪ ЧЩТБЦЕОЙС:

пФЧЕФ: v’ = 0.5 Н /У, α = arctg ≈ 53 0 .

1.1.3 оЕТБЧОПНЕТОПЕ ДЧЙЦЕОЙЕ

дЧЙЦЕОЙЕ, РТЙ ЛПФПТПН ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ФЕМП УПЧЕТЫБЕФ ОЕТБЧОЩЕ РЕТЕНЕЭЕОЙС ОБЪЩЧБАФ ОЕТБЧОПНЕТОЩН ЙМЙ РЕТЕНЕООЩН. уТЕДОЕК УЛПТПУФША v_УТ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА РЕТЕНЕЭЕОЙС ФЕМБ ∆r ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ЬФПНХ РТПНЕЦХФЛХ:

нПДХМШ УТЕДОЕК УЛПТПУФЙ ПРТЕДЕМСЕФУС ЛБЛ ПФОПЫЕОЙЕ РХФЙ ∆S, РТПКДЕООПЗП ФЕМПН ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ, Л ЬФПНХ РТПНЕЦХФЛХ:

оБРТБЧМЕОЙЕ ЧЕЛФПТБ УТЕДОЕК УЛПТПУФЙ v_УТ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ∆r (ТЙУХОПЛ 1.2).

рТЙ ОЕПЗТБОЙЮЕООПН ХНЕОШЫЕОЙЙ ∆t, v_УТ УФТЕНЙФУС Л РТЕДЕМШОПНХ ЪОБЮЕОЙА, ЛПФПТПЕ ОБЪЩЧБЕФУС НЗОПЧЕООПК УЛПТПУФША. йФБЛ, НЗОПЧЕООБС УЛПТПУФШ v ЕУФШ РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС УЛПТПУФШ v_УТ, ЛПЗДБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ДЧЙЦЕОЙС УФТЕНЙФУС Л ОХМА:

йЪ ЛХТУБ НБФЕНБФЙЛЙ ЙЪЧЕУФОП, ЮФП РТЕДЕМ ПФОПЫЕОЙС РТЙТБЭЕОЙС ЖХОЛГЙЙ Л РТЙТБЭЕОЙА БТЗХНЕОФБ, ЛПЗДБ РПУМЕДОЙК УФТЕНЙФУС Л ОХМА РТЕДУФБЧМСЕФ УПВПК РЕТЧХА РТПЙЪЧПДОХА ЬФПК ЖХОЛГЙЙ РП ДБООПНХ БТЗХНЕОФХ. рПЬФПНХ:

нЗОПЧЕООБС УЛПТПУФШ v ЕУФШ ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС РЕТЧПК РТПЙЪЧПДОПК ТБДЙХУБ — ЧЕЛФПТБ ДЧЙЦХЭЕКУС ФПЮЛЙ РП ЧТЕНЕОЙ. фБЛ ЛБЛ УЕЛХЭБС Ч РТЕДЕМЕ УПЧРБДБЕФ У ЛБУБФЕМШОПК, ФП ЧЕЛФПТ УЛПТПУФЙ v ОБРТБЧМЕО РП ЛБУБФЕМШОПК Л ФТБЕЛФПТЙЙ Ч УФПТПОХ ДЧЙЦЕОЙС (ТЙУХОПЛ 1.2).

рП НЕТЕ ХНЕОШЫЕОЙЕ ∆t РХФШ ∆S ЧУЕ ВПМШЫЕ ВХДЕФ РТЙВМЙЦБФШУС Л |∆r|, РПЬФПНХ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ:

фБЛЙН ПВТБЪПН, НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ v ТБЧЕО РЕТЧПК РТПЙЪЧПДОПК РХФЙ РП ЧТЕНЕОЙ :

рТЙ ОЕТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФЕМБ ЕЗП УЛПТПУФШ ОЕРТЕТЩЧОП ЙЪНЕОСЕФУС. лБЛ ВЩУФТП ЙЪНЕОСЕФУС УЛПТПУФШ ФЕМБ, РПЛБЪЩЧБЕФ ЧЕМЙЮЙОБ, ЛПФПТБС ОБЪЩЧБЕФУС ХУЛПТЕОЙЕН. уТЕДОЙН ХУЛПТЕОЙЕН ОЕТБЧОПНЕТОПЗП ДЧЙЦЕОЙС Ч ЙОФЕТЧБМЕ ПФ t ДП t + ∆t ОБЪЩЧБЕФУС ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА ЙЪНЕОЕОЙС УЛПТПУФЙ ∆v Л ЙОФЕТЧБМХ ЧТЕНЕОЙ ∆t:

нЗОПЧЕООЩН ХУЛПТЕОЙЕН Б Ч НПНЕОФ ЧТЕНЕОЙ t ВХДЕФ РТЕДЕМ УТЕДОЕЗП ХУЛПТЕОЙС:

фБЛЙН ПВТБЪПН, ХУЛПТЕОЙЕ ∆Б ЕУФШ ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС РЕТЧПК РТПЙЪЧПДОПК УЛПТПУФЙ РП ЧТЕНЕОЙ. ч ДБООПК УЙУФЕНЕ ПФУЮЕФБ ЧЕЛФПТ ХУЛПТЕОЙС НПЦЕФ ВЩФШ ЪБДБО РТПЕЛГЙСНЙ ОБ УППФЧЕФУФЧХАЭЙЕ ЛППТДЙОБФОЩЕ ПУЙ (РТПЕЛГЙСНЙ Б_И, Б_Х, Б_z).

уПУФБЧМСАЭБС Б_τ ЧЕЛФПТБ ХУЛПТЕОЙС, ОБРТБЧМЕООБС ЧДПМШ ЛБУБФЕМШОПК Л ФТБЕЛФПТЙЙ Ч ДБООПК ФПЮЛЕ, ОБЪЩЧБЕФУС ФБОЗЕОГЙБМШОЩН (ЛБУБФЕМШОЩН) ХУЛПТЕОЙЕН. фБОЗЕОГЙБМШОПЕ ХУЛПТЕОЙЕ ИБТБЛФЕТЙЪХЕФ ЙЪНЕОЕОЙЕ ЧЕЛФПТБ УЛПТПУФЙ РП НПДХМА. чЕЛФПТ Б_τ ОБРТБЧМЕО Ч УФПТПОХ ДЧЙЦЕОЙС ФПЮЛЙ РТЙ ЧПЪТБУФБОЙЙ ЕЕ УЛПТПУФЙ (ТЙУХОПЛ 1.3 — Б) Й Ч РТПФЙЧПРПМПЦОХА УФПТПОХ — РТЙ ХВЩЧБОЙЙ УЛПТПУФЙ (ТЙУХОПЛ 1.3 — В).

фБОЗЕОГЙБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС Б_τ ТБЧОБ РЕТЧПК РТПЙЪЧПДОПК РП ЧТЕНЕОЙ ПФ НПДХМС УЛПТПУФЙ, ПРТЕДЕМСС ФЕН УБНЩН ВЩУФТПФХ ЙЪНЕОЕОЙС УЛПТПУФЙ РП НПДХМА:

чФПТБС УПУФБЧМСАЭБС ХУЛПТЕОЙС, ТБЧОБС:

ОБЪЩЧБЕФУС ОПТНБМШОПК УПУФБЧМСАЭЕК ХУЛПТЕОЙС Й ОБРТБЧМЕОБ РП ОПТНБМЙ Л ФТБЕЛФПТЙЙ Л ГЕОФТХ ЕЕ ЛТЙЧЙЪОЩ (РПЬФПНХ ЕЕ ОБЪЩЧБАФ ФБЛ ЦЕ ГЕОФТПУФТЕНЙФЕМШОЩН ХУЛПТЕОЙЕН).

рПМОПЕ ХУЛПТЕОЙЕ ЕУФШ ЗЕПНЕФТЙЮЕУЛБС УХННБ ФБОЗЕОГЙБМШОПК Й ОПТНБМШОПК УПУФБЧМСАЭЙИ:

рТЙНЕТ 1. рХУФШ И ЧПЪТБУФБЕФ РТПРПТГЙПОБМШОП ЛЧБДТБФХ ЧТЕНЕОЙ, Ф.Е. И = б·t 2 . юЕНХ ТБЧОБ НЗОПЧЕООБС УЛПТПУФШ Ч НПНЕОФ ЧТЕНЕОЙ t₁ — ?

тЕЫЕОЙЕ: ч ПВЭЕН УМХЮБЕ РТПЙЪЧПДОБС ПФ УФЕРЕООПК ЖХОЛГЙЙ t n ЪБРЙУЩЧБЕФУС Ч ЧЙДЕ:

нЗОПЧЕООБС УЛПТПУФШ ПРТЕДЕМСЕФУС:

пФЧЕФ: ч НПНЕОФ ЧТЕНЕОЙ t₁ ЙНЕЕН v = 2·Б·t₁.

рТЙНЕТ 2. ъБЧЙУЙНПУФШ РТПКДЕООПЗП ФЕМПН РХФЙ S ПФ ЧТЕНЕОЙ t ЪБДБЕФУС ХТБЧОЕОЙЕН S = At — Bt 2 + Ct 3 , ЗДЕ б = 2 Н/У, ч = 3 Н/У 2 , у = 4 Н/У 3 .

оБКФЙ: Б) ЪБЧЙУЙНПУФШ УЛПТПУФЙ v Й ХУЛПТЕОЙС a ФЕМБ ПФ ЧТЕНЕОЙ t;

В) ТБУУФПСОЙЕ S, УЛПТПУФШ v Й ХУЛПТЕОЙЕ Б ФЕМБ ЮЕТЕЪ ЧТЕНС t =2 У РПУМЕ ОБЮБМБ ДЧЙЦЕОЙС.

S = At — Bt 2 + Ct 3 , б = 2 Н/У, ч = 3 Н/У 2 , у = 4 Н/У 3 ;

В) S -? , V -? , a-? РТЙ t = 2 c.

Б) уЛПТПУФШ ФЕМБ: v = ds /dt ; v = A — 2Bt + 3Ct 2 ; v = 2 — 6t + 12t 2 Н/У. хУЛПТЕОЙЕ ФЕМБ: Б = dv /dt; Б= — 2B + 6уt; a = — 6 + 24t Н/У 2 .

В) тБУУФПСОЙЕ, РТПКДЕООПЕ ФЕМПН, S = 2t — 3t 2 + 4t 3 . фПЗДБ ЮЕТЕЪ ЧТЕНС t = 2c ЙНЕЕН: S = 24 Н; v = 38 Н/У; Б = 42 Н/У 2 .

пФЧЕФ: v = 2 — 6t + 12t 2 ; a = — 6 + 24 t Н/У 2 ; S = 24 Н; v = 38 Н/У; Б = 42 Н/У 2 .

1.1.4 тБЧОПРЕТЕНЕООПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ

тБЧОПРЕТЕНЕООЩН ОБЪЩЧБЕФУС ДЧЙЦЕОЙЕ, РТЙ ЛПФПТПН УЛПТПУФШ ФЕМБ (НБФЕТЙБМШОПК ФПЮЛЙ) ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ЙЪНЕОСЕФУС ПДЙОБЛПЧП, Ф.Е. ОБ ТБЧОЩЕ ЧЕМЙЮЙОЩ. ьФП ДЧЙЦЕОЙЕ НПЦЕФ ВЩФШ ТБЧОПХУЛПТЕООЩН Й ТБЧОПЪБНЕДМЕООЩН.

еУМЙ ОБРТБЧМЕОЙЕ ХУЛПТЕОЙС Б УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН УЛПТПУФЙ v ФПЮЛЙ, ДЧЙЦЕОЙЕ ОБЪЩЧБЕФУС ТБЧОПХУЛПТЕООЩН. еУМЙ ОБРТБЧМЕОЙЕ ЧЕЛФПТПЧ Б Й v РТПФЙЧПРПМПЦОЩ, ДЧЙЦЕОЙЕ ОБЪЩЧБЕФУС ТБЧОПЪБНЕДМЕООЩН.

рТЙ ТБЧОПРЕТЕНЕООПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ ХУЛПТЕОЙЕ ПУФБЕФУС РПУФПСООЩН Й РП НПДХМА Й РП ОБРТБЧМЕОЙА (Б = const). рТЙ ЬФПН УТЕДОЕЕ ХУЛПТЕОЙЕ Б_УТ ТБЧОП НЗОПЧЕООПНХ ХУЛПТЕОЙА Б ЧДПМШ ФТБЕЛФПТЙЙ ФПЮЛЙ. оПТНБМШОПЕ ХУЛПТЕОЙЕ РТЙ ЬФПН ПФУХФУФЧХЕФ ( Б_n=0 ).

йЪНЕОЕОЙЕ УЛПТПУФЙ ∆v = v — v₀ Ч ФЕЮЕОЙЙ РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t = t — t₀ РТЙ ТБЧОПРЕТЕНЕООПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ ТБЧОП: ∆v = a·∆t, ЙМЙ v — v₀ = a·(t — t₀). еУМЙ Ч НПНЕОФ ОБЮБМБ ПФУЮЕФБ ЧТЕНЕОЙ (t₀) УЛПТПУФШ ФПЮЛЙ ТБЧОБ v₀ (ОБЮБМШОБС УЛПТПУФШ) Й ХУЛПТЕОЙЕ Б ЙЪЧЕУФОП, ФП УЛПТПУФШ v Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t: v = v₀ + a·t. рТПЕЛГЙС ЧЕЛФПТБ УЛПТПУФЙ ОБ ПУШ пи УЧСЪБОБ У УППФЧЕФУФЧХАЭЙНЙ РТПЕЛГЙСНЙ ЧЕЛФПТПЧ ОБЮБМШОПК УЛПТПУФЙ Й ХУЛПТЕОЙС ХТБЧОЕОЙЕН: v_И = v_0И ± a_И·t. бОБМПЗЙЮОП ЪБРЙУЩЧБАФУС ХТБЧОЕОЙС ДМС РТПЕЛГЙК ЧЕЛФПТБ УЛПТПУФЙ ОБ ДТХЗЙЕ ЛППТДЙОБФОЩЕ ПУЙ.

чЕЛФПТ РЕТЕНЕЭЕОЙС ∆r ФПЮЛЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t₀ РТЙ ТБЧОПРЕТЕНЕООПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ У ОБЮБМШОПК УЛПТПУФША v₀ Й ХУЛПТЕОЙЕН Б ТБЧЕО:

Б ЕЗП РТПЕЛГЙС ОБ ПУШ пи (ЙМЙ РЕТЕНЕЭЕОЙЕ ФПЮЛЙ ЧДПМШ УППФЧЕФУФЧХАЭЕК ПУЙ ЛППТДЙОБФ) РТЙ t₀ = 0 ТБЧОБ:

рХФШ S_x, РТПКДЕООЩК ФПЮЛПК ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t₀ Ч ТБЧОПРЕТЕНЕООПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ У ОБЮБМШОПК УЛПТПУФША v₀ Й ХУЛПТЕОЙЕН Б, РТЙ t₀ = 0 ТБЧЕО:

фБЛ ЛБЛ ЛППТДЙОБФБ ФЕМБ ТБЧОБ И = И₀ + S, ФП ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ЙНЕЕФ ЧЙД:

чПЪНПЦОП ФБЛ ЦЕ РТЙ ТЕЫЕОЙЙ ЪБДБЮ ЙУРПМШЪПЧБФШ ЖПТНХМХ:

рТЙНЕТ 1. хУЛПТЕОЙЕ БЧФПНПВЙМС ТБЧОП Б = — 4 Н/У₂. юФП ЬФП ПЪОБЮБЕФ?

тЕЫЕОЙЕ: хУЛПТЕОЙЕ БЧФПНПВЙМС ПФТЙГБФЕМШОП, УМЕДПЧБФЕМШОП, УЛПТПУФШ ЕЗП ХНЕОШЫБЕФУС, Ф.Е. БЧФПНПВЙМШ ФПТНПЪЙФ. еЗП УЛПТПУФШ ХНЕОШЫБЕФУС ОБ 4 Н/У ЪБ ЛБЦДХА УЕЛХОДХ.

рТЙНЕТ 2. дЧБ ЧЕМПУЙРЕДЙУФБ ЕДХФ ОБЧУФТЕЮХ ДТХЗ ДТХЗХ. пДЙО, ЙНЕС УЛПТПУФШ 18 ЛН/Ю, ДЧЙЦЕФУС ТБЧОПЪБНЕДМЕООП, У ХУЛПТЕОЙЕН 20 УН/У 2 , ДТХЗПК, ЙНЕС УЛПТПУФШ 5,4 ЛН/Ю, ДЧЙЦЕФУС ТБЧОПХУЛПТЕООП У ХУЛПТЕОЙЕН 0,2 Н/У 2 . юЕТЕЪ ЛБЛПЕ ЧТЕНС ЧЕМПУЙРЕДЙУФЩ ЧУФТЕФСФУС Й ЛБЛПЕ РЕТЕНЕЭЕОЙЕ УПЧЕТЫЙФ ЛБЦДЩК ЙЪ ОЙИ ДП ЧУФТЕЮЙ, ЕУМЙ ТБУУФПСОЙЕ НЕЦДХ ОЙНЙ Ч ОБЮБМШОЩК НПНЕОФ ЧТЕНЕОЙ 130 Н?

v₀₁ = 18 ЛН/Ю = 5 Н/У,

a₁ = 20 УН/У 2 = 0,2 Н/У 2 ,

Б)	В)
тЕЫЕОЙЕ: рХУФШ ПУШ пи УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ДЧЙЦЕОЙС РЕТЧПЗП ЧЕМПУЙРЕДЙУФБ, Б ОБЮБМП ЛППТДЙОБФ У ФПЮЛПК O, Ч ЛПФПТПК ПО ОБИПДЙМУС Ч НПНЕОФ ЧТЕНЕОЙ t = 0 (ТЙУХОПЛ 1.4). фПЗДБ ХТБЧОЕОЙС ДЧЙЦЕОЙС ЧЕМПУЙРЕДЙУФБ ФБЛПЧЩ : (Ф.Л. Б1И= — Б1; И01 = 0); (Ф.Л. v2x = — v02 Й a2x = — a2). ч НПНЕОФ ЧУФТЕЮЙ Ч ФПЮЛЕ б: t = t1; x1 = x2. фПЗДБ РПМХЮЙН ТБЧЕОУФЧП: , ПФЛХДБ v01·t1 + v02·t1 = И02, Ф.Л. Б1 = Б2, пРТЕДЕМЙН РЕТЕНЕЭЕОЙЕ ЛБЦДПЗП ДП ЧУФТЕЮЙ. 1.1.5 уЧПВПДОПЕ РБДЕОЙЕ ФЕМ. дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП ЧЕТФЙЛБМШОП ЧЧЕТИ уЧПВПДОЩН РБДЕОЙЕН ОБЪЩЧБЕФУС ДЧЙЦЕОЙЕ, ЛПФПТПЕ УПЧЕТЫЙМП ВЩ ФЕМП ФПМШЛП РПД ДЕКУФЧЙЕН УЙМЩ ФСЦЕУФЙ ВЕЪ ХЮЕФБ УПРТПФЙЧМЕОЙС ЧПЪДХИБ. рТЙ УЧПВПДОПН РБДЕОЙЙ ФЕМБ У ОЕВПМШЫПК ЧЩУПФЩ h ПФ РПЧЕТИОПУФЙ ъЕНМЙ (h ≪RЪ, ЗДЕ RЪ — ТБДЙХУ ъЕНМЙ) ПОП ДЧЙЦЕФУС У РПУФПСООЩН ХУЛПТЕОЙЕН g, ОБРТБЧМЕООЩН ЧЕТФЙЛБМШОП ЧОЙЪ. хУЛПТЕОЙЕ g ОБЪЩЧБЕФУС ХУЛПТЕОЙЕН УЧПВПДОПЗП РБДЕОЙС. пОП ПДОП Й ФПЦЕ ДМС ЧУЕИ ФЕМ Й ЪБЧЙУЙФ МЙЫШ ПФ ЧЩУПФЩ ОБД ХТПЧОЕН НПТС Й ПФ ЗЕПЗТБЖЙЮЕУЛПК ЫЙТПФЩ. еУМЙ Ч НПНЕОФ ОБЮБМБ ПФУЮЕФБ ЧТЕНЕОЙ (t0 = 0) ФЕМП ЙНЕМП УЛПТПУФШ v0, ФП РП ЙУФЕЮЕОЙЙ РТПЙЪЧПМШОПЗП РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t = t — t0 УЛПТПУФШ ФЕМБ РТЙ УЧПВПДОПН РБДЕОЙЙ ВХДЕФ: v = v0 + g·t. рХФШ h, РТПКДЕООЩК ФЕМПН Ч УЧПВПДОПН РБДЕОЙЙ, Л НПНЕОФХ ЧТЕНЕОЙ t: нПДХМШ УЛПТПУФЙ ФЕМБ РПУМЕ РТПИПЦДЕОЙС Ч УЧПВПДОПН РБДЕОЙЙ РХФЙ h ОБИПДЙФУС ЙЪ ЖПТНХМЩ: рТПДПМЦЙФЕМШОПУФШ ∆t УЧПВПДОПЗП РБДЕОЙС ВЕЪ ОБЮБМШОПК УЛПТПУФЙ (v0 = 0) У ЧЩУПФЩ h: рТЙНЕТ 1. фЕМП РБДБЕФ ЧЕТФЙЛБМШОП ЧОЙЪ У ЧЩУПФЩ 20 Н ВЕЪ ОБЮБМШОПК УЛПТПУФЙ. пРТЕДЕМЙФШ: 1) РХФШ h, РТПКДЕООЩК ФЕМПН ЪБ РПУМЕДОАА УЕЛХОДХ РБДЕОЙС, 2) УТЕДОАА УЛПТПУФШ РБДЕОЙС vУТ, 3) УТЕДОАА УЛПТПУФШ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ vУТ2.	тЕЫЕОЙЕ: оБРТБЧЙН ПУШ Х ЧЕТФЙЛБМШОП ЧОЙЪ, Й РХУФШ ОБЮБМП ЛППТДЙОБФ УПЧРБДБЕФ У ОБЮБМШОЩН РПМПЦЕОЙЕН ФЕМБ (ТЙУХОПЛ 1.5). 1) уПЗМБУОП ЖПТНХМЕ: ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ЪБРЙЫЕФУС Ч ЧЙДЕ: Ч НПНЕОФ РБДЕОЙС ОБ ЪЕНМА Х = h0. пФУАДБ ЧТЕНС ДЧЙЦЕОЙС ФЕМБ: ъБ ЧТЕНС ( t — ∆t) ФЕМП РТПЫМП РХФШ рХФШ ЪБ РПУМЕДОАА УЕЛХОДХ ТБЧЕО: 2) фЕМП РТПЫМП РХФШ h0. чТЕНС ДЧЙЦЕОЙС . фПЗДБ УТЕДОСС УЛПТПУФШ РБДЕОЙС ЙМЙ , 3) дМС ПРТЕДЕМЕОЙС УТЕДОЕК УЛПТПУФЙ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ, ОЕПВИПДЙНП ХЪОБФШ ЧТЕНС, ЪБ ЛПФПТПЕ ЬФБ ЮБУФШ РХФЙ РТПКДЕОБ. чТЕНС ДЧЙЦЕОЙС ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ ТБЧОП РПМОПНХ ЧТЕНЕОЙ РПМЕФБ t НЙОХУ ЧТЕНС t1, ЪБФТБЮЕООПЕ ОБ РТПИПЦДЕОЙЕ РЕТЧПК РПМПЧЙОЩ РХФЙ. чТЕНС t1 ОБИПДЙФУС ЙЪ ХТБЧОЕОЙС:	,Ф.Е.

фБЛЙН ПВТБЪПН,

уМЕДПЧБФЕМШОП,

рТЙ ДЧЙЦЕОЙЙ ФЕМБ ЧЕТФЙЛБМШОП ЧЧЕТИ У ОБЮБМШОПК УЛПТПУФША v₀, ХУЛПТЕОЙЕ ФЕМБ ТБЧОП ХУЛПТЕОЙА УЧПВПДОПЗП РБДЕОЙС g. оБ ХЮБУФЛЕ ДП ОБЙЧЩУЫЕК ФПЮЛЙ РПДЯЕНБ ДЧЙЦЕОЙЕ ФЕМБ СЧМСЕФУС ТБЧОПЪБНЕДМЕООЩН, Б РПУМЕ ДПУФЙЦЕОЙС ЬФПК ФПЮЛЙ — УЧПВПДОЩН РБДЕОЙЕН ВЕЪ ОБЮБМШОПК УЛПТПУФЙ.

уЛПТПУФШ ФЕМБ Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t ПФ ОБЮБМБ ДЧЙЦЕОЙС ОЕЪБЧЙУЙНП ПФ ФПЗП, ТБУУНБФТЙЧБЕФУС МЙЫШ РПДЯЕН ФЕМБ ЙМЙ ЕЗП ПРХУЛБОЙЕ РПУМЕ ДПУФЙЦЕОЙС ОБЙЧЩУЫЕК ФПЮЛЙ, ТБЧОБ v = v₀ + g·t.

чЕЛФПТ РЕТЕНЕЭЕОЙС ∆r ФЕМБ ЪБ РТПЙЪЧПМШОЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t₀, РТЙ ХУМПЧЙЙ t₀ = 0, ТБЧЕО:

ч НПНЕОФ ЧТЕНЕОЙ t_РПД, УППФЧЕФУФЧХАЭЙК ОБЙВПМШЫЕНХ РПДЯЕНХ ФЕМБ ОБД ФПЮЛПК ВТПУБОЙС (ЛПЗДБ Х = Х_НБИ ЙМЙ ЧЩУПФБ РПДЯЕНБ ФЕМБ НБЛУЙНБМШОБ h = h_max = Х_max — Х₀) УЛПТПУФШ ФЕМБ УФБОЕФ ТБЧОБ ОХМА: v = v₀ — g·t_РПД = 0, ПФЛХДБ t_РПД = v₀/g, Ч ЬФПФ НПНЕОФ ОБРТБЧМЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ЙЪНЕОСЕФУС ОБ РТПФЙЧПРПМПЦОПЕ.

нБЛУЙНБМШОБС ЧЩУПФБ РПДЯЕНБ ФЕМБ ОБД ФПЮЛПК ВТПУБОЙС:

1.1.6 дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ Й ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП У ОЕЛПФПТПК ЧЩУПФЩ

дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП У ОЕЛПФПТПК ЧЩУПФЩ, НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ ОЕЪБЧЙУЙНЩИ ДЧЙЦЕОЙС: ТБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ, РТПЙУИПДСЭЕЕ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ УП УЛПТПУФША υ_И , ТБЧОПК ОБЮБМШОПК УЛПТПУФЙ ВТПУБОЙС υ₀ (υ_И = υ₀), Й УЧПВПДОПЕ РБДЕОЙЕ У ЧЩУПФЩ, ОБ ЛПФПТПК ОБИПДЙМПУШ ФЕМП Ч НПНЕОФ ВТПУБОЙС, У ХУЛПТЕОЙЕН g. дМС ПРЙУБОЙС ЬФПЗП ДЧЙЦЕОЙС ЧЩВЙТБАФ РТСНПХЗПМШОХА УЙУФЕНХ ЛППТДЙОБФ ИпХ. фТБЕЛФПТЙС ДЧЙЦЕОЙС СЧМСЕФУС ЧЕФЧШ РБТБВПМЩ (ТЙУХОПЛ 1.6).

хТБЧОЕОЙЕ ДЧЙЦЕОЙС РП ПУСН пИ Й пХ:

уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ НПЦОП ПРТЕДЕМЙФШ РП ЖПТНХМЕ:

рТЙ ЬФПН ЧТЕНС РПМЕФБ УЧСЪБОП У ЧЕТФЙЛБМШОПК УПУФБЧМСАЭЕК ДЧЙЦЕОЙС. дБМШОПУФШ РПМЕФБ — У ЗПТЙЪПОФБМШОПК.

рТЙНЕТ 1. у ВБЫОЙ ЧЩУПФПК о = 25 Н ЗПТЙЪПОФБМШОП ВТПЫЕО ЛБНЕОШ УП УЛПТПУФША υ₀ = 15 Н/У. оБКФЙ: УЛПМШЛП ЧТЕНЕОЙ ЛБНЕОШ ВХДЕФ Ч ДЧЙЦЕОЙЙ; ОБ ЛБЛПН ТБУУФПСОЙЙ S_x ПФ ПУОПЧБОЙЙ ВБЫОЙ ПО ХРБДЕФ ОБ ЪЕНМА; У ЛБЛПК УЛПТПУФША υ ПО ХРБДЕФ ОБ ЪЕНМА; ЛБЛПК ХЗПМ φ УПУФБЧЙФ ФТБЕЛФПТЙС ЛБНОС У ЗПТЙЪПОФПН Ч ФПЮЛЕ ЕЗП РБДЕОЙС ОБ ЪЕНМА.

рЕТЕНЕЭЕОЙЕ ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП ЛБНОС НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ (ТЙУХОПЛ 1.7): ЗПТЙЪПОФБМШОПЕ S_x Й ЧЕТФЙЛБМШОПЕ S_y.

рТЙНЕОСС ЪБЛПО ОЕЪБЧЙУЙНПУФЙ ДЧЙЦЕОЙС, ЙНЕЕН:

, , ПФУАДБ,

1)

2) S_x = L = v₀·t = 15 · 2,26 = 33,9 Н;

3) v_Х = g · t = 9,81 · 2,26 = 22,1 Н/У,

4)

дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ, ФБЛЦЕ НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ ОЕЪБЧЙУЙНЩИ ДЧЙЦЕОЙС: ТБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ, РТПЙУИПДСЭЕЕ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ У ОБЮБМШОПК УЛПТПУФША v_0И = v₀·Cosα Й УЧПВПДОПЕ РБДЕОЙЕ У ОБЮБМШОПК УЛПТПУФША v_0Х = v₀·Sinα, (ТЙУХОПЛ 1.8). зДЕ α — ХЗПМ НЕЦДХ ОБРТБЧМЕОЙСНЙ ЧЕЛФПТБ УЛПТПУФЙ υ₀ Й ПУША пИ. фТБЕЛФПТЙЕК ФБЛПЗП ДЧЙЦЕОЙС СЧМСЕФУС РБТБВПМБ. хТБЧОЕОЙС ДЧЙЦЕОЙС РТЙНХФ ЧЙД:

уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ:

рТЙНЕТ 2. фЕМП ВТПЫЕОП РПД ХЗМПН α Л ЗПТЙЪПОФХ У ОБЮБМШОПК УЛПТПУФША υ₀. пРТЕДЕМЙФШ ЧТЕНС РПМЕФБ t, НБЛУЙНБМШОХА ЧЩУПФХ о РПДЯЕНБ Й ДБМШОПУФШ L РПМЕФБ.

тЕЫЕОЙЕ: лБЛ ПВЩЮОП ЪБДБЮБ ОБЮЙОБЕФУС У ЧЩСЧМЕОЙС УЙМ, ДЕКУФЧХАЭЙИ ОБ ФЕМП. оБ ФЕМП ДЕКУФЧХЕФ ФПМШЛП УЙМБ ФСЦЕУФЙ, РПЬФПНХ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ ПОП РЕТЕНЕЭБЕФУС ТБЧОПНЕТОП, Б Ч ЧЕТФЙЛБМШОПН — ТБЧОПРЕТЕНЕООП У ХУЛПТЕОЙЕН g.

вХДЕН ТБУУНБФТЙЧБФШ ЧЕТФЙЛБМШОХА Й ЗПТЙЪПОФБМШОХА УПУФБЧМСАЭЙЕ ДЧЙЦЕОЙС ФЕМБ РП ПФДЕМШОПУФЙ, ДМС ЬФПЗП ТБЪМПЦЙН ЧЕЛФПТ ОБЮБМШОПК УЛПТПУФЙ ОБ ЧЕТФЙЛБМШОХА ( υ₀·Sinα ) Й ЗПТЙЪПОФБМШОХА ( υ₀·Cosα ) УПУФБЧМСАЭЙЕ (ТЙУХОПЛ 1.9).

оБЮОЕН ТБУУНБФТЙЧБФШ ЧЕТФЙЛБМШОХА УПУФБЧМСАЭХА ДЧЙЦЕОЙС. чТЕНС РПМЕФБ t = t₁ + t₂, ЗДЕ t₁ — ЧТЕНС РПДЯЕНБ (ФЕМП ДЧЙЦЕФУС РП ЧЕТФЙЛБМЙ ТБЧОПЪБНЕДМЕООП), t₂ — ЧТЕНС УРХУЛБ (ФЕМП ДЧЙЦЕФУС РП ЧЕТФЙЛБМЙ ТБЧОПХУЛПТЕООП).

чЕТФЙЛБМШОБС УЛПТПУФШ ФЕМБ Ч ОБЙЧЩУЫЕК ФПЮЛЕ ФТБЕЛФПТЙЙ (РТЙ t = t₁) ТБЧОБ ПЮЕЧЙДОП ОХМА. у ДТХЗПК УФПТПОЩ, ЬФБ УЛПТПУФШ НПЦЕФ ВЩФШ ЧЩТБЦЕОБ РТЙ РПНПЭЙ ЖПТНХМЩ ЪБЧЙУЙНПУФЙ УЛПТПУФЙ ТБЧОПЪБНЕДМЕООПЗП ДЧЙЦЕОЙС ПФ ЧТЕНЕОЙ.

пФУАДБ, РПМХЮБЕН: 0 = υ₀Sinα — g·t₁ ЙМЙ

(1.2)

рПДУФБЧЙН (1.1) Ч (1.2)

чТЕНС УРХУЛБ t₂ НПЦОП ЧЩЮЙУМЙФШ, ТБУУНПФТЕЧ РБДЕОЙЕ ФЕМБ У ЙЪЧЕУФОПК ЧЩУПФЩ о ВЕЪ ОБЮБМШОПК ЧЕТФЙЛБМШОПК УЛПТПУФЙ:

рПМОПЕ ЧТЕНС РПМЕФБ:

дМС ОБИПЦДЕОЙС ДБМШОПУФЙ РПМЕФБ L ОЕПВИПДЙНП ПВТБФЙФШУС Л ЗПТЙЪПОФБМШОПК УПУФБЧМСАЭЕК ДЧЙЦЕОЙС ФЕМБ. лБЛ ХЦЕ ПФНЕЮБМПУШ, РП ЗПТЙЪПОФБМЙ ФЕМП РЕТЕНЕЭБЕФУС ТБЧОПНЕТОП.

1.1.7 тБЧОПРЕТЕНЕООПЕ ДЧЙЦЕОЙЕ ФПЮЛЙ РП ПЛТХЦОПУФЙ

дЧЙЦЕОЙЕ РП ПЛТХЦОПУФЙ СЧМСЕФУС РТПУФЕКЫЙН РТЙНЕТПН ЛТЙЧПМЙОЕКОПЗП ДЧЙЦЕОЙС. уЛПТПУФШ υ ДЧЙЦЕОЙС РП ПЛТХЦОПУФЙ ОБЪЩЧБЕФУС МЙОЕКОПК (ПЛТХЦОПК) УЛПТПУФША. рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ РП ПЛТХЦОПУФЙ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ У ФЕЮЕОЙЕН ЧТЕНЕОЙ ОЕ ЙЪНЕОСЕФУС. дЧЙЦХЭБСУС ФПЮЛБ ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ РТПИПДЙФ ТБЧОЩЕ РП ДМЙОЕ ДХЗЙ ПЛТХЦОПУФЙ. фБОЗЕОГЙБМШОПЕ ХУЛПТЕОЙЕ РТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ПФУХФУФЧХЕФ ( a_τ ). йЪНЕОЕОЙЕ ЧЕЛФПТБ УЛПТПУФЙ υ РП ОБРТБЧМЕОЙА ИБТБЛФЕТЙЪХЕФУС ОПТНБМШОЩН ХУЛПТЕОЙЕН a_n, ЛПФПТПЕ ОБЪЩЧБЕФУС ФБЛЦЕ ГЕОФТПУФТЕНЙФЕМШОЩН ХУЛПТЕОЙЕН.

ч ЛБЦДПК ФПЮЛЕ ФТБЕЛФПТЙЙ ЧЕЛФПТ a_n ОБРТБЧМЕО РП ТБДЙХУХ Л ГЕОФТХ ПЛТХЦОПУФЙ, Б ЕЗП НПДХМШ ТБЧЕО:

рТЙ ПРЙУБОЙЙ НЕИБОЙЮЕУЛПЗП ДЧЙЦЕОЙС, Ч ЮБУФОПУФЙ ДЧЙЦЕОЙС РП ПЛТХЦОПУФЙ, ОБТСДХ У РТСНПХЗПМШОПК ДЕЛБТФПЧПК УЙУФЕНПК ЛППТДЙОБФ ЙУРПМШЪХЕФУС РПМСТОБС УЙУФЕНБ ЛППТДЙОБФ. рПМПЦЕОЙЕ ФПЮЛЙ н ОБ ЛБЛПК-ФП РМПУЛПУФЙ (ОБРТЙНЕТ, ипх) ПРТЕДЕМСЕФУС ДЧХНС РПМСТОЩНЙ ЛППТДЙОБФБНЙ: НПДХМЕН r ТБДЙХУБ ЧЕЛФПТБ ФПЮЛЙ Й ХЗМПН φ — ХЗМПЧПК ЛППТДЙОБФПК, ЙМЙ РПМСТОЩН ХЗМПН (ТЙУХОПЛ 1.10).

хЗПМ φ ПФУЮЙФЩЧБЕФУС ПФ ПУЙ пи ДП ТБДЙХУБ-ЧЕЛФПТБ r РТПФЙЧ ЮБУПЧПК УФТЕМЛЙ. фПЮЛХ п Ч ЬФПН УМХЮБЕ ОБЪЩЧБАФ РПМАУПН УЙУФЕНЩ ЛППТДЙОБФ. уПЧНЕУФЙН РПМАУ ЛППТДЙОБФ УЙУФЕНЩ У ГЕОФТПН ПЛТХЦОПУФЙ, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ; ФПЗДБ r = R (ТЙУХОПЛ 1.11), Б ЙЪНЕОЕОЙЕ РПМПЦЕОЙС ФПЮЛЙ ОБ ПЛТХЦОПУФЙ НПЦЕФ ВЩФШ ПИБТБЛФЕТЙЪПЧБОП ЙЪНЕОЕОЙЕН ∆φ ХЗМПЧПК ЛППТДЙОБФЩ ФПЮЛЙ: ∆φ = φ₂ -φ₁.

хЗПМ ∆φ ОБЪЩЧБЕФУС ХЗМПН РПЧПТПФБ ТБДЙХУБ — ЧЕЛФПТБ ФПЮЛЙ. ьМЕНЕОФБТОЩЕ (ВЕУЛПОЕЮОП НБМЩЕ) ХЗМЩ РПЧПТПФБ ТБУУНБФТЙЧБАФУС ЛБЛ ЧЕЛФПТЩ.

нПДХМШ ЧЕЛФПТБ dφ ТБЧЕО ХЗМХ РПЧПТПФБ. оБРТБЧМЕОЙЕ ЧЕЛФПТБ dφ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС ПУФТЙС ЧЙОФБ, ЗПМПЧЛБ ЛПФПТПЗП, ЧТБЭБЕФУС Ч ОБРТБЧМЕОЙЙ ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ, Ф.Е. РПДЮЙОСЕФУС РТБЧЙМХ РТБЧПЗП ЧЙОФБ (ТЙУХОПЛ 1.12).

CТЕДОЕК ХЗМПЧПК УЛПТПУФША ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ ЧПЛТХЗ ПУЙ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ ω_cp, ТБЧОБС ПФОПЫЕОЙА ХЗМБ РПЧПТПФБ ∆φ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ДМЙФЕМШОПУФЙ ЬФПЗП РТПНЕЦХФЛБ:

хЗМПЧПК УЛПТПУФША (НЗОПЧЕООПК ХЗМПЧПК УЛПТПУФША) ω ОБЪЩЧБЕФУС РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС ХЗМПЧБС УЛПТПУФШ РТЙ ВЕУЛПОЕЮОПН ХНЕОШЫЕОЙЙ РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t, ЙМЙ РЕТЧБС РТПЙЪЧПДОБС ПФ ХЗМБ РПЧПТПФБ РП ЧТЕНЕОЙ:

чЕЛФПТ ω ОБРТБЧМЕО ЧДПМШ ПУЙ ЧТБЭЕОЙС РП РТБЧЙМХ РТБЧПЗП ЧЙОФБ, Ф.Е. ФБЛЦЕ ЛБЛ Й dφ (ТЙУХОПЛ 1.13).

рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ХЗМЩ РПЧПТПФБ ЕЕ ТБДЙХУ-ЧЕЛФПТБ ПДЙОБЛПЧЩ. уМЕДПЧБФЕМШОП, РТЙ ФБЛПН ДЧЙЦЕОЙЙ НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ: ω = ω_cp. хЗПМ РПЧПТПФБ ∆ω ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ, ТБЧОПНЕТОП ДЧЙЦХЭЕКУС РП ПЛТХЦОПУФЙ, ТБЧЕО:

рТПНЕЦХФПЛ ЧТЕНЕОЙ ф, Ч ФЕЮЕОЙЙ ЛПФПТПЗП ФПЮЛБ УПЧЕТЫБЕФ ПДЙО РПМОЩК ПВПТПФ РП ПЛТХЦОПУФЙ, ОБЪЩЧБЕФУС РЕТЙПДПН ПВТБЭЕОЙС (РЕТЙПДПН ЧТБЭЕОЙС), Б ЧЕМЙЮЙОБ υ, ПВТБФОБС РЕТЙПДХ:

,

ЮБУФПФПК ПВТБЭЕОЙС (ЮБУФПФПК ЧТБЭЕОЙС). ъБ ПДЙО РЕТЙПД ХЗПМ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ТБЧЕО 2π ТБД, РПЬФПНХ 2π = ωT, ПФЛХДБ T = 2π/ω, ЙМЙ ω = 2π/ф = 2πν.

мЙОЕКОБС υ Й ХЗМПЧБС ω УЛПТПУФЙ УЧСЪБОЩ УППФОПЫЕОЙЕН: υ = ω·R. ьФП ЧЙДОП ЙЪ УМЕДХАЭЕЗП ЧЩЧПДБ:

рТЙНЕТ 1. пРТЕДЕМЙФШ НПДХМШ УЛПТПУФЙ Й ГЕОФТПУФТЕНЙФЕМШОПЗП ХУЛПТЕОЙС ФПЮЕЛ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ. тБДЙХУ ъЕНМЙ РТЙОСФШ ТБЧОЩН 6400 ЛН.

R = 6400 ЛН = 6,4·10 6 Н;

ф = 24 Ю = 8,64·10 4 У;

тЕЫЕОЙЕ: фПЮЛЙ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ ДЧЙЦХФУС РП ПЛТХЦОПУФЙ ТБДЙХУБ R, РПЬФПНХ НПДХМШ ЙИ УЛПТПУФЙ:

пФЧЕФ: υ = 465 Н/У, Б_ГУ = 0,034 Н /У 2 .

1.1.8 чТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ

дМС ЛЙОЕНБФЙЮЕУЛПЗП ПРЙУБОЙС ЧТБЭБФЕМШОПЗП ДЧЙЦЕОЙС БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ЛБЛПК-ФП ОЕРПДЧЙЦОПК ПУЙ ЙУРПМШЪХАФУС ФЕ ЦЕ ЧЕМЙЮЙОЩ (Й ХТБЧОЕОЙС УЧСЪЙ НЕЦДХ ОЙНЙ), ЮФП Й ДМС ПРЙУБОЙС ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ. рТЙ ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t ХЗМЩ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТПЧ ТБЪМЙЮОЩИ ФПЮЕЛ ФЕМБ ПДЙОБЛПЧЩ. хЗПМ РПЧПТПФБ ∆φ, УТЕДОСС ω_cp Й НЗОПЧЕООБС ω ХЗМПЧЩЕ УЛПТПУФЙ ИБТБЛФЕТЙЪХАФ ЧТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ ЧУЕЗП БВУПМАФОП ФЧЕТДПЗП ФЕМБ Ч ГЕМПН.

мЙОЕКОБС УЛПТПУФШ υ ЛБЛПК-МЙВП ФПЮЛЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ РТПРПТГЙПОБМШОП ТБУУФПСОЙА R ФПЮЛЙ ПФ ПУЙ ЧТБЭЕОЙС:

рТЙ ТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ПДЙОБЛПЧЩ ( ∆φ = const ) Й НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ФЕМБ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ ( ω = ω_cp ). фБОЗЕОГЙБМШОЩЕ ХУЛПТЕОЙС a_τ Х ТБЪМЙЮОЩИ ФПЮЕЛ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ПФУХФУФЧХАФ ( a_τ = 0 ), Б ОПТНБМШОПЕ (ГЕОФТПУФТЕНЙФЕМШОПЕ ) ХУЛПТЕОЙЕ a_n ЛБЛПК-МЙВП ФПЮЛЙ ФЕМБ ЪБЧЙУЙФ ПФ ЕЕ ТБУУФПСОЙС R ДП ПУЙ ЧТБЭЕОЙС:

чЕЛФПТ a_n ОБРТБЧМЕО Ч ЛБЦДЩК НПНЕОФ ЧТЕНЕОЙ РП ТБДЙХУХ ФТБЕЛФПТЙЙ ФПЮЛЙ Л ПУЙ ЧТБЭЕОЙС.

рТЙ ОЕТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ОЕПДЙОБЛПЧЩ. хЗМПЧБС УЛПТПУФШ ФЕМБ ω У ФЕЮЕОЙЕН ЧТЕНЕОЙ ЙЪНЕОСЕФУС.

уТЕДОЙН ХЗМПЧЩН ХУЛПТЕОЙЕН ε_УТ Ч РТПНЕЦХФЛЕ ЧТЕНЕОЙ ∆t = t₂ — t₁ ОБЪЩЧБЕФУС ЖЙЪЙЮЕУЛБС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА ЙЪНЕОЕОЙС ХЗМПЧПК УЛПТПУФЙ ∆ω = ω₂ — ω₁ ЧТБЭБАЭЕЗПУС ФЕМБ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ДМЙФЕМШОПУФЙ ЬФПЗП РТПНЕЦХФЛБ:

еУМЙ ХЗМПЧБС УЛПТПУФШ ЪБ РТПЙЪЧПМШОЩЕ ПДЙОБЛПЧЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ЙЪНЕОСЕФУС ПДЙОБЛПЧП ( ∆ω₁₂ = ∆ω₃₄ Й Ф.Д.), ФП ε_УТ = const (ТБЧОПРЕТЕНЕООПЕ ЧТБЭЕОЙЕ).

хЗМПЧЩН ХУЛПТЕОЙЕН (НЗОПЧЕООЩН ХЗМПЧЩН ХУЛПТЕОЙЕН) ЧТБЭБАЭЕЗПУС ФЕМБ Ч НПНЕОФ ЧТЕНЕОЙ t ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ ε, ТБЧОБС РТЕДЕМХ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОЕЕ ХЗМПЧПЕ ХУЛПТЕОЙЕ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ПФ t ДП t + ∆t РТЙ ВЕУЛПОЕЮОПН ХНЕОШЫЕОЙЙ ∆t, ЙМЙ, ХЗМПЧПЕ ХУЛПТЕОЙЕ — ЬФП РЕТЧБС РТПЙЪЧПДОБС ПФ ХЗМПЧПК УЛПТПУФЙ РП ЧТЕНЕОЙ ЙМЙ ЧФПТБС РТПЙЪЧПДОБС ПФ ХЗМБ РПЧПТПФБ РП ЧТЕНЕОЙ:

йЪНЕОЕОЙЕ ∆ω ХЗМПЧПК УЛПТПУФЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t₀ РТЙ ТБЧОПРЕТЕНЕООПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ У ХЗМПЧЩН ХУЛПТЕОЙЕН ε: ∆ω = ε·∆t = ε(t — t₀). еУМЙ РТЙ t₀ = 0 ОБЮБМШОБС ХЗМПЧБС УЛПТПУФШ ФЕМБ ТБЧОБ ω₀, ФП Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t ХЗМПЧБС УЛПТПУФШ ФЕМБ ВХДЕФ ω = ω₀ + ε·t.

хЗПМ РПЧПТПФБ ∆φ ФЕМБ ЧПЛТХЗ ПУЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t₀ РТЙ ТБЧОПРЕТЕНЕООПН ДЧЙЦЕОЙЙ:

фБОЗЕОГЙБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:

; υ = ω·R, РПЬФПНХ

оПТНБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:

фБЛЙН ПВТБЪПН, УЧСЪШ НЕЦДХ МЙОЕКОЩНЙ Й ХЗМПЧЩНЙ ЧЕМЙЮЙОБНЙ ЧЩТБЦБЕФУС УМЕДХАЭЙНЙ ЖПТНХМБНЙ: S = R·φ, υ = ω·R, a_τ = R·ε, a_n = ω 2 ·R.

Прямолинейное равномерное движение

Содержание:

Равномерным прямолинейным движением называется такое прямолинейное движение, при котором материальная точка (тело) движется по прямой и в любые равные промежутки времени совершает одинаковые перемещения.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Прямолинейное равномерное движение

Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения. Скорость равномерного прямолинейного движения точки – величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.

Механическое движение

Вдали на дороге виден автомобиль. Мы не слышим шума его мотора и не видим, вращаются его колёса или нет. Как определить—движется автомобиль по дороге или нет?

Проследим за положением автомобиля относительно каких-либо неподвижных предметов, находящихся у дороги, например телеграфных столбов или деревьев. Если расстояние автомобиля от этих неподвижных предметов меняется, мы заключаем, что автомобиль движется; если же не меняется, значит автомобиль находится в покое.

Подобным же образом мы определяем, движется или нет поезд, пароход, самолёт—вообще любое тело.

Изменение положения данного тела относительно других тел называется механическим движением.

Механические движения тел весьма разнообразны. Движение планет, облаков, воды в реках и океанах, поездов, самолётов, автомобилей, различных частей машин и станков, людей, животных, полёт птиц—всё это лишь немногие примеры механических движений.

Все тела природы, все частицы, из которых состоят эти тела, находятся в движении. На первый взгляд кажется, что это не всегда верно; например, дома стоят неподвижно, неподвижны горы, леса и многие другие предметы. В действительности же все эти предметы неподвижны только относительно друг друга, но они вместе с Землёй совершают суточное вращение и движутся вокруг Солнца.

В природе не существует совершенно неподвижного тела.

Механическое движение совершают все тела природы и частицы, из которых состоят эти тела.

Механические движения изучаются в разделе физики, называемом механикой. Слово механика произошло от греческого слова „механэ“, что значит машина или приспособление.

Машины ещё в глубокой древности применялись в транспорте, а также в строительном и военном деле. На рисунке 2 изображено применение древними египтянами рычагов при постройке пирамид.

Рис. 2. Применение рычагов при постройке пирамид в древнем Египте.

Законы механики лежат в основе устройства и сложнейших современных машин. На рисунке 3 изображён современный башенный подъёмный кран, применяющийся на наших стройках. Один такой кран выполняет работу тысячи рабочих.

Относительность движения и покоя

Движением, как мы видели, называется изменение положения данного тела относительно каких-либо других тел. Пароход, например, движется относительно берега, поезд—относительно полотна железной дороги, резец токарного станка—относительно основания станка и т. д. Но и берег, и полотно железной дороги, и основание станка сами находятся в движении вместе с Землёй; мы лишь условно принимаем их за неподвижные тела.

Движение тела относительно других тел, условно принимаемых за неподвижные, называется относительным движением.

Так как все тела природы находятся в движении и абсолютно (Абсолют—от латинского слова абсолютус—безусловный) неподвижных тел нет, то не существует и абсолютных движений, точно так же как не существует и абсолютного покоя.

Всякое движение, так же как и всякий покой, является относительным.

Одно и то же движение, рассматриваемое относительно разных тел, будет представляться по-разному. Представим себе пассажира, сидящего в вагоне движущегося поезда. Что можно сказать о его движении? Проводник вагона скажет о пассажире, что он неподвижен (сидит), стрелочник, мимо которого движется поезд, уверяет, что пассажир движется мимо него. И в сущности каждый из них прав. Проводник вагона, заявляя о том, что пассажир не движется, рассматривает положение пассажира относительно предметов в вагоне. Стрелочник, стоящий на земле и наблюдающий за движением поезда, рассматривает положение пассажира или относительно полотна дороги, или относительно себя.

Так как два наблюдателя рассматривали положение пассажира относительно разных предметов,то они и пришли к различным выводам.

Рассмотрим другой пример. Пассажир находится в закрытой каюте речного парохода, где он видит только стены каюты и закрытое занавеской окно. Может ли он сказать что-либо определённое о движении парохода? При спокойном ходе парохода, не слыша шума работы машины, невозможно определить, движется пароход или нет. Надо открыть окно, найти какой-либо неподвижный предмет на берегу и только по изменению расстояния от этого предмета можно будет судить о движении парохода.

Рис. 3. Башенный кран, применяющийся на стройках.

Таким образом, желая определить, движется тело или нет
и как оно движется, мы должны указать, относительно каких тел рассматривается интересующее нас движение.

Тела, относительно которых рассматривается движение, называются телами отсчёта.

В дальнейшем при изучении различных движений в качестве тела отсчёта мы будем брать Землю или какое-либо другое тело, неподвижное относительно Земли, например стол физического кабинета, где производятся опыты.

Вопрос об относительности движения и покоя изучался знаменитым итальянским учёным Галилео Галилеем. Ниже приводится выписка из его книги, впервые опубликованной в 1632 г., в которой он излагает свои взгляды по данному вопросу.

Движение твёрдого тела и движение точки

Механические движения тел в природе и технике могут быть весьма разнообразны и сложны.

Наиболее простым видом движения тела является поступательное движение. При поступательном движении любая прямая, проведённая в теле, остаётся параллельной самой себе.

Поступательным движением является, например, движение ящика, выдвигаемого из стола, движение поршня в цилиндре паровой машины или в двигателе внутреннего сгорания, движение вагона на прямолинейном участке железнодорожного пути, движение резца вдоль корпуса токарного станка (рис. 4) или детали на продольно-строгальном станке относительно резца (рис. 5). На рисунке 6 показано поступательное движение карандаша.

Рис. 4. Поступательное движение резца токарного станка.

Рис. 5. Поступательное движение детали на продольно-строгальном станке.

Рис. 6. Поступательное движение карандаша.

При поступательном движении все точки тела проходят одинаковые расстояния и при своём движении описывают одинаковые линии. Поэтому, чтобы изучать поступательное движение твёрдого тела, достаточно изучить движение какой — нибудь одной точки тела.

В дальнейшем мы часто будем говорить о движении тела, рассматривая его как точку.

Если непрерывно отмечать положение движущегося тела в пространстве точками, например: и т. д. (рис. 7), то получится линия, называемая траекторией движения. Проводя карандашом по бумаге, мы оставляем на ней след—траекторию движения кончика карандаша. Стрельба трассирующими пулями по цели облегчает пристрелку, так как видна траектория движения пули. Попав в атмосферу Земли и раскалившись, метеорит оставляет на короткое время светящийся след, указывающий траекторию его полёта.

Рис. 7. Траектория движущейся точки.

Отсчёт пройденного пути за заданный промежуток времени производится вдоль траектории от некоторой условно выбранной на траектории точки, например от (рис. 7), в которой в момент начала наблюдений находится тело.

Во всяком движении длина пути, пройденного точкой, зависит от времени. Найти способы определять положение точки на траектории в любой момент времени—значит установить закон движения точки.

Закон движения может быть выражен различно: его можно представить в виде математической формулы, связывающей величины, характеризующие движение; можно представить в виде таблицы и, наконец, можно изобразить графически в виде некоторой линии.

Движение точки является определённым, если установлена траектория и известен закон движения её по этой траектории.

Различные виды движения тела

Траектория движения тела может быть прямолинейной и криволинейной. Соответственно этому движения тела разделяются на прямолинейные и криволинейные.

Рис. 9. Примеры криволинейных движений.

На рисунке 9 изображены простейшие примеры криволинейного движения: движение концов стрелок часов и движение мячика, брошенного под углом к горизонту.

Независимо от формы траектории движения разделяются на равномерные и неравномерные.

Равномерным называется такое движение, при котором в любые равные промежутки времени тело проходит одинаковые пути.

Так, например, если тело в первую секунду от начала наблюдения за его движением проходит 10 м, в каждую следующую— также по 10 м, в каждую половину секунды—5 м, в каждую пятую долю секунды—2 ж и т. д., то оно движется равномерно.

Примером равномерного движения, наблюдаемого в природе, может служить движение точки земной поверхности при суточном вращении. За равномерное движение можно принимать движение точек часовой стрелки, движение конвейерной ленты на производстве, движение поезда на длинном и ровном перегоне (равномерность этого движения легко установить, прислушиваясь к стукам при ударе колёс о стыки рельсов) и многие другие.

Рис. 10. Равномерное движение тележки с капельницей.

Установим на тележке капельницу (рис. 10) и при помощи груза уравновесим трение колёс тележки о доску. Затем слегка толкнём тележку. Вытекающие из капельницы капли окрашенной жидкости через равные промежутки времени отметят на бумаге пути, пройденные тележкой. Приблизительно эти пути одинаковы; следовательно, движение тележки с капельницей можно принимать за равномерное движение.

При изучении движения приходится измерять пройденные пути и промежутки времени. Всякие же измерения могут быть произведены только с некоторой степенью точности. Поэтому и равномерность того или иного движения может быть установлена на опыте только с той степенью точности, с которой
производятся измерения.

Скорость движения. Единицы скорости

Мы часто говорим, что одни тела движутся быстрее, другие медленнее. Самолёт, например, движется быстрее автомобиля, а автомобиль может двигаться быстрее самой резвой лошади. Словами „быстро“ и „медленно“ в обыденной речи характеризуют различие в движении тел. В физике величиной, характеризующей различие в быстроте движения тел, является скорость.

В случае равномерного движения о величине скорости мы можем судить по величине пути, который проходит тело за равные промежутки времени. Чем больший путь пройден телом за одно и то же время, тем больше его скорость, и наоборот. Поэтому величина скорости в равномерном движении характеризуется путём, пройденным телом в единицу времени. Следовательно, для нахождения скорости движения надо измерить две величины: путь и время, за которое пройден этот путь. Тогда частное от деления пути на время даст нам величину скорости.

Обозначим скорость буквой v. Если за время t пройден путь s, то скорость:

Скоростью равномерного движения называется величина, измеряемая отношением пути ко времени, за которое этот путь пройден.

Положив в написанной выше формуле s = 1 ед. пути, t = 1 ед. времени, получим ед. скорости.

Это значит, что единицей, скорости является скорость такого движения, при котором за единицу времени тело проходит единицу пути.

Если измерять путь в сантиметрах, а время в секундах, то единицей скорости будет скорость такого движения, при котором тело за 1 сек. проходит 1 см. Наименование такой единицы скорости: Единицами скорости могут быть также: и др.

Положим, что поезд, двигаясь с неизменной скоростью, за 2 часа прошёл путь 72 км. Вычислим скорость движения поезда: s = 72 км; t = 2 часа;

В данном случае единицей скорости является

Найдём численное значение полученной скорости, приняв за единицу скорости

Если же за единицу скорости принять то получим следующее численное значение скорости:

Таким образом, численное значение величины скорости зависит от выбранной нами единицы скорости, или, что то же, от численных значений пути и времени.

При поступательном движении тела все его точки движутся с одной и той же скоростью. Поэтому скорость какой-либо точки тела одновременно будет скоростью всего тела.

Ниже в таблице приведены скорости некоторых движений, наблюдаемых в природе и в современной технике.

Графическое изображение движения

В технике скорость движения определяется с помощью специальных приборов. Один из таких приборов, называемый спидометром, устанавливается на автомобиле (рис. 11). Механизм спидометра соединён с колёсами автомобиля. Скорость движения автомобиля отмечается стрелкой на шкале спидометра.

Рис. 11. Спидометр на автомобиле (справа дан в большем масштабе).

Когда автомобиль движется с переменной скоростью,то стрелка спидометра указывает то на одну, то на другую цифру на шкале; когда же автомобиль движется некоторое время не меняя скорости, стрелка стоит на одном месте шкалы. Спидометр, таким образом, показывает ту скорость, с которой движется автомобиль в каждый данный момент времени.

Чтобы знать о всех изменениях скорости, которые были при движении автомобиля, для этого пришлось бы составить запись скоростей автомобиля в различные моменты времени. Такую запись можно производить автоматически при помощи специального прибора.

Автоматическая запись производится на специально разграфлённой бумаге, которая при помощи часового механизма относительно,пера на ней вычерчивается график движения.
равномерно движется под пишущим пером. Перо с помощью особого приспособления связано с указателем прибора скорости. Когда указатель неподвижен, то перо тоже неподвижно и чертит на движущейся бумаге прямую линию (рис. 12).

Рис. 12. При движении бумаги относительно пера на ней вычерчивается график движения.

Когда же указатель прибора поднимается или опускается, показывая увеличение или уменьшение скорости, то и перо поднимается или опускается, прочерчивая линию на бумаге. Таким образом, перо отмечает на бумаге все изменения скорости.

Если на клетчатой бумаге отметить величины скоростей, (Соответствующие показаниям прибора, то по нашей записи можно будет определить и величину скорости в любой
момент времени.

На рисунке 13 изображена одна из таких записей. На этой записи можно прочитать, что вся поездка длилась 1 час 5 мин. (бумага передвигается на одну клетку за 5 мин.).В первые 5 мин. автомобиль развил скорость в (одно деление по вертикали соответствует скорости ), затем 15 мин. двигался со скоростью К концу 25-й минуты скорость упала до с этой скоростью автомобиль двигался 10 минут, затем скорость начала падать, и автомобиль остановился на 10 мин.
Рис. 13. Пример графика скорости.

После остановки автомобиль за 5 мин. развил скорость до а затем через 10 мин. снова остановился.

Можно автоматически записывать не только скорости движения автомобиля, но и пройденные им пути.

Рис. 14. Пример графика пути.

На рисунке 14 приведена одна из таких записей. По этой записи видно,что через 20 мин. от начала движения автомобиль прошёл 10 км. За следующие 30 мин. автомобиль прошёл 20 км, затем 5 мин. стоял на месте и последние 15 км прошёл за 10 мин.

Такие записи движения, или, как их называют, графики движения, дают наглядное представление об изучаемом движении.

Уравнение равномерного движения

Было установлено, что при равномерном движении пути, проходимые в равные промежутки времени, одинаковы; поэтому при увеличении промежутка времени в несколько раз во столько же раз увеличивается и путь. Так, если за t сек. пройден путь s см, то за 2 t сек. путь будет 2 s см, за 3 t сек.—3 s см и т. д. Скорость v на этих участках пути выразится так:

А это значит, что скорость при равномерном движении одна и та же на всех участках пути.

Итак, можно сказать, что равномерное движение есть движение с постоянной скоростью.

Зная скорость равномерного движения, можно найти путь, пройденный за время t, по формуле:

Написанная формула называется уравнением равномерного движения. Это уравнение математически выражает зависимость пройденного пути от времени: пройденный путь при равномерном движении прямо пропорционален времени.

П р и м е р. Самолёт летит со скоростью Какое расстояние пройдёт самолёт за 1 мин.?

Решая эту задачу по формуле s = vt, мы должны предварительно либо скорость выразить в либо время в часах.

Очевидно, последнее сделать проще, так как 1 мин.=часа; тогда

При решении подобных задач необходимо, чтобы все величины были выражены в надлежащих единицах.

График пути равномерного движения

Зависимость пути от времени при равномерном движении может быть выражена не только алгебраически, в виде формулы, но и чертежом — графически.

Рис. 15. Оси координат (ось времён и ось пройденных путей).

Рис. 16. Построение графика пути равномерного движения.

Проведём две взаимно перпендикулярные линии Ot и OS. Эти линии будем называть осями координат (рис. 15), ось Ot — осью времён, а ось OS—осью пройденных путей. Точка О пересечения осей обозначает начало отсчётов и для времени и для пути. Отложим в определённом масштабе как на оси Ot, так и на оси OS равные отрезки. Возьмём где-нибудь на нашем чертеже точку А. Опустим из этой точки перпендикуляры на обе оси. Тогда на оси времён получим отрезок ON, численно равный промежутку времени, а на оси путей — отрезок ОМ, соответствующий пройденному пути. Но ОN = AM, где АМ есть расстояние от точки А до оси пройденных путей, а ОМ = AN — расстояние от точки А до оси времен.

Итак, расстояние, измеряемое от какой-либо точки доноси путей, на чертеже соответствует некоторому промежутку времени, а расстояние от этой точки до оси времён — некоторому пути.

Построим график пути равномерного движения со скоростью По формуле s=vt рассчитаем пройденные в этом движении пути за 1, 2, 3 и т. д. секунды и результаты расчёта запишем в таблицу (стр. 20).

Соответственно данным таблицы на оси времён отложим отрезки, соответствующие 1, 2, 3 секундам (рис. 16). Из концов полученных отрезков проведём перпендикуляры к этой оси и на них отложим пути, пройденные за одну, две и три секунды.

Соединив точки I, II, III, . мы получим прямую (рис. 17), которая называется графиком пути равномерного движения.

Расстояние между любой точкой этой прямой и осью пройденных путей определит промежуток времени, а расстояние между этой точкой и осью времён — путь, пройденный телом в течение этого промежутка времени.

Так, например, расстояние АМ от точки А (рис. 17) до оси пройденных путей соответствует 2,5 сек., а расстояние AN от той же точки до оси времён — отрезку пути в 5 м, следовательно, за 2,5 сек. пройден путь, равный 5 м.

Рис. 17. График пути равномерного движения.

Рис. 18. Графики путей двух равномерных движений.

На рисунке 18 даны графики путей двух равномерных движений, обозначенные цифрами I и II. Скорость какого из этих движений больше? Чтобы ответить на этот вопрос, возьмём на оси времён промежуток времени, изображённый отрезком ОА. Из конца этого отрезка проведём перпендикуляр до пересечения с нашими графиками. Отрезки этого перпендикуляра АС и АВ определят пути, пройденные в течение одного и того же промежутка времени ОА в обоих движениях.

Так как АС больше АВ, то и скорость первого движения больше скорости второго.

График скорости равномерного движения

Рис. 24. График скорости равномерного движения.

Начертим оси координат и на вертикальной оси будем откладывать отрезки, соответствующие в некотором условном масштабе скоростям движения тела. Назовём эту ось осью скоростей (Ov). На другой же оси (оси времён Ot) будем откладывать отрезки, соответствующие промежуткам времени (рис. 24). Так как скорость равномерного движения не меняется со временем, то график её будет представлять собой прямую линию MN, параллельную оси времён. Если взять на этом графике какую-нибудь точку А,
то отрезок прямой АВ между этой точкой и осью времён будет численно равен скорости данного равномерного движения.

Пользуясь графиком скорости, можно определить и путь, пройденный телом за определённый промежуток времени.

Допустим, что велосипедист движется равномерно со скоростью На рисунке 25 изображён график скорости этого
движения в масштабе: 1 см — 1 см—1 сек.

Чтобы найти путь, пройденный велосипедистом в течение,например, 4 сек., необходимо скорость умножить на время, то есть численное значение отрезка 0—3, отложенного на оси скоростей, помножить на численное значение перпендикулярного к нему отрезка 0—4, отложенного на оси времён. В результате мы получим величину площади заштрихованного прямоугольника. Площадь заштрихованного прямоугольника содержит столько же масштабных единиц площади (малый заштрихованный квадрат), сколько метров проехал велосипедист в течение 4 сек.

Рис. 25. Определение пройденного пути по графику скорости.

Таким образом, на графике скорости равномерного движения численное значение пути равно численному значению площади прямоугольника, одна сторона которого равна скорости движения, а другая— времени движения.

Сложение движений

Движение любого тела можно рассматривать как сложное движение, состоящее из нескольких простых движений. Так, например, движение человека по палубе парохода относительно берега можно рассматривать как сложное движение, состоящее из движения человека ‘относительно парохода и движения парохода относительно берега.

Движения человека относительно парохода и парохода относительно берега называются составляющими движениями, а движение человека относительно берега результирующим движением.

Изучив законы составляющих движений, можно установить и закон результирующего движения.

Определение результирующего движения по данным составляющим движениям называется сложением движений.

Рассмотрим движение лодки по течению. Допустим, что под влиянием усилий гребца лодка перемещается относительно воды со скоростью вода же течет относительно берега со скоростью Какое расстояние пройдёт лодка за время t = 5 час.?

Если бы не было течения, то лодка за 5 час. прошла бы вниз по реке расстояние

Одно же течение перенесло бы лодку на расстояние

Но так как лодку одновременно перемешают и гребец и течение, то за 5 час. она пройдёт вниз по реке расстояние:

s = 20 км + 15 км = 35 км.

Что изменится, если скорости останутся по величине такими же, но гребец будет грести против течения?

Очевидно, что лодка под одновременным действием гребца и течения пройдёт те же расстояния, как и в первом случае, но теперь гребец за 5 час. передвинет лодку на расстояние 20 км вверх по реке, а течение за то же время снесёт лодку на расстояние 15 км вниз. В результате лодка, двигаясь по прямой, за 5 час. пройдёт вверх по реке расстояние:

s = 20 км — 15 км = 5 км.

Если путь вверх по реке считать положительным, а вниз — отрицательным, то можно написать, что

s = 20 км + (— 15 км) = 5 км.

В том и другом случае для нахождения пути сложного движения нужно алгебраически сложить пути составляющих движений.

Если бы на лодку действовал ветер в направлении её движения, то очевидно, что путь, пройденный лодкой за то же время, сложился бы из трёх путей составляющих движений (из пути, пройденного под действием гребца, течения и ветра).

Таким же образом можно найти путь, пройденный телом в сложном движении, состоящем из какого угодно числа равномерных движений, направленных по одной прямой.

Если s —путь результирующего движения, a и т. д.—пути составляющих движений, то можно написать:

При этом пути, пройденные в одном направлении, считаются положительными, а пройденные в противоположном — отрицательными.

Если составляющие движения равномерны, то пройденные пути возрастают пропорционально времени. В этом случае и путь результирующего движения, равный сумме путей составляющих движений, также растёт пропорционально времени. Следовательно, и результирующее движение является также равномерным движением.

Итак, результирующее движение, состоящее из нескольких равномерных прямолинейных движений, есть тоже равномерное прямолинейное движение.

Вычислим, чему равна скорость результирующего движения.

Разделим все члены равенства (1) на время движения:

Ho — скорость результирующего движения, a — скорости слагаемых движений; следовательно, равенство (2) можно написать так:

Скорость результирующего движения, состоящего из равномерных прямолинейных движений, равна алгебраической сумме скоростей составляющих движений.

При этом за положительную скорость принимается скорость такого движения, в направлении которого отсчитываются положительные пути, а отрицательной скорости соответствуют отрицательные пути.

Скорость-вектор

Для определения движения недостаточно знать величину пути, пройденного телом, и величину его скорости. Необходимо знать ещё направление движения. Так, например, чтобы определить, где будет находиться самолёт, вылетевший из Москвы со скоростью 400 через 2 часа, необходимо указать, в каком направлении он летел.

Чтобы полностью определить движение тела, условились указывать направление скорости. Для этого скорость изображают отрезком прямой, совпадающим по направлению с направлением движения тела. Стрелка на конце указывает, в какую сторону по этому направлению движется тело. Длина же отрезка в условном масштабе изображает величину скорости.

Величины, определяемые не только своим численным значением, но и направлением в пространстве, называются векторными величинами, или векторами.

Скорость есть вектор.

Рис. 26. Векторы различных скоростей.

Всякий вектор можно изобразить направленным отрезком. На рисунке 26 направленные отрезки прямой изображают две скорости, различные по величине и по направлению. При изучении физики мы встретимся со многими другими векторными величинами.

В отличие от векторных величин существуют величины, которым нельзя приписать никакого направления в пространстве. Они могут отличаться только величиной и иногда знаком. Такие величины называются скалярными, или скалярами.

К скалярным величинам относятся время, температура, масса, работа, энергия и многие другие величины.

Сложение равномерных прямолинейных движений, направленных под углом друг к другу

В некоторых случаях интересующее нас движение мы можем рассматривать как результат сложения нескольких движений, направленных под углом друг к другу. Таково, например, движение лодки поперёк реки или движение самолёта при боковом ветре.

Рассмотрим на примере движения лодки, каким будет результирующее движение двух равномерных и прямолинейных движений, направленных под углом друг к другу.

Рис. 27. Сложение движений лодки и воды.

Если бы течение отсутствовало, то лодка под влиянием усилий гребца перемещалась бы по направлению ОВ (рис. 27), последовательно переходя через равные промежутки времени в положения, обозначенные на чертеже точками и т. д.

Но течение в те же равные промежутки времени перемещает лодку по прямой ОА в положения, обозначенные на рисунке точками и т. д.

Участвуя одновременно в двух движениях, лодка под влиянием усилий гребца за единицу времени пройдёт путь а течением реки за это же время будет отнесена на расстояние то есть действительное движение лодки относительно берега будет происходить по линии ОС через точки и т. д.

Из рисунка видно, что линия ОС представляет собой диагональ параллелограмма ОВСА, стороны которого ОВ и ОД есть пройденные пути в составляющих движениях. Видно также, что пути, проходимые лодкой вдоль диагонали ОС за равные промежутки времени, равны между собой: следовательно, результирующее движение лодки, происходящее по диагонали параллелограмма, есть движение равномерное и прямолинейное.

Эти выводы, полученные нами при рассмотрении движения лодки, справедливы и для всех случаев, когда тело участвует одновременно в двух движениях. Чтобы в этом убедиться, проделаем опыты.

Рис. 28. Сложное движение шарика, подвешенного на нити.

Закрепим на доске конец нити, на которой подвешен небольшой шарик (рис. 28). Подденем под нить у верхнего её конца карандаш и будем двигать его горизонтально вдоль доски, проходя точки Тогда шарик будет одновременно двигаться вертикально вверх и горизонтально. Относительно же доски он будет перемещаться через точки В, С, D, то есть по диагонали прямоугольника, построенного на составляющих
перемещениях как на сторонах.

Если двигать карандаш не горизонтально, а как-нибудь наклонно, например так, как изображено на рисунке 29, то и в этом случае относительно доски шарик будет перемещаться по диагонали параллелограмма.

Рис, 29. Сложное движение шарика, подвешенного на нити.

Итак, опыт показывает, что если тело участвует одновременно в двух равномерных прямолинейных движениях, направленных под углом друг к другу, то результирующее движение его будет равномерное и прямолинейное. Пройденный путь в этом движении изображаете я диагональю параллелограмма, построенного на пройденных путях составляющих движений как на сторонах.

Сложение скоростей

От сложения движений легко перейти к сложению скоростей. Обратимся к рисунку 30.

Рис. 30. Сложение скоростей.

Пусть стороны параллелограмма представляют собой пройденные пути и двух одновременно происходящих равномерных прямолинейных движений за один и тот же промежуток времени, а диагональ параллелограмма — пройденный путь s результирующего движения. Если пройденные пути разделить на время движения t, то получим скорости соответствующих движений:

и

Мы знаем, что направление скорости прямолинейного движения совпадает с
направлением движения (§ 13). Из точки О отложим на направлениях движений векторы этих скоростей. Соединив концы векторов и с концом вектора v прямыми линиями, мы получим параллелограмм

Следовательно, скорость результирующего движения по величине и направлению изображается диагональю параллелограмма, построенного на скоростях составляющих движений как на сторонах.

Этот вывод называется правилом параллелограмма скоростей.

Правило параллелограмма справедливо не только для скоростей, но и для всяких векторов.

Разложение скорости

На рисунке 31 изображён самолёт, поднимающийся вверх под некоторым углом к горизонту со скоростью v.

Допустим, что нам необходимо узнать, с какой скоростью самолёт поднимается вертикально вверх и с какой скоростью он движется в горизонтальном направлении. Представим скорость самолёта, состоящей из скорости, направленной горизонтально, и скорости, направленной вертикально. Для этого воспользуемся правилом параллелограмма. Пусть диагональ в этом параллелограмме изображает вектор скорости самолёта v.

Из начала вектора v проводим две взаимно перпендикулярные линии, одну в вертикальном, другую в горизонтальном направлении. Затем из конца этого вектора проводим линии, параллельные двум заданным направлениям. Они отсекут отрезки, численные значения которых будут равны горизонтальной составляющей скорости и вертикальной

Нахождение по данной скорости её составляющих называется разложением скорости.

Разложение скорости на составляющие обратно действию сложения скоростей.

Так как любую скорость можно рассматривать как результирующую скорость, то, следовательно, любую скорость можно разложить на составляющие.

Рис. 31. Разложение скорости v на горизонтальную — и вертикальную —

Важно подчеркнуть, что данную скорость можно представить в виде диагонали множества параллелограммов с различными сторонами. Следовательно, данную скорость можно разложить на множество пар различных скоростей. В практике чаще всего встречаются случаи разложения скорости на две взаимно перпендикулярные составляющие. Такая задача и была решена нами.

Услуги по физике:

Лекции по физике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.