Уравнение поверхности уровня выводится из

Поверхность равного давления и ее свойства

Поверхностью равного давления (поверхностью уровня) –называется это такая поверхность, во всех точках которой давление имеет одно и то же значение. Поэтому разность давлений в разных точках этой поверхности равна нулю dp = 0. Тогда, исходя из дифференциальных уравнений равновесия жидкости, уравнение поверхности равного давления запишется

.

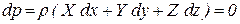(2.36)

где X, Y, Z– ускорения массовых сил.

Поверхность равного давления обладает двумя свойствами.

Рисунок 2.4 —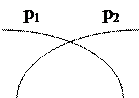

Первое свойство поверхности равного давления — поверхности равного давления не пересекаются между собой. Допустим, что поверхность с давлением p₁ пересекается с поверхностью, на которой давление p₂. Тогда в точках линии пересечения этих поверхностей давление было бы одновременно равным и p₁ и p₂ , что не возможно, т.к. p₁ не равно p₂, следовательно, пересечения этих поверхностей невозможно.

Второе свойство поверхности равного давления — массовые силы направлены перпендикулярно к поверхности равного давления. Доказать это положение можно следующим образом. Рассмотрим вектор массовой силы dF = dm(X i + Y j +Z k) и вектор смещения координаты точки вдоль поверхности равного давления dr = dx i + dy j +dz k. Найдем скалярное произведение этих векторов (dF·dr) = dm (X dx + Y dy +Z dz) =0. Скалярное произведение этих векторов обращается в ноль, так как выполняется уравнение поверхности равного давления (2.36). А скалярное произведение векторов равно нулю, если они перпендикулярны, что и доказывает второе свойство.

Следствие второго свойства поверхности равного давления — в поле силы тяжести в однородной жидкости поверхностью равного давления является любая горизонтальная поверхность. Жидкость называется однородной, если из одной точки жидкости можно перейти в другую точку жидкости не пересекая твердых стенок и других жидкостей. Действительно, сила тяжести направлена вниз, поэтому поверхность равного давления должна быть горизонтальной.

Дата добавления: 2015-04-18 ; просмотров: 408 ; Нарушение авторских прав

Тема 5 Поверхность уровня

Поверхностью уровня называется такая поверхность, все точки которой имеют одно и то же значение рассматриваемой функции: например, поверхность равной температуры (изотермическая поверхность), поверхность равного потенциала и т.д. Для рассмотрения задач гидрогазодинамики особое значение имеет поверхность равного давления, которую кратко будем называть поверхностью уровня.

Поверхность, во всех точках которой давление жидкости одинаково называется поверхностью равного давления (или поверхностью уровня).

Так как во всех точках поверхности уровня гидростатическое давление одинаково р = const, то изменение давления dp = 0. Из основного уравнения гидростатики (4.6) dp = r × (X × dx + Y × dy + Z × dz) получим

r × (X × dx + Y × dy + Z × dz) = 0.

Так как плотность r ¹ 0, то

X × dx + Y × dy + Z × dz = 0. (5.1)

где X, Y и Z – проекции ускорения массовой (объёмной при r = const) силы на координатные оси.

Уравнение (5.1) представляет собой дифференциальное уравнение поверхности равного давления, то есть уравнение поверхности уровня.

Свойства поверхности уровня

1. Две поверхности уровня не пересекаются между собой.

Действительно, допустим, что поверхность давления р₁ пересекается с поверхностью давления р₂. Тогда в точках линии пересечения этих поверхностей давление должно быть одновременно равным и р₁ и р₂, что невозможно, так как р₁ ¹ р₂. Следовательно, пересечение этих поверхностей невозможно.

2. Внешние массовые (объёмные) силы направлены нормально к поверхности уровня.

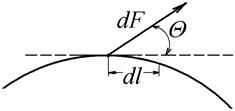
Доказать это положение можно следующим образом. Работа силы dF на элементарном пути dl равна: dА = r × (X × dx + Y × dy + Z × dz). Но для поверхности уровня трёхчлен в скобках равен нулю, поэтому работа силы dF на пути dl вдоль поверхности уровня равна нулю (dА = 0).

С другой стороны, согласно рис. 8 работа силы dF равна dА = dF × cosQ × dl. Поскольку dА = 0, а dF ¹ 0 и dl = 0, то cosQ должен быть равен нулю, то есть угол Q = .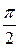

Рассмотрим равновесие капельной и газообразной жидкости в поле земного тяготения в пределах небольшой ограниченной области. Ускорения свободного падения в различных точках этого пространства будут параллельны и направлены вертикально вниз. Расположим координатную ось 0z вертикально вверх. При этом ускорение свободного падения g = 9,81 м/с 2 будет направлено параллельно оси 0z.

Составим уравнение поверхности уровня, учитывая, что для данного случая равновесия жидкости величины X, Y и Z будут равны соответственно:

Подставляя эти значения в дифференциальное уравнение поверхности уровня (5.1) X × dx + Y × dy + Z × dz = 0 получим дифференциальное уравнение поверхности уровня для рассматриваемых условий:

– g × dz = 0 или dz = 0. (5.2)

Интегрируя это уравнение, находим

Так как С = const – произвольная постоянная, то это уравнение (5.3) будет уравнением семейства горизонтальных плоскостей, параллельным осям 0x и 0y,

Итак, ели на жидкость действует только сила тяжести, поверхность уровня есть горизонтальная плоскость.

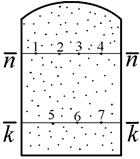
Следовательно, в пределах любой горизонтальной плоскости, проведенной через область, занятую покоящимся газом, давление остаётся неизменным (рис. 9). При равновесии газа гидростатическое давление в точке р изменяется только с высотой расположения этой точки р = f(z).

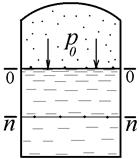
Если закрытый резервуар заполнен капельной жидкостью, то во всех точках свободной поверхности гидростатическое давление одинаково р₀ (рис. 10). Свободная поверхность воды в открытом резервуаре испытывает одно и то же атмосферное давление р_бар. Свободная поверхность в этих случаях является поверхностью уровня и, следовательно, горизонтальной плоскостью. В условиях равновесия поверхность уровня неподвижна.

Рисунок 9 Рисунок 10

Волновая поверхность водоёма также есть поверхность уровня р_бар, но волновая поверхность изменяется во времени, то есть подвижна.

Проведём произвольную горизонтальную плоскость n – n (рис. 10). Эта плоскость также будет поверхностью уровня. Во всех точках этой плоскости давление будет одинаковым.

Так как плоскости n – n и свободной поверхности параллельны между собой, то все точки плоскости n – n находятся на одной и той же глубине. Следовательно, величина гидростатического давления зависит только от глубины погружения точки под уровень свободной поверхности и на одинаковой глубине гидростатическое давление в любой точке будет одним и тем же.

Этот вывод является выражением следствия из закона Паскаля.

Следствие из закона Паскаля: на данном горизонтальном уровне внутри покоящейся жидкости давление во всех точках одинаково.

Тема 6 Распределение гидростатического давления (Интегрирование уравнения Эйлера)

Воспользуемся основным дифференциальным уравнением гидростатики (4.6)

dp = r × (X × dx + Y × dy + Z × dz).

В случае равновесия несжимаемой жидкости в поле земного тяготения проекции ускорения массовой силы (силы тяжести) X, Y и Z на координатные оси 0x, 0y и 0z (ось 0z направлена вертикально вверх) равны соответственно:

Тогда из основного дифференциального уравнения гидростатики (4.6) имеем:

dp = – r × g × dz

+ dz = 0. (6.1)

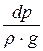
Интегрируя (6.1) при r = const, имеем

+ z = С, (6.2)

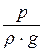
где С – постоянная интегрирования.

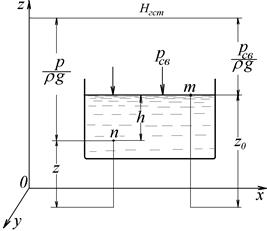
Для определения постоянной интегрирования С рассмотрим резервуар, заполненный жидкостью (рис. 12).

Для точки m, лежащей на свободной поверхности жидкости р = р_св и z = z₀. Подставляя эти значения в (6.2) находим, что

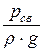
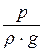
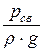
С = + z₀.

+ z = + z₀

где h – глубина погружения рассматриваемой точки под уровень свободной поверхности жидкости.

Окончательно основное уравнение гидростатики (в интегральной форме) имеет вид:

где р – полное (или абсолютное) давление в рассматриваемой точке;

р_св – давление на свободную поверхность жидкости (внешнее давление). Часто обозначается р₀;

r × g × h – относительное (или весовое) давление. Эта величина равна весу столба жидкости при единичной площади и высоте h.

Общий гидростатический закон может быть сформулирован следующим образом: давление в любой точке покоящейся жидкости равно внешнему давлению, сложенному с весом столба жидкости высотой от поверхности до данной точки с площадью основания, равной единице.

Иначе можно сказать, что абсолютное (полное) давление в рассматриваемой точке равно внешнему давлению, сложенному с давлением столба жидкости над точкой.

Если абсолютное давление в рассматриваемой точке р больше атмосферного р_бар, то разность (р – р_бар) представляет собой превышение полного давления над атмосферным и называется манометрическим или избыточным давлением в данной точке:

Если давление на свободной поверхности жидкости равно атмосферному (р_св = р_бар), то

В этом случае избыточное и весовое давление совпадают.

Если абсолютное давление в точке меньше атмосферного, то недостача абсолютного давления до атмосферного называется вакуумом или разрежением:

Линии и поверхности уровня

Содержание:

Линии и поверхности уровня

Понятие линии и поверхности уровня:

Для характеристики функций двух переменных вводится понятие линий уровня.

Определение 2. Линией уровня функции z = f (x, y) называется совокупность всех точек на плоскости Oxy, для которых выполняется условие f (x, y) = C.

Линии уровня можно получить, пересекая поверхность z = f (x, y) плоскостями z = C, где С = соnst.

Пример 1. Найти линии уровня функции z = x 2 + y 2 .

Решение.
Пусть z = C. x 2 + y 2 = C (C ≥ 0),

В этом случае линиями уровня является множество концентрических окружностей с центром в начале координат и радиусом С (рис. 2) .Аналогично вводится понятие поверхности уровня для функции трех переменных u = f (x, y, z), (f (x, y, z) = C).

Пример 2. Найти поверхности уровня функции u = x 2 + y 2 + z 2 .

Решение. Пусть u = C. Тогда x 2 + y 2 + z 2 = C (C ≥ 0) — это множество сфер с центром в точке O(0; 0; 0) и радиусом C.

Поверхности второго порядка

Наиболее изучены поверхности в курсе аналитической геометрии — поверхности второго порядка. В общем случае уравнение такой поверхности имеет вид:
a₁₁ x 2 + 2a₁₂ xy + a₂₂ y 2 + 2a₁₃ xz + 2a₂₃ yz + a₃₃ z 2 + 2a₁₄ x + 2a₂₄ y + 2a₃₄ z + a₄₄ = 0.

В зависимости от значений коэффициентов получают различные поверхности второго порядка.

Например:
1) — конус;

2) — полусфера;

Рис. 4.

3) — эллиптический параболоид;

Рис. 5.

4) — гиперболический параболоид;

рис.6

5) — трехосный эллипсоид.

Рис. 7.

Для изучения поверхностей в трехмерном пространстве применяется метод сечений. Суть этого метода такова: пересекаем заданную поверхность плоскостями x = C₁, y = C₂, z = C₃. В результате получим некоторые кривые, характеризующие поверхность.

Пример 3. z = x 2 + y 2 . Пусть z = C₁ (C₁ ≥ 0). Получим уравнение x 2 + y 2 = C₁ (уравнение окружности). Положим y = C₂ , тогда — уравнение параболы в плоскости Оxz, которая смещена на единиц вверх по оси Oz. Положим x = C₃ , получим уравнение
Получили уравнение параболы в плоскости Оyz, которая смещена на единиц вверх по оси Оz. Из этих исследований вытекает, что графиком функции z = x 2 + y 2 является параболоид вращения вокруг оси Оz.

Гиперповерхности уровня

Пусть задана функция от n переменных u = f (x₁, x₂, . x_n) . Если положить u = C, то получим уравнение f (x₁, x₂, . x_n) = C, которое называется уравнением гиперповерхности уровня в пространстве R n . Например: Если u = C, то уравнение является уравнением гиперсферы в R n с центром в точке O (0,0, . 0) и радиусом .

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.