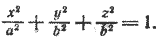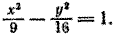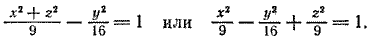Уравнение поверхности вращения линии вокруг оси

Уравнение поверхности вращения линии вокруг оси

Глава VI. Простейшие криволинейные поверхности и тела вращения.

§ 75*. Поверхности вращения

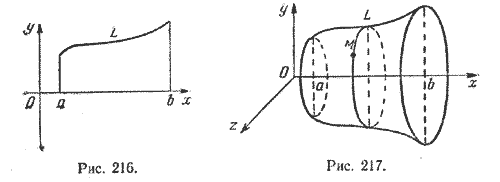
1. Пусть в плоскости р задана кривая L и некоторая прямая l. Поверхность, которая получается вращением кривой L вокруг прямой l, называется поверхностью вращения.

Пусть кривая L лежит в плоскости хОу (рис. 216) и имеет уравнение

y = f(x), х [а; b]. (1)

Найдем уравнение поверхности, которая получится вращением кривой L вокруг оси Ох (рис. 217).

Очевидно, точка M с координатами (х; у; z), где х [а; b], принадлежит искомой поверхности вращения тогда и только тогда, когда

Действительно, точки (х; у; z) и (х; f(x); 0) лежат на одной окружности с центром в точке (х; 0; 0).

Таким образом, уравнение поверхности, полученной вращением кривой (1) вокруг оси Ох, имеет вид

y 2 + z 2 = (f(x)) 2 , х [а; b]. (2)

Заметим, что уравнение (2) получается из уравнения (1) следующим образом:
обе части уравнения (1) возводятся в квадрат и y 2 заменяется на y 2 + z 2 ,

В частности, если кривая L задана уравнением

то уравнение поверхности, полученной вращением этой кривой вокруг оси Ох, имеет вид

т. е. просто y 2 заменяем на y 2 + z 2 .

2. Поверхность, которая получается вращением эллипса вокруг одной из его осей, называется эллипсоидом вращения.

Пусть в плоскости хОу эллипс задан уравнением

(5)

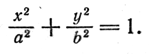
Составим уравнение поверхности, полученной вращением его вокруг оси Ох. Уравнение эллипса (5) приводится к виду (3), следовательно, для получения уравнения эллипсоида вращения достаточно в уравнении (5) y 2 заменить на y 2 + z 2 . После замены получим

(6)

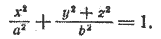
Это уравнение обычно записывают так:

При а > b уравнение (6) определяет эллипсоид вращения, вытянутый вдоль оси Ох (рис. 218), при а 2 на y 2 + z 2 , получим искомое уравнение эллипсоида вращения:

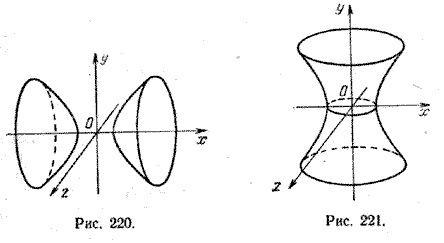
3. Поверхность, которая получается вращением гиперболы вокруг одной из ее осей, называется гиперболоидом вращения. При вращении гиперболы вокруг ее действительной оси получается двуполостный гиперболоид вращения (рис. 220), а при вращении гиперболы вокруг ее мнимой оси получается однополостный гиперболоид вращения (рис. 221).

Пусть в плоскости хОу гипербола задана уравнением

(7)

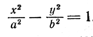
Составим уравнение поверхности, полученной вращением гиперболы вокруг ее действительной оси Ох. Уравнение гиперболы (7) приводится к виду (3); следовательно, для получения уравнения поверхности двуполостного гиперболоида вращения достаточно в уравнении гиперболы (7) y 2 заменить на y 2 + z 2 . После замены получим

(8)

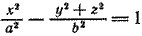
При вращении гиперболы (7) вокруг ее мнимой оси нужно в уравнении (7) x 2 заменить на x 2 + z 2 ; после замены получим

(9)

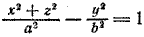
Задача 2. Гипербола с полуосями а = 3 и b = 4 вращается вокруг своей мнимой оси, совпадающей с осью Оу. Центр гиперболы совпадает с началом координат. Составить уравнение поверхности, полученной при вращении этой гиперболы.

Составим уравнение гиперболы:

Чтобы получить уравнение гиперболоида вращения, в уравнении гиперболы x 2 заменим на x 2 + z 2 . После замены получим

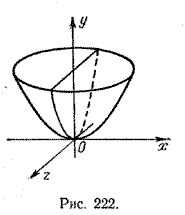
4. Поверхность, которая получается вращением параболы вокруг ее оси симметрии, называется параболоидом вращения (рис. 222).

Пусть на плоскости хОу парабола задана уравнением

Для получения уравнения поверхности вращения нужно в уравнении (10) x 2 заменим на x 2 + z 2 ; после замены получим

Отметим одно замечательное свойство этой поверхности. Если внутреннюю поверхность параболоида вращения сделать зеркальной, а в ее фокусе (фокусом параболоида вращения называется фокус вращаемой параболы) поместить источник света, то все лучи света, отражаясь от поверхности параболоида, пойдут параллельно оси параболоида.

Это свойство широко используется при изготовлении светоотражающих устройств (прожекторов, фар автомобиля, кинопроекторов и других приборов).

Задача 3. Составить уравнение поверхности, полученной вращением параболы y 2 = 2х вокруг оси Ох.

Чтобы составить уравнение параболоида вращения, полученного вращением параболы вокруг оси Ох, нужно в уравнении y 2 = 2х заменить y 2 на y 2 + z 2 , после замены получим

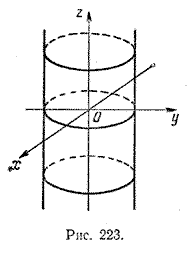
5. Если вращать прямую, параллельную какой-либо оси координат, вокруг этой оси, то получится круговая цилиндрическая поверхность.

Пусть дана прямая, лежащая в плоскости yOz и имеющая уравнение у = а. Легко видеть, что поверхность вращения этой прямой вокруг оси Oz имеет уравнение

Эта цилиндрическая поверхность изображена на рис. 223.

Задача 4. Составить уравнение цилиндрической поверхности, полученной вращением прямой у = 3, лежащей в плоскости хОу вокруг оси Ох.

В уравнении y 2 = 3 2 заменим y 2 на y 2 + z 2 , в результате получим

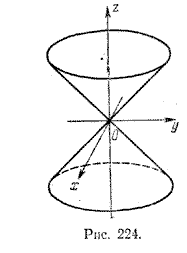
6. Пусть дана прямая, лежащая в плоскости yOz и проходящая через начало координат:
y = kz, k =/= 0.

Очевидно, уравнение поверхности вращения этой прямой вокруг оси Oz имеет вид

Полученное уравнение является уравнением искомой поверхности вращения, которая называется круговой конической поверхностью (рис. 224).

Задача 5. Составить уравнение поверхности вращения прямой 2х = 3у, z =0 вокруг оси Ох.

Из уравнения 3у = 2х, используя формулу (2), находим 9(y 2 + z 2 ) = 4x 2 . Это и есть искомое уравнение.

Уравнение поверхности вращения линии вокруг оси

Рассмотрим сечение плоскостью у = 0. Получается парабола = z, её ветви направлены вверх, вершина в точке (0, 0, 0).

Рассмотрим сечение плоскостью x = h. Это опять парабола:

Её ветви направлены вниз, вершина смещена по оси OZ на величину . то есть находится в точке . Заметим, что эта точка лежит на параболе

Теперь, изменяя h, видим, что поверхность гиперболического параболоида состоит из парабол, расположенных в плоскостях x = h, вершины которых находятся на параболе .

Поверхности второго порядка

Поверхности вращения.

Поверхность \(S\) называется поверхностью вращения с осью \(d\), если она составлена из окружностей, которые имеют центры на прямой \(d\) и лежат в плоскостях, перпендикулярных данной прямой.

Рассмотрим линию \(L\), которая лежит в плоскости \(P\), проходящей через ось вращения \(d\) (рис. 43), и будем вращать ее вокруг этой оси. Каждая точка линии опишет окружность, а вся линия — поверхность вращения.

Рис. 10.1. Поверхность вращения.

Выберем начало декартовой прямоугольной системы координат \(O, \boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>\) на оси \(d\), вектор \(\boldsymbol_<3>\) направим вдоль \(d\), а вектор \(\boldsymbol_<1>\) поместим в плоскости \(P\). Таким образом, \(O, \boldsymbol_<1>, \boldsymbol_<3>\) — декартова система координат в плоскости \(P\). Пусть линия \(L\) имеет в этой системе координат уравнение \(f(x, y)=0\).

Рассмотрим точку \(M(x, y, z)\). Через нее проходит окружность, которая имеет центр на оси \(d\) и лежит в плоскости, перпендикулярной этой оси. Радиус окружности равен расстоянию от \(M\) до оси, то есть \(\sqrt+y^<2>>\). Точка \(M\) лежит на поверхности вращения тогда и только тогда, когда на указанной окружности имеется точка Мь принадлежащая вращаемой линии \(L\).

Точка \(M_<1>(x_<1>, y_<1>, z_<1>)\) лежит в плоскости \(P\), и потому \(y_<1>=0\). Кроме того, \(z_<1>=z\) и \(|x|=\sqrt+y^<2>>\), так как \(M_<1>\) лежит на той же окружности, что и \(M\). Координаты точки \(M_<1>\) удовлетворяют уравнению линии \(L\): \(f(x_<1>, z_<1>)=0\). Подставляя в это уравнение \(x_<1>\) и \(z_<1>\), мы получаем условие на координаты точки \(M\), необходимое и достаточное для того, чтобы \(M\) лежала на поверхности вращения \(S\): равенство
$$
f\left(\pm \sqrt+y^<2>>, z\right)=0\label
$$
должно быть выполнено хотя бы при одном из двух знаков перед корнем. Это условие, которое можно записать также в виде
$$
f\left(\sqrt+y^<2>>, z\right)f\left(-\sqrt+y^<2>>, z\right)=0,\label
$$
и является уравнением поверхности вращения линии \(L\) вокруг оси \(d\).

Эллипсоид.

Рассмотрим поверхности, которые получаются при вращении эллипса вокруг его осей симметрии. Направив вектор \(\boldsymbol_<3>\) сначала вдоль малой оси эллипса, а затем вдоль большой оси, мы получим уравнения эллипса в следующих видах:
$$
\frac>>+\frac>>=1,\ \frac>>+\frac>>=1.\nonumber
$$
(Здесь через \(c\) обозначена малая полуось эллипса.) В силу формулы \eqref уравнениями соответствующих поверхностей вращения будут
$$
\frac+y^<2>>>+\frac>>=1,\ \frac>>+\frac+y^<2>>>=1\ (a > c).\label
$$
Поверхности с такими уравнениями называются соответственно сжатым и вытянутым эллипсоидами вращения (рис. 10.2).

Рис. 10.2. Сжатый (а) и вытянутый (б) эллипсоиды вращения.

Каждую точку \(M(x, y, z)\) на сжатом эллипсоиде вращения сдвинем к плоскости \(y=0\) так, чтобы расстояние от точки до этой плоскости уменьшилось в постоянном для всех точек отношении \(\lambda Рис. 10.3. Эллипсоид.

Эллипсоид так же, как и эллипсоид вращения, из которого он получен, представляет собой замкнутую ограниченную поверхность. Из уравнения \eqref видно, что начало канонической системы координат — центр симметрии эллипсоида, а координатные плоскости — его плоскости симметрии.

Эллипсоид можно получить из сферы \(x^<2>+y^<2>+z^<2>=a^<2>\) сжатиями к плоскостям \(y=0\) и \(z=0\) в отношениях \(\lambda=b/a\) и \(\mu=c/a\).

В этой статье нам часто придется прибегать к сжатию, и мы не будем его каждый раз описывать столь подробно.

Конус второго порядка.

Рассмотрим на плоскости \(P\) пару пересекающихся прямых, задаваемую в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<3>\) уравнением \(a^<2>x^<2>-c^<2>z^<2>=0\). Поверхность, получаемая вращением этой линии вокруг оси аппликат, имеет уравнение
$$
a^<2>(x^<2>+y^<2>)-c^<2>z^<2>=0\label
$$
и носит название прямого кругового конуса (рис. 10.4). Сжатие к плоскости \(y=0\) переводит прямой круговой конус в поверхность с уравнением
$$
a^<2>x^<2>+b^<2>y^<2>-c^<2>z^<2>=0\label
$$
называемую конусом второго порядка.

Обратите внимание на то, что левая часть уравнения \eqref — однородная функция, и поверхность является конусом в смысле определения, введенного ранее.

Рис. 10.4. Прямой круговой конус.

Однополостный гиперболоид.

Однополостный гиперболоид вращения — это поверхность вращения гиперболы
$$
\frac>>-\frac>>=1\nonumber
$$
вокруг той оси, которая ее не пересекает. По формуле \eqref мы получаем уравнение этой поверхности (рис. 10.5)
$$
\frac+y^<2>>>-\frac>>=1.\label
$$

Рис. 10.5. Однополостный гиперболоид вращения.

В результате сжатия однополостного гиперболоида вращения к плоскости \(y=0\) мы получаем однополостный гиперболоид с уравнением
$$
\frac>>+\frac>>-\frac>>=1.\label
$$

Интересное свойство однополостного гиперболоида — наличие у него прямолинейных образующих. Так называются прямые линии, всеми своими точками лежащие на поверхности. Через каждую точку однополостного гиперболоида проходят две прямолинейные образующие, уравнения которых можно получить следующим образом.

Покажем на примере, как найти образующие, проходящие через данную точку поверхности. Рассмотрим поверхность \(x^<2>+y^<2>-z^<2>=0\) и точку \(M_<0>(1, 1, 1)\) на ней. Подставляя координаты \(M_<0>\) в уравнения \eqref, мы получаем условия на \(\lambda\) и \(\mu\): \(2\lambda=2\mu\) и \(0 \cdot \lambda=0 \cdot \mu\). Первое из них определяет \(\lambda\) и \(\mu\) с точностью до общего множителя, но только с такой точностью они и нужны. Подставляя эти значения в \eqref, получаем уравнения прямолинейной образующей
$$
x+z=1+y,\ x-z=1-y.\nonumber
$$

Она проходит через \(M_<0>\), так как \(\lambda\) и \(\mu\) так и выбирались, чтобы координаты \(M_<0>\) удовлетворяли этой системе. Аналогично, подставляя координаты \(M_<0>\) в (10), находим условия на \(\lambda’\) и \(\mu’\): \(2\mu’=0\) и \(2\mu’=0\). Коэффициент \(\lambda’\) можно взять любым ненулевым, и мы приходим к уравнению второй образующей: \(x=z\), \(y=1\).

Если вместе с гиперболой мы будем вращать ее асимптоты, то они опишут прямой круговой конус, называемый асимптотическим конусом гиперболоида вращения. При сжатии гиперболоида вращения его асимптотический конус сжимается в асимптотический конус общего однополостного гиперболоида.

Двуполостный гиперболоид.

Двуполостный гиперболоид вращения — это поверхность, получаемая вращением гиперболы
$$
\frac>>-\frac>>=1\nonumber
$$
вокруг той оси, которая ее пересекает. По формуле \eqref мы получаем уравнение двуполостного гиперболоида вращения
$$
\frac>>-\frac+y^<2>>>=1.\label
$$
В результате сжатия этой поверхности к плоскости у=0 получается поверхность с уравнением
$$
\frac>>-\frac>>-\frac>>=1.\label
$$

Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение вида \eqref, называется двуполостным гиперболоидом (рис. 10.6). Двум ветвям гиперболы здесь соответствуют две не связанные между собой части (“полости”) поверхности, в то время как при построении однополостного гиперболоида вращения каждая ветвь гиперболы описывала всю поверхность.

Асимптотический конус двуполостного гиперболоида определяется так же, как и для однополостного.

Рис. 10.6. Двуполостный гиперболоид вращения.

Эллиптический параболоид.

Вращая параболу \(x^<2>=2pz\) вокруг ее оси симметрии, мы получаем поверхность с уравнением
$$
x^<2>+y^<2>=2pz.\label
$$
Она называется параболоидом вращения. Сжатие к плоскости \(y=0\) переводит параболоид вращения в поверхность, уравнение которой приводится к виду
$$
\frac>>+\frac>>=2z.\label
$$

Поверхность, которая имеет такое уравнение в некоторой декартовой прямоугольной системе координат, называется эллиптическим параболоидом (рис. 10.7).

Рис. 10.7. Эллиптический параболоид.

Гиперболический параболоид.

По аналогии с уравнением \eqref мы можем написать уравнение
$$
\frac>>-\frac>>=2z.\label
$$

Поверхность, которая имеет уравнение вида \eqref в некоторой декартовой прямоугольной системе координат, называется гиперболическим параболоидом.

Исследуем форму этой поверхности. Для этого рассмотрим ее сечение плоскостью \(x=\alpha\) при произвольном \(\alpha\). В этой плоскости выберем декартову прямоугольную систему координат \(O’, \boldsymbol_<2>, \boldsymbol_<3>\) с началом в точке \(O'(\alpha, 0, 0)\). Относительно этой системы координат линия пересечения имеет уравнение
$$
-\frac>>=2\left(z-\frac<\alpha^<2>><2a^<2>>\right).\label
$$
Эта линия — парабола, в чем легко убедиться, перенеся начало координат в точку \(O″\) с координатами \((0, \alpha^<2>/(2a^<2>))\). (Координаты этой точки относительно исходной системы координат \(O, \boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>\) в пространстве равны \((\alpha, 0, \alpha^<2>/(2a^<2>))\).)

Точка \(O″\), очевидно, является вершиной параболы, ось параболы параллельна вектору \(\boldsymbol_<3>\), а знак минус в левой части равенства \eqref означает, что ветви параболы направлены в сторону, противоположную направлению \(\boldsymbol_<3>\). Заметим, что после переноса начала координат в точку \(O″\) величина а не входит в уравнение параболы, и, следовательно, сечения гиперболического параболоида плоскостями \(x=\alpha\) при всех \(\alpha\) представляют собой равные параболы.

Будем теперь менять величину \(\alpha\) и проследим за перемещением вершины параболы \(O″\) в зависимости от \(\alpha\). Из приведенных выше координат точки \(O″\) следует, что эта точка перемещается по линии с уравнениями
$$
z=\frac><2a^<2>>,\ y=0\nonumber
$$
в системе координат \(O, \boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>\). Эта линия — парабола в плоскости \(y=0\). Вершина параболы находится в начале координат, ось симметрии совпадает с осью аппликат, а ветви параболы направлены в ту же сторону, что и вектор \(\boldsymbol_<3>\).

Теперь мы можем построить гиперболический параболоид следующим образом: зададим две параболы и будем перемещать одну из них так, чтобы ее вершина скользила по другой, оси парабол были параллельны, параболы лежали во взаимно перпендикулярных плоскостях и ветви их были направлены в противоположные стороны.

При таком перемещении подвижная парабола описывает гиперболический параболоид (рис. 10.8).

Рис. 10.8. Гиперболический параболоид. \(OB\) — неподвижная парабола, \(KLM,\ NOP,\ QRS\) — положения подвижной параболы.

Сечения гиперболического параболоида плоскостями с уравнениями \(z=\alpha\) при всевозможных \(\alpha\) — гиперболы. Эти сечения нарисованы на рис. 10.9.

Рис. 10.9. Сечения гиперболического параболоида

Выводятся эти уравнения так же, как и уравнения прямолинейных образующих однополостного гиперболоида.

Рис. 10.10. Прямолинейные образующие гиперболического параболоида