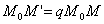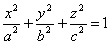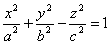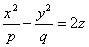Уравнение поверхности второго порядка параболоид

Поверхности второго порядка: их виды, уравнения, примеры

Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат

Общее уравнение поверхности второго порядка имеет вид

Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты — это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:

Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:

В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.

Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому

I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 , λ 2 , λ 3 — корни характеристического уравнения

.

В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.

Эллипсоид

Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.

После решения характеристического уравнения общее уравнение можно переписать в следующем виде:

.

Тогда полуоси эллипсоида будут

, , .

Поэтому каноническое уравнение эллипсоида имеет вид

.

Мнимый эллипсоид

Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:

,

, , .

Мнимый конус

Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:

,

, , .

Однополостный гиперболоид

Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:

.

, , ,

то каноническое уравнение однополостного гиперболоида будет иметь вид

.

Двуполостный гиперболоид

Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:

.

Последняя запись и есть каноническое уравнение двуполостного гиперболоида.

Конус

Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.

Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:

,

известном как каноническое уравнение конуса.

II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.

Эллиптический параболоид

Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.

Общее уравнение можно переписать в виде:

.

Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая

,

,

получим каноническое уравнение эллиптического параболоида:

.

Гиперболический параболоид

Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.

Обозначая через λ 1 положительный корень, а через λ 2 — отрицательный и беря перед корнем знак минус, переписываем уравнение в виде:

.

, ,

получим каноническое уравнение гиперболического параболоида:

.

III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.

Эллиптический цилиндр

Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

, ,

получим каноническое уравнение эллиптического цилиндра:

.

Мнимый эллиптический цилиндр

Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

Последняя запись — каноническое уравнение мнимого эллиптического цилиндра.

Мнимые пересекающиеся плоскости

Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

, ,

получим каноническое уравнение мнимых пересекающихся плоскостей:

.

Гиперболический цилиндр

Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

,

, .

Таким образом, каноническое уравнение гиперболического цилиндра:

.

Пересекающиеся плоскости

Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

,

, .

Таким образом, пересекающихся плоскостей:

.

IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 = I 1 — отличный от нуля корень характеристического уравнения.

Параболический цилиндр

Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:

,

.

Это уравнение параболического цилиндра, в каноническом виде оно записывается так:

.

V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

.

Параллельные плоскости

Если K 2 , то общее уравнение поверхности второго порядка определяет две параллельные плоскости.

,

перепишем его в виде

.

Мнимые параллельные плоскости

Если K 2 > 0 , то общее уравнение поверхности второго порядка определяет две мнимые параллельные плоскости.

,

перепишем его в виде

.

Совпадающие плоскости

Если K 2 = 0 , то общее уравнение поверхности второго порядка определяет две совпадающие плоскости:

.

Решение примеров на определение вида поверхности второго порядка

Пример 1. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Решение. Найдём I 3 :

(как вычислить определитель).

I 1 = 1 + 5 + 1 = 7 ,

Следовательно, данная поверхность — однополостный гиперболоид.

.

Составляем и решаем характеристическое уравнение:

;

.

,

, , .

Пример 2. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Решение. Найдём I 3 :

.

.

Следовательно, общее уравнение определяет эллиптический параболоид.

.

I 1 = 2 + 2 + 3 = 7 .

Решаем характеристическое уравнение:

.

.

,

, .

Пример 3. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

,

,

,

I 1 = 5 + 2 + 5 = 12 .

Так как I 3 = К 4 = 0 , I 2 > 0 , I 1 K 3 , то данное общее уравнение определяет эллиптический цилиндр.

.

.

Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение

Пример 4. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Параболоиды: определение, виды, сечения

Определение параболоида

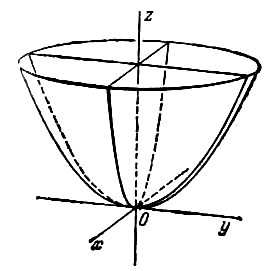
Эллиптическим параболоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением

Гиперболическим параболоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением

В уравнениях (4.51) и (4.52) и — положительные параметры, характеризующие параболоиды, причем для эллиптического параболоида .

Начало координат называют вершиной каждого из параболоидов ((4.50) или (4.51)).

Плоские сечения эллиптического параболоида

Плоскость пересекает эллиптический параболоид (4.51) по линии, имеющей в этой плоскости уравнение , которое равносильно уравнению параболы с фокальным параметром . Сечение параболоида плоскостью получаем, подставляя в уравнение (4.51): . Это уравнение равносильно уравнению параболы с фокальным параметром . Эти сечения называются главными параболами эллиптического параболоида (4.51).

Рассмотрим теперь сечение эллиптического параболоида плоскостями, параллельными плоскости . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.51), получаем

При уравнение не имеет действительных решений, т.е. плоскость при не пересекает параболоид (4.51). При уравнению (4.51) удовлетворяет одна вещественная точка — вершина параболоида. При 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> уравнение определяет эллипс с полуосями . Следовательно, сечение эллиптического параболоида плоскостью (при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» />) представляет собой эллипс, центр которого лежит на оси аппликат, а вершины — на главных параболах.

Таким образом, эллиптический параболоид можно представить как поверхность, образованную эллипсами, вершины которых лежат на главных параболах (рис.4.46,а).

Параболоид вращения

Эллиптический параболоид, у которого , называется параболоидом вращения . Такой параболоид является поверхностью вращения. Сечения параболоида вращения плоскостями (при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» />), представляют собой окружности с центрами на оси аппликат (рис.4.46,б). Его можно получить, вращая вокруг оси параболу , где .

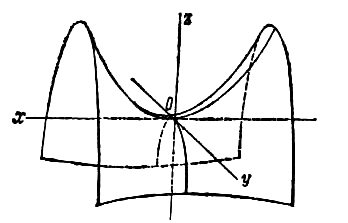
Плоские сечения гиперболического параболоида

Сечения гиперболического параболоида координатными плоскостями и представляют собой параболы (главные параболы) или с параметрами или соответственно. Поскольку оси симметрии главных парабол направлены в противоположные стороны, гиперболический параболоид называют седловой поверхностью .

Рассмотрим теперь сечения гиперболического параболоида плоскостями, параллельными плоскости . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.52), получаем При 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> уравнение равносильно уравнению гиперболы полуосями , то есть сечение гиперболического параболоида плоскостью при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> представляет собой гиперболу с центром на оси аппликат, вершины которой лежат на главной параболе . При получаем уравнение сопряженной гиперболы с полуосями , т.е. сечение гиперболического параболоида плоскостью при представляет собой сопряженную гиперболу с центром на оси аппликат, вершины которой лежат на главной параболе . При получаем уравнение пересекающихся прямых , т.е. сечение гиперболического параболоида плоскостью представляет собой пару пересекающихся в начале координат прямых.

Таким образом, гиперболический параболоид можно представить как поверхность, образованную гиперболами (включая и «крест» из их асимптот), вершины которых лежат на главных параболах (рис.4.47,а).

Сечение параболоида плоскостью , где — произвольная постоянная, представляет собой параболу

равную главной параболе с параметром , вершина которой лежит на другой главной параболе с параметром . Поэтому гиперболический параболоид можно представить как поверхность, получающуюся при перемещении одной главной параболы так, чтобы ее вершина «скользила» по другой главной параболе (рис.4.47,б).

1. Гиперболический параболоид является линейчатой поверхностью, т.е. поверхностью, образованной движением прямой (рис.4.47,в).

2. Ось аппликат канонической системы координат является осью симметрии параболоида, а координатные плоскости — плоскостями симметрии параболоида.

В самом деле, если точка принадлежит параболоиду (эллиптическому или гиперболическому), то точки с координатами при любом выборе знаков также принадлежат параболоиду, поскольку их координаты удовлетворяют уравнению (4.51) или (4.52) соответственно. Поэтому параболоид симметричен относительно координатных плоскостей и координатной оси .

Уравнение поверхности второго порядка параболоид

Глава 46. Поверхности второго порядка

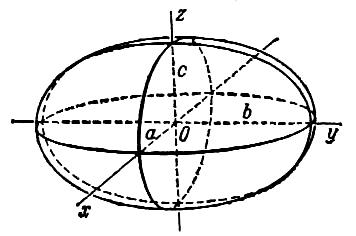
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

(1).

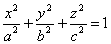
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.

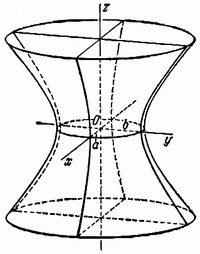
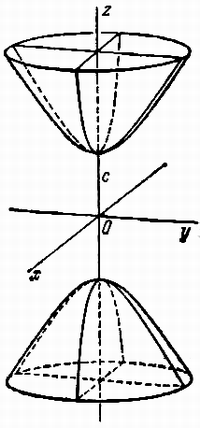
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

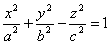
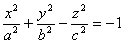
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

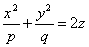
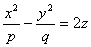
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости , — основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство

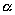
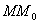
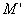
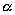
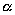
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .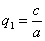

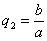
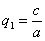
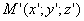
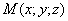
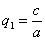
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть — точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .

Таким образом, мы получаем искомые выражения:

, , (6)

, , (7)

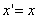
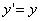
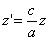
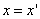
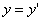
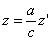
Предположим, что M(x; y; z ) — произвольная точка сферы

.

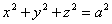
Заменим здесь x, y, z их выражениями (7); получим

,

.

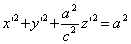
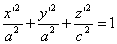
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

, , ;

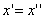
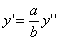
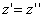
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

имеет две системы прямолинейных образующих, которые определяются уравнениями:

, ;

, ,

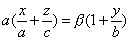
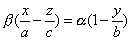
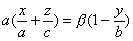
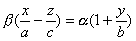
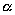
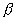
где и — некоторые числа, не равные одновременно нулю. Гиперболический параболоид

также имеет две системы прямолинейных образующих, которые определяются уравнениями

, ;

, .

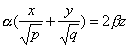
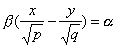
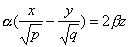
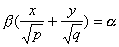
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).