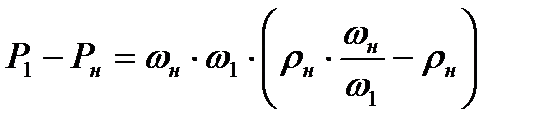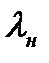Уравнение прандтля для прямого скачка

Прямой скачок уплотнения

Рассмотрим случай, когда фронт сильной волны состав­ляет прямой угол с направлением движения газа. Такая волна называется прямой ударной или прямым скачком уплотнения (рис. 8.2)

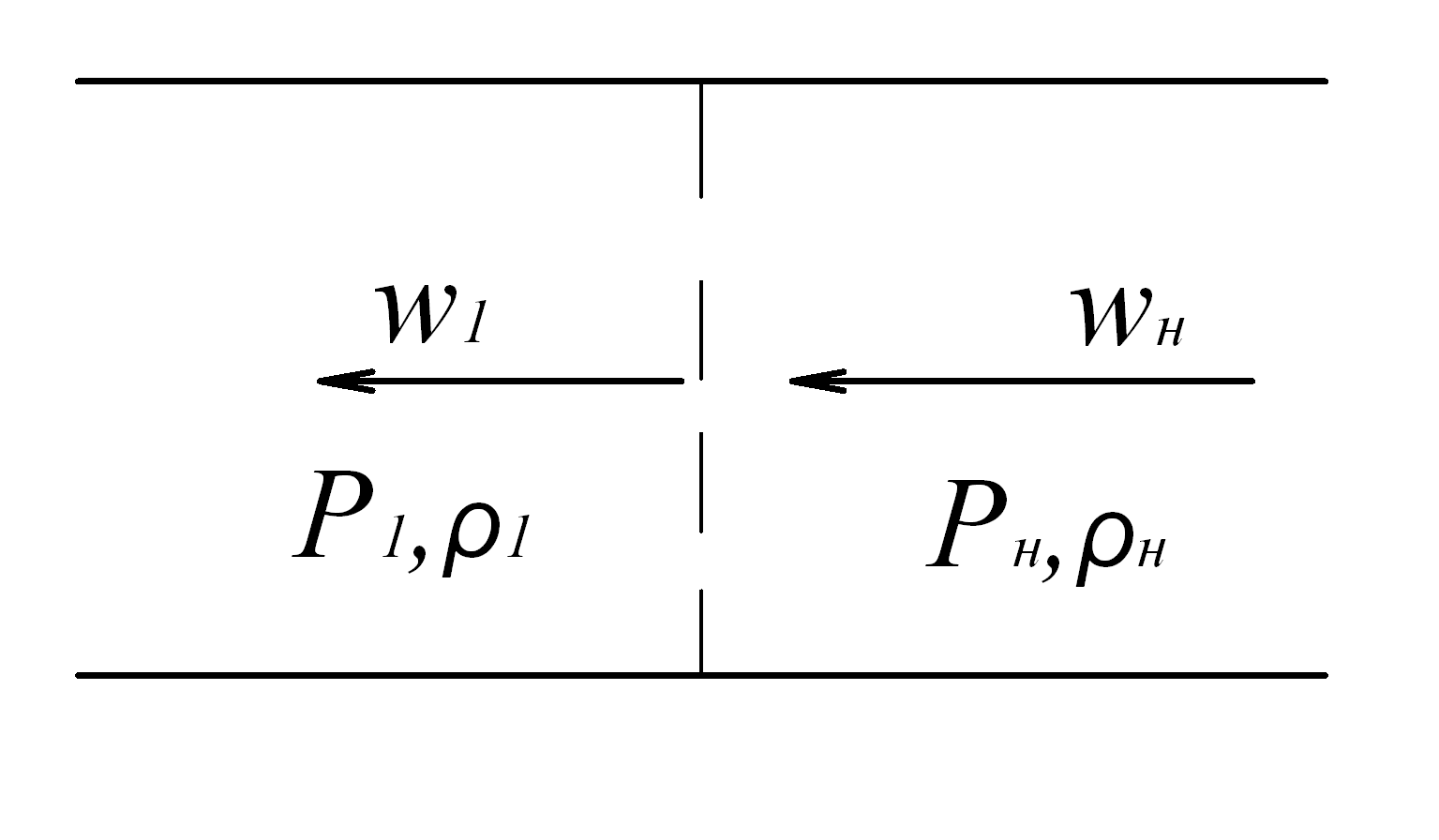
Рис. 8.2. Схема прямого скачка уплотнения

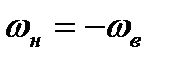
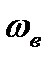
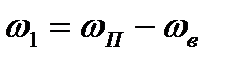
Найдем соотношения, связывающие параметры состояния газа перед и за фронтом ударной волны. Рассмотрим схему, когда фронт волны неподвижен. Если же в действительности ударная волна движется, то можно перейти к рассмотрению указанной схемы путем обращения движения. Т.е. остановим фронт волны, направив поток газа навстречу волне со скоро­стью, равной скорости распространения волны . Это равносильно тому, что вводится в рассмотрение система координат, жестко связанная с ударной волной, т.е. система координат движется со скоростью . Тогда газ будет пе­ремещаться относительно этой системы координат со скоростью перед фронтом волны и за фронтом волны со скоростью

(8.6)

Таким образом, в выбранной системе координат имеется неподвижная поверхность (ударная волна), которую пересе­кает газ. При этом параметры потока таза: скорость движения, плотность, давление и температура — претерпевает скачкооб­разное изменение. Именно поэтому ударную волну называют еще скачком уплотнения.

Визуально скачки уплотнения можно наблюдать в сверхзвуковых аэродинамических трубах при обтекании воздухом не­подвижных твердых тел.

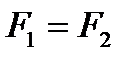
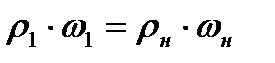
Для отыскания связи параметров потока по обе стороны скачка уплотнения воспользуемся уравнением неразрывности, которое для случая принимает вид

(8.7)

и уравнением изменения количества движения

(8.8)

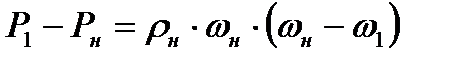
Равенство (8.8) можно преобразовать

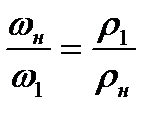
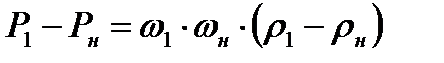
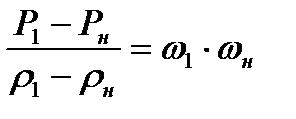
Подставляя сюда выражение , найденное из (8.7), получим

(8.9)

(8.10)

Найдем соотношение, связывающее скорость газа по обе стороны скачка уплотнения со скоростью звука. Для этого вос­пользуемся уравнением Бернулли-Сен-Венана для двух сечений, расположенных на бесконечно близком расстоянии друг от дру­га: одно сечение выбрано но одну сторону скачка уплотнения (в невозмущенной области), другое — за скачком уплотнения

(8.11)

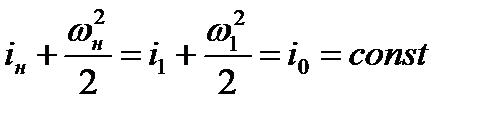
Правомерность использования этого уравнения вытекает из того, что боковая поверхность отсека потока 1-Н (т.е. в области скачка) ничтожна мала, энергообменом через эту по­верхность можно пренебречь.

Согласно (1.18) можно записать

(8.12)

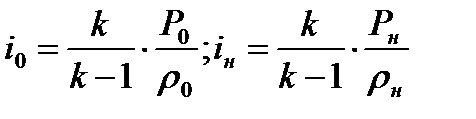
Подставляя эти значения энтальпии в (8.11) и решая уравнение относительно 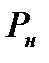, получим

(8.13)

По аналогии из (8.11), с учетом (8.12), можно по­лучить равенство

(8.14)

Вычитая почленно равенство (8.13) из (8.14), имеем

(8.15)

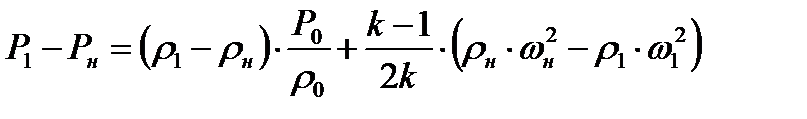
Используя соотношение (8.7), преобразуем равенство (8.8) к виду

(8.16)

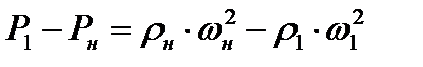
Подставляя (8.16) в (8.15), после несложных выкла­док можно получить

(8.17)

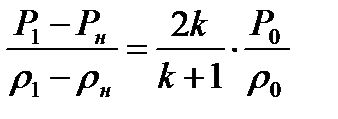
Воспользуемся выражением (3.10), которое с учетом уравнения Клапейрона-Менделеева (1.3) примет вид

(8.18)

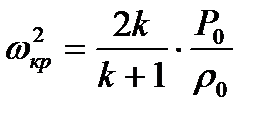
Используя последнее равенство, могло выражение (8.17) представить к виду

(8.19)

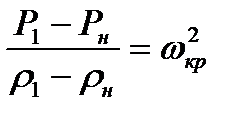
Сопоставляя равенства (8.10) и (8.19), можно по­лучить искомое соотношение, связывающее скорости потока га­за перед и за скачком уплотнения с критической скоростью.

(8.20)

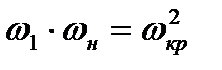
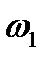
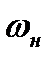
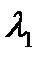
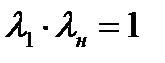
Последнее соотношение называется формулой Прандтля. Его можно представить еще иначе, если заменить в нем ско­рости и через соответствующие значения коэффициента скорости и

(8.21)

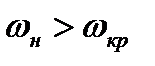
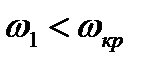
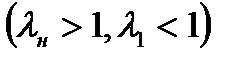
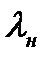
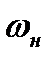
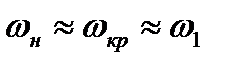
Соотношения (8.20) и (8.21) позволяют сделать важ­ный вывод. В прямом скачке уплотнения всегда сверхзвуковая скорость газа переходит в дозвуковую, так как если , то . Более того, чем выше значение безразмерной скорости (следовательно и ), тем меньше ее значение после скачка. Иными словами, чем вы­ше начальная скорость сверхзвукового потока, тем сильнее получается скачок уплотнения. С уменьшением начальной ско­рости скачок ослабевает и исчезает совсем, при Тем самым доказывается, что ударные волны возможны только при сверхзвуковых течениях газа. Этот вывод подтверждается и экспериментально.

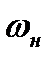
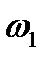
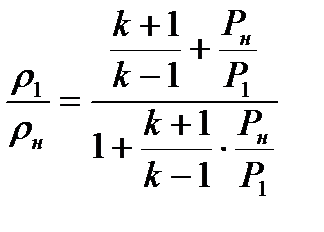
Установим теперь связь между давлением и плотностью газа в скачке уплотнения. Для этого используя выражение (8.13) и (8.14) и исключая из них скорости и , с учетом (8.9) можно получить (выкладки опускаются)

(8.22)

Соотношение (8.22) позволяет судить о термодинами­ческом процессе изменения состояния газа в скачке уплотне­ния и называется ударной адиабатой или адиабатой Гюгонио.

Следует подчеркнуть, что при прохождении газа через скачок уплотнения уравнение адиабаты Пуассона (1.21) те­ряет силу, т.е. процесс движения газа становится неизоэн- тропийным. Вместо (1.21) должно использоваться уравнение ударной адиабаты (8.22).

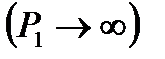
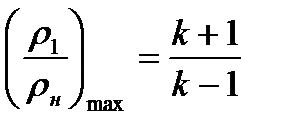
Из (8.22) видно, что при неограниченном возрастании давления в скачке уплотнения увеличение плотно­сти имеет определенный предел

(8.23)

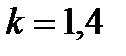
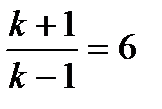
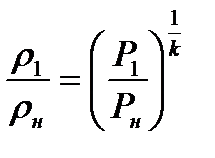
Например, для воздуха ( ) увеличение плотности в скачке уплотнения может быть не более чем в 6 раз ( ). Если бы процесс оставался адиабатическим (при прохождении скачка уплотнения), то увеличение плотно­сти с ростом давления было бы неограниченным. Это следует из выражения

(8.24)

которое получается при формальном использовании уравнения (1.21).

Графическое представление зависимостей (8.22) и (8.24) дается на рис. 8.3

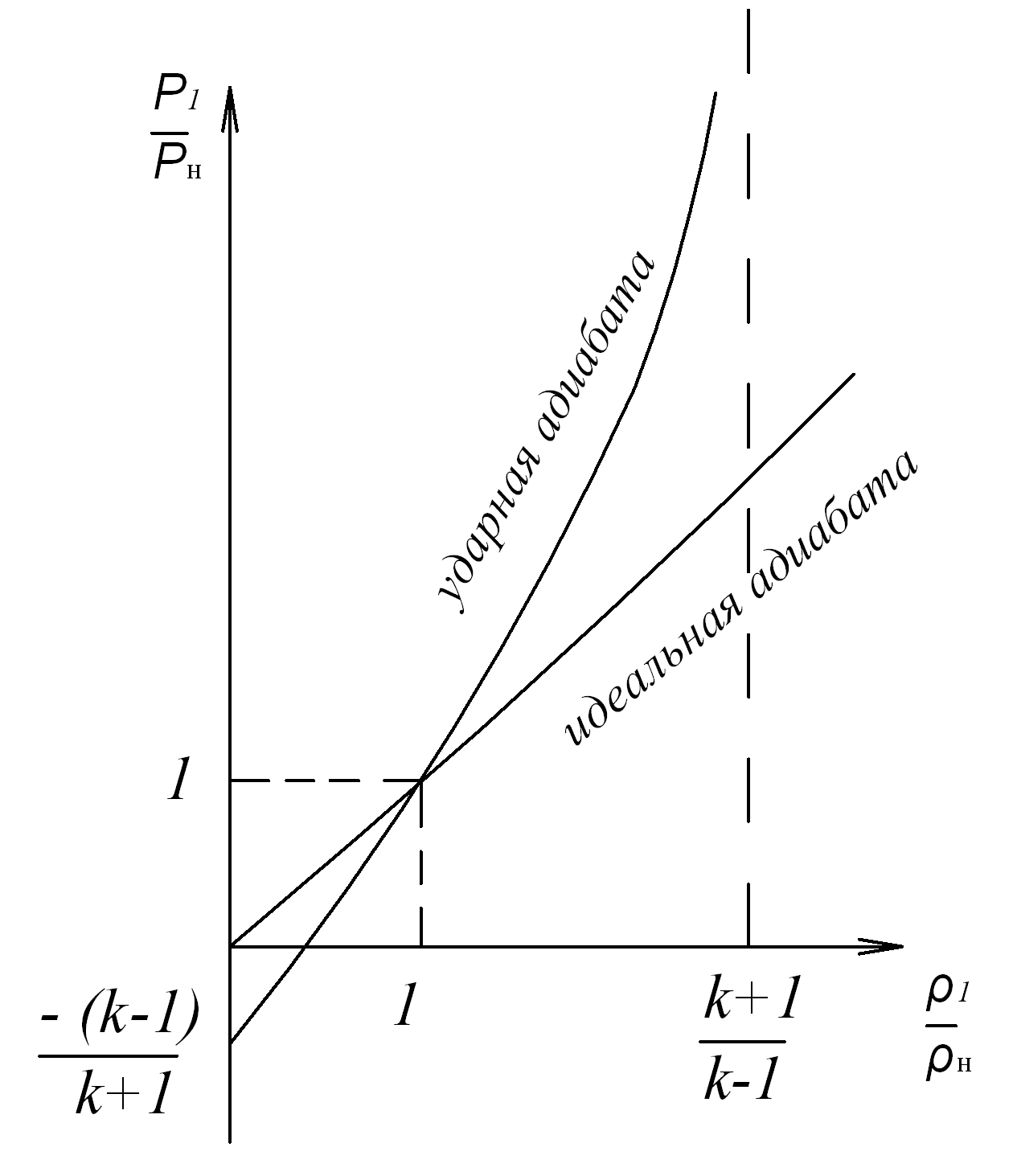
Рис. 8.3. Графическое представ­ление ударной (Гюгонио) и идеальной (Пуассона) адиабат

Выражение (8.22) иногда удобнее использовать в другом

(8.25)

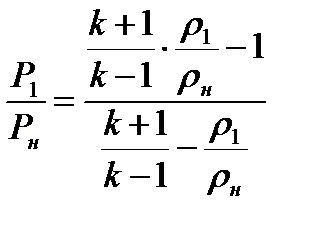
Можно выразить отношение давлений в прямом скачке уп­лотнения и в функции коэффициента скорости перед скачком уплотнения

(8.26)

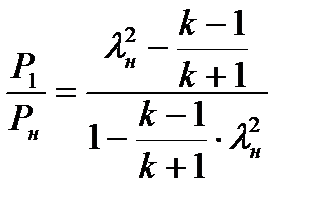
которое получается из (8.25) исключением плотности.

Выражения (8.25) и (8.26) позволяют определять потери полного давления в прямом скачке уплотнения.

Математические модели в аэрогидромеханике (стр. 6 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6

Тогда вышеперечисленные уравнения в интегральной форме запишутся следующим образом:

1) уравнение неразрывности:

, так как ; (3.1)

2) уравнение движения в форме Эйлера

; (3.2)

3) уравнение энергии

. (3.3)

Все эти уравнения содержат под знаком интеграла дифференциальные соотношения, которые надо устранить. Применяя ко всем уравнениям теорему Остроградского-Гаусса, получим:

1) , (3.4)

2) , (3.5)

3) . (3.6)

Рассмотрим одномерное течение газа и будем считать, что в сечениях 1 (до поверхности разрыва) и 2 (после поверхности разрыва) поля скоростей и других величин однородны. В этих условиях закон сохранения массы при прохождении через скачок уплотнения (уравнение неразрывности) запишется в виде:

. (3.7)

Здесь для внутренней задачи (течения газа в цилиндрической трубе) принято S1=S2, а для внешней задачи S опускается.

Уравнение движения при приведенных выше условиях дает второе искомое равенство – сохранение полного импульса (p+ru2) при прохождении через скачок уплотнения:

p1+r1u12 = p2+r2u22 (3.8)

Уравнение энергии преобразуется следующим образом:

(3.9)

(здесь заменили u=cvT).

Произведя замену , получим:

(3.10)

(здесь энтальпия h=CpT, а из уравнения Клапейрона ).

Тогда при наших допущениях получим:

. (3.11)

Учитывая, что , получим искомое третье уравнение:

. (3.12)

Это равенство представляет собой закон сохранения полной энтальпии газа при его прохождении прямо через скачок уплотнения.

С учетом уравнения Клапейрона:

(здесь , где — соотношение Майера, ).

Аналогично .

И тогда третье равенство можно записать в следующем виде:

. (3.13)

Таким образом, получили систему из трех уравнений: неразрывности течения (3.7), изменения количества движения одномерного потока (3,8) и уравнения энергии (3.13) — с тремя неизвестными величинами u2, p2, r2.

Мы видим, что независимо от характера движения (разрывного или нет) количество уравнений одно и то же. Но есть положительный мо­мент: эти соотношения в интегральном виде можно непосредственно использовать для анализа физики явления разрывного процесса. Например, уравнения (3.8) и (3.13) дают новое уравнение процесса для сплошной среды. Причем адиабата Пуассона p/rg=const, пригодная для сплошной среды (при изоэнтропическом расширении, т. е. при постоянной энтропии), теряет смысл при разрывных процессах (сверхзвуковых про­цессах при наличии скачка уплотнения). Гюгонио первый обратил на это внимание и получил адиабату при разрыве сплошности среды (при возрас­тании энтропии), названную ударной адиабатой Гюгонио. Итак, получили исходные уравнения для разрывного течения:

неразрывности ;

импульсов p1+r1u12 = p2+r2u22 ;

энергии .

Эти уравнения положены в основу теории скачка уплотнения.

3.3. Ударная адиабата Гюгонио для разрывных течений

Обратим внимание на две особенности разрывных течений:

1) в условиях неразрывного течения существует изоэнтропическая адиабата Пуассона p/rk=const. Но она недействительна для разрывных течений. Ударная адиабата Гюгонио лежит выше изоэнтропической адиабаты Пуассона, что означает возрастание энтропии при появлении разрывного течения. За счет роста энтропии появляется волновое сопротивление. Парадокс Даламбера при этом теряет смысл, так как появляется волновое сопротивление, и картина сверхзвукового обтекания тела имеет другой вид по сравнению с дозвуковым;

2) при неразрывном течении уравнение энергии и уравнение состояния приводят к уравнению процесса. Для разрывных течений этого не получается.

Выведем уравнение ударной адиабаты из уравнения импульсов

p2-p1=r1u12 — r2u22 = r1u1(u1-u2), (3.14)

так как r1u1 = r2u2.

Умножим обе части уравнения (3.14) на и получим:

.

Поскольку (т. к. u2/u1=r1/r2), то

. (3.15)

Уравнение энергии перепишем в виде:

. (3.16)

Объединим два последних уравнения в одно. Преобразуем для этого уравнение (3.16) к виду

.

Уравнение импульсов (3.15) оставим без изменений.

Приравняем левые части обоих уравнений, т. е.

(3.17)

Сгруппировав члены с р1 и р2, получим:

;

. (3.18)

Умножив обе части равенства (3.18) на (-1/r1), получим:

.

Тогда .

. (3.19)

Это и есть уравнение ударной адиабаты Гюгонио.

Итак, интегралы уравнений разрывного одномерного течения после преобразований дают отличное от изоэнтропической адиабаты Пуассона выражение. Как только переходят к разрывному течению, то получают ударную адиабату Гюгонио.

Построим графики сравнения двух адиабат: изоэнтропической и ударной.

Ударная адиабата за исключением небольшой области лежит выше адиабаты Пуассона. График для газа с k=1,4 выглядит следующим об­разом (рис. 23):

В отличие от непрерывного движения сплошной среды с плавным изме­нением параметров вдоль направления распространения потока разрывное движение характеризуется конечным скачком параметров газа в некотором сечении. Отсюда можно сделать заключение, что прохождение идеального газа сквозь скачок уплотнения не является изоэнтропическим процессом, а сопровождается необратимым переходом механической энергии в тепловую.

В физическом отношении это означает, что при прохождении через скачок уплотнения энтропия возрастает:

, (3.20)

где S1 – энтропия до скачка, S2- энтропия после скачка.

.

В силу уравнения Пуассона ( p/rk =const ) первые два члена составляют 1 и тогда

. (3.21)

Так как p2>p2из (см. рис. 23), следовательно S2>S1 при разрыве сплошности. Отсюда следует, что в природе существует только прямой скачок уплотнения, а прямого скачка разрежения не существует, поскольку в этом случае энтропия будет убывать, а это невозможно в силу второго закона термодинамики (энтропия может либо оставаться постоянной, либо возрастать — третьего не дано).

Таким образом, волновое сопротивление, появляющееся при сверхзвуковом обтекании, характеризуется возрастанием энтропии.

3.4. Уравнение Прандтля для прямого скачка уплотнения

Получим необходимое для вывода соотношение из интегралов основных уравнений для скачка уплотнения. Возьмем уравнение сохранения полного импульса (3.I4): p2-p1=r1u12 — r2u22 или

(из закона сохранения массы: r1u1 =r2u2).

Из интеграла Бернулли уравнения энергии следует, что перед скачком уплотнения имеет место следующее выражение:

. (3.22)

Оно получается следующим образом.

Уравнение энергии записывается в виде:

,

где ,

так как .

Тогда уравнение энергии будет иметь вид:

.

Константу найдем из условия a=a* при u=a* для критического течения,

тогда .

Подставляя в уравнение энергии, получим

.

Отсюда энтальпия потока перед скачком уплотнения равна

, т. к. .

За скачком уплотнения имеем:

. (3.23)

Выразив из уравнений (3.22) и (3.23) отношения p1/r1 и p2/r2 и подставив их в уравнение количеств движения , получим после преобразований:

. (3.24)

Продемонстрируем этот вывод:

;.

Подставив в уравнение количеств движения, получим:

.

Перенесем все члены в правую часть уравнения и сгруппируем:

,

тогда ,

и окончательно .

Так как u1>u2, т. е. скорость перед скачком намного больше скорости после скачка, то >0 и приходим к следующему уравнению:

или u1u2 = a*2. (3.25)

Это и есть уравнение Прандтля. Оно указывает на то, что если до скачка u1>a*, то после скачка u2

При прямом скачке уплотнения обязателен переход от сверхзвукового течения к дозвуковому, что сопровождается максимальным ростом энтропии.

При косом скачке уплотнения сверхзвуковое обтекание может остаться тоже сверхзвуковым, но меньшей интенсивности.

Уравнение Прандтля при помощи скоростного коэффициента Чаплыгина можно записать следующим образом:

l1l2=1, где ; , (3.26)

а так как , то уравнение Прандтля можно получить и в следующем виде:

. (3.27)

Отсюда . (3.28)

На этом соотношении можно построить аналог сверхзвуковой трубы. Если скорость набегающего потока на тело M1®¥, то

.

Следовательно, если создать аэрогазодинамическую трубу со скоростью M=0.4»120 м/с, то смоделируем сверхзвуковую трубу для исследования течения газа за прямым скачком уплотнения.

Теперь ответим на вопрос: какие параметры потока остаются постоянными при прохождении через прямой скачок уплотнения?

Из уравнения энергии:

, ,

где CpT1 – энтальпия набегающего потока; CpT2 — энтальпия после скачка уплотнения; h1,0 и h2,0 – полная энтальпия. Согласно закону сохранения энергии h1,0 = h2,0 = h0 или T1,0 = T2,0 = T0 (если Cp = const). Тогда а1,0=а2,0=а0; , и, следовательно, .

Итак, при прохождении через прямой скачок уплотнения энтальпия и температура адиабатически заторможенного потока сохраняют постоянную величину. Также сохраняют постоянную величину скорости звука, критические скорости до и после прямого скачка уплотнения. Кроме того, согласно формуле Клапейрона:

или .

3.5. Изменение характерных параметров газа

при прямом скачке уплотнения

За относительное изменение параметров при прямом скачке уплотнения принимается:

; ; .

Все эти величины легко находятся при использовании полученных интегралов для нашей задачи.

1. Действительно, из закона сохранения полного импульса:

.

Из уравнения сохранения масс: , тогда и, следовательно, . (3.29)

Так как из формулы Прандтля u1u2=a*2, то .

Поскольку , то , и тогда

. (3.30)

Применяя формулы перехода от l1 к М1 и наоборот, т. е.

, ,

получим искомые соотношения:

а) ;

б) ; (3.31)

в) ; г) .

2.

Применяя к этому уравнению уравнение неразрывности , получим: .

Тогда ; или (3.32)

3. .

Из закона сохранения полной энтальпии получим:

и h1=CpT1.

Тогда . (3.33)

Умножим и разделим член перед скобкой уравнения (3.33) на kR, а член на u12; .

, (3.34)

т. к. .

Если взять , то можно после преобразований написать это выражение через М1:

. (3.35)

Если взять выражение , то

. (3.36)

И наконец , т. е. температура T2 за скачком уплотнения всегда больше температуры Т1 до прямого скачка уплотнения (за счет необратимого превращения механической энергии в тепловую).

Тогда (3.37)

или . (3.38)

Как известно, при наличии необратимых потерь в адиабатической системе возрастает ее энтропия. Для определения этого возрастания воспользуемся следующей формулой:

. (3.39)

Применим это равенство к параметрам адиабатически и изоэнтропически заторможенного газа, что допустимо, т. к. изэнтропическое торможение не влияет на приращение энтропии.

(3.40)

Но из формулы Клапейрона следует: r1,0/r2,0 = p1,0/p2,0 , (3.41)

тогда . (3.42)

Эта формула выражает асимптотический закон роста энтропии при прохождении газа через скачки большой интенсивности. При сравнительно малой интенсивности скачков уплотнения, т. е. при М, близком к 1, будет наблюдаться слабое изменение энтропии, т. е. около-звуковые явления можно с достаточной степенью приближения рассматривать как изоэнтропические.

3.6. Математическая модель косого скачка уплотнения

Элементарную теорию косого скачка уплотнения можно рассматривать на примере течения газового потока внутри тупого угла. При течении внутри тупого угла сверхзвукового потока газа со скоростью u1 создается косой скачок уплотнения, который образует с горизонталь­ной осью угол b (рис. 24). Надо отме­тить, что если при прямом скач­ке уплотнения согласно теореме Прандтля сверхзвуковое течение после скачка уплотнения непре­менно становится дозвуковым, то при прохождении потока через косой скачок уплотнения сверх­звуковая скорость может сохра­ниться и за скачком уплотнения.

Разложим вектор скорости на две составляющие: нормальную u1n (перпендикулярную линии скачка уплотнения) и касательную u1t (параллельную ли­нии скачка уплотнения). При прохождении потока через косой скачок уплотнения вектор скорости потока имеет направление, параллель­ное ограничивающей поверхности. Разложим вектор скорости также на две составляющие: u2n и u2t (см. рис. 24).

При исследовании косого скачка уплотнения будем использовать сле­дующие интегральные соотношения:

1) уравнение неразрывности (закон сохранения массы), записанное для нормальных составляющих скоростей, полученных при косом скачке уплотнения:

; (3.43)

2) закон сохранения полного импульса в проекции на линию разры­ва (импульса, связанного с касательной скоростью, которая направлена по косому скачку уплотнения):

. (3.44)

То же в проекции на нормаль к линии разрыва (или теорема об изменении импульсов для нормальных составляющих скоростей):

; (3.45)

3) уравнение энергии (закон сохранения полной энтальпии):

. (3.46)

Из уравнения (3.43) с учетом (3.44) следует, что

. (3.47)

Это равенство указывает на то, что касательные составляющие скоростей до и после косого скачка уплотнения одинаковы. Иными словами, косой скачок уплотнения не вызывает изменения характера течения касательных скоростей до и после скачка уплотнения.

Тогда система уравнений (интегральных соотношений) будет иметь вид:

Видно, что полученная система уравнений для косого скачка уплотнения отличается от системы уравнений, характеризующих прямой скачок уплот­нения. Система уравнений для косого скачка уплотнения получается из системы уравнений для прямого скачка уплотнения заменой векторов ско­ростей и на их нормальные составляющие u1n и u2n. Следовательно, все, что было сказано относительно прямого скачка уп­лотнения, сохраняет свой смысл и для косого скачка уплотнения, если во всех соотношениях, полученных для прямого скачка уплотнения, заме­нить векторы скоростей и на их нормальные составляющие.

Тогда уравнение Прандтля для косого скачка уплотнения будет выглядеть следующим образом:

, (3.48)

. (3.49)

Это значение для получается из рассмотрения уравнения интегра­ла энергии в следующем виде:

.

Для нашего случая:

. (3.50)

. (3.51)

При наличии косого скачка уплотнения критическая скорость оказывается несколько меньшей, чем при прямом скачке уплотнения ().

Теорему Прандтля можно также записать в виде:

, (3.52)

где , . (3.53)

Относительное изменение характерных параметров при косом скачке уплотнения можно получить из аналогичных соотношений для прямого скачка уплотнения, если вместо векторов скоростей и в выражениях для М и l поставить их нормальные компоненты:

1) Например , (3.54)

где . Из треугольника скоростей u1n=u1sinb, тогда , и окончательно:

. (3.55)

Это же выражение через l1 выглядит следующим образом:

. (3.56)

Из треугольника скоростей: u1t=u1cos b, тогда с учетом (3.49):

Из уравнения (3.53):

. (3.57)

Следовательно, с учетом формул (3.56) и (3.57) имеем:

=

.

. (3.58)

(3.59)

. (3.60)

3)

. (3.61)

И, наконец, останутся теми же самыми, что и для прямого скачка уплотнения, выражения: h1,0= h2,0=h0; T1,0= T2,0=T0; a1,0= a2,0=a0, T1*= T2*=T* и a1*= a2*=a*.

Останется той же и ударная адиабата Гюгонио.

Из треугольников скоростей перед и за косым скачком уплотнения (рис. 24) следует:

; ,

где q — половинный угол клина, он же – угол отклонения потока за скачком; b — угол, образованный линией косого скачка уплотнения с направлением набегающего потока (вектора скорости )

u1t = u2t = u1cosb = u2cos(b-q) = u1.

Для проекций скоростей на оси прямоугольной декартовой системы координат имеем:

u1x = u1, u1y =0; u2x = u2cos(b-q), u2y = u2sin(b-q).

Еще: u1n = u1x sin b; u2n = u2x sin b — u2ycos b;

u1t = u2t = ut = u1xcosb = u2xcos b +u2ysin b =u1cos b.

Из последнего соотношения находим:

u2ysin b =(u1-u2x)cos b Þ

а) ;

б) .

С учетом предыдущих соотношений: .

Эти соотношения позволяют найти выражение касательных и нормальных компонент векторов скоростей и через их декартовые проекции:

;

;

.

Используем формулу Прандтля для косого скачка уплотнения в виде:

.

Подставим туда выражения для u1n и u2n через декартовы проекции векторов скоростей и после преобразований получим:

. (3.62)

Деля обе части этого равенства на а*2 или на , перепишем его в следующих видах:

, (3.63)

. (3.64)

Эти соотношения представляют собой уравнения семейства кривых соответственно в плоскостях (u2x/a*; u2y/a*) или (u2x/a1; u2y/a1) с параметрами l1 и M1. Полученные семейства представляют собой геометрические места точек концов вектора скорости за косым скачком уплотнения, отнесенного в первом случае к a* и во втором — к a1, причем в качестве параметров семейств используется величина скорости до скачка, отнесенная к a* или a1. Кривые этих семейств представляют собой строфоиды (их еще называют гипоциссоидами или декартовыми листами).

На рис. 25 в размерных коор­динатах (u2x; u2y) по­казана одна из таких строфоид. Она имеет асимптоту, опреде­ляемую следующим выражением:

. (3.65)

Вертикальная составляющая скорости u2 обращается в нуль (u2y=0) в двух случаях:

1) в точке B, в которой

При этом величина и направление скорости не меняются, т. е. ска­чок уплотнения вырождается в слабую волну возмущения;

2) в точке A, в которой u2x = u2 = a*2/u1 или u1 u2 = a*2 (уравнение Прандтля для прямого скачка уплотнения).

В этом случае скорость u2 имеет минимальное значение при за­данной сверхзвуковой скорости u1, следовательно, скачок уплотне­ния имеет в точке A наибольшую интенсивность.

Луч, проведенный из начала координат под углом q, равным пово­роту потока (или углу полураствора клина), пересекает строфоиду в трех точках 1, 2, 3 и, таким образом, определяет три значения вектора скорости за косым скачком уплотнения. Какие же из этих трех то­чек имеют физический смысл?

Поскольку скорость в точке 3 больше скорости в точке B (см. рис. 25), т. е. скорость u2 в этой точке больше u1, что является невозможным, т. к. за косым скачком уплотнения происходит торможение потока (наличие скорости u2>u2 свидетельствует о существовании скачка разрежения, что в термодинамическом отношении не имеет места из-за уменьшения энтропии, а это невозможно). Поэтому точка 3 и вообще обе бесконечные ветви строфоиды, расположенные вправо от точки В и уходящие к асимптоте, являются нерабочими. Следовательно, рабочими точками, имеющими физический смысл, могут быть только точки 1 и 2.

При определенных углах обтекания клина или сверхзвукового течения внутри тупого угла за косыми скачками уплотнения может наблюдаться и сверхзвуковое течение, следовательно, интенсивность косого скачка уплотнения всегда меньше прямого скачка уплотнения, поскольку после прямого скачка уплотнения скорость потока всегда дозвуковая.

Так как точка 3 противоречит второму закону термодинамики (не реализуется), то ударную поляру часто изображают так (рис. 26):

Такая диаграмма в координатах (u2x/a*; u2y/a*) позволяет весь­ма просто найти все основные величины:ut, u1n, u2n и угол b, характеризующий косой скачок уплотнения. Для этого из начала координат (см. рис. 27) под углом q (угол полураствора клина, или угол откло­нения потока за скачком уплотнения) проводят прямую линию до пересече­ния с полярой (например, точка E). Затем из точки B через точ­ку E проводят прямую линию и к ней из начала координат восстанавли­вают перпендикуляр (линия OG). Тогда угол GOB=b, а отрезок JG представляет собой касательную составляющую ut скоростей и (т. к. ut = u1cosb или OG=OBcosb), деленную на a*. Отрезок GE представляет собой нормальную составляющую u2n скорости (u2n = u2sin(b-q) или GE=OEsin(b-q), деленную на a*. Отрезок BG представляет собой нормальную составляющую u1n скорости (u1n=u1sinb или BG=OBsinb), деленную на a*. Аналогично можно найти параметры потока по этой диаграмме и для точки D, также характеризующей отношение u2/a*, но для другого возможного направления косого скачка уплотнения b’ (причем b’>b). Пос­кольку в точке D скорость меньше скорости в точке E (при одной и той же скорости ), то, следовательно, точке D со­ответствует косой скачок большей интенсивности, или по-другому, большим углам со­ответствуют косые скачки уп­лотнения большей интенсивнос­ти.

По условию набегающий поток является сверхзвуковым, следовательно, отрезок OB=u1/a*>1. С другой стороны, из уравнения (3.62) легко заключить, что точка A пересечения строфоиды с осью u2x/a* (т. е. при u2y=0) будет иметь абсциссу (т. к. u1>a*, поток сверхзвуковой). Отсюда следует, что на оси u2x/a* между точ­ками A и B будет находиться точка S, соответствующая крити­ческой скорости, т. е. отрезок OS=1 (причем в этой точке выпол­няется условие инверсии OA×OB=OS2). Окружность радиуса OS=1 разграничивает области до — и сверхзвуковых течений (u2/a* 1) . Другими словами, окружность радиуса OS=1 очерчивает на строфоиде области, где скорости u2 за косым скачком уплотнения могут быть дозвуковыми (u2/a* 1). Отметим также, что существует такое значение угла q=qmax, при котором точки D и E сольются в одну, и ей будет отвечать лишь одно значение угла b и лишь одно расположение косого скачка уплот­нения. Это будет предельный случай так называемого присоединенного скачка уплотнения (рис. 28, а).

Если же q>qmax, то образуется отсоединенный криволинейный скачок уплотнения (рис. 28, б), расчет которого является более сложной задачей, чем было изложено выше. Элементарная теория косого скачка уплотнения действительна лишь при обтекании клина или течения внутри тупого угла до таких углов qmax, при которых скачок уплотнения является присоединенным. Следовательно, нужно всегда сверять по удар­ной поляре заданный угол q с углом qmax, так как все приведен­ные соотношения справедливы лишь для углов q qmax (этот случай бывает только для неудобообтекаемых тел (рис.29), но такие контуры стараются не делать). Определим связь между угла­ми b и q при заданном числе M1 набегающего потока. С этой целью воспользуемся соотношением Прандтля для косого скачка уплотнения: . Учитывая, что u1n=u1sinb, , получим:

,

поскольку , откуда .

Тогда: . (3.66)

Из соотношения (3.66) получается зависимость между углами b, q и скоростным коэффициентом l1.

Разделим обе части этого равенства на a*2:

,

. (3.67)

Заменяя в уравнении (3.67) l1 на число Маха М1 по формуле

,

,

,

. (3.68)

Разрешая равенство (3.68) относительно tgq, получим:

. (3.69)

Как было ранее отмечено, каждому заданному значению q qmax (AC – отсоединенный скачок уплотнения). Выясним условия, при которых поток за косым скачком уплотнения будет до — ­или сверхзвуковым. Для этого воспользуемся формулой (3.28) зависимости числа Маха M2 за скачком от числа M1 до скачка для прямого скачка уплотнения и произведем замену в этой фор­муле M1 на M1sinb и M2 на M2sin(b-q), справедливых для косого скачка уплотнения. Тогда получаем искомую формулу связи:

. (3.71)

Пользуясь этим выражением и соотношением

, (3.72)

можно выразить число Маха за косым скачком уплотнения M2 через чис­ло M1 до скачка и угол b. При этом при одном и том же M1 двум различным значениям b, соответствующим сильному и слабому скачкам, будут отвечать два отличных друг от друга значения M2, причем сильный скачок уплотнения, подобно прямому, переводит сверхзву­ковой поток в дозвуковой, а слабый скачок почти всегда сохраняет по­ток сверхзвуковым.

Если q>qmax, то, как указывалось, наличие прямолинейного присоединенного к вершине угла (клина) 0 косого скачка уплотнения невозможно. Вверх по течению перед точкой 0 возникает криволинейная «головная» ударная волна или отсоединенный скачок уплотнения АС (рис. 30). В непосредственной близости к точке А отсоединенный скачок АС ведет себя как прямой, а при удалении от точки А сначала как сильный косой скачок, а затем с уменьшением местного уг­ла b постепенно ослабевает и переходит в прямолинейный косой ска­чок. При этом за отсоединенным скачком уплотнения имеет место как до-, так и сверхзвуковое течение газа. За участком АВ образуется дозвуковая зона течения, за участком ВС – сверхзвуковая. Эти две зоны потока за скачком разделяются линией ВD, вдоль которой скорость газа равна местной скорости звука.

1. Механика жидкости и газа. М.: Наука,19с.

2. Механика сплошной среды. Т. II. М.: Наука,19с.

3. , Механика сплошных сред. М.: Гостехтеоретиздат, 19с.

4. Седов Л. И. Плоские задачи гидродинамики и аэродинамики. М.: Наука, 19с.

5. Гидромеханика. М.: Изд-во иностранной литературы, 19с.

6. Прикладная газовая динамика. Ч. I, II. М.: Наука, 19с., 304 с.

7. Лекции по основам газовой динамики. М.: Наука, 19с.

8. Аэрогидромеханика разрывных течений идеального газа: Учебное пособие. Самара: Изд-во СамГУ, 19с.

9. Механика сплошных сред в задачах. Т.1,2 / Под ред. . М.: Московский Лицей, 1996, 396 с., 394 с.

1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В АЭРОДИНАМИКЕ …….

1.1. Математическая модель плоского движения

идеальной несжимаемой жидкости. …………………….

1.2. Комплексные потенциалы и характеризуемые ими

1.3. Математическая модель бесциркуляционного

обтекания кругового цилиндра идеальной жидкостью..

1.4. Математическая модель циркуляционного

обтекания кругового цилиндра идеальной жидкостью..

1.5. Теорема Жуковского о подъёмной силе крыла …………

1.6. Математическая модель обтекания крылового

профиля по методу конформных отображений …………

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ГАЗОВОЙ ДИНАМИКЕ..

2.1. Изоэнтропийные соотношения для идеального газа …..

2.2. Математическая модель движения газа по соплу Лаваля

2.3. Распространение малых возмущений

в потоке сжимаемого газа ………………………………….

2.4. Математическая модель плоского безвихревого

движения идеального сжимаемого газа ……………….…

2.5. Линейные преобразования Прандтля

для определения малых возмущений параметров газа …

2.6. Математическая модель дозвукового обтекания

тонкого профиля потоком идеального сжимаемого газа

2.7. Математическая модель сверхзвукового обтекания тонкого профиля потоком идеального сжимаемого газа

3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ РАЗРЫВНЫХ ТЕЧЕНИЙ..

3.1. Сильные разрывы в газе. Прямые и косые

3.2. Математическая модель прямого скачка уплотнения ….

3.3. Ударная адиабата Гюгонио для разрывных течений …..

3.4. Уравнение Прандтля для прямого скачка уплотнения.

3.5. Изменение характерных параметров газа

при прямом скачке уплотнения ………………………….

3.6. Математическая модель косого скачка уплотнения ……

Изменение параметров газа на скачке уплотнения

Тема 1.Теоретические основы аэромеханики

1.11. Изменение параметров газа на скачке уплотнения

Изменение нормальной скорости

Используя уравнение изменения количества движения (1.88), уравнение сохранения массы (1.87) и уравнение сохранения энергии (1.92) взяв в качестве const величину V 2 _пр/2 ( V_пр – предельно-возможная скорость потока, при истечении, например, в пространство, где Т=0), получим следующее соотношение нормальных скоростей

(1.94)

Предельная скорость V_пр связана с критической скоростью звука а_кр соотношением

(1.95)

Рекомендуемые файлы

(1.96)

Величину а_кр можно получить из выражения

(1.97)

Если известны только число М и угол , то можно пользоваться уравнением вида

(1.98)

Для воздуха c=1.4, поэтому

(1.99)

Отсюда следует вывод, что при неограниченном росте числа М скорость потока при переходе через скачок уплотнения уменьшается не более чем в 6 раз (при М, p/2).

Кроме того, для прямого скачка V=0 и выражение (1.96) принимает вид

(1.100)

т.е. после прямого скачка скорость потока становится дозвуковой, так как V₁>а.

Воспользовавшись уравнением сохранения массы (1.87) и соотношением нормальных скоростей (1.98) получим выражение для соотношения плотностей газа до и после скачка уплотнения

. (1.100)

Таким образом, отношение плотностей, как и нормальных скоростей, зависит только от параметра М sin.

Кроме того, можно заметить, что с ростом числа М плотность за скачком возрастает не беспредельно. Полагая Мsin= получим предел отношения плотностей

. (1.101)

Для воздуха при c=1.4 получаем ₂=6₁.

Причиной ограничения увеличения плотности является увеличение температуры при ударном сжатии. Нагрев газа препятствует его уплотнению.

Изменение давления и температуры

Воспользовавшись уравнением изменения количества движения (1.88) и соотношением нормальных скоростей (1.98) получим

(1.102)

Для определения соотношения температуры воспользуемся уравнением состояния газа до и после скачка и разделим одно из них на другое. Тогда

(1.103)

Выводы: таким образом, отношение давлений и температур на скачке зависят также от параметра М sin. При неограниченном росте этого параметра давление р₂ и температура T₂ возрастают также неограниченно, но отношение температур растет менее интенсивно за счет ограниченного роста плотности (рис.1.44). Это справедливо для газа постоянной теплоемкости.

1.12. Коэффициент восстановления полного давления

По закону сохранения энергии при переходе через скачок общий запас энергии не изменяется, т.е. энтальпия торможения до и после скачка одинакова

. (1.104)

Для газа с постоянной теплоемкостью энтальпия однозначно выражается через параметры торможения, предельную и критическую скорости

. (1.105)

Таким образом, при переходе через скачок уплотнения остаются постоянными следующие параметры торможения

, (1.106)

а также предельная и критическая скорости.

Однако полное давление за скачком и плотность будут меньше, чем до скачка ( и ), так как процесс ударного сжатия на скачке является изоэнтропическим и сопровождается потерями полного давления за счет необратимого прихода части кинетической энергии в тепло.

Эти потери полного давления на скачке характеризуются коэффициентом восстановления полного давления

(1.107)

Коэффициент n всегда меньше единицы и убывает с ростом числа М, так как при этом возрастает интенсивность скачка и необратимые потери на нем.

Можно показать, что

. (1.108)

а так как отношение давлений и плотностей зависят от параметра Msin b, то и n зависит только от этого параметра ( рис.1.45)

Выводы: анализ выражения (1.108) и его графического представления показывает, что при Msin b ®1 и n®1, а при увеличении Msin b коэффициент n уменьшается.

При одном и том же числе М чем больше угол наклона скачка b, тем меньше n. Это необходимо учитывать при выборе форм сверхзвуковых летательных аппаратов, особенно входных устройств силовых установок, в которых потери полного давления желательно свести к минимуму.

Потери полного давления необходимо также учитывать при определении скорости полета летательного аппарата (числа М) с помощью приемника воздушного давления (ПВД).

Принцип измерения числа М

Принцип измерения числа М основан на измерении отношения давления торможения к статическому давлению невозмущенного потока при помощи приемника воздушного давления (рис. 1.47).

Центральный канал ПВД является приемником полного давления, так как вход в него располагается в точке полного торможения. Отверстия на боковой поверхности являются приемниками статического давления.

На дозвуковых скоростях полета связь между числом М и указанным отношением давлений определяется формулой

(1.109)

При сверхзвуковых скоростях эта связь становится более сложной, поскольку перед ПВД образуется скачок уплотнения и на нем имеются потери полного давления. Тогда, учитывая. что в районе центрального канала угол b=p/2, получаем

, (1.110)

— давление торможения за скачком;

— полное давление перед скачком.

Данное выражение носит название формулы Релея.

Так как M=V/a , то формулы (1.109) и (1.110) используются для тарировки указателей не только числа М , но и скорости полета.

Графически зависимости (1.109) и (1.110) представлены на рис. 1.48.

Расхождение этих зависимостей при М>1 и характеризует потери полного давления на скачке.

1.13. Сверхзвуковое течение расширения

Рассмотрим сверхзвуковое плоскопараллельное течение невязкого газа около двух плоскостей А₁О и ОА₂, образующих излом в точке О с внешним углом более 180 0 (рис.1.49).

Параметры газа около плоскости А₁О будем считать исходными, невозмущенными.

Поворачиваясь в точке излома на угол w сверхзвуковой поток расширяется. При этом скорость будет возрастать, а давление, плотность и температура — уменьшаться.

Вершина угла О является источником слабых возмущений, следовательно, от нее будут исходить характеристики. Очевидно, первая характеристика будет наклонена к поверхности А₁О под углом , а последняя — к поверхности ОА₂ под углом .

Поскольку М₂>M₁, то m₂ * от угла поворота w при условии, что исходное число М=1.

Изоэнтропическое течение- течение газа с постоянной энтропией во всем поле течения.

С другой стороны, для изоэнтропического течения справедлива зависимость р₂/р * от числа М, вытекающая из уравнения сохранения энергии

. (1.111)

График этой зависимости представлен на рис.1.50 нижней кривой.

Алгоритм определения параметров по данному графику следующий:

1. По числу М₁ на нижней кривой определяем р₁/р * до поворота.

2. При этом значении переходим на верхнюю кривую и определяем угол w₁, на который нужно повернуть поток, чтобы разогнать его от М=1 до М₁.

3. Добавив к w₁ угол фактического поворота w определяем по верхней кривой отношение р₂/р * .

4. Переходя при этом значении на нижнюю кривую, определяем число М_2.

5. Остальные параметры определяются из формул

, , , V₂=M₂a_2. (1.112)

1.14. Обтекание тел сверхзвуковым потоком

Рассмотрим обтекание носовой части затупленного тела сверхзвуковым потоком (рис.1.51).

В этом случае перед телом образуется отошедшая криволинейная ударная волна. Основной особенностью течения за криволинейной отошедшей ударной волной является наличие зоны дозвукового обтекания между телом и ударной волной. Это объясняется тем, что за прямым скачком уплотнения или близким к прямому поток всегда дозвуковой. По мере удаления от линии тока, приходящей в точку полного торможения, интенсивность ударной волны становится слабее, угол ее наклона уменьшается, а скорости за ней увеличиваются. И в какой-то точке “а” ударная волна переходит в слабый скачок, за которым скорость сверхзвуковая. В дозвуковой зоне за ударной волной поток разгоняется в силу уменьшения площади поперечного сечения струек и на линии “а-а” достигает скорости звука.

С учетом рассмотренных особенностей сверхзвуковых течений около простых тел построим картину течения возле тела сложной формы (рис.1.52).

Картина обтекания головной части зависит от ее формы — затупленной, конической или клиновидной. Далее в местах, где имеет место поджатия сверхзвукового потока (вогнутые углы), образуются скачки уплотнения. В местах наличия выпуклых углов имеют место течения расширения.

За кормовой частью вследствие необходимости выравнивания потока до направления невозмущенного потока образуется угол, на котором появляется кормовой скачок уплотнения, на котором поток тормозится до скорости, примерно равной V_¥.

1.15. Волновой срыв

Существенное влияние на характер течения в пограничном слое при трансзвуковых и сверхзвуковых скоростях полета оказывают скачки уплотнения. Результатом взаимодействия скачков уплотнения и пограничного слоя может быть волновой срыв.

Волновым срывом называется обратное течение в дозвуковой части пограничного слоя, вызванное перепадом давления на скачке уплотнения.

Рассмотрим физическую природу волнового срыва. При наличии сверхзвукового потока над поверхностью тела в нижней части пограничного слоя имеется зона дозвукового течения, так как непосредственно на поверхности V=0 и достигает величины V=a на каком-то расстоянии от тела. Поэтому, если в потоке имеется скачок уплотнения, то он не доходит до поверхности (рис. 1.53) на расстояние, равное толщине дозвуковой части пограничного слоя.

В силу этого под действием повышенного давления за скачком (p₂>p₁) возникает обратное течение между основанием скачка уплотнения и поверхностью тела. Под действием перетеканий пограничный слой перед скачком набухает, в результате возникает обтекание, подобное обтеканию внутреннего тупого угла сверхзвуковым потоком с образованием вторичного скачка уплотнения. Образуется система скачков в виде буквы . Набухший слой перед скачком может оторваться, что вызывает периодичность в изменении давления. Кроме того, нестационарность течения обуславливается и тем, что при образовании лямбдаобразного скачка интенсивность основного скачка уменьшается, перетекания уменьшаются, дополнительный скачок может слиться с основным и процесс повторится. Цикличность в изменении давления приводит к росту сопротивления и может вызвать тряску элементов летательного аппарата.

Следует заметить, что при турбулентном пограничном слое — образные скачки обычно не образуются, вибрация скачка проявляется слабее, так как из-за более наполненного профиля скоростей в турбулентном пограничного слое скачок уплотнения подходит к поверхности ближе и перетекания при этом слабее.

1.16. Особенности гиперзвуковых течений

Гиперзвуковыми называются течения с большими сверхзвуковыми скоростями ( обычно при М> 4. 5), при которых в результате взаимодействия газа с обтекаемым телом начинаются происходить изменения его физико-механических свойств. Эти изменения вызывают ряд особенностей в силовом и тепловом взаимодействии газа и обтекаемого тела.

· Во — первых, с увеличением чисел М набегающего потока углы наклона скачков уплотнения уменьшаются и скачки приближаются к поверхности. Это приводит к взаимодействию скачка уплотнения и пограничного слоя. Головной скачок как бы прижимает пограничный слой к поверхности, ограничивая его толщину. С другой стороны, высокая температура за скачком уменьшает плотность газа, что способствует возрастанию толщины пограничного слоя. Это создает эффект увеличения толщины тела, что проводит к деформации головной ударной волны и увеличению давления за ней.

· Вторая особенность состоит в том, что малые изменения параметров движения тела приводят к существенным изменениям параметров газа. Это приводит к тому, что применение линейной теории начинает давать большие погрешности при определении аэродинамических характеристик.

· И третья особенность заключается в том, что из-за высоких температур за головной ударной волной и в пограничном слое вначале начинает изменять теплоемкость газа, а затем при дальнейшем росте температуры возникают диссоциация и ионизация газа, значительно влияющие на термодинамические свойства газа.

Таким образом, при гиперзвуковых скоростях становятся непригодными или ограниченно пригодными те методы исследования аэродинамических характеристик, которые применяются при умеренных сверхзвуковых скоростях.

Тем не менее и при больших числах М, рассматривая обтекание весьма тонких тел, поставленных под небольшими углами атаки к потоку, можно получить приближенные и достаточно простые методы определения аэродинамических характеристик.

Например, угол наклона скачка уплотнения определяется выражением

, (1.113)

а коэффициент давления

. (1.114)

Данные формулы дают хорошее совпадение с точными решениями при М>3.

1.17. Аэродинамический нагрев

При полете с большими сверхзвуковыми скоростями элементы поверхности летательного аппарата нагреваются и зачастую до весьма высоких температур. Например, при М=3 заостренная носовая часть фюзеляжа нагревается до 315°С, передние кромки крыльев — до 270°С и т.д.

Явление нагрева летательного аппарата движущегося в воздухе, и самого воздуха теплом, выделяемым в результате перехода кинетической энергии поступательного движения частиц в тепловую называется кинетическим (аэродинамическим) нагревом. Последствия кинетического нагрева:

— ухудшаются условия работы экипажа,

— ухудшаются условия работы радиоэлектронного оборудования,

— снижается прочность материалов конструкции,

— повышается скорость реакции коррозии,

— происходит деформация обшивки и нарушение аэродинамических форм отдельных частей летательного аппарата,

— существенно изменяются характеристики пограничного слоя, что сказывается на суммарных аэродинамических характеристиках летательного аппарата.

Для оценки влияния кинетического нагрева на аэродинамику летательного аппарата рассмотрим, как изменяются некоторые параметры потока при его нагреве.

При увеличении температуры газа плотность воздуха уменьшается, а коэффициент динамической вязкости увеличивается, что подтверждается их соотношением для двух точек одного сечения пограничного слоя

; (1.115)

Толщина пограничного слоя определяется выражениями

, , (1.116)

где и определяются по определяющей температуре.

Кинетический нагрев оказывает существенное влияние и на коэффициент трения. С увеличением температуры из-за роста числа М коэффициент С_f уменьшается за счет уменьшения плотности. Причем, в турбулентном пограничном слое коэффициент С_f с ростом числа М уменьшается более интенсивно, чем в ламинарном, из-за более интенсивного уменьшения градиента скорости с увеличением толщины пограничного слоя при кинетическом нагреве (рис. 1.54).

Для оценки способов снижения кинетического нагрева рассмотрим тепловой баланс между обшивкой и внешней средой.

В общем случае к единице площади обшивки летательного аппарата в единицу времени поступает суммарный тепловой поток , содержащий конвективный тепловой поток от воздуха , тепловой поток от земной и солнечной радиации и поток от оборудования , который может подводиться к обшивке или отводиться от нее, т.е.

=++ (1.117)

Удельные тепловые потоки за счет земной и солнечной радиации обычно невелики по сравнению с конвективным и ими пренебрегают.

Тепловой поток от оборудования обычно известен из характеристик источников тепла.

С другой стороны, удельный тепловой поток, идущий от обшивки в пространство в виде лучеиспускания, уравновешивает тепловой поток в обшивку в случае установившегося теплообмена, т.е. для оценки температуры обшивки рассматривают равенство конвективного и лучевого потоков

= (1.118)

или с учетом выражений для через температуру и в соответствии с законом Стефана-Больцмана

, (1.119)

где — коэффициент теплопередачи, C_p — удельная теплоемкость при постоянном давлении, — степень черноты обшивки, показывающая, во сколько раз излучательная способность поверхности меньше излучательной способности абсолютно черного тела, =5.67 Вт/м 2 град 4 – постоянная Стефана — Больцмана (коэффициент излучения абсолютно черного тела), — температура восстановления, причем коэффициент восстановления для ламинарного пограничного слоя равен r=0,85, а для турбулентного r=0,9.

Из анализа (1.119) следует, что для уменьшения температуры обшивки необходимо уменьшать конвективный тепловой поток и увеличивать излучательную способность поверхности.

Это можно сделать следующими способами:

— уменьшение скорости или увеличение высоты полета;

— уменьшение коэффициента трения за счет ламинаризации пограничного слоя;

— затупление головной части летательного аппарата;

— теплоизоляция (нанесение материалов с низкой теплопроводностью или с большой теплоемкостью);

— искусственное охлаждение поверхности (например, пористое охлаждение или применение сублимационных обмазок, испаряющихся с большим поглощением тепла).

Обычно уравнение (1.119) решается графически. Задаваясь рядом значений T_w строят зависимости от нее и . Точка пересечения этих кривых и дает величину равновесной радиационной температуры обшивки, при которой сбалансированы все действующие на нее тепловые потоки (рис. 1.55).

Следует заметить, что функция (T_w) изменяется при изменении режима полета, а функция (T_w) зависит от материала и состояния поверхности обшивки.