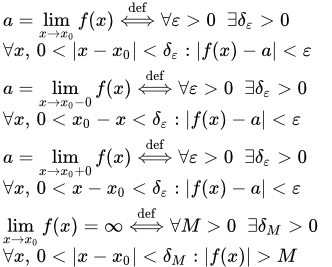Уравнение предел функции в точке

Определение предела функции в конечной точке

Определение предела функции по Коши

Конечный предел функции в конечной точке

Определение конечного предела функции по Коши
Число a называется пределом функции f ( x ) в точке x ₀ , если
1) существует такая проколотая окрестность конечной точки x ₀ , на которой функция определена;
2) для любого сколь угодно малого положительного числа ε > 0 существует такое число δ_ε > 0 , зависящее от ε , что для всех x , принадлежащих проколотой δ_ε — окрестности точки x ₀ : 0 |x – x ₀ | , значения функции принадлежат ε — окрестности точки a :
|f ( x ) – a| .
Предел функции обозначается так:
.
Или при .

С помощью логических символов существования и всеобщности определение предела функции можно записать следующим образом:
.

Односторонние пределы

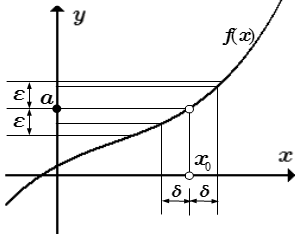
Функция может быть определена не с двух сторон от точки , а в некоторой левой окрестности точки , при или в некоторой правой окрестности, при . Также функция может иметь разрыв в точке . Тогда используют односторонние пределы.

Левый предел в точке (левосторонний предел):
.
Правый предел в точке (правосторонний предел):
.
Пределы слева и справа часто обозначают так:
; .

Бесконечный предел функции в конечной точке

Определение бесконечного предела функции по Коши
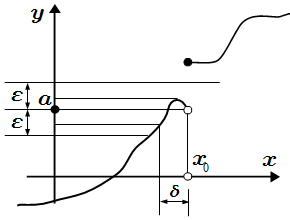
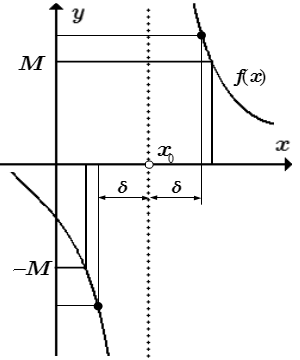
Предел функции f ( x ) при x → x ₀ равен бесконечности, если
1) существует такая проколотая окрестность конечной точки x ₀ , на которой функция определена;
2) для любого, сколь угодно большого числа M > 0 , существует такое число δ_M > 0 , зависящее от M , что для всех x , принадлежащих проколотой δ_M — окрестности точки x ₀ : 0 |x – x ₀ | , значения функции принадлежат окрестности бесконечно удаленной точки:
|f ( x ) | > M .
Бесконечный предел обозначают так:
.
Или при .

С помощью логических символов существования и всеобщности определение бесконечного предела функции можно записать так:
.

Также можно ввести определения бесконечных пределов определенных знаков, равных и :
.
.

Аналогичным образом вводятся определения односторонних пределов.
Левые пределы.
.
.
.
Правые пределы.
.
.
.

Определение предела функции по Гейне

Число a (конечное или бесконечно удаленное) называется пределом функции f ( x ) в точке x ₀ :
,
если
1) существует такая проколотая окрестность точки x ₀ , на которой функция определена;
2) для любой последовательности < x_n > , сходящейся к x ₀ : ,
элементы которой принадлежат окрестности , последовательность < f ( x_n )> сходится к a :
.

Если в качестве окрестности взять левостороннюю окрестность точки x ₀ , то получим определение левого предела. Если правостороннюю – то получим определение правого предела.

Определения предела по Гейне и Коши эквивалентны.

Примеры

Все примеры Далее мы приводим подробные решения задач, в которых нужно показать существование пределов, используя определение предела по Коши.
⇓, ⇓, ⇓.

Пример 1

Все примеры ⇑ Используя эпсилон и дельта — рассуждения показать, что
.

Введем обозначения:
.
Выпишем определение конечного предела функции в точке по Коши:
.
Преобразуем разность:

.

Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .

Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .

Пример 2

Все примеры ⇑ Используя определение предела по Коши показать, что
.

Введем обозначение:
.
Выпишем определение предела функции в точке , равного бесконечности, по Коши:
.
Выразим многочлены в числителе и знаменатели через многочлены от .
;
.

Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .

Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .

Пример 3

Все примеры ⇑ Используя определение предела по Коши показать, что
.

Введем обозначение:
.
Выпишем определение левого предела в точке , равного , по Коши:
.
В нашем случае .
Выразим многочлены в числителе и знаменатели через многочлены от .
;

.

Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .

Поскольку всегда можно уменьшить, то возьмем . Тогда для любого ,
при .
Это означает, что .

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов . Опубликовано: 12-05-2018

2. Предел функции в точке

Теория:

Рассмотрим функцию, график которой изображён на рисунке:

Для заданного случая предел функции y = f ( x ) при стремлении \(x\) к \(a\) равен \(b\). Записывают: lim x → a f ( x ) = b .

Эта запись отражает следующее: при выборе значений аргумента наиболее близко к значению \(x=a\), соответствующие значения функции приближаются всё ближе к предельному значению \(b\).

То есть f ( x ) ≈ b при \(x\), попадающем в достаточно малую окрестность точки \(a\). Причём, чем меньшая окрестность выбирается, тем точнее приближённое равенство.

Обратим внимание, что сама точка \(x=a\) при этом не рассматривается.

Функцию y = f ( x ) называют непрерывной в точке \(x=a\) , если выполняется соотношение:

lim x → a f ( x ) = f ( a ) .

То есть функция y = f ( x ) является непрерывной в точке \(x=a\), если предел функции y = f ( x ) при \(x\), стремящемся к \(a\), равен значению функции в точке \(x=a\).

Функцию y = f ( x ) называют непрерывной на промежутке \(X\), если она непрерывна в каждой точке промежутка.

Функция y = f ( x ) , составленная из рациональных, иррациональных, тригонометрических и обратных тригонометрических выражений , является непрерывной в любой точке области определения.

Что такое предел функции

В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.

Определение предела функции

Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.

Запись предела:

• предел обозначается значком lim;
• под ним добавляется, к какому значению стремится аргумент (переменная) функции. Обычно, это x , но не обязательно, например: “ x →1″;

Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):

Читается как “предел функции при икс, стремящемся к единице”.

x →1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).

Решение пределов

С заданным числом

Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x →1):

Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).

С бесконечностью

В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:

Если x →∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:

• 3 – 1 = 2
• 3 – 10 = -7
• 3 – 100 = -97
• 3 – 1000 – 997 и т.д.

Другой более сложный пример

Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.

Таким образом при “икс”, стремящемся к бесконечности, функция неограниченно растет.

С неопределенностью (икс стремится к бесконечности)

В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.

Пример: давайте вычислим предел ниже.

Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:

Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:

1. Находим x в старшей степени для числителя (в нашем случае – это два).

2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).

3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.

4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.

С неопределенностью (икс стремится к конкретному числу)

И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.

В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.

Пример: Найдем предел функции ниже.

1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.

2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.

В нашем случаем корнями выражения в числителе () являются числа 1 и 1,5. Следовательно его можно представить в виде: .

Знаменатель () изначально является простым.

3. Получаем вот такой видоизмененный предел:

4. Дробь можно сократить на ():

5. Остается только подставить число 1 в выражение, получившееся под пределом: