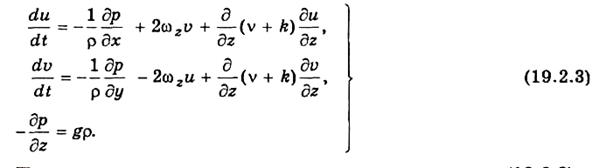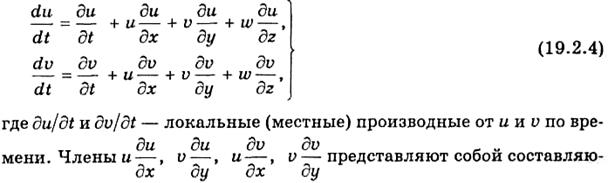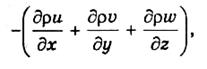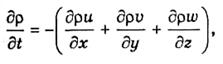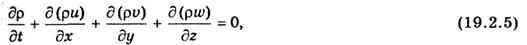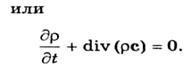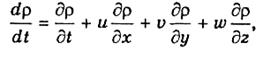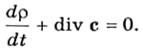Уравнение притока тепла в турбулентной атмосфере

Первое начало термодинамики для атмосферы

ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ В АТМОСФЕРЕ

Первое начало термодинамики для атмосферы

Атмосфера представляет собой воздушную среду, в которой постоянно осуществляется переход энергии из одного вида в другие. Раздел метеорологии, рассматривающий общие закономерности преобразования энергии и изменения состояния атмосферы под влиянием притока тепла называется термодинамикой атмосферы.

В этом разделе широко используются выводы, вытекающие из первого начала термодинамики или закона сохранения энергии:

ü Невозможно возникновение или уничтожение энергии, возможен лишь переход одних видов энергии в другие.

Количественно это положение выражается в виде

уравнения первого начала термодинамики или

уравнения притока тепла.

Для вывода этого уравнения выделим в атмосфере частицу сухого воздуха единичной массы. К характеристикам, определяющим состояния этой частицы относятся р_i, ρ_i,T_i, а к характеристикам, определяющим состояние окружающего эту частицу воздуха р_е, ρ_е, Т_е.

В силу малой скорости движения частицы (по сравнению со скоростью звука), можно ввести допущение, что между характеристиками окружающего воздуха и выделенной частицы выполняются квазистатические условия, т. е.: р_i = p_e= p.

Рассмотрим изменение характеристик выделенной частицы при получении этой частицей количества тепла, равного dg. Это количество тепла будет израсходовано на увеличение внутренней энергии и

совершение работы на увеличение объема, занимаемого данной частицей.

В этом случае ее внутренняя энергия увеличится на du и совершится работа dw против внешних сил давления на увеличение объема:

Для идеального газа, к которому можно отнести и сухой и влажный ненасыщенный воздух, изменение внутренней энергии частицы справедливо выражение:

где c_v — удельная теплоемкость сухого воздуха при постоянном объеме (v = const). Работа по расширению объема частицы определяется из выражения:

где dv_i– приращение объема частицы.

С учетом полученных выражений (3.2) и (3.3) уравнение первого начала термодинамики для выделенного объема воздуха примет вид:

После преобразования выражения (3.4) получим:

Для изобарического процесса (dр = 0) выражение (3.7) примет вид:

Для данного вида процесса справедливо выражение:

где с_р — удельная теплоемкость воздуха при постоянном давлении.

Соотношение (3.11) носит название уравнения Майера.

Для сухого воздуха: c_v = 718 Дж/кг К, а с_p = 1006 Дж/кг К,

. (3.13)

Подставим (3.10) в (3.7), тогда с учетом (3.5) получим

уравнение первого начала термодинамики:

. (3.14)

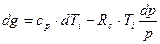
3.2. Адиабатический процесс

Термодинамический процесс называется адиабатическим, если он протекает без теплообмена частицы с окружающей средой.

При адиабатическом процессе dg = 0. Для такого процесса уравнения

(3.4) и (3.14) принимают вид:

. (3.16)

Уравнение (3.15) показывает, что при адиабатическом процессе работа против внешних сил давления совершается только за счет внутренней энергии.

При этом, если работа положительная, т.е. направленная на расширение объема (dv_i > 0), то внутренняя энергия частицы уменьшается (dТ_i 0), ее внутренняя энергия растет (dТ_i > 0).

При подъеме частицы объем ее увеличивается (dv_i > 0), а давление падает (dр

Подставим (3.19) в (3.17) и после сокращения запишем:

(3.20)

Разделим выражение (3.20) на выражение (c_p · dz):

(3.21)

Полученное выражение (3.21) определяет изменение температуры воздушной частицы, отнесенное к единице высоты при адиабатическом процессе.

ü Данное выражение показывает, что при адиабатическом подъеме воздушной частицы температура ее всегда падает

Это связано с тем, что при подъеме воздушной частицы происходит расход внутренней энергии на работу расширения.

Сухоадиабатическимградиентом называется падение температуры при адиабатическом подъеме сухой воздушной частицы, отнесенное к единице высоты:

. (3.22)

Подставим (3.22) в (3.21) и получим:

(3.23)

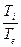
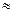
Для реальной атмосферы 1. Следовательно, сухоадиабатический

градиент для реальной атмосферы – величина постоянная (const).

(3.24)

Приближенно можно считать, что температура адиабатически подни­мающейся воздушной частицы падает примерно на один градус при подъеме на каждые 100 м высоты.

Изменение с высотой температуры адиабатически поднимающейся воздушной частицы графически изображается в осях координат – температура – высота, в виде прямой линии. Она называется сухоадиабатой или кривой состояния сухой воздушной частицы.

3.4. Потенциальная температура

Потенциальной температурой ( ) называется температура, которую примет воздушная частица, если ее переместить сухоадиабатически с исходного уровня до уровня с давлением 1000 гПа.

Приближенное выражение для расчета потенциальной температуры имеет вид:

(3.25)

где р₀ – давление воздуха на поверхности Земли;

Т_i – температура воздуха на исходной поверхности;

z – расстояние перемещения частицы по вертикали.

В выражении (3.25) последнее слагаемое правой части представляет собой изменение температуры частицы при перемещении ее от поверхности Земли до уровня 1000 гПа.

Если давление воздуха у поверхности Земли менее 1000 гПа, то уровень 1000 гПа лежит ниже поверхности Земли. Поэтому при дополнительном перемещении частицы от поверхности земли до уровня 1000 гПа частица нагревается.

Потенциальная температура обладает важными свойствами.

§ При сухоадиабатическом перемещении частицы ее потенциальная температура сохраняет постоянное значение, хотя ее температура (как степень нагретости) изменяется.

Это свойство сохранения (консервативности) потенциальной темпера­туры используется в качестве характеристики воздушных масс и оценки их вертикальных перемещений.

§ Если при перемещении частицы ее потенциальная температура изменилась, то это свидетельствует о притоке, либо оттоке тепла.

Другим свойством потенциальной температуры является ее связь с пол­ной энергией воздушной частицы.

§ При адиабатическом перемещении частицы ее полная энергия не изменяется.

3.5. Критерии устойчивости атмосферы на основе метода частицы

Распределение температуры окружающего частицу воздуха в различных слоях атмосферы характеризуется вертикальным градиентом температуры

(3.26)

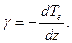
Распределение температуры и других метеорологических величин по высоте называется стратификацией атмосферы.

Для определения устойчивости к движению воздуха выделим в атмо­сфере воздушную частицу единичного объема. Характеристикой изменения температуры частицы является сухоадиабатический градиент при ее адиабатическом перемещении.

При вертикальном движении частицы возможны три случая с разными соотношениями между вертикальным и сухоадиабатическим градиентами.

Первый случай: > _а. Данное соотношение свидетельствует о том, что температура воздуха в атмосфере падает с высотой быстрее, чем на 1°С/100м. На воздушную частицу действуют две силы: сила тяжести и сила Архимеда. Результирующая величина этих сил называется силой плавучести.

При _е > _i, эта сила направлена вверх, а при _{е а} называется сухонеустойчивой.

Второй случай: = _а. В этом случае при перемещении частицы с исходного уровня, на котором Т_i = Т_е, а ,на любой другой уровень, температура и плотность частицы будут равны температуре и плотности окру­жающего ее воздуха. В соответствии с выражением (3.27) ускорение ее дви­жения будет равно нулю.

Термическое состояние атмосферы в этом случае при называется сухобезразличной (равновесной) стратификацией

Третий случай: 0;

Уравнения движения турбулентной атмосферы

Рассмотрим единичный объем воздуха, имеющий массу ρ. В об­щем случае на него действуют силы:

а) результирующая всех сил давления — градиент давления G; б) отклоняющая сила вращения Земли К; в) результирующая всех напряжений трения (молекуляр­ного и турбулентного) R; г) сила тяжести Р = pg. Если эти силы не уравновешиваются, то выделенный объем воздуха придет в движе­ние. По второму закону Ньютона произведение массы тела р на ускорение движения dc/dt равно сумме всех действующих на тело сил:

Это уравнение носит название уравнения движения атмосферы в векторной форме.

В метеорологии уравнения движения записывают обычно в ска­лярной форме. Прямоугольная (правая) система координат выби­рается так (см. рис. 19.1), чтобы плоскость хоу совпадала с горизон­тальной плоскостью, а ось оz — с вертикалью (положительное на­правление — вверх). Начало координат обычно помещается на уров­не моря.

Проектируя правую и левую части уравнения (19.2.1) последова­тельно на оси х, у, z, получаем с учетом результатов п. 19.1 систему уравнений движения атмосферы в координатной форме:

Систему уравнений (19.2.2) чаще всего записывают так, чтобы в левых частях стояли проекции ускорения. Для этого необходимо правую и левую части каждого уравнения последней системы разде­лить на плотность ρ. Третье уравнение движения, как показывает количественная оценка порядка величины различных членов, в бо­льшинстве случаев (но не во всех) сводится к основному уравнению статики.

В первых двух уравнениях системы (19.2.2) члены, содержащие вертикальную проекцию скорости, малы по сравнению с другими членами. Кроме того, часто пренебрегают изменением плотности с высотой. С учетом отмеченного запишем систему уравнений движе­ния атмосферы окончательно в следующем виде:

Подчеркнем, что производные в левых частях систем (19.2.2) и (19.2.3) представляют собой проекции ускорения движущегося объ­ема воздуха, т. е. являются индивидуальными производными от проекций скорости ветра по времени. Индивидуальные производ­ные записываются в виде

щиеинерционной силы (в частном случае — центробежной силы). Подчеркнем, что и, v, w в (19.2.2), (19.2.3) и (19.2.4) представляют собой проекции средней скорости движения атмосферы (средней скорости ветра).

При изучении большинства явлений и процессов в метеорологии воздух рассматривается как идеальный газ, удовлетворяющий усло­вию сплошности среды. Это означает, что всякий малый объем (эле­мент) воздуха считается все же настолько большим, что содержит очень много молекул. Именно в таком смысле следует понимать вы­ражения „частица воздуха», „бесконечно малая частица», „элемен­тарный объем» и др. Для таких сплошных сред справедливо уравне­ние неразрывности, именуемое также уравнением сплошности сре­ды. Физически оно выражает факт неуничтожаемости массы жид­кости или газа (в нашем случае — воздуха).

Через единичную площадку (1 м 2 ), перпендикулярную оси х, за единицу времени проходит масса воздуха, заключенная в объеме и · 1 м 2 , т. е. равная ри. Поскольку, согласно определению, масса воз­духа, которая проходит через единичную площадку за 1с, представ­ляет собой поток массы, то приходим к заключению, что проекции этого потока на оси х, у, z равны

Дивергенция потока массы (взятая с обратным знаком):

согласно теореме, доказанной в п. 9.4, равна притоку массы к еди­ничному объему за 1с. Приток же, в свою очередь, вызовет измене­ние массы единичного объема (которая равна р) во времени. За еди­ницу времени (1с) изменение массы равно dp/dt. Приравнивая изме­нение массы (dp/dt) к ее притоку

приходим к уравнению неразрывности, или сплошности среды:

Выполнив дифференцирование произведений ри, ри, pw и вос­пользовавшись выражением для полной производной от р по t

приходим ко второму виду уравнения неразрывности

Полученные в этой главе уравнения движения атмосферы (19.2.3), уравнение неразрывности (19.2.5) вместе с выведенными в других главах уравнениями переноса тепла и влаги и уравнением состояния воздуха составляют систему основных уравнений метео­рологии, или (по предложению И. А. Кибеля) систему уравнений погоды. Дополнительными уравнениями метеорологии служат урав­нения переноса лучистой энергии, уравнение Клаузиуса—Клапей­рона и некоторые другие уравнения, которые привлекаются при ре­шении частных задач.

В общем случае система уравнений метеорологии исключитель­но сложна не только с точки зрения ее решения (эти трудности с по­мощью численных методов и вычислительной техники в настоящее время постепенно преодолеваются), но и с точки зрения физическо­го содержания (вида) отдельных членов этой системы.

При изучении конкретных атмосферных явлений и процессов система уравнений погоды всегда упрощается, в одних случаях до­статочно обоснованно, путем строгих оценок порядка величины от­дельных членов уравнений, в других — менее обоснованно, на осно­ве различных предположений.

Поскольку уравнения метеорологии являются дифференциаль­ными уравнениями в частных производных, для построения конк­ретного их решения необходимо задать начальное и граничные условия. Вид последних зависит от физического содержания изуча­емого явления или процесса.

Уравнение притока тепла в турбулентной атмосфере

Основу прогностических моделей атмосферы составляют уравнения движения, притока тепла, неразрывности, переноса влаги и атмосферных примесей, являющиеся математическим выражением законов физики (это законы сохранения импульса, энергии и массы), а также уравнения состояния.

Для идеальной атмосферы (без учета турбулентной вязкости) в локальной декартовой системе координат (ось х направлена на восток, ось у – на север, ось z – по местной вертикали). уравнения гидротермодинамики представляют собой дифференциальные уравнения и содержат производные по времени (t) или по координатам и имеют следующий вид:

Уравнение притока тепла, влаги:

В (1)–(7) p, ρ и Т – давление, плотность и температура воздуха, и, v, w – проекции вектора скорости V на оси х, y, z соответственно; g – вектор силы тяжести, отнесенный к единице массы; ω – вектор угловой скорости вращения Земли, R – удельная газовая постоянная сухого воздуха; ε_л – скорость изменения количества тепла в единице объема за единицу времени за счет лучистого теплообмена, ε_п – скорость изменения количества водяного пара; c_p – удельная теплоемкость воздуха при постоянном давлении, γ_а – сухоадиабатический градиент температуры; l = 2ω sin φ – параметр Кориолиса, l₁ = 2ω cos φ, φ – широта места.