Уравнение проективной прямой на проективной плоскости

Введение (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5

Пусть М – произвольная точка плоскости и пусть эта точка имеет проективные координаты (х1, х2, х3). Проектируем точку Е на прямые А3Y¥, А3X¥ (рис.22).

На расширенной плоскости рассмотрим аффинный репер R = <А3, >.Обозначим аффинные координаты точки М(х, у). Таким образом, репер R¥ = <X¥, Y¥, А3 E> порождает на расширенной аффинной плоскости аффинный репер = <А3, >, где. причем проективные координаты (х1, х2, х3) называют однородными координатами точки М на расширенной плоскости, а (х, у), где , — неоднородными координатами точки М.

На расширенной плоскости задан проективный R = <X¥, Y¥, A3, E> построить точку M (4, -1, 2) по её координатам в репере R.

Две вершины координатного треугольника несобственные:

X¥ Î 2, Y¥ Î 3, È Y¥ = 3. È X¥ =

Строим проекции Е3 и Е2 точки E на прямые 2 и 3.

E3 = (EX¥) Ç 3, E2 = (EY) Ç 2.

Проективный репер R = <X¥, A3, E> порождает аффинный репер = <A3, >, где

Данная точка М будет относительно аффинного репера иметь координаты , .

Подставляя вместо х1, х2, х3 заданные координаты точки М, мы получим, что М имеет аффинные координаты (2, – ).

Построим точку М(2, –) в репере = <A3, > (рис.23). М – искомая точка.

Задачи для самостоятельного решения.

1. На расширенной прямой задан проективный репер R = <A1, A2, E>. Построить точку М(–2, 1) по её координатам в этом репере.

2. На расширенной прямой задан проективный репер R = <A1, M¥, E>. Построить точку М(2, 1) по её координатам в репере R.

3. На расширенной прямой задан проективный репер R = <A1, A2, E>, где Е – середина отрезка A1A2. Найти координаты несобственной точки M¥ прямой относительно репера R.

4. На расширенной прямой заданы точки A1,A2. Построить единичную точку Е проективного репера R = <A1, A2, E>, если известно, что несобственная точка M¥ прямой имеет координаты M¥(–1, 2) в репере R.

5. На расширенной плоскости задан проективный репер R = <A1, A2, A3, E>. Построить точку М(1, 2, 1) по её координатам в репере R.

6. Точка Е – центр тяжести D A1A2A3 на плоскости . Построить точку М(1, 1, –1) по её координатам в проективном репере R = <A1, A2, A3, E> на расширенной плоскости .

7. На расширенной плоскости задан проективный репер R = <A1, A2, M¥, E>. Построить точку М(1, 1, 2) по её координатам в репере R.

§4. Уравнение прямой

Пусть на проективной плоскости выбран проективный репер R = <A1, A2, A3, E>. Прямая d задана точками А(a1, a2, a3) и В(b1, b2, b3). Найдем уравнение прямой d.

Возьмем точку М принадлежащую прямой d. Пусть точка М имеет координаты (х1, х2, х3)относительно проективного репера R. Рассмотрим векторы , , , порождающие точки А, В и М соответственно. Так как точки А, В и М коллинеарны, то есть лежат на одной прямой, то векторы , , линейно зависимы, то есть один из них является линейной комбинацией других: = l + l, где (a1, a2, a3) и (b1, b2, b3). Последнее векторное равенство запишем в координатной форме:

,

, (1)

.

Уравнения (1) называют параметрическими уравнениями прямой d, l и m любые действительные числа, не равные нулю одновременно, называются параметрами.

Так как векторы , , линейно независимы, то

=0 (2)

(2) – уравнение прямой, проходящей через две точки.

Разложим определитель третьего порядка (левой части уравнения (2)) по элементам первой строки, получим:

u1 = , u2 = , u3 = .

Так как rg=2 то миноры второго порядка не равны нулю одновременно .

(u1, u2, u3) называют координатами прямой.

Координаты прямой определяются с точностью до постоянного множителя.

На проективной плоскости задан репер

R = <A1, A2, A3, E>. Еa – проекция точки Е из центра Аa на прямую (АbАg) (a, b, g = ). Найти уравнения координатных прямых (АaАb) и (АaЕa) относительно R.

Так как точки A1, A2 имеют кооординаты A1(1, 0, 0), A2(0, 1, 0), то уравнение прямой (A1A2) имеет вид:

или х3 = 0.

Аналогично получаем уравнения двух других координатных прямых:

Составим уравнение прямой (А1Е1):

Если точка А1 Î (А1Е1), то координаты этой точки удовлетворяют уравнению прямой:

Уравнение прямой примет вид:

Аналогично уравнения прямых:

Доказать, что точки А(а1, а2, а3), В(b1, b2, b3), С(с1, с2, с3) с координатами в проективном репере R = <A1, A2, A3, E> лежат на одной прямой тогда и только тогда, когда

Если точки А, В, С лежат на одной прямой, то векторы, их порождающие: , , линейно независимы, то есть

И обратно, пусть условие (1) выполнено, тогда векторы , , линейно зависимы. Значит, точки p() = А, p() = В, p() = С принадлежат одной прямой.

Найдите координаты точки пересечения прямых 2х1 + х2 + х3 = 0 и 3х1 + 3х2 + 2х3 = 0.

Точка пересечения заданных прямых удовлетворяет системе линейных уравнений:

Из курса алгебры известно, что общее решение этой системы находится по формулам:

x1 = l, x2 = l, x3 = l.

Поэтому для указанной системы x1 = –l, x2 = –l, x3 = 3l. Значит, точка пересечения имеет координаты
(–1, –1, 3).

Какова особенность расположения прямой (AB) относительно репера R = <A1, A2, A3, E> на проективной плоскости, если первые пары координат точек A(a1, a2, a3), B(b1, b2, b3) пропорциональны.

Запишем уравнение прямой (AB):

Разложив по элементам первой строки определитель, получим:

(AB): u1x1 + u2x2 = 0, где u1 = , u1 = .

Уравнению прямой (AB) удовлетворяют координаты A3 (0, 0, 1) вершины репера R. Следовательно, прямая AB проходит через координатную точку A3 проективного репера R.

Построить прямую x1 + 2x2 – 2x3 = 0 по её координатам относительно проективного репера R на расширенной плоскости.

Для построения прямой нужно знать две её точки. Найдём их, положим x1 = 0, x2 = 1. Тогда точка M имеет координаты (0, 1, 1). Аналогично, найдём вторую точку прямой N(2, 0, 1).

Построим точки М и N по их координатам относительно репера R на расширенной плоскости. Видим, что М = Е1 – проекция точки Е из А1. Точка N лежит на прямой А1А3, то есть N = N2. Строим проекцию N2 точки N из центра А2. Точка N2 имеет координаты (2, 1) относительно R2 = <A1, A3, E2>. Искомая прямая проходит через точки Е1 и N2.

Пусть на проективной плоскости заданы две различные прямые а: аaхa = 0 и b: baхa = 0 (a = ) своими уравнениями относительно репера R. Доказать, что уравнение:
(*) lаaхa + mbaхa = 0, где l и m принимают вещественные значения, не равные нулю одновременно, определяет пучок прямых на проективной плоскости.

1. Покажем, что любая прямая пучка, заданного парой пересекающихся прямых а и в, имеет уравнение (*).

2. Уравнение (*) есть уравнение прямой, принадлежащей пучку.

Возьмём любую прямую l пучка на проективной плоскости, заданную уравнением : u1x1 + u2x2 + u3x3 = 0. Так как прямые проходят через одну точку, то:

= 0, то есть

Уравнение прямой l запишется в виде:

Имеем уравнение (*). Покажем, что это уравнение определяет прямую, принадлежащую пучку, определяемому прямыми а и b.

Допустим противное, то есть

А это означает, что координаты прямых а и b пропорциональны. Получили, что прямые а и b совпадают, что противоречит условию задачи.

Значит, уравнение (*) определяет на Р2 прямую l.

Покажем, что точка С =а Ç b принадлежит прямой l, определяемой уравнением (*):

Подставим координаты точки С в уравнение (*):

То есть, уравнение (*) есть уравнение прямой, проходящей через точку С = а Ç b.

Задачи для самостоятельной работы.

1. Найти уравнение прямой на P2 относительно репера R = <A1, A2, A3, E> если она проходит через точки A(2, 3, 2), B(4, –1, 0).

2. Написать параметрические уравнения прямой, проходящей через точки A(1, 1, 2), B(2, 3, 1), имеющие координаты относительно репера R.

3. Найти точку пересечения прямых 2x1 – 3x2 + 5x3 = 0 и x1 + x2 + 3x3 = 0, имеющие данные уравнения относительно репера R.

4. Доказать, что на P2 прямая a(a1, a2, a3) с координатами относительно репера R = <A1, A2, A3, E> проходит через вершину Aa тогда и только тогда, когда aa = 0.

5. Какова особенность расположения точки M пересечения прямых a(a1, a2, a3), b(b1, b2, b3) относительно репера R если первые пары координат этих прямых пропорциональны?

6. Какова особенность прямой l(1, 1, 1) относительно проективного репера R = <A1, A2, A3, E> на расширенной плоскости, если единичная точка репера является точкой пересечения медиан координатного треугольника.

7. Доказать, что прямые a(a1, a2, a3), b(b1, b2, b3), c(c1, c2, c3) с координатами относительно репера R имеют общую точку тогда и только тогда, когда:

= 0.

8. Единичная точка E репера R = <A1, A2, A3, E> на расширенной плоскости является точкой пересечения медиан DA1A2A3. Найти координаты несобственных точек сторон DA1A2A3 и координаты несобственных точек его медиан относительно репера R.

9. Построить прямую a(1, 2, –2) по её координатам относительно заданного на расширенной плоскости проективного репера R = <A1, A2, A3, E>.

10. В пучке прямых на P2, заданном парой прямых
2x1 – 3x2 + 5x3 = 0 и x1 + x2 + 3x3 = 0 относительно репера R = <A1, A2, A3, E>, найти прямую проходящую через точку A(1, 1, 3).

§5. Преобразование проективных координат на проективной прямой и на проективной плоскости

1. Пусть на проективной плоскости R2 задан проективный репер R = <A1, A2, A3, E>. Наряду с проективным репером R возьмем еще один проективный репер R¢ = <A1¢, A2¢, A3¢, E¢>. Причем известно положение нового репера относительно старого, то есть известны координаты новых координатных точек A1¢, A2¢, A3¢ и единичной точки E¢ относительно репера R:

A1¢ = (),

A2¢ = (),

A3¢ = (), (1)

E¢ = ().

Пусть точки A1, A2, A3, E порождаются векторами , , . Причем будем считать, что система векторов <, , , > согласована с репером R, то есть вектор порождает точку A1, вектор – точку А2, вектор – точку А3, а их сумма + + порождает точку Е. В обозначениях, ранее введенных, это выглядит так:p() = A1, p() = A2, p() = A3, p() = Е, = + + .

Обозначим ¢, ¢, ¢, ¢ векторы, порождающие соответственно точки A1¢, A2¢, A3¢, E¢. Их можно разложить по векторам , , следующим образом (см. §3):

,

, (2)

,

.

Пусть М – произвольная точка проективной плоскости и пусть она имеет координаты (х1, х2, х3) в репере R, а в репере R¢ – М(у1, у2, у3). Найдем связь между координатами точки М относительно реперов R, R¢, то есть получим формулы, выражающие старые координаты точки М через её новые координаты.

Возможны 2 случая:

1. Система векторов ¢, ¢, ¢, ¢ согласована относительно репера R¢, то есть вектор ¢, порождающий точку E¢ равен сумме векторов, порождающих точки A1¢, A2¢, A3¢:

¢ = ¢ + ¢ + ¢ (3)

Из (2) и (3) следует, что в этом случае выполняется совокупность равенств (4):

,

, (4)

.

Из того, что точка М имеет координаты (х1, х2, х3) в репере R, следует, что вектор , порождающий точку М (p() = М), имеет координаты <х1, х2, х3> относительно базиса <, , >. Из того, что М(у1, у2, у3)R¢ следует, что вектор , имеющий координаты <у1, у2, у3> относительно базиса <¢, ¢, ¢> также порождает точку М. Тогда по первой аксиоме проективного простраенства = l, l ¹ 0. В последнем равенстве разложим векторы и по векторам соответствующих базисов:

у1¢ + у2¢ + у3¢ = l(х1 + х2 + х3).

Вместо ¢, ¢, ¢ подставим их разложения из формул (2)

у1 + у2 +
+ у3 = l(х1 + х2 + х3). (5)

Так как векторы , , линейно независимы, то, приравнивая коэффициенты при соответствующих векторах в левой и правой частях формулы (5), получим искомые формулы преобразования координат:

lх1 = у1 + у2 + у3,

lх2 = у1 + у2 + у3, (6)

ГЛАВА 3. ЛИНИИ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ

§17. Понятие проективной линии второго порядка

Множество всех точек проективной плоскости, координаты которых в некотором репере удовлетворяют действительному однородному уравнению второй степени, т.е. уравнению вида

a₁₁(x 1 ) 2 + a₂₂(x 2 ) 2 + a₃₃(x 3 ) 2 + 2 a₁₂x 1 x 2 + 2 a₁₃x 1 x 3 + 2 a₂₃x 2 x 3 = 0 (1)

называется линией или кривой второго порядка.

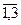
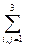
В однородном уравнении второй степени все действительные числа a_ij не обращаются одновременно в нуль. Положим для удобства a_ij = a_ji i,j = , тогда уравнение линии второго порядка можно записать в виде:

a_ij x i x j = 0

Если очевидны пределы суммирования, то, следуя правилу А.Эйнштейна, знак суммы можно опустить:

Понятие линии второго порядка является геометрическим и не зависит от выбора репера на проективной плоскости. Если фигура в репере Â = (A₁, A₂, A₃, E) имеет уравнение (2), а Â’ = (A’₁, A’₂, A’₃, E’) – другой проективный репер, формулы преобразования координат точек при переходе от репера Â к реперу Â’ представляются в следующем виде (см. §7,(3)):

λ x j = b j _i y i , j = 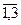, λ ≠ 0 (3)

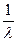
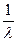
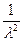
где (x 1 , x 2 , x 3 ) – координаты точки в репере Â, а (y 1 , y 2 , y 3 ) – координаты этой же точки в репере Â’. Подставляя выражения (3) в уравнение (2), имеем 0 = a_ij x i x j = a_ij ( b i _k y k ) ( b j _m y m ) = ( a_ij b i _k b j _m) y k y m .

Полагая a’_ij = a_rs b r _i b s _j, получаем уравнение линии второго порядка в репере Â’:

Замечание. Индексы, по которым идет суммирование, называются «слепыми», их можно переобозначать, например: b j _k y k = b j _p y p .

Заметим, что det(b j _k) 3 _i,k=1 ≠ 0. В курсе линейной алгебры доказывается, что при умножении матрицы A на невыраженную матрицу B ранг матрицы A не меняется.

Значит, rg(a_ij) 3 _i,j=1 = rg(a’_ij) 3 _i,j=1. Таким образом, в уравнении (4) не все коэффициенты при неизвестных равны нулю. Тем самым доказано, что, во-первых, понятие линии второго порядка не зависит от выбора репера, и, во-вторых, ранг матрицы, составленной из коэффициентов уравнения линии второго порядка, также не зависит от выбора репера. Таким образом, можно определить понятие ранга линии второго порядка, как ранг матрицы коэффициентов ее уравнения в некотором, а значит и в любом репере.

Линия второго порядка называется невырожденной, если ее ранг максимален, т.е. равен 3 (в этом случае det(a_ij) 3 _i,j=1 ≠ 0). И вырожденной, если rg(a_ij ) 3 _i,j=1 i x j = 0 (1)

В трехмерном векторном пространстве V 3 рассмотрим квадратичную форму q, т.е. для x(x 1 x 2 x 3 ) 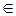V 3

q( ) = a_ij x i x j (2)

Из курса линейной алгебры известно, что в трехмерном векторном пространстве V 3 найдется базис, в котором квадратичная форма q имеет нормальный вид. Поскольку, согласно определению Г. Вейля, V 3 порождает проективную плоскость P 2 , то в P 2 найдется репер, в котором уравнение линии второго порядка имеет вид

где коэффициенты ε₁, ε₂, ε₃ равны -1, 1 или 0, но одновременно все три коэффициента не обращаются в нуль.

Таким образом, мы приходим к каноническому уравнению линии второго порядка.

Перебирая все возможные варианты для коэффициентов ε₁, ε₂, ε₃, убеждаемся, что на проективной плоскости существует пять типов линий второго порядка. Все они представлены в следующей таблице.

Указанные типы линий проективно различны, то есть не существует проективного преобразования, которое линию одного типа переводит в линию другого типа.

Однако, любые две линии одного и того же типа проективно эквивалентны.

Основное внимание в дальнейшем изложении мы будем уделять овальной линии.

Задача 43. Определить тип линии второго порядка

(x 1 ) 2 + 2x 1 x 2 + 2(x 2 ) 2 — (x 3 ) 2 = 0.

§19. Пересечение проективной линии второго порядка с прямой. Касательная к линии второго порядка.

Допустим, что задана невыраженная (т.е. максимального ранга) линия второго порядка, имеющая в некотором репере уравнение

Кроме того, прямая d, проходящая через точки P (p 1 , p 2 , p 3 ) и Q (q 1 , q 2 , q 3 ), имеет в этом же репере параметрические уравнения

x 1 = λ p 1 + μ q 1 ; x 2 = λ p 2 + μ q 2 ; x 3 = λ p 3 + μ q 3 (2)

Поставим задачу нахождения точек пересечения линии второго порядка с прямой d. Для решения этой задачи подставим x 1 , x 2 и x 3 из параметрических уравнений прямой d в общее уравнение линии второго порядка. Ясно, что мы получим однородное уравнение второй степени относительно λ и μ:

Можно посчитать коэффициенты A₁₁ A₁₂ A₂₂, из которых хотя бы один отличен от нуля:

Каждой ненулевой паре (λ, μ) действительных решений этого уравнения соответствует общая точка прямой и линии второго порядка. Однородное уравнение всегда имеет тривиальное решение, однако оно нам не подходит, так как, если λ = μ = 0, то x 1 = x 2 = x 3 = 0, но на проективной плоскости нет точки, все координаты которой равны нулю. Допустим, что μ ≠ 0, тогда легко получить квадратное уравнение:

A₁₁ 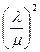+ 2A₁₂ + A₂₂ = 0 (5)

Исследуем дискриминант этого уравнения

= (A₁₂) 2 – A₁₁ A₂₂ (6)

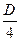
Если D > 0, то уравнение (5) и, соответственно, (3) имеет (с точностью до числового множителя) два непропорциональных вещественных решения относительно λ и μ. В этом случае прямая d пересекается с линией второго порядка в двух точках.

В каждой точке невыраженной линии второго порядка существует единственная касательная.

Если точка P (p 1 , p 2 , p 3 ) принадлежит линии второго порядка, то A₁₁ = a_ij p i p j = 0, и условие касания (7) принимает простой вид:

Расписывая соотношение (8), заменяя точку Q на текущую точку X(x 1 ,x 2 ,x 3 ), приходим к уравнению касательной:

Напомним, что мы полагаем a_ij = a_ji для любых индексов i, j от 1 до 3.

Задача 44. Овальная линия в каноническом репере задана уравнением

(x 1 ) 2 + (x 2 ) 2 — (x 3 ) 2 = 0

Написать уравнение касательной прямой, проходящей через точку P(1,1, ).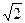

§20. Полюс, поляра, поляритет.

Пусть на проективной плоскости P 2 задана овальная линия γ, имеющая в некотором репере уравнение

Определение. Точки P (p 1 , p 2 , p 3 ) и Q (q 1 , q 2 , q 3 ) называются сопряженными относительно овальной линии, если выполняется условие

На первый взгляд может показаться, что сопряженность двух точек относительно овальной линии зависит от выбора репера, поскольку уравнение овальной линии рассматривается в определенном репере. Однако, как мы убедимся позже, сопряженность точек относительно овальной линии носит геометрический характер, то есть не зависит от выбора репера на проективной плоскости.

Если точка P лежит на овальной линии, то, вспоминая уравнение касательной прямой к линии второго порядка ((9) §19), убеждаемся, что точки P и Q сопряжены относительно γ тогда и только тогда, когда точка Q лежит на касательной к линии второго порядка в точке P.

Следующая теорема раскрывает геометрический смысл сопряженности двух точек, не лежащих на данной овальной линии.

Теорема. Пусть на проективной плоскости заданы овальная линия γ, и две точки P и Q, не лежащие на γ, причем прямая (PQ) пересекает γ в двух различных точках M и N. Для того, чтобы P и Q были сопряжены относительно γ, необходимо и достаточно, чтобы пара точек P и Q гармонически разделяла пару точек M и N, (т.е. чтобы сложное отношение четырех точек P, Q, M и N было равно -1: (PQ, MN) = -1.

Рис. 17.

Доказательство. Выберем на проективной плоскости произвольный репер R = (A₁, A₂, A₃, E), пусть в этом репере овальная линия имеет уравнение (1) и точки P и Q приобретают проективные координаты P (p 1 , p 2 , p 3 ) , Q (q 1 , q 2 , q 3 ); прямая (PQ) задается параметрическими уравнениями

x 1 = λ p 1 + μ q 1 ; x 2 = λ p 2 + μ q 2 ; x 3 = λ p 3 + μ q 3 (3)

Пусть точки пересечения прямой (PQ) и овальной линии имеют следующие координаты:

(PQ, MN) = (P′Q′, M′N′) = =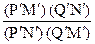
= =

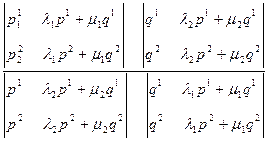
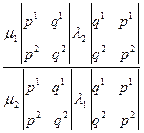
Заметим, что 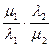= -1 тогда, и только тогда, когда = 0

Подставляя соотношение (3) в уравнение (1), получаем после деления на λ 2 :

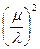
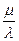
A₂₂ + 2A₁₂ + A₁₁ = 0 (4)

Поскольку точки P и Q не лежат на овальной линии, то A₂₂ = a_ijp i q j ≠ 0 A₁₁ = a_ij p i q j ≠ 0.

Так как точки M и N лежат на овальной линии, то = — .

Точки P и Q сопряжены относительно γ тогда и только тогда, когда a_ijp i q j = A₁₂= 0, т.е. P и Q сопряжены, если и только если = 0, что в свою очередь равносильно тому, что (PQ, MN) = -1.

Определение. Пусть на проективной плоскости задана овальная линия γ и точка P. Полярой называется множество точек d, сопряженных с точкой P относительно γ, а сама точка P называется полюсом поляры d.

Если овальная линия задается в некотором репере уравнением (1), точка P имеет координаты (p 1 , p 2 , p 3 ), то из условия сопряженности (2) получаем уравнение поляры d:

(a_i1p i ) x 1 + (a_i2p i ) x 2 + (a_i3p i ) x 3 = 0 (5)

Поскольку овальная линия невырождена, то не все коэффициенты при x 1 , x 2 , x 3 равны нулю, поэтому d – прямая. Для каждой точки P (p 1 , p 2 , p 3 ), проективной плоскости существует поляра (5) относительно овальной линии (1), и обратно для каждой прямой u₁ x 1 + u₂x 2 + u₃x 3 = 0 существует единственный полюс P, координаты которого определяются системой уравнений

Овальная линия не вырождена, определитель системы не равен нулю, поэтому точка P определяется однозначно (координаты точки P находятся с точностью до ненулевого множителя).

Таким образом, любая овальная линия определяет биекцию P 2 → (P 2 )′ проективной плоскости P 2 на множество (P 2 )′ ее прямых.

Теорема о взаимности поляритета. Пусть на проективной плоскости задана овальная линия. Если точка Q лежит на поляре точки P, то точка P лежит на поляре точки Q.

Задача 45. С помощью одной линейки (без циркуля) построить касательную, проходящую через заданную точку, к заданной овальной линии на расширенной плоскости.

Задача 46.Пусть на расширенной плоскости задана овальная линия. По данному полюсу построить поляру; по данной поляре построить полюс.

§21. Теорема Штейнера.

Теорема Штейнера позволяет дать геометрическое определение овальной линии второго порядка при помощи отображения одного пучка прямых на другой.

Теорема Штейнера. На проективной плоскости множество точек пересечения соответствующих прямых двух проективных, но не перспективных пучков есть невырожденная кривая второго порядка. И обратно, два пучка с центрами на кривой второго порядка, у которых соответствующие прямые пересекаются на этой кривой – проективны.

Доказательство. Пусть даны два пучка с различными центрами O₁ и O₂ и установлено проективное, но не перспективное отображение f первого пучка на второй. Докажем, что множество γ точек пересечения соответственных прямых этих пучков есть овальная линия, проходящая через точки O₁ и O₂.

Обозначим через m прямую (O₁O₂) и рассмотрим прообраз n этой прямой m=f(n). Отображение f зададим с помощью трех попарно различных прямых n, m, l пучка O₁ и их образов m, m′, l′ в пучке O₂:

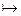
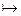
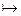
f: n m; m m′; l l′

Прямые n, m′, l′ попарно различны, так как f не является перспективным отображением, поэтому точки O₁=n∩m, O₂=m∩m′ и O₃=n∩m′ не лежат на одной прямой, точка E=l∩ l′ не принадлежит прямым m, m′, n, следовательно, мы получим репер Â = (O₁, O₂ , O₃ ,E,).

Пусть X (x 1 , x 2 , x 3 ) произвольная точка, не лежащая на сторонах трехвершинника O₁O₂O₃ . По определению сложного отношения прямых (mn, l(O₁ X)) = (O₂O₃,E₁,X₁), и (m′m, l′(O₂ X)) = (O₃O₁,E₂,X₂) (см. рисунок 18).

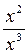
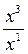
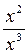
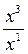
В репере R₂ = (O₂, O₃ ,E₁) на координатной прямой (O₁O₂) точка X₁ имеет координаты (x 2 , x 3 ), поэтому (O₂O₃,E₁,X₁) = . Аналогично, (O₃O₁,E₂,X₂) = . Таким образом, (mn, l(O₁X)) = ; (m′m, l′(O₂X)) = .

Если X 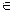γ, то в силу сохранения проективным отображением сложного отношения имеем (mn, l (O₁ X)) = (m′m, l′ (O₂X)).

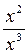
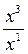
Поэтому = , и мы получаем уравнение линии второго порядка:

(x 1 x 2 ) — (x 3 ) 2 = 0 (1)

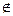
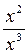
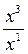
Если Х γ, то (mn, l (O₁X)) ≠ (m′m, l′ (O₂X)), и ≠ , т.е. координаты точки Х не удовлетворяют уравнению (1). Если точка X лежит на сторонах трехвершинника O₁O₂O₃, то ее координаты удовлетворяют уравнению (1), если, и только если Х совпадает с одной из точек O₁(1,0,0) и O₂(0,1,0), которые принадлежат множеству γ. Уравнение (1) есть уравнение второй степени, ранг максимален, следовательно, оно определяет невыраженную линию второго порядка, на которой есть действительные точки O₁ и O₂, т.е. овальную линию.

Обращая рассуждения, получаем вторую часть теоремы Штейнера.

Задача 47. Сформулировать предложение, двойственное теореме Штейнера.

§22. Теоремы Паскаля и Брианшона .

Если шестивершинник есть любая шестизвенная замкнутая ломанная, а под сторонами шестивершинника понимают прямые, содержащие звенья ломанной, то теорему Паскаля можно сформулировать следующим образом.

Теорема Паскаля. Противолежащие стороны шестивершинника, вписанного в овальную линию второго порядка, пересекаются в точках, лежащих на одной прямой.

Рисунок 19.

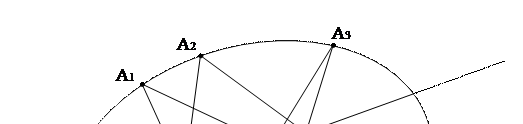Доказательство. Пусть вершины шестивершинника A₁ A₂ A₃ A₄ A₅ A₆ лежат на овальной линии γ. Докажем, что точки O = (A₁A₆) ∩ (A₃A₄), N = (A₂A₄) ∩ (A₁A₅) и N′ = (A₂A₆) ∩ (A₃A₅) лежат на одной прямой (см. рисунок 20).

Рисунок 20.

Пусть f – проективное отображение пучков с центрами A₁ и A₃, которое устанавливается овальной линией γ согласно теореме Штейнера. Отображение f порождает проективное отображение φ: (A₂, A₄)→(A₂, A₆), в которой каждой точке Х₁ на (A₂, A₄) соответствует точка Х₂ прямой (A₂,A₆), такая, что прямые (A₁, Х₁) и (A₃,Х₂) пересекаются в точке Х, принадлежащей линии γ. Поскольку φ(A₂)= A₂, то φ – перспективное отображение, центром его является точка O, причем N′ = φ(N), следовательно N, O, N′ принадлежат одной прямой.

Обратная теорема Паскаля. Если точки пересечения противоположных сторон шестивершинника лежат на одной прямой, то все его вершины лежат на овальной линии второго порядка.

Замечание. Если в теореме Паскаля овальную линию заменить на пару прямых, то мы приходим к теореме Папа.

Двойственной к теореме Паскаля является следующая

Теорема Брианшона. Шестивершинник описан около овальной линии второго порядка тогда и только тогда, когда его большие диагонали пересекаются в одной точке.

Задача 48. Даны пять точек общего положения и прямая, проходящая через одну из них и не проходящая через остальные точки. Построить вторую точку пересечения данной прямой с овальной линией, проходящей через данные пять точек.