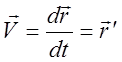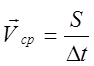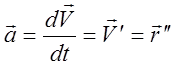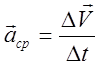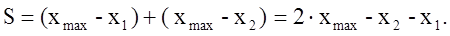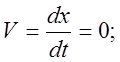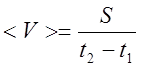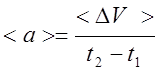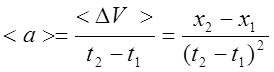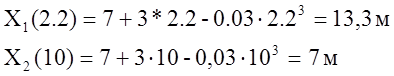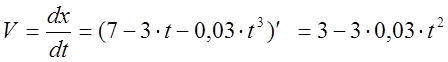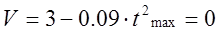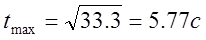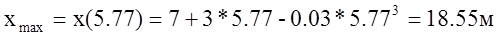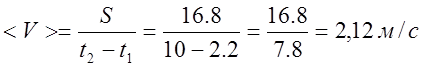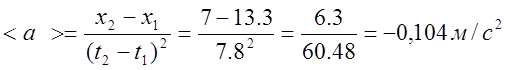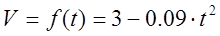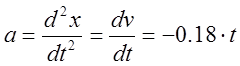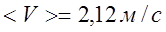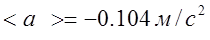Кинематика материальной точки. Кинематическое уравнение движения материальной точки по прямой
Страницы работы
Содержание работы
Министерство образования Российской Федерации
Санкт-Петербургский государственный горный институт им. Г.В. Плеханова
Кафедра общей и технической физики
Тема: «Кинематика материальной точки»
Выполнил: студент гр. БА-02 ________________ /Михалов А.И./
Проверил: доцент ________________ /Смирнова Н.Н./
(должность) (подпись) (Ф.И.О.)
1. Формулировка задания.
Кинематическое уравнение движения материальной точки по прямой (ось x) имеет вид,
1. Путь, пройденный материальной точкой за интервал времени от t1=2.2с до t2=10с.
2. Среднюю путевую скорость V за тот же интервал времени.
3. Среднее значение ускорения.
4. Координату материальной точки в момент времени t1 и t2
Построить графики зависимостей величин V(t), а(t) при изменении времени.
2 Краткое теоретическое содержание.
Основные определения
Исходное уравнение – х=f(t)=7+3t-0,02t 3 – уравнение зависимости координаты от времени. Данное уравнение является уравнением прямолинейного движения, т.к. изменяется только одна координата.
Материальная точка – тело, размерами которого можно пренебречь по сравнению с расстоянием до других тел.
Путь (S) – расстояние по траектории (от начала движения до данной точки). [S]=м
Скорость (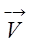
Среднепутевая скорость (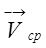
Ускорение (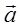
Среднее ускорение (аср) — физическая величина, которая равна отношению изменения скорости к интервалу времени.
Равнозамедленное прямолинейное движение – движение, при котором скорость материальной точки за равные промежутки времени изменяется на одну и тужу величину, причём направления вектора скорости и ускорения противоположны.)
Основные формулы, применяемые в работе.
1. Путь, пройденный материальной точкой за интервал времени от t1до t2:
Для определения пути разобьем его на два, т.к. при изменении знака проекции скорости, точка изменяет направление движения и начинает двигаться в обратном направлении:
где S1— путь, пройденный материальной точкой за время t max-t 1;
S2 — путь, пройденный материальной точкой за время t 2-t max;
t max– время в момент возврата материальной точки (когда точка начинает двигаться в обратном направлении: путь возрастает, а координата материальной точки убывает).
Чтобы найти формулы вычисления S1 и S2, схематично изобразим данное движение:
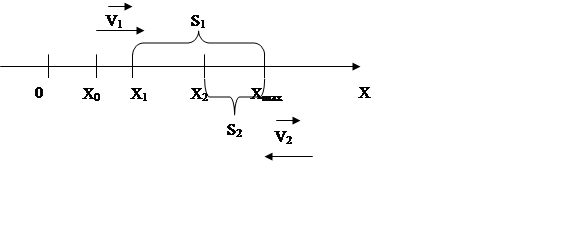 |
Из данного рисунка видно, что путь равен приращению координаты:
где x1,x2 – координаты точки в моменты времени t 1 и t 2 соответственно;
xmax – максимальная координата, которую материальная точка достигает в момент, когда начинает двигаться обратно (скорость меняет знак).
2. t max определяется приравниванием к нулю первой производной от координаты по времени, т.к. по свойству максимума в точке, в которой функция х=f(t) максимальное значение, первая производная этой функции равна нулю. Т.к. при данном движении все переменные изменяются только по координате Х, то приращение (дифиренцал) радиус-вектора равно приращению (дифиренцалу) координаты (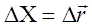
3. Средняя путевая скорость Vср за тот же интервал времени (в соответствии с определением):
4. Среднее значение ускорения (в соответствии с определением):
Т.к. скорость равна отношению приращения радиус вектора к интервалу времени, за которое это приращение произошло, то можно записать данную формулу следующим образом:
Данное кинематическое уравнение движения материальной точки 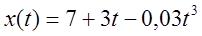
3.1. Координаты материальной точки в моменты времени t 1 и t 2 определяются подстановкой соответствующих значений моментов времени:
3.2. Для определения момента возврата найдём первую производную от координаты по времени.

3.3. Время в момент возврата материальной точки:
3.4. Максимальная координата
Подставив, значение момента возврата материальной точки в уравнение координаты определим:
3.5. Путь, пройденный материальной точкой за интервал времени от t1до t2:
3.6. Средняя путевая скорость Vср за тот же интервал:
3.7. Среднее значение ускорения:
Уравнение зависимости скорости от времени уже найден в пункте 3.2 (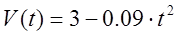
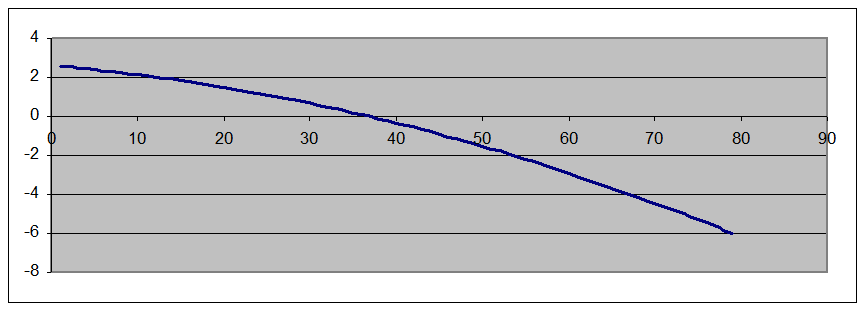
График зависимости скорости от времени.
Потому что точка меняет направление движения в момент времени t=5,77 с., график зависимости скорости от времени пересекает ось Х.
Найдём уравнение мгновенного ускорения в произвольный момент времени t. Для этого возьмём вторую производную от координаты x:
График зависимости а(t) представляет собой прямую. .
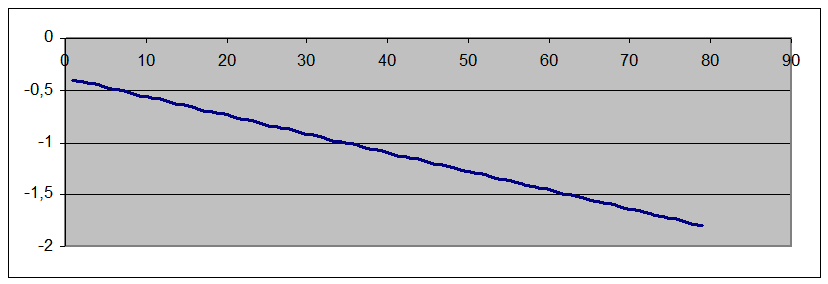 |
Вывод: В расчетно-графическом задании “Кинематика материальной точки” рассматривалось движения материальной точки по прямой. В результате решения я нашёл:
2.
3.
Построенные графики отображают зависимость а(t) и V(t).
Уравнение движения материальной точки
Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.
Имеет смысл говорить только о движении в некоторой системе отсчета.
Система отсчета. Системы координат
Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.
В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:
- сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
- цилиндрическая система с координатами p , z , α ;
- на полярной плоскости с параметрами r , φ .
В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.
Кинематическое уравнение движения материальной точки
Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.
При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.
Это возможно при использовании кинематического уравнения движения:
Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.
Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:
x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .
Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.
Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.
Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:
r = r ( t ) , φ = φ ( t ) ( 3 ) .
Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как
q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .
Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.
Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:
Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.
Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.
Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.
Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.
Дано: x = 0 , 4 t 2 , t = 4 c
Найти: υ x ( t ) , S — ?
Решение
При решении необходимо учитывать зависимость скорости от времени:
υ x = υ 0 x + a x t .
Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:
x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .
Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .
После подстановки данных в уравнение:
Определим точки, изобразим график:
υ x = 0 , t = 0 , υ x = 4 , t = 5
Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:
Формула пути
Определение и формула пути
Линия, которую описывает материальная точка при своем движении, называется траекторией.
Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени от t1 до t2.
В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:
В цилиндрических координатах длина пути может быть выражена как:
В сферических координатах формулу длины пути запишем:
Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением. Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t \rightarrow 0$ материальная точка проходит путь ds, который называют элементарным. При этом:
где $\bar
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути $\Delta s$ на отрезке времени от $t$ до $t + \Delta t$ находят как:
$$\Delta s=\langle v\rangle \Delta t(6)$$
где $\langle v\rangle$ – средняя путевая скорость. При равномерном движении $\langle v\rangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
Примеры решения задач
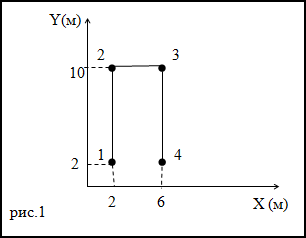
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой, чему равно перемещение, если точка двигалась 1-2-3-4.
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
Ответ. Путь равен 20 м, перемещение равно 4 м.
Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией: x=-0,2t 2 (м) . Какой путь пройдет материальная точка за 5 с?
Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения задачи примем формулу пути в виде:
Подставим в (2.1) функцию x=-0,2t 2 , учтем, что $0 c \leq t \leq 5 c$ имеем:
http://zaochnik.com/spravochnik/fizika/osnovy-dinamiki/uravnenie-dvizhenija-materialnoj-tochki/
http://www.webmath.ru/poleznoe/formules_21_27_put.php