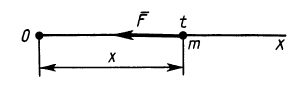
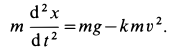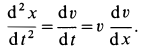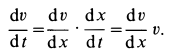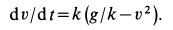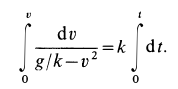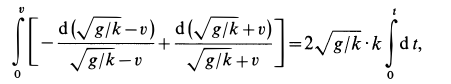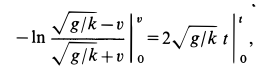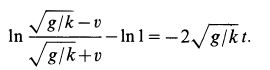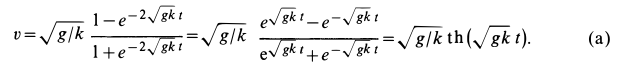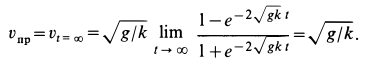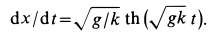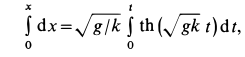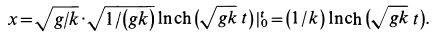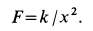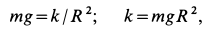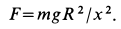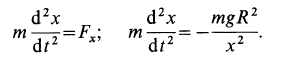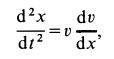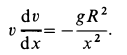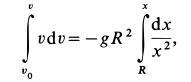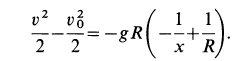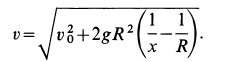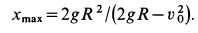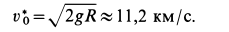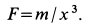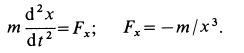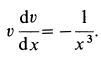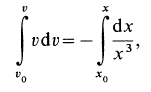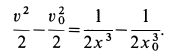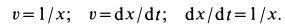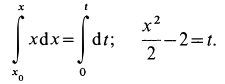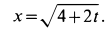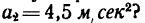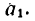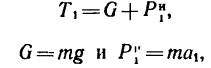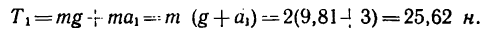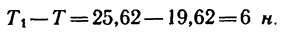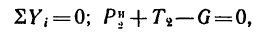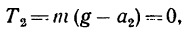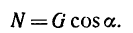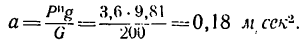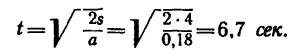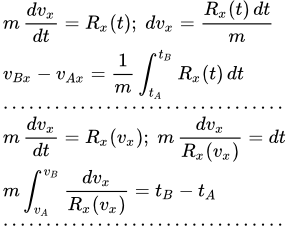Уравнение движения материальной точки
Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.
Имеет смысл говорить только о движении в некоторой системе отсчета.
Система отсчета. Системы координат
Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.
В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:
- сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
- цилиндрическая система с координатами p , z , α ;
- на полярной плоскости с параметрами r , φ .
В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.
Кинематическое уравнение движения материальной точки
Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.
При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.
Это возможно при использовании кинематического уравнения движения:
Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.
Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:
x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .
Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.
Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.
Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:
r = r ( t ) , φ = φ ( t ) ( 3 ) .
Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как
q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .
Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.
Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:
Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.
Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.
Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.
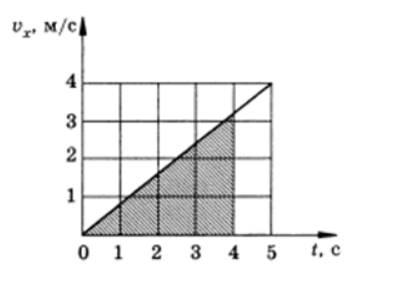
Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.
Дано: x = 0 , 4 t 2 , t = 4 c
Найти: υ x ( t ) , S — ?
Решение
При решении необходимо учитывать зависимость скорости от времени:
υ x = υ 0 x + a x t .
Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:
x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .
Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .
После подстановки данных в уравнение:
Определим точки, изобразим график:
υ x = 0 , t = 0 , υ x = 4 , t = 5
Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:
Прямолинейное движение точки в теоретической механике
Содержание:
Основные виды прямолинейного движения точки:
Дифференциальное уравнение прямолинейного движения точки вдоль оси
если рассматривается случай зависимости силы только от времени, координаты и скорости.
Начальные условия можно задать в форме 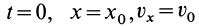
Наиболее важные случаи прямолинейного движения материальной точки получаются тогда, когда сила 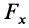
Силу, зависящую от координаты 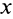
Отметим, что в перечисленных случаях интегрирование дифференциального уравнения (1Г) выполняется наиболее просто и его можно довести до конца в квадратурах. В более общем случае, если сила одновременно зависит от времени 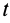
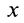
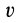
Рассмотрим примеры на составление и интегрирование дифференциального уравнения прямолинейного движения точки. Эти примеры позволяют выявить некоторые особенности решения таких задач. Ниже приведены примеры, когда сила зависит только от времени, или от скорости, или от координаты.
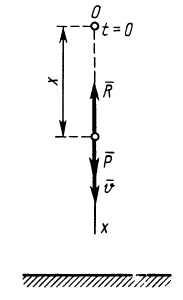
Пример 1. Точка массой 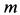
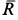
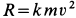
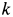
Найти уравнение движения точки.
Решение:
Направим ось 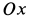
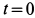
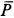
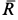
Скорость в этом случае можно определить в зависимости от времени или от координаты, используя подстановки
Последняя подстановка позволяет исключить из дифференциального уравнения время при определении скорости. Эта подстановка получается из первой умножением и одновременным делением на 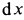
Используя первую подстановку, получаем дифференциальное уравнение движения точки в следующем виде:
Разделяя переменные и беря интегралы от обеих частей, имеем
Рис. 8
Для того чтобы не искать дополнительно произвольную постоянную интегрирования, интегралы возьмем определенные, сохраняя верхний предел переменным для последующего интегрирования, а для нижних пределов используем также условие: при 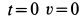
Потенцируя и решая относительно 
Переходя в (а) к пределу при 
Для достижения предельной скорости требуется бесконечно большое время. Более подробные расчеты показывают, что скорость, близкая к предельной, устанавливается довольно быстро.
Отметим, что для свободного падения в воздухе парашютиста вблизи Земли без раскрытия парашюта предельная скорость равна 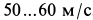
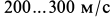
Для нахождения закона движения точки подставляем в (а) вместо скорости 
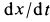
Интегрируя это уравнение после разделения переменных, имеем
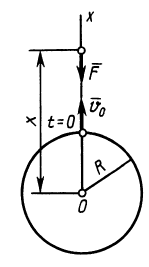
Пример 2. Материальная точка массой 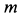
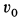
Определить зависимость скорости точки от ее расстояния до центра Земли, пренебрегая сопротивлением воздуха.
Решение:
Направив ось 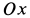
Постоянный коэффициент 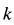
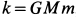
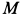
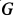
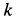
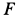
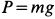
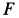
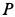
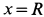
где 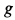
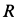
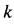
Составляем дифференциальное уравнение движения точки. Получаем
Рис. 9
Знак минус в правой части этого уравнения определяется знаком проекции силы 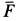
Исключая время из дифференциального уравнения подстановкой
Разделяя переменные и беря от обеих частей интегралы с учетом, что при 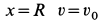
Для определения наибольшего расстояния 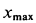
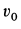
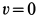
Видно, что 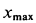
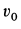
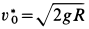
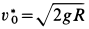
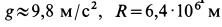
Скорость 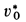
Наименьшую скорость космического корабля, при которой он становится спутником Земли, называют первой космической скоростью. Она приблизительно равна 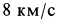
Пример 3. Материальная точка массой 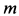
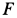
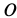
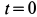
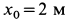
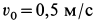
Рис. 10
Определить уравнение движения точки.
Решение:
Выбирая за начало координат точку 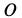
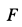
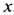
Учитывая направление силы 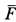
После преобразования левой части оно примет форму
Разделяя переменные и интегрируя это уравнение, имеем
После подстановки числовых значений для 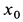
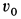
Интегрируя полученное уравнение, имеем
Закон движения точки можно выразить в форме
Прямолинейное движение точки
Обычно в задачах по динамике рассматривают так называемые несвободные материальные точки —материальные точки, движение которых ограничивается различными связями.
Приступая к решению задач, в которых рассматривается несвободная материальная точка, нужно прежде всего выявить действующие на точку активные силы (движущие силы и силы сопротивления), а также реакции связей (пассивные силы).
Выявив действующие силы, необходимо определить, находятся они в равновесии или нет? Этот вопрос в зависимости от заданных условий решается двояко.
Если, например, известно, что точка движется равномерно и прямолинейно, значит система сил уравновешена; если же известно, что точка двигается неравномерно или имеет криволинейную траекторию, то система сил неуравновешена.
Если система сил задана (все силы системы известны), то, определив проекции сил на оси координат, можно установить равновесие или неравновесие системы. В случае когда суммы проекций всех сил на каждую из осей равны нулю, заданная система сил уравновешена; когда же сумма проекций всех сил хотя бы на одну из осей не равна нулю, система сил неуравновешена; в первом случае точка движется равномерно и прямолинейно, во втором случае— имеет ускорение (вторая задача динамики).
При решении различных технических задач особенно важное значение приобретает случай, когда на материальную точку действует неуравновешенная система сил. В подобных случаях целесообразно решать задачи, применяя так называемый метод кинетостатики или принцип Даламбера, который формулируется так: активные силы, реакции связей и сила инерции образуют уравновешенную систему сил.
Применяя принцип Даламбера, необходимо очень хорошо понимать Сущность силы инерции. Нужно помнить, во-первых, что сила инерции, численно равная произведению массы точки на приобретенное ускорение, всегда направлена в сторону, противоположную вектору ускорения;
- во-вторых, что сила инерции в действительности не приложена к рассматриваемой в задаче материальной точке; она условно прикладывается к этой точке; фактически сила инерции приложена к двигающему телу или к связи;
- в-третьих, что равновесие сил, которое образуется после добавления силы инерции к силам, приложенным к точке, — равновесие фиктивное; но оно позволяет воспользоваться для решения задачи уравнениями равновесия из статики.
При решении задач с помощью метода кинетостатики рекомендуется придерживаться такой последовательности:
- выделить точку, движение которой рассматривается, и изобразить ее на рисунке;
- выявить все активные силы и изобразить их приложенными к точке на рисунке;
- освободить точку от связей, заменить связи их реакциями и также изобразить их на рисунке;
- добавить к полученной системе сил силу инерции;
- рассмотреть образовавшуюся уравновешенную систему сил и в зависимости от вида системы сил выбрать наиболее рациональный способ решения: графический, графо-аналитический или аналитический (методом проекций).
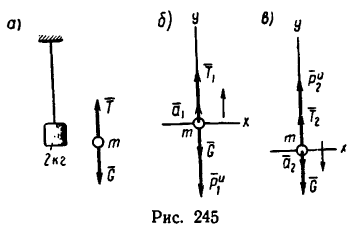
Задача №1
На шнуре подвешена двухкилограммовая гиря (рис. 245, а). Каково при этом натяжение шнура? Как изменится натяжение шнура, если при его помощи поднимать гирю вертикально вверх равномерно? Поднимать вертикально вверх с ускорением 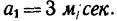
1. На гирю, которую принимаем за материальную точку массой m = 2кг, подвешенную на шнуре (см. рис. 245, а), действуют две силы: сила тяжести G и реакция нити Т, равная ее натяжению.
Других сил нет. Материальная точка (гиря) находится в покое, значит силы G и 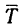
2. Если гиря, подвешенная на шнуре, поднимается вертикально вверх равномерно, то на нее действуют те же две силы и они также образуют уравновешенную систему. Происходит лишь замена статического равновесия (равновесия в состоянии покоя) динамическим равновесием (равновесием в состоянии движения — равномерного и прямолинейного).
Таким образом, и в этом случае (см. рис. 245, а) натяжение шнура T = G= 19,62 я.
3. Рассмотрим гирю в состоянии равноускоренного движения вертикально вверх с ускорением 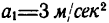
На гирю действуют также две силы: ее вес G и натяжение шнура 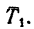
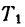
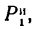
Система сил G, 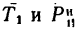
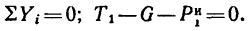
Из этого уравнения
поэтому
Как видно, при подъеме гири вверх с ускорением натяжение шнура увеличивается:
4- Рассмотрим гирю в состоянии равноускоренного движения вертикально вниз с ускорением 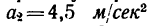
На гирю также действуют две силы: G и 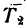
Добавим силу инерции 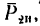
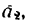
Уравнение равновесия примет вид
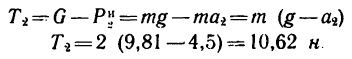
При ускоренном движении гири вниз натяжение шнура ослабевает. В данном случае по сравнению с состоянием равновесия натяжение шнура уменьшается на 9 н.
Примечание. Если решение задачи выполнить в технической системе единиц (МКГСС), то вес гири G= 2 кГ, а сила инерции получит такое выражение
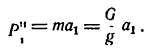
Тогда значение 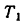
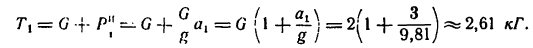
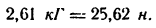
Отмстим, что выражение натяжения шнура при равноускоренном движении гири вниз
Если ускорение 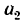
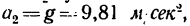
т. с. при свободном падении гири она не натягивает шнур. Образуется состояние «невесомости».
Задача №2
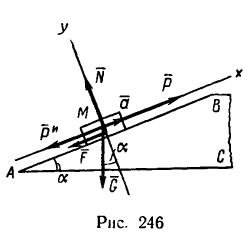
По наклонной плоскости АВ длиной 4 м и с углом подъема а=15 равноускоренно поднимают груз М весом G = 200 кГ, постоянной силой Р=65 кГ, направленной параллельно наклонной плоскости. Определить, сколько времени потребуется, чтобы переместить груз па расстояние AВ, сели коэффициент трения при движении груза по наклонной плоскости f= 0,05.
Решение — в единицах системы МКГСС.
1. Изобразим тело М на наклонной плоскости с приложенными к нему силами 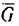
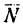
Находясь под действием этих сил, тело движется по наклонной плоскости с постоянным ускорением а.
2. Груз перемещается равноускоренно, без начальной скорости. Время его движения можно определить из уравнения движения
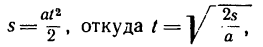
но предварительно необходимо определить ускорение а. Теперь система пяти сил 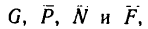
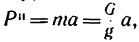
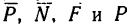
4. Выберем систему координат, как показано на рис. 238, и спроектируем все силы на оси х и у. Тогда получим два уравнения равновесия:
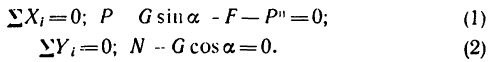
5. Из уравнения (1)
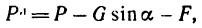
но сила трения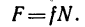
Нормальное давление найдем из уравнения (2):
поэтому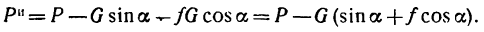
Подставим в это уравнение числовые значения 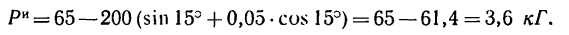
6. Из выражения 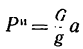
7. Подставив значение ускорения а в выражение 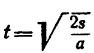
Рекомендуется повторить решение последней задачи в единицах СИ, а затем самостоятельно решить следующие задачи.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Относительное движение материальной точки
- Геометрия масс
- Кинематика сплошной среды
- Аксиомы классической механики
- Дифференциальные уравнения движения материальной точки
- Две основные задачи динамики точки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Интегрирование дифференциальных уравнений прямолинейного движения материальной точки
Краткое изложение результатов
Здесь мы кратко изложим основные результаты, полученные при интегрировании дифференциальных уравнений прямолинейного движения материальной точки. Далее следует их подробное изложение.
Сила, зависящая от времени
Если на материальную точку действует сила, зависящая от времени , то дифференциальное уравнение прямолинейного движения вдоль оси Ox имеет вид:
.
Вводим ускорение и интегрируем это уравнение.
.
Здесь и далее A и B – произвольные точки на оси Ox . Заменим . Получаем закон изменения скорости от времени:
.
Интегрируя уравнение , получаем закон движения точки :
;
.
Сила, зависящая от скорости
Пусть на точку действует сила, зависящая от скорости . Составляем дифференциальное уравнение движения и интегрируем его:
.
Последнее уравнение дает в неявном виде зависимость . Решаем его. После чего интегрируем уравнение , как описано выше.
Есть второй способ интегрирования уравнения движения в случае зависимости силы от скорости. Для этого переходим от переменных x и t к переменным и x . Считаем, что скорость является функцией от координаты x :
;
.
Последнее уравнение дает в неявном виде зависимость . Далее интегрируем уравнение :
.
Это уравнение дает в неявном виде закон движения точки .
Сила, зависящая от перемещения
Пусть на точку действует сила, зависящая от перемещения . Составляем уравнение движения, переходим от переменных x и t к переменным и x , и интегрируем полученное дифференциальное уравнение:
;
;
.
Это уравнение представляет собой закон сохранения механической энергии для прямолинейного движения. Из него находим зависимость скорости от перемещения . После чего интегрируем уравнение , как это описано выше.
Дифференциальное уравнение движения точки
Рассмотрим прямолинейное движение материальной точки, находящейся под действием постоянных и переменных сил. Направим ось Ox системы координат вдоль линии движения точки. Пусть на нее действуют n сил, проекции которых на ось Ox мы обозначим как . Положение точки, при прямолинейном движении, однозначно определяется ее координатой x . Нам нужно определить закон движения точки , то есть закон изменения ее координаты со временем.
Уравнение движения точки определяется вторым законом Ньютона, который в случае прямолинейного движения имеет вид:
(1) .
Вместо того, чтобы в каждом уравнении выписывать все n сил, введем их равнодействующую, проекция которой, на ось x равна сумме проекций всех сил на эту ось:
.
Тогда задача сведется к движению материальной точки под действием одной силы . При этом уравнение движения примет наиболее простой вид:
(2) .
В дальнейшем, проекцию равнодействующей мы будем называть просто силой, действующей на точку.
Сила может быть как постоянной, так и зависеть от времени t , координаты x и от скорости . К сожалению, если зависит от всех перечисленных факторов, то не всегда возможно решить уравнение (2) аналитически. Поэтому мы рассмотрим те случаи, когда возможно получить аналитическое решение этого уравнения. Заметим, что если сила является постоянной, то уравнение (2) можно решать любыми, приводимыми ниже, способами.
Почему мы обозначаем в виде проекции силы на ось x , хотя рассматриваем только движение вдоль одной оси? – Потому что под обозначением силы R в виде одной буквы, часто подразумевается ее абсолютная величина: . Она имеет неотрицательные значения: . А когда мы пишем силу как проекцию , то подразумеваем, что эта величина может быть как положительной (если сила направлена вдоль оси x ), так и отрицательной (когда она направлена противоположно оси x ). В теоретической механике, в подобных случаях, иногда также говорят, что есть алгебраическое значение силы. Это относится не только к силе, ни и ко всем другим, рассматриваемым далее, векторным величинам.
Интегрирование уравнения движения с силой, зависящей от времени
Вначале рассмотрим случай, когда задан закон изменения силы со временем: . Перепишем уравнение (2), явно указав эту зависимость:
(t1) .
В этом уравнении время t является независимой переменной; координата x – зависимой переменной; – это вторая производная координаты по времени: . Масса m – это постоянная, то есть заданное число. С математической точки зрения, уравнение (t1) есть дифференциальное уравнение второго порядка, не содержащую зависимую переменную x в явном виде.
Решение такого уравнения выполняется с помощью подстановки
.
Тогда
.
Подставляя в (t1), мы получаем дифференциальное уравнение первого порядка:
(t2) .
Выполняя подстановку, мы ввели новую переменную , равную производной координаты x по времени t . Эта производная является проекцией скорости точки на ось Ox . Таким образом, процесс решения разбивается на две части. Сначала мы, решаем уравнение (t2), и находим закон изменения скорости со временем: . Затем, используя уравнение , находим закон изменения координаты .
Упростим уравнение (t2), разделив его на массу m :
(t3) ,
где – ускорение точки. Поскольку зависимость силы от времени известна, то и зависимость ускорения от времени также известна.
Уравнение (t3) является дифференциальным уравнением первого порядка с разделяющимися переменными. Разделяем переменные и интегрируем.
;
(t4) ;
(t5) .
Здесь – постоянная интегрирования. Чтобы ее определить, нужно знать значение скорости в какой-либо момент времени . Если мы сможем выразить интеграл через известные функции, то подставив в (t5) значения времени и значение скорости в этот момент, мы сможем определить постоянную .
Для простых задач, формула (t5) вполне удобна. Но если интеграл не выражается через известные функции, то выполнить численное интегрирование по этой формуле нельзя. Поэтому найдем закон изменения скорости со временем в более удобном виде.
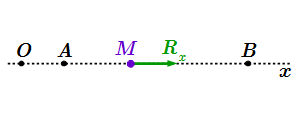
Прямолинейное движение точки M под действием силы Rx.
Пусть нам известно, что в момент времени , точка M находилась в положении A, имела координату и скорость . Рассмотрим произвольный момент времени . Пусть в этот момент времени точка M находится в положении B, с координатой и скоростью . Величины и нам пока не известны. Наша задача их найти.
Перепишем (t4) явно указав, что есть функция от t :
(t6) .
Интегрируем (t6) от момента времени до :
.
Слева – интеграл от полного дифференциала. Поэтому он интегрируется элементарно:
.
Здесь мы учли, что . В результате получаем:
;
.
Этот результат можно получить и несколько иначе, если в интеграле сразу перейти к переменной . Тогда пределы интегрирования станут и . В результате получим тоже самое:
.
Итак, мы нашли значение скорости в произвольный момент времени :
(t7) .
Заменим обозначение момента времени на t . В результате получим закон изменения скорости со временем t :
(t8) .
Интеграл справа записан не вполне корректно, хотя так часто пишут. Рассмотрим пример определенного интеграла . Он зависит от пределов интегрирования a и b , но не зависит от переменной интегрирования t . Можно сказать, что переменная t принимает заданные значения из отрезка , которые применяются только для вычисления интеграла. Поэтому для переменной интегрирования t можно использовать любое обозначение. Например, можно использовать переменную . Тогда .
В (t8) мы использовали одно и то же обозначение, как для верхнего предела интеграла, так и для переменной интегрирования. Это может привести к путанице. Поэтому используем для переменной интегрирования любое другое, не используемое обозначение, например . Тогда формула (t8) примет следующий вид:
(t9) .
Теперь найдем закон изменения координаты x от времени. Интегрируем уравнение
.
Разделяем переменные:
(t10) .
Здесь мы также можем выполнить интегрирование от A до B, но мы продемонстрируем другой способ, как получить результат в удобном виде, применяя неопределенный интеграл. Поскольку неопределенный интеграл определен с точностью до постоянной, то запишем его с нижним пределом интегрирования . Интегрируем (t10):
(t11) .
Найдем значение постоянной интегрирования . Для этого подставим сюда :
.
Далее учитываем, что значение координаты точки в момент времени нам известно: . Также учитываем, что интеграл в правой части имеет равные пределы интегрирования и поэтому равен нулю. В результате получаем:
.
Отсюда находим значение постоянной интегрирования: . В результате получаем закон движения точки:
(t12) .
Итак, мы нашли, что если на точку действует сила , то для определения ее закона движения, нужно сначала определить закон изменения скорости со временем:
(t7) .
А затем определить закон движения:
(t12) .
При этом мы полагаем, что нам известны скорость и координата в некоторый момент времени . Если бы мы проводили интегрирование через неопределенные интегралы в общем виде, то и были бы постоянными интегрирования и .
Постоянная сила
Разберем случай, когда действующая на точку сила имеет постоянное значение: . В этом случае ускорение также постоянно: . Интегрируем, используя таблицу неопределенных интегралов. Из (t7) находим закон изменения скорости со временем:
;
(t14) .
Мы видим, что скорость линейно изменяется со временем.
Подставляем в (t12) и находим закон движения точки:
;
(t15) .
Если в начальный момент времени , скорость точки была , а координата , то . Из (t14) и (t15) получаем:
;
.
Равномерное движение
Если проекция силы на ось Ox равна нулю: , то ускорение также равно нулю: . В этом случае из (t14) находим, что скорость точки постоянна:
.
Из (t15) находим, что координата линейно меняется со временем:
.
Если в начальный момент времени , скорость точки была , а координата , то ;
;
.
Интегрирование уравнения движения с силой, зависящей от скорости
Разберем случай прямолинейного движения материальной точки, когда действующая сила зависит от скорости . Такие задачи встречаются при движении в жидкой или газообразной среде, когда на точку помимо постоянных сил, действует сила трения, зависящая от скорости. В этом случае, уравнение движения имеет вид:
(v1) .
Разделим обе части уравнения на массу m :
(v2) ,
где – ускорение точки. Теперь нам известна зависимость ускорения точки от ее скорости. Уравнение (v2) не содержит в явном виде как зависимую переменную x , так и независимую переменную t . Поэтому его можно решать двумя способами.
Решение уравнения, определяя vx(t)
Применим к уравнению (v2) метод решения дифференциального уравнения, не содержащего зависимую переменную в явном виде. Для этого, как и в предыдущем случае, делаем подстановку
.
Тогда
.
Подставляя в (v2), мы получаем дифференциальное уравнение первого порядка:
(v3) .
Пусть, как и в предыдущем случае, в момент времени , точка находилась в положении A, имела координату и скорость . И пусть в произвольный момент времени , точка находится в положении B с координатой и скоростью . Нам нужно найти величины и .
Разделяем переменные.
;
.
Перепишем это уравнение, указав, что скорость является функцией от времени:
.
Интегрируем по времени от до :
.
В левой части сделаем замену переменной. От переменной t перейдем к переменной . При этом изменим пределы интегрирования учитывая, что при ; и при :
(v4) .
Заменим обозначения переменных , и переменной интегрирования . Подставим в (v4):
(v5) .
Это уравнение, в неявном виде, дает закон изменения скорости от времени t . Вычислив интеграл, и выполнив преобразование, мы можем выразить через t : .
Далее, по формуле (t12) ⇑ определяем закон движения материальной точки:
(t12) .
Решение уравнения, определяя vx(x)
Выпишем уравнение (v2) еще раз.
(v2) .
Для применения этого метода, в качестве независимой переменной возьмем координату x , а в качестве зависимой – скорость . То есть считаем, что скорость является функцией от координаты: .
Выразим через переменные x и вторую производную координаты по времени:
.
Подставим в (v2) и разделяем переменные:
;
.
В левой части в явном виде запишем как функцию от x , и интегрируем по x от положения A до B:
;
.
В интеграле слева переходим от переменной x к :
(v6) .
Переобозначим переменные:
(v7) .
Это уравнение дает в неявном виде зависимость скорости от координаты:
.
Подставив сюда , получим для x дифференциальное уравнение первого порядка. Решаем его методом разделения переменных:
;
.
Интегрируем от положения A до B:
;
.
Заменим переменные:
(v8) .
Уравнение (v8) дает в неявном виде закон движения материальной точки .
Интегрирование уравнения движения с силой, зависящей от перемещения
Наконец рассмотрим случай прямолинейного движения материальной точки, когда действующая сила зависит от перемещения x . Такие задачи встречаются при движении в потенциальных полях – в гравитационных или электрических. Сюда также относится движение груза, прикрепленного к упругой пружине.
Выписываем уравнение движения для этого случая:
(x1) .
Это дифференциальное уравнение второго порядка. Оно не содержит независимую переменную t в явном виде. Также как и в предыдущем случае, применяем метод решения дифференциального уравнения, не содержащего независимую переменную в явном виде.
Перейдем к новым переменным. В качестве независимой переменной возьмем координату x , а в качестве зависимой – скорость . Считаем, что скорость является функцией от координаты: .
Выразим вторую производную координаты по времени через переменные x и :
;
Подставим в (x1) и разделяем переменные:
(x2) ;
.
Интегрируем по x от A до B:
(x3) .
Вычисляем интеграл, используя таблицу неопределенных интегралов:
;
.
Подставляем в (x3):
(x4) . Нетрудно видеть, что слева стоит изменение кинетической энергии материальной точки. Справа – работа, которую совершает сила при перемещении материальной точки из A в B. Само уравнение (x4) представляет собой теорему об изменении кинетической энергии точки для прямолинейного движения.
Вернемся снова к уравнению (x2).
(x2) .
Его можно проинтегрировать и другим способом.
Для этого представим правую часть в виде производной по координате:
,
где – координата произвольной заранее выбранной точки C .
Левую часть также представим в виде производной по координате:
.
Тогда (x2) можно записать в виде:
.
Поскольку производная по x от выражения в скобках равна нулю, то само выражение является постоянной, не зависящей от x величиной:
.
Такая форма записи, когда некоторая функция от переменных приравнивается постоянной, называется интегралом дифференциального уравнения. Перепишем его в следующем виде:
(x5) .
Здесь – кинетическая энергия точки; – потенциальная энергия, отсчитываемая от, произвольным образом выбранной, точки C ; E – постоянная интегрирования, которая в данном случае имеет определенный физический смысл – это полная механическая энергия материальной точки. Поэтому мы ее обозначили привычной для этого случая буквой E . Само уравнение (x5) представляет собой закон сохранения механической энергии. С математической точки зрения, энергия E является интегралом дифференциального уравнения, или, как говорят в механике, интегралом движения точки. То есть величиной, сохраняющей при движении постоянное значение.
Выше мы пришли к выводу, что постоянная интегрирования E не зависит от координаты x , но ничего не сказали о ее зависимости от времени. Однако, для одномерного движения, со временем может изменяться только одна координата x . Поскольку постоянная E от нее не зависит, то она не зависит также и от времени t . Поэтому полная механическая энергия сохраняет постоянное значение и в различные моменты времени.
Нетрудно видеть, что формулировки (x4) ⇑ и (x5) ⇑ эквивалентны. Для доказательства, приравняем механическую энергию точки для двух положений A и B:
;
.
Здесь мы разбили интеграл от до на два интеграла – от до ; и от до . Интегралы от до сократились.
Найдем зависимость скорости точки от координаты. При этом мы считаем, что скорость точки в положении A нам известна. Рассмотрим два положения: A и B. Из (x4) ⇑ имеем:
,
где – работа, которая производит сила при перемещении точки из A в B. Наконец, заменим на x , и на . В результате получим искомую зависимость:
(x6) ,
где – работа, которая производит сила при перемещении материальной точки из A в точку с координатой x . Скорость определена с точностью до знака (плюс или минус). Знак нужно выбирать из начальных условий и исследования движения. Если в точке , то при достаточно малых значениях . Далее точка может остановиться и начать движение в обратную сторону. Тогда нужно выбрать знак минус, чтобы скорость стала отрицательной.
Теперь, зная зависимость , находим закон движения материальной точки. Для этого интегрируем уравнение:
;
;
;
.
Это уравнение дает в неявном виде зависимость координаты x от времени t .
Приложение к движению в пространстве
Приведенные выше результаты могут быть применимы и для некоторых случаев движения материальной точки в двухмерном или трехмерном пространстве.
Пусть нам известно, что в момент времени , материальная точка находилась в точке A, и имела скорость . Выберем трехмерную систему координат Oxyz , и распишем эти начальные условия по компонентам:
При ;
При ;
При .
Сила в пространстве, зависящая от времени
Пусть на материальную точку действует сила, зависящая от времени: . Составим уравнения ее движения:
.
Выпишем уравнение для координаты x с начальными условиями:
; при .
Здесь все необходимые величины известны, и они не зависят от значений других координат. Мы можем найти закон изменения координаты x со временем, применяя интегрирование уравнения движения с силой, зависящей от времени ⇑ для прямолинейного движения.
Выпишем уравнение для координаты y с начальными условиями:
; при .
Здесь также известны все необходимые величины, и они не зависят от значений других координат. Мы также можем найти закон изменения координаты y со временем, применяя интегрирование, как для прямолинейного движения.
Точно также мы можем найти закон изменения координаты z со временем. В этом случае говорят, что переменные разделились. Уравнения движения, составленные для каждой из координат, вместе с начальными условиями, не зависят от значений других координат. Поэтому каждое такое уравнение можно проинтегрировать отдельно. В результате мы получим закон движения материальной точки в трехмерном случае: .
Силы, приводящие к разделению переменных
Пусть теперь на точку действуют три взаимно перпендикулярные силы. И пусть одна из них зависит только от времени; вторая – от проекции скорости на направление силы; третья – от проекции радиус-вектора на направление силы.
Выберем систему координат Oxyz , оси которой направим вдоль направлений действующих сил. Тогда в этой системе координат отличными от нуля будут только три проекции сил: . Составляем уравнения движения:
;
;
.
Мы видим, что и в этом случае переменные разделились. Каждое из этих уравнений зависит только от одной переменной. И мы можем решить его, применяя изложенные выше методы. Все это применимо и к случаю, когда любая из этих сил является постоянной.
И, разумеется, тут могут быть различные вариации, приводящие к разделению переменных. Например, если зависящая от времени сила лежит в плоскости xy , а перпендикулярная ей сила зависит только от координаты z . В этом случае переменные также разделяются.
Автор: Олег Одинцов . Опубликовано: 12-10-2020
http://www.evkova.org/pryamolinejnoe-dvizhenie-tochki-v-teoreticheskoj-mehanike
http://1cov-edu.ru/mehanika/dinamika-tochki/pryamolinejnoe-dvizhenie/