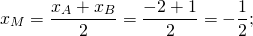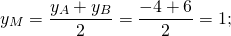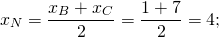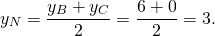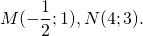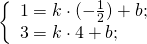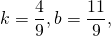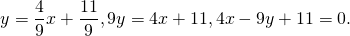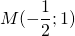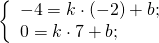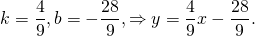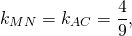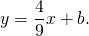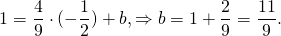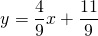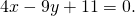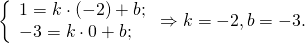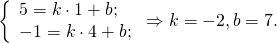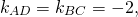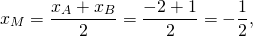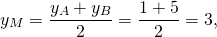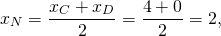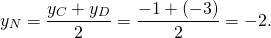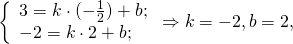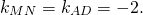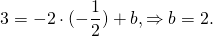Уравнение прямой an треугольнике параллельна стороне bc

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Уравнение средней линии

Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?

Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.

Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.

1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.

М — середина отрезка AB, N — середина BC.

Составим уравнение прямой MN, например, в виде y=kx+b:

Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.

— середина отрезка AB. Составим уравнение прямой AC:

Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.

Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:

то есть уравнение прямой MN ищем в виде

Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:

Таким образом, уравнение прямой MN

Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.

Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).

Сначала следует определить основания данной трапеции.

Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.

Значит, уравнение прямой AD: y= -2k-3.
B(1;5), C(4;-1),

Уравнение прямой BC: y= -2k+7.

Поскольку угловые коэффициенты прямых равны:

то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины AB и CD соответственно.

Составим уравнение прямой MN, M(-1/2;3), N(2;-2):

Уравнение AD — y= -2k-3, середина AB — M(-1/2;3). Составляем уравнение прямой MN, параллельной прямой AD.

Значит уравнение MN ищем в виде y= -2x+b.

Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:

Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.

Задача 31020 [b]1.[/b] Треугольник задан вершинами .

Условие

[b]1.[/b] Треугольник задан вершинами :

Найти:
1. Уравнение прямой AM, параллельной стороне ВС;

2. Уравнение медианы AD, ее длину;

3. Уравнение высоты BF;

4. Центр тяжести треугольника;

6. Площадь треугольника

[b]2.[/b] Найти расстояние между центрами окружностей и линию центров этих окружностей:

x^2+y^2-4x-2y-15 = 0
x^2+y^2+6x+18y-55 = 0

Все решения

2.
Выделим полные квадраты:
(x^2-4x)+(y^2-2y)-15=0
(x-2)^2+(y-1)^2=10
центр окружности O(2;1)

(x^2+6x)+y^2+18y)-55=0
(x+3)^2+(y+9)^2=155
центр окружности O_(1)(-3;-9)

1.
1)Уравнение прямой проходящей через точкy (x_(o);y_(o)) с направляющим вектором vector =(p;q) имеет вид
(x-x_(o))/p=(y-y_(o))/q

Уравнение прямой АМ как прямой проходящей через точкy А(-2;-2) с направляющим вектором vector =(1-7;2-(-6))=(-6;8)

2) Координаты точки D — середины BC
x_(D)=(x_(B)+x_(C))/2 = (7+1)/2=4
y_(D)=(y_(B)+y_(C))/2= (-6+2)/2)=-2
[b]D(4;-2)[/b]
По условию
[b]А(-2;-2)[/b]

Значит,
[b]уравнение медианы AD:
y=-2[/b]

3)
Высота BF перпендикулярна прямой AC.

Уравнение прямой АС как прямой, проходящей через две точки:
(x-(-2))/(1-(-2))=(y-(-2))/(2-(-2)) ⇒ (x+2)/(3)=(y+2)/4 ⇒
4х — 3у +2=0
y=(4/3)x+(2/3)
k_(AC)=4/3

Общий вид прямых, перпендикулярных АС:
у=(-3/4)х + m

Подставим координаты точки В
-6 = (-3/4)*7 + m
m=-3/4

4) Центр тяжести треугольника — точка пересечения медиан.
Составим уравнение медианы ВК.
К — середина АС
К((-2+1)/2;(-2+2)/2)=К(-1/2; 0)

Точка пересечения медианы АМ и медианы ВК:
y=-2
4x=8
x=2

Уравнение средней линии

Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?

Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.

Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.

1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.

М — середина отрезка AB, N — середина BC.

Составим уравнение прямой MN, например, в виде y=kx+b:

Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.

— середина отрезка AB. Составим уравнение прямой AC:

Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.

Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:

то есть уравнение прямой MN ищем в виде

Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:

Таким образом, уравнение прямой MN

Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.

Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).

Сначала следует определить основания данной трапеции.

Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.

Значит, уравнение прямой AD: y= -2k-3.
B(1;5), C(4;-1),

Уравнение прямой BC: y= -2k+7.

Поскольку угловые коэффициенты прямых равны:

то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины AB и CD соответственно.

Составим уравнение прямой MN, M(-1/2;3), N(2;-2):

Уравнение AD — y= -2k-3, середина AB — M(-1/2;3). Составляем уравнение прямой MN, параллельной прямой AD.

Значит уравнение MN ищем в виде y= -2x+b.

Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:

Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.