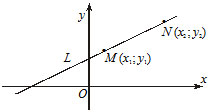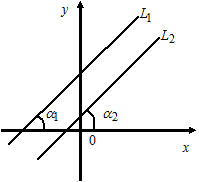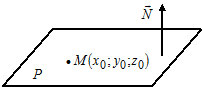Уравнение прямой bn параллельной ac
Даны координаты вершины треугольника АВС: А (6; -2); В (1;2); С(3;5).Найдите: 1. Уравнение прямой BN, параллельной стороне АС;
Уравнение прямой, проходящей через точки А и С:
Так как А (6; -2) и С(3;5), получим
Параллельные прямые имеют одинаковые угловые коэффициенты
Уравнение прямой, параллельной АС имеет вид
Для нахождения коэффициента b подставим координаты точки В (1;2)
Уравнение прямой bn параллельной ac
Вопрос по алгебре:
Даны координаты вершины треугольника АВС: А (-6; -2); В (4; 8); С(2; -8).
Найдите:
1. Уравнение прямой BN, параллельной стороне АС;
2. Уравнение медианы CD;
3. Уравнение высоты АЕ;
4. Угол В;
5. Центр тяжести треугольника.
Помогите, пожалуйста, или хотя бы частично .__.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 2
Смотри ответ во вложении
1) BN (x-4;у-8), AC (8;-6).
Так как они параллельны, то уравнение BN имеет вид:
х-4/8=y-8/-6.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
- Высшая математика.
- Аналитическая геометрия.
Аналитическая геометрия.
Прямая на плоскости, всевозможные уравнения.
Прямая на плоскости, всевозможные уравнения.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Существуют такие формы записи уравнения прямой:
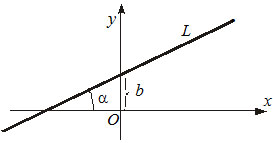
1) $y=kx+b,$ где $k -$ угловой коэффициент, $b-$ отрезок, который прямая отсекает на оси $OY.$
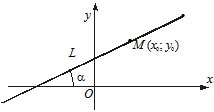
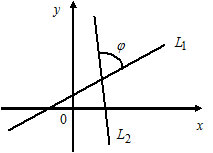
2) $y-y_0=k(x-x_0) $ — уравнение прямой, которая проходит через заданную точку $P(x_0, y_0)$ под заданным углом $\alpha$ к оси $OX$ $(k=tg\alpha).$
3) $\frac =\frac $ — уравнение прямой, которая проходит через две точки $M(x_1, y_1)$ и $N(x_2, y_2).$
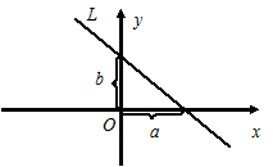
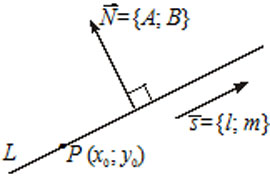
5) $\frac =\frac $ — каноническое уравнение прямой, где $\overline =(l, m) -$ направляющий вектор прямой, то есть вектор параллельный прямой $(\overline \parallel L),$ точка $P(x_0, y_0)\in L.$
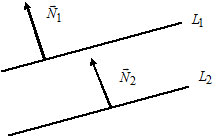
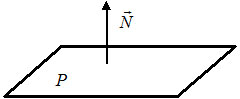
6) $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $\overline =(A, B).$ Вектор $\overline N$ называется нормальным вектором прямой.
7) $Ax+By+C=0 -$ общее уравнение прямой $L,$ где $\overline =(A, B) -$ нормальный вектор прямой $L.$
8) $x\cos\alpha+y\cos\beta-p=0 -$ нормальное уравнение прямой, где $\cos\alpha$ и $\cos\beta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.
Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac .$
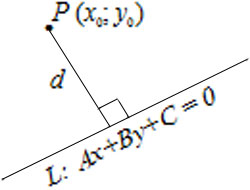
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=\left|\frac \right|.$$
Расположение двух прямых на плоскости.
Условия параллельности двух прямых:
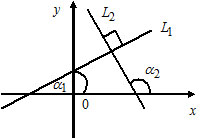
1) Пусть $L_1: k_1x+b_1,$ $k_1=tg\alpha_1;$
$L_2: k_2x+b_2,$ $k_2=tg\alpha_2.$
Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $k_1=k_2.$
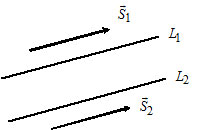
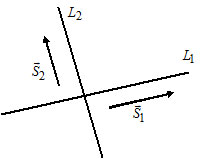
2) Пусть $L_1:$ $\frac =\frac ,$ $\overline _1=(l_1, m_1);$
Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $\overline _1\parallel\overline _2\Leftrightarrow$ $\frac =\frac .$
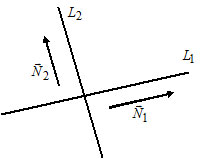
3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $\overline _1=(A_1, B_1);$
$L_2: A_2x+B_2y+C_2=0,$ $\overline _2=(A_2, B_2).$
Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $\overline _1\parallel\overline _2\Leftrightarrow$ $\frac=\frac .$
Условия перпендикулярности двух прямых:
1) Пусть $L_1: k_1x+b_1,$ $k_1=tg\alpha_1;$
$L_2: k_2x+b_2,$ $k_2=tg\alpha_2.$
$L_1\perp L_2\Leftrightarrow$ $k_1\cdot k_2=-1.$
2) Пусть $L_1:$ $\frac =\frac ,$ $\overline _1=(l_1, m_1);$
$L_1\perp L_2\Leftrightarrow$ $\overline _1\perp\overline _2\Leftrightarrow$ $ \cdot + \cdot =0.$
3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $\overline _1=(A_1, B_1);$
$L_2: A_2x+B_2y+C_2=0,$ $\overline _2=(A_2, B_2).$
$L_1\perp L_2\Leftrightarrow$ $\overline _1\perp\overline _2\Leftrightarrow$ $\cdot+ \cdot =0.$
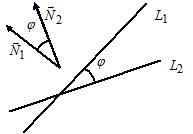
Угол между прямыми:
1) Пусть $L_1: k_1x+b_1,$ $k_1=tg\alpha_1;$
$L_2: k_2x+b_2,$ $k_2=tg\alpha_2.$
2) Пусть $L_1:$ $\frac =\frac ,$ $\overline _1=(l_1, m_1);$
3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $\overline _1=(A_1, B_1);$
$L_2: A_2x+B_2y+C_2=0,$ $\overline _2=(A_2, B_2).$
Примеры:
2.141.
а) Прямая $L$ задана точкой $M_0(-1; 2)\in L$ и нормальным вектором $\overline N(2; 2).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.
Решение.
Подставим в формулу 6) для уравнения прямых ( $A(x-x_0)+B(y-y_0)=0$ ) соответственно координаты точки $(x_0; y_0)=M_0(-1; 2)$ и вектора $(A; B)=\overline N(2; 2):$
$2(x+1)+2(y-2)=0.$ Далее, приведем это уравнение к общему виду:
Нормальное уравнение прямой имеет вид $x\cos\alpha+y\cos\beta-p=0,$ где $\cos\alpha$ и $\cos\beta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.
Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac .$
Для нашей прямой имеем $A=1; B=1; C=-1 \Rightarrow sgn C=-1.$ Таким образом, $\mu=-\frac >=\frac .$
Запишем нормальное уравнение прямой:
Расстояние от начала координат $p=\frac .$
Ответ: $2(x+1)+2(y-2)=0;$ общее уравнение $x+y-1=0;$ нормальное уравнение прямой $\frac x+\frac y-\frac =0;$ $p=\frac .$
2.142.
а) Прямая $L$ задана точкой $M_0(-1; 2)\in L$ и направляющим вектором $\overline S(3; -1).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.
Решение.
Подставим в формулу 5) для уравнения прямых ( $\frac =\frac $ ) соответственно координаты точки $(x_0; y_0)=M_0(-1; 2)$ и вектора $(l; m)=\overline S(3; -1):$ $\frac =\frac $
Далее, приведем это уравнение к общему виду:
Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac .$
Для нашей прямой имеем $A=1; B=3; C=-5 \Rightarrow sgn C=-1.$ Таким образом, $\mu=-\frac >=\frac >.$
Запишем нормальное уравнение прямой:
Расстояние от начала координат $p=\frac >.$
Ответ: $\frac =\frac ;$ общее уравнение $x+3y-5=0;$ нормальное уравнение прямой $\frac >x+\frac >y-\frac >=0;$ $p=\frac >.$
2.143.
а) Прямая $L$ задана двумя своими точками $M_1(1; 2)\in L$ и $M_2(-1; 0)\in L.$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.
Решение.
Подставим в формулу 3) для уравнения прямых ($\frac =\frac $ ) соответственно координаты точек $M_1(1; 2)= (x_1; y_1) $ и $M_2(-1; 0)=(x_2; y_2):$ $\frac =\frac \Rightarrow \frac =\frac .$
Далее, приведем это уравнение к общему виду:
Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac .$
Для нашей прямой имеем $A=1; B=-1; C=1 \Rightarrow sgn C=1.$ Таким образом, $\mu=-\frac >=-\frac >.$
Запишем нормальное уравнение прямой:
Расстояние от начала координат $p=\frac >.$
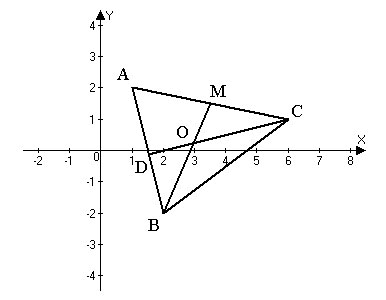
2.150. Треугольник $ABC$ задан координатами своих вершин $A(1; 2), B(2; -2), C(6; 1).$ Требуется:
1) Найти уравнение стороны $AB;$
2) найти уравнение высоты $CD$ и вычислить ее длину $h=|CD|;$
3) найти угол между высотой $CD$ и медианой $BM.$
Решение.
1) Уравнение прямой $AB$ найдем по формуле уравнения прямой, проходящей через две точки $\frac =\frac . $
В нашем случае $(x_1; y_1)=A(1; 2);$ $(x_2; y_2)=B(2; -2).$
Подставляем координаты точек в уравнение прямой. Получаем $$\frac =\frac \Rightarrow x-1=\frac .$$ Запишем общее уравнение прямой $AB$:
$-4(x-1)=y-2\Rightarrow$ $-4x+4=y-2\Rightarrow$ $4x+y-6=0.$
2) Уравнение прямой $CD$ найдем, пользуясь уравнением ( 6): $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $\overline =(A, B).$
В нашем случае, высота $CD$ это прямая, которая проходит через точку $C$ перпендикулярно вектору $AB.$
Таким образом, $$(x_0; y_0)=C=(6; 1);\quad\overline =\overline=(2-1; -2-2)=(1; -4).$$
Подставляем эти координаты в уравнение прямой:
$1(x-6)-4(y-1)=0\Rightarrow x-6-4y+4=0 \Rightarrow x-4y-2=0.$
То есть, уравнение прямой $CD:$ $x-4y-2=0.$
Чтобы найти длину высоты $h=|CD|,$ найдем координаты точки $D,$ как точки пересечения прямых $CD$ и $AB:$
Решим систему методом исключений:
Следовательно имеем $D(26/17; -2/17).$ Теперь можем найти длину высоты $CD:$
3) Уравнение высоты $CD$ мы уже нашли в пункте 2). Найдем уравнение медианы $BM.$ Будем его искать, используя форумулу уравнения прямой, проходящей через две точки.
Координаты точки $B=(2, -2); $ координаты точки $M$ найдем как середину стороны $AC:$ $x_M=\frac ; y_M=\frac .$
Подставляем координаты точек $B(2; -2)$ и $M(3.5; 1.5)$ в уравнение прямой
$3.5(x-2)=1.5(y+2)\Rightarrow 3.5x-7=1.5y+3 \Rightarrow 3.5x-1.5y-10=0.$
Далее, зная общие уравнения двух прямых $CD: x-4y-2=0$ и $BM: 3.5x-1.5y-10=0$ можно найти угол между ними по формуле
где $L_1: A_1x+B_1y+C_1=0,$ $\overline _1=(A_1, B_1);$
$L_2: A_2x+B_2y+C_2=0,$ $\overline _2=(A_2, B_2).$
Для наших прямых имеем: $(A_1, B_1)=(1; -4);$ $(A_2; B_2)=(3.5; -1.5).$
Ответ: 1) $AB: 4x+y-6=0.$
2.160. В равнобедренном треугольнике $ABC$ заданы вершина $C(4; 3),$ уравнение $2x-y-5=0$ основания $AC$ и уравнение $x-y=0$ боковой стороны $AB.$ Найти уравнение стороны $BC.$
Решение.
Найдем координаты вершины треугольника $A,$ как точки пересечения прямых $AB$ и $AC:$
Таким образом, мы имеем координаты вершин при основании равнобедренного треугольника $A(5; 5)$ и $C(4; 3).$ Найдем координаты вершины $B(x, y).$ Мы знаем, что эта точка принадлежит прямой $AB: x-y=0$ и что $AB=BC.$ Запишем формулы для длин сторон $AB$ и $BC:$
Далее, чтобы найти координаты точки $B,$ решим систему уравнений:
Зная координаты точек $B$ и $C$ можно записать уравнение прямой $BC,$ как прямой проходящей через две точки $\left(\frac =\frac \right):$
$$\Rightarrow\frac =\frac \Rightarrow 7x-28=y-3\Rightarrow 7x-y-25=0.$$
Ответ: $7x-y-25=0.$
2.165. Даны две противоположные вершины квадрата $A(1; 3)$ и $C(-1; 1).$ Найти координаты двух его других вершин и написать уравнения его сторон.
Решение:
Найдем уравнение диагонали $AC:$
Далее, найдем уравнение второй диагонали квадрата — прямой, проходящей через точку $O$ перпендикулярно прямой $AC.$ Для прямой $AC$ нормальный вектор имеет координаты $\overline =(1; -1).$ Прямая, перпендикулярная прямой $AC$ является параллельной нормальному вектору $\overline $. Таким образом, уравнение прямой $BD$ запишем по формуле 5) $\left(\frac =\frac \right),$ где $(x_0, y_0)=O(0; 2),$ $(l, m)=\overline =(1, -1):$
$$\frac =\frac \Rightarrow x=-y+2 \Rightarrow x+y-2=0.$$
Ясно, что $AO=CO=BO=DO.$ Найдем длину отрезка $AO:$ $AO=\sqrt =\sqrt .$
Далее, будем искать координаты точек $B$ и $D,$ принадлежащих прямой $BD$ и таких, что $BO=DO=AO.$
Таким образом, мы нашли координаты вершин $B(1; 1)$ и $D(-1; 3).$ Зная координаты вершин квадрата, запишем уравнения его сторон, пользуясь формулой ( 3) — $\frac =\frac $ — уравнение прямой, которая проходит через две точки $M(x_1, y_1)$ и $N(x_2, y_2).$
Ответ: $A(1; 3),$ $B(1; 1),$ $C(-1; 1),$ $D(-1; 3);$ $AB:$ $x=1;$ $BC:$ $y=1;$ $CD:$ $x=-1;$ $DA:$ $y=3.$
Деление отрезка в заданном отношении (векторный и координатный способы).
Деление отрезка в заданном отношении (векторный и координатный способы).
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $\lambda,$ в котором точка $M$ делит направленный отрезок $\overline ,$ найдем координаты точки $M.$
Пусть $O -$ начало координат. Обозначим $\overline =r_1,$ $\overline =r_2,$ $\overline =r.$ Так как, $$\overline =r-r_1, \overline =r_2-r,$$ то $r-r_1=\lambda(r_2-r),$ откуда (так как $\lambda\neq -1$) $$r=\frac .$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=\frac , y=\frac , z=\frac .$$
Примеры.
2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.
Решение.
Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$\lambda_1=\frac =\frac ;$$ $$x_C=\frac =\frac \cdot 6> >=4;$$
Далее находим координаты точки $D:$
Ответ: $(4, 0)$ и $(5, 2).$
2.58. Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.
Решение.
Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.
Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:
Аналогичные равенства запишем для точки $D:$
Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$ и $z_A, z_B$ попарно в виде систем и решим их:
Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$
Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$
Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.
Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Существуют такие формы записи уравнения плоскости:
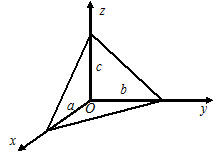
1) $Ax+By+Cz+D=0 -$ общее уравнение плоскости $P,$ где $\overline =(A, B, C) -$ нормальный вектор плоскости $P.$
2) $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости $P,$ которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $\overline =(A, B, C).$ Вектор $\overline N$ называется нормальным вектором плоскости.
4) $\begin x-x_1&y-y_1&z-z_1\\x_2-x_1&y_2-y_1&z_2-z_1\\x_3-x_1&x_2-x_1&x_3-x_1\end =0 — $ уравнение плоскости, которая проходит через три точки $A(x_1, y_1, z_1), B(x_2, y_2, z_2)$ и $C(x_3, y_3, z_3).$
5) $x\cos\alpha+y\cos\beta+z\cos\gamma-p=0 -$ нормальное уравнение плоскости, где $\cos\alpha, \cos\beta$ и $\cos\gamma -$ направляющие косинусы нормального вектора $\overline ,$ направленного из начала координат в сторону плоскости, а $p>0 -$ расстояние от начала координат до плоскости.
Общее уравнение плоскости приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac .$
Расстояние от точки $M(x_0, y_0, z_0)$ до плоскости $P: Ax+By+Cz+D=0$ вычисляется по формуле $$d=\left|\frac \right|.$$
Примеры:
2.180.
а) Заданы плоскость $P: -2x+y-z+1=0$ и точка $M(1, 1, 1).$ Написать уравнение плоскости $P’,$ проходящей через точку $M$ параллельно плоскости $P$ и вычислить расстояние $\rho(P, P’).$
Решение.
Так как п.лоскости $P$ и $P’$ параллельны, то нормальный вектор для плоскости $P$ будет также нормальным вектором для плоскости $P’.$ Из уравнения плоскости получаем $\overline =(-2, 1, -1).$
Далее запишем уравнение плоскости по формуле ( 2): $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости, которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $\overline =(A, B, C).$
Ответ: $-2x+y-z+2=0.$
2.181.
а) Написать уравнение плоскости $P’,$ проходящей через заданные точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ перпендикулярно заданной плоскости $P: -x+y-1=0.$
Решение.
Из уравнения плоскости $P,$ находим ее нормальный вектор $\overline =(-1, 1, 0).$ Плоскость, перпендикулярная плоскости $P,$ параллельна ее нормальному вектору. Отсюда следует, что можно выбрать точку $M_3(x, y, z)\in P’$ такую, что что $\overline ||\overline .$
Поскольку $z_N=0,$ то есть вектор $N\in XoY,$ то $z_ =0.$
Мы нашли точку $M_3=(2, 1, 0).$
Так как точка $M_1\in P’,$ то и $M_3\in P’.$ Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(2, 1, 0).$
$(x-1)(-1)0+(-1)z+(y-2)-(-1)z-(-1)(x-1)-(y-2)0=0\Rightarrow$ $\Rightarrow-z+y-2+z+x-1=0\Rightarrow x+y-3=0.$
2.182.
а) Написать уравнение плоскости $P,$ проходящей через точку $M(1, 1, 1)$ параллельно векторам $a_1(0, 1, 2)$ и $a_2(-1, 0, 1).$
Решение.
Поскольку вектор $[a_1, a_2]$ перпендикулярен плоскости векторов $a_1$ и $a_2$ (см. векторное произведение), то он будет также перпендикулярен искомой плоскости. То есть вектор $[a_1, a_2]$ является нормальным для плоскости $P.$ Найдем этот вектор:
Таким образом $\overline =[a_1, a_2]=(1, -2, 1).$
Теперь можно найти уравнение плоскости $P,$ по формуле (2), как плоскости, проходящей через точку $M(1, 1, 1)$ перпендикулярно вектору $\overline N=(1, -2, 1):$
Ответ: $x-2y+z=0.$
2.183.
а) Написать уравнение плоскости $P,$ проходящей через точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ параллельно вектору $a=(3, 0, 1).$
Решение.
Поскольку вектор $a$ параллелен плоскости $P,$ то для всякого вектора $\overline ,$ параллельного вектору $a,$ точка $M_3\in P.$
Пусть $M_3=(x, y, z).$ Тогда $\overline =(x-1, y-2, z).$ Так как $\overline ||a,$ то $\frac > =\frac > =\frac > .$ $y_a=0,$ то есть вектор $a\in XoZ$ и всякий параллельный ему вектор так же будет принадлежать этой плоскости. Таким образом, $y_ =y-2=0\Rightarrow y=2.$
Из условия параллельности векторов имеем $\frac =\frac .$ Пусть $x=4,$ тогда $z=1.$
Мы получили точку $M_3=(4, 2, 1).$
Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(4, 2, 1).$
$(x-1)(-1)1+1\cdot z\cdot 0+(y-2)3-3(-1)z-0\cdot 1\cdot(x-1)-1(y-2)1=0\Rightarrow$
$\Rightarrow -x+1+3y-6+3z-y+2=0\Rightarrow -x+2y+3z-3=0.$
2.184.
а) Написать уравнение плоскости, проходящей через три заданные точки $M_1(1, 2,0),$ $M_2(2, 1, 1)$ и $M_3(3, 0, 1).$
Решение.
Воспользуемся формулой (4):
$\Rightarrow -x+1+-2z+2y-4+2z+2x-2-y+2=0\Rightarrow x+y-3=0.$
Даны координаты вершины треугольника АВС: А (6; -2); В (1;2); С(3;5).Найдите: 1. Уравнение прямой BN, параллельной стороне АС;
Уравнение прямой, проходящей через точки А и С:
Так как А (6; -2) и С(3;5), получим
Параллельные прямые имеют одинаковые угловые коэффициенты
Уравнение прямой, параллельной АС имеет вид
Для нахождения коэффициента b подставим координаты точки В (1;2)
Уравнение прямой bn параллельной ac
Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут
Неправильный логин или пароль.
Укажите электронный адрес и пароль.
Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.
Инструкция по изменению пароля отправлена на почту.
Чтобы зарегистрироваться, укажите ваш email и пароль
Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.
http://reshaika.com/matematika/1052206.html
http://reshka.feniks.help/vysshaya-matematika/analiticheskaja-geometrija/dany-vershiny-treugolnika-abc