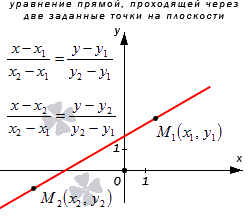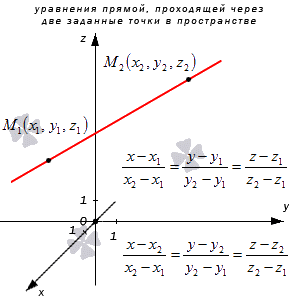Уравнение прямой через две точки как решать

Уравнение прямой, которая проходит через две заданные точки: примеры, решения

Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.

Уравнение прямой, проходящей через две заданные точки на плоскости

Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.

Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.

Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a , проходящей через две несовпадающие точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , находящиеся в декартовой системе координат.

В каноническом уравнении прямой на плоскости, имеющего вид x — x 1 a x = y — y 1 a y , задается прямоугольная система координат О х у с прямой, которая пересекается с ней в точке с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) .

Необходимо составить каноническое уравнение прямой a , которая пройдет через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) .

Прямая а имеет направляющий вектор M 1 M 2 → с координатами ( x 2 — x 1 , y 2 — y 1 ) , так как пересекает точки М 1 и М 2 . Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 ) и координатами лежащих на них точках M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 .

Рассмотрим рисунок, приведенный ниже.

Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ .

Рассмотрим подробней на решении нескольких примеров.

Записать уравнение прямой, проходящей через 2 заданные точки с координатами M 1 — 5 , 2 3 , M 2 1 , — 1 6 .

Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x 1 , y 1 и x 2 , y 2 принимает вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . По условию задачи имеем, что x 1 = — 5 , y 1 = 2 3 , x 2 = 1 , y 2 = — 1 6 . Необходимо подставить числовые значения в уравнение x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . Отсюда получим, что каноническое уравнение примет вид x — ( — 5 ) 1 — ( — 5 ) = y — 2 3 — 1 6 — 2 3 ⇔ x + 5 6 = y — 2 3 — 5 6 .

Ответ: x + 5 6 = y — 2 3 — 5 6 .

При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.

Составить общее уравнение прямой, проходящей через точки с координатами M 1 ( 1 , 1 ) и M 2 ( 4 , 2 ) в системе координат О х у .

Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида x — 1 4 — 1 = y — 1 2 — 1 ⇔ x — 1 3 = y — 1 1 .

Приведем каноническое уравнение к искомому виду, тогда получим:

x — 1 3 = y — 1 1 ⇔ 1 · x — 1 = 3 · y — 1 ⇔ x — 3 y + 2 = 0

Ответ: x — 3 y + 2 = 0 .

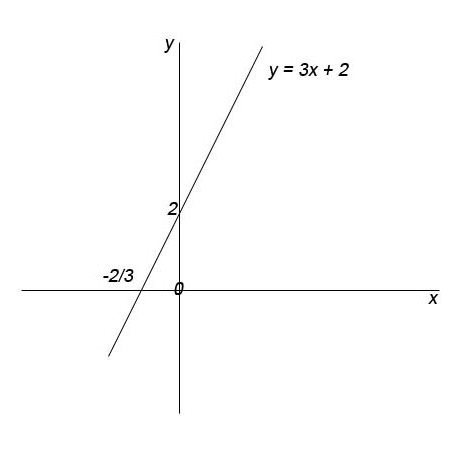
Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y = k x + b . Если необходимо найти значение углового коэффициента k и числа b , при которых уравнение y = k x + b определяет линию в системе О х у , которая проходит через точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , где x 1 ≠ x 2 . Когда x 1 = x 2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М 1 М 2 определена общим неполным уравнением вида x — x 1 = 0 .

Потому как точки М 1 и М 2 находятся на прямой, тогда их координаты удовлетворяют уравнению y 1 = k x 1 + b и y 2 = k x 2 + b . Следует решить систему уравнений y 1 = k x 1 + b y 2 = k x 2 + b относительно k и b .

Для этого найдем k = y 2 — y 1 x 2 — x 1 b = y 1 — y 2 — y 1 x 2 — x 1 · x 1 или k = y 2 — y 1 x 2 — x 1 b = y 2 — y 2 — y 1 x 2 — x 1 · x 2 .

С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 1 или y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 2 .

Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.

Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M 2 ( 2 , 1 ) и y = k x + b .

Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y = k x + b . Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M 1 ( — 7 , — 5 ) и M 2 ( 2 , 1 ) .

Точки М 1 и М 2 располагаются на прямой, тогда их координаты должны обращать уравнение y = k x + b верное равенство. Отсюда получаем, что — 5 = k · ( — 7 ) + b и 1 = k · 2 + b . Объединим уравнение в систему — 5 = k · — 7 + b 1 = k · 2 + b и решим.

При подстановке получаем, что

— 5 = k · — 7 + b 1 = k · 2 + b ⇔ b = — 5 + 7 k 2 k + b = 1 ⇔ b = — 5 + 7 k 2 k — 5 + 7 k = 1 ⇔ ⇔ b = — 5 + 7 k k = 2 3 ⇔ b = — 5 + 7 · 2 3 k = 2 3 ⇔ b = — 1 3 k = 2 3

Теперь значения k = 2 3 и b = — 1 3 подвергаются подстановке в уравнение y = k x + b . Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y = 2 3 x — 1 3 .

Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.

Запишем каноническое уравнение прямой, проходящей через M 2 ( 2 , 1 ) и M 1 ( — 7 , — 5 ) , имеющее вид x — ( — 7 ) 2 — ( — 7 ) = y — ( — 5 ) 1 — ( — 5 ) ⇔ x + 7 9 = y + 5 6 .

Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x + 7 9 = y + 5 6 ⇔ 6 · ( x + 7 ) = 9 · ( y + 5 ) ⇔ y = 2 3 x — 1 3 .

Ответ: y = 2 3 x — 1 3 .

Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве

Если в трехмерном пространстве имеется прямоугольная система координат О х у z с двумя заданными несовпадающими точками с координатами M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , проходящая через них прямая M 1 M 2 , необходимо получить уравнение этой прямой.

Имеем, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z и параметрические вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ способны задать линию в системе координат О х у z , проходящую через точки, имеющие координаты ( x 1 , y 1 , z 1 ) с направляющим вектором a → = ( a x , a y , a z ) .

Прямая M 1 M 2 имеет направляющий вектор вида M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) , где прямая проходит через точку M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , отсюда каноническое уравнение может быть вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , в свою очередь параметрические x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ z = z 1 + ( z 2 — z 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ z = z 2 + ( z 2 — z 1 ) · λ .

Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.

Написать уравнение прямой, определенной в прямоугольной системе координат О х у z трехмерного пространства, проходящей через заданные две точки с координатами M 1 ( 2 , — 3 , 0 ) и M 2 ( 1 , — 3 , — 5 ) .

Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 .

По условию имеем, что x 1 = 2 , y 1 = — 3 , z 1 = 0 , x 2 = 1 , y 2 = — 3 , z 2 = — 5 . Отсюда следует, что необходимые уравнения запишутся таким образом:

x — 2 1 — 2 = y — ( — 3 ) — 3 — ( — 3 ) = z — 0 — 5 — 0 ⇔ x — 2 — 1 = y + 3 0 = z — 5

Ответ: x — 2 — 1 = y + 3 0 = z — 5 .

Уравнение прямой проходящей через две точки

Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.

Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнения прямой, проходящей через две точки могут быть следующих видов:

• каноническое уравнение,
• параметрическое уравнение,
• общее уравнение прямой,
• уравнение прямой с угловым коэффициентом,
• уравнение прямой в полярных координатах и другие.

Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.

Как решить уравнение прямой через две точки?

Математика — не скучная наука, как кажется порой. В ней есть много интересного, хотя порой и непонятного для тех, кто не горит желанием в ней разбираться. Сегодня речь пойдёт об одной из самых часто встречающихся и простых тем в математике, а точнее той её области, что на грани алгебры и геометрии. Поговорим о прямых и их уравнениях. Казалось бы, это скучная школьная тема, которая не сулит ничего интересного и нового. Однако это не так, и в этой статье мы попытаемся вам доказать нашу точку зрения. Прежде чем перейти к самому интересному и описать уравнение прямой через две точки, мы обратимся к истории всех этих измерений, а затем выясним, зачем это всё было нужно и почему сейчас тоже не помешает знание последующих формул.

История

Ещё в древности математики увлекались геометрическими построениями и всевозможными графиками. Трудно сегодня сказать, кто первым придумал уравнение прямой через две точки. Но можно предположить, что этим человеком был Евклид — древнегреческий учёный и философ. Именно он в своём трактате «Начала» зародил основу будущей евклидовой геометрии. Сейчас этот раздел математики считается основой геометрического представления мира и проходится в школе. Но стоит сказать, что евклидова геометрия действует только на макроуровне в нашем трёхмерном измерении. Если же рассматривать космос, то не всегда удаётся представить с помощью неё все те явления, что там происходят.

После Евклида были и другие учёные. И они совершенствовали и осмысляли то, что он открыл и написал. В конце концов, получилась устойчивая область геометрии, в которой всё до сих пор остаётся незыблемым. И уже тысячелетиями доказано, что уравнение прямой через две точки составить очень легко и просто. Но прежде чем приступить к объяснению того, как это сделать, обсудим немного теории.

Теория

Прямая — это бесконечный в обоих направлениях отрезок, который можно поделить на бесконечное множество отрезков любой длины. Для того чтобы представить прямую, чаще всего используют графики. Причём графики могут быть как в двумерной, так и в трёхмерной системе координат. И строятся они по координатам точек, им принадлежащих. Ведь если рассматривать прямую, то можно заметить, что она состоит из бесконечного множества точек.

Однако есть то, чем прямая очень сильно отличается от других видов линий. Это её уравнение. В общем виде оно очень простое, в отличие, скажем, от уравнения окружности. Наверняка, каждый из нас проходил его ещё в школе. Но всё же запишем его общий вид: y=kx+b. В следующем разделе мы подробно разберём, что означает каждая из этих букв и как решать это незамысловатое уравнение прямой, проходящей через две точки.

Уравнение прямой

То равенство, что было представлено выше, и является необходимым нам уравнением прямой. Стоит пояснить, что здесь что означает. Как можно догадаться, y и x — это координаты каждой точки, принадлежащей прямой. Вообще, уравнение это существует только потому, что каждой точке любой прямой свойственно находиться в связи с другими точками, а поэтому существует закон, связывающий одну координату с другой. Этот закон и определяет, как выглядит уравнение прямой через две данные точки.

Почему именно две точки? Всё это потому, что минимально количество точек, необходимое для построения прямой в двумерном пространстве, равно двум. Если же брать трёхмерное пространство, то количество точек, необходимое для построения одной-единственной прямой также будет равно двум, так как три точки уже составляют плоскость.

Существует также теорема, доказывающая, что через две любые точки возможно провести единственную прямую. Этот факт можно проверить на практике, соединив линейкой две случайные точки на графике.

Теперь рассмотрим конкретный пример и покажем, как решать это пресловутое уравнение прямой, проходящей через две данные точки.

Пример

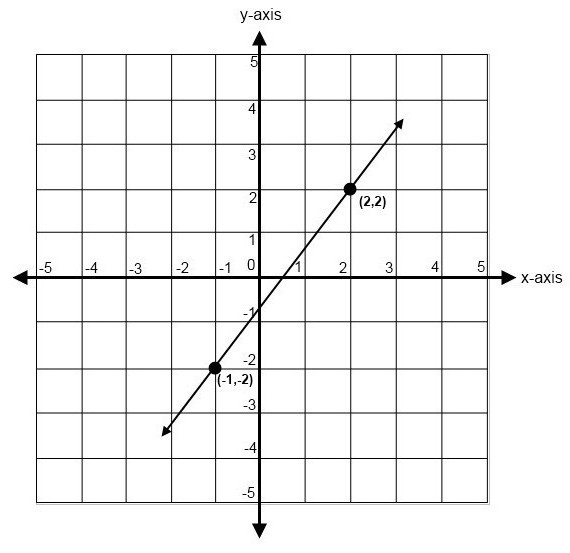
Рассмотрим две точки, через которые нужно построить прямую. Зададим им координаты, например, М₁(2;1) и М₂(3;2). Как мы знаем из школьного курса, первая координата — это значение по оси OX, а вторая — по оси OY. Выше было приведено уравнение прямой через две точки, и, чтобы нам узнать недостающие параметры k и b, нужно составить систему из двух уравнений. Фактически она будет составлена из двух уравнений, в каждом из которых будут две наши неизвестные постоянные:

Теперь остаётся самое главное: решить эту систему. Делается это довольно просто. Для начала выразим из первого уравнения b: b=1-2k. Теперь надо подставить полученное равенство во второе уравнение. Делается это заменой b на полученное нами равенство:

Теперь, когда мы узнали, чему равно значение коэффициента k, пора узнать величину следующей постоянной — b. Делается это ещё проще. Так как нам известна зависимость b от k, мы можем подставить значение последней в первое уравнение и узнать неизвестное значение:

Зная оба коэффициента, теперь можем подставить их в исходное общее уравнение прямой через две точки. Таким образом, для нашего примера получаем такое уравнение: y=x-1. Это и есть искомое равенство, которое мы должны были получить.

Перед тем как перейти к заключению, обсудим применение этого раздела математики в повседневной жизни.

Применение

Как такового применения уравнение прямой через две точки не находит. Но это не значит, что это не нужно нам. В физике и математике очень активно применяются уравнения прямых и свойства, из них вытекающие. Вы можете это даже не замечать, но математика окружает нас. И даже такие, на первый взгляд, ничем не примечательные темы, как уравнение прямой через две точки, оказываются очень полезны и очень часто применяются на фундаментальном уровне. Если на первый взгляд кажется, что это совсем нигде не может пригодиться, то вы ошибаетесь. Математика развивает логическое мышление, которое никогда не будет лишним.

Заключение

Теперь, когда мы разобрались с тем, как строить прямые по двум данным точкам, нам ничего не стоит ответить на любой вопрос, связанный с этим. Например, если преподаватель скажет вам: » Напишите уравнение прямой, проходящей через две точки», то вам не составит труда сделать это. Надеемся, что эта статья была полезной для вас.