Уравнение прямой дм перпендикулярной плоскости авс

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости

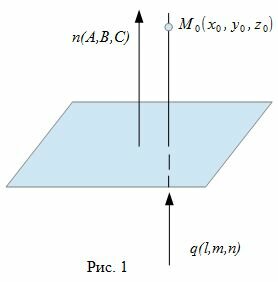
Наша цель построить уравнение прямой, проходящей через данную точку M₀ и перпендикулярной к данной плоскости Ax+By+Cz+D=0.

Общее уравнение плоскости имеет вид:

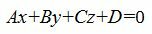(1)

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

(2)

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональный плоскости (1) имеет следующий вид:

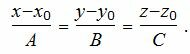(3)

Пример 1. Построить прямую, проходящую через точку M₀(5, -4, 4) и перпендикулярной плоскости

Общее уравнение плоскости имеет вид (1), где :

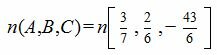(4)

Подставляя координаты точки M₀(5, -4, 4) и координаты нормального вектора плоскости (4) в (3), получим:

Уравнения прямой, которая проходит через заданную точку и перпендикулярна к заданной плоскости.

В этой статье мы разберемся с нахождением уравнений прямой, которая в прямоугольной системе координат в трехмерном пространстве проходит через заданную точку и перпендикулярна к заданной плоскости. Сначала разберем принцип составления уравнений такой прямой, после чего перейдем к решению задач.

Навигация по странице.

Принцип составления уравнений прямой, проходящей через заданную точку перпендикулярно к заданной плоскости.

Прежде чем приступить к составлению уравнений прямой, которая проходит через заданную точку пространства перпендикулярно к заданной плоскости, освежим в памяти один момент.

В 10 классе на уроках геометрии доказывается теорема: через любую точку трехмерного пространства проходит единственная прямая, перпендикулярная к заданной плоскости. Таким образом, мы можем определить конкретную прямую, указав точку, через которую она проходит, и плоскость, к которой она перпендикулярна.

Сформулируем условие задачи.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , задана точка , плоскость и требуется написать уравнения прямой a , проходящей через точку М₁ перпендикулярно к заданной плоскости .

Решим эту задачу.

Нам известны координаты точки M₁ , через которую проходит прямая a , уравнения которой нам требуется найти. Но этого мало, чтобы записать уравнения прямой a . Если мы будем знать еще координаты направляющего вектора прямой a , то сможем записать канонические уравнения прямой a в пространстве и параметрические уравнения прямой a в пространстве.

Как же определить координаты направляющего вектора прямой a ? Да очень просто. Так как по условию прямая a перпендикулярна к плоскости , то нормальный вектор плоскости является направляющим вектором прямой a . Таким образом, нам остается отыскать координаты нормального вектора плоскости , принять их за соответствующие координаты направляющего вектора прямой a и записать требуемые уравнения прямой a .

В свою очередь координаты нормального вектора плоскости находятся в зависимости от способа задания плоскости в прямоугольной системе координат Oxyz . Если плоскости в прямоугольной системе координат Oxyz отвечает общее уравнение плоскости вида , то нормальным вектором плоскости является вектор . Если плоскость задается уравнением плоскости в отрезках , то от него следует перейти к общему уравнению плоскости , откуда станут видны координаты нормального вектора плоскости : . Если плоскость задана каким-либо другим способом (например, с помощью трех точек, не лежащих на одной прямой, или с помощью уравнений двух пересекающихся прямых, или с помощью уравнений двух параллельных прямых), то на основании этих данных следует определить общее уравнение плоскости , откуда получить координаты ее нормального вектора.

Итак, задача нахождения уравнений прямой, которая проходит через заданную точку пространства и перпендикулярна к заданной плоскости, решена. Осталось лишь рассмотреть несколько решенных примеров.

Примеры нахождения уравнений прямой, которая проходит через заданную точку пространства и перпендикулярна к заданной плоскости.

В этом пункте статьи мы приведем подробные решения наиболее характерных задач, в которых находятся уравнения прямой, проходящей через заданную точку пространства перпендикулярно к заданной плоскости.

Начнем с самого простого случая, когда требуется написать уравнения прямой, проходящей через заданную точку перпендикулярно к одной из координатных плоскостей.

Напишите канонические уравнения прямой a , которая проходит через точку и перпендикулярна координатной плоскости Oyz .

Нормальным вектором координатной плоскости Oyz является координатный вектор . Так как прямая a перпендикулярна плоскости Oyz , то является ее направляющим вектором. Итак, мы знаем координаты точки, лежащей на прямой a , и координаты ее направляющего вектора, то есть, можем написать ее канонические уравнения: .

.

Аналогично решается задача, в условии которой даны координаты точки, через которую проходит прямая, и задана плоскость с помощью общего уравнения плоскости.

Составьте параметрические уравнения прямой a , проходящей через точку перпендикулярно к плоскости .

Направляющим вектором прямой a является нормальный вектор плоскости , то есть, . Теперь мы можем записать требуемые уравнения прямой a . Они имеют вид .

.

В заключении рассмотрим пример составления уравнений прямой, которая проходит через заданную точку пространства и перпендикулярна к плоскости, заданной тремя не лежащими на одной прямой точками.

В прямоугольной системе координат Oxyz в трехмерном пространстве заданы три точки . Напишите уравнения прямой a , проходящей через начало координат перпендикулярно к плоскости ABC .

Направляющим вектором прямой, проходящей через начало координат перпендикулярно к плоскости АВС , является нормальный вектор плоскости АВС . Нормальным вектором плоскости АВС является векторное произведение векторов и . Найти указанное векторное произведение мы сможем, если будем знать координаты векторов и . Вычислим координаты векторов и по координатам точек А , В и С (при необходимости смотрите статью нахождение координат вектора по координатам точек его конца и начала): .

Тогда, , а в координатной форме (при необходимости обращайтесь к статье координаты вектора).

Теперь мы можем записать требуемые уравнения прямой a , которая проходит через точку и перпендикулярна к плоскости ABC : .

Приведем второй способ решения этой задачи.

Составим уравнение плоскости, проходящей через три заданные точки А , В и С , , откуда виден нормальный вектор этой плоскости . Далее принимаем этот вектор за направляющий вектор прямой a и записываем ее уравнения.

.

Урок геометрии по теме «Перпендикулярность прямой и плоскости». 10-й класс

Разделы: Математика

Класс: 10

Цели:

1. закрепить вопросы теории по теме «Перпендикулярность прямой и плоскости»;
2. вырабатывать навыки применения теоретических знаний к решению типовых задач на перпендикулярность прямой и плоскости.

План:

1. Теоретический опрос.
   1. Доказательство изученных теорем у доски.
   2. Фронтальный опрос.
   3. Презентации учащихся по данной теме.
2. Решение задач.
   1. Решение устных задач по готовым чертежам.
   2. Решение письменных задач (по группам).
   3. Самостоятельная работа с индивидуальным заданием.
3. Итог урока. Задание на дом.

Ход урока

I. Теоретический опрос (4 ученика у доски)

1) доказать лемму о 2-ух параллельных прямых, одна из которых перпендикулярна к третьей;
2) доказать теорему о 2-ух параллельных прямых, одна из которых перпендикулярна к плоскости;
3) доказать обратную теорему о параллельности 2-ух прямых, перпендикулярных к плоскости;
4) доказать признак перпендикулярности прямой и плоскости.

Пока ученики готовятся у доски к ответу, с классом проводится фронтальный опрос.
(С помощью мультимедиапроектора на экране появляются вопросы (Приложение 1), и ученики отвечают на них)

1. Закончить предложение:

а) две прямые в пространстве называются перпендикулярными, если… (угол между ними равен 90°)
б) прямая называется перпендикулярной к плоскости, если… (она перпендикулярна к любой прямой, лежащей в этой плоскости)
в) если две прямые перпендикулярны к плоскости, то они… (параллельны)
г) если плоскость перпендикулярна к одной из двух параллельных прямых, то она… (перпендикулярна и к другой прямой)
д) если две плоскости перпендикулярны к одной прямой, то они… (параллельны)

2. Дан параллелепипед

б) Определите взаимное расположение:
1) прямой CC₁ и плоскости (DСВ) (ответ: они перпендикулярны)
2) прямой D₁C₁ и плоскости (DCB) (ответ: они параллельны)

Далее выслушиваются ответы учеников у доски с дополнениями и исправлениями по необходимости. Затем рассматриваются презентации по данной теме, подготовленные рядом учеников в качестве зачётных работ (Приложение 2, Приложение 3, Приложение 4).
(Накануне изучения каждой темы учащимся предлагается такой вариант зачёта)

II. Решение задач.

1. Решение задач по готовым чертежам (Устно)

№1

Дано: ∆ ABC — прямоугольный; AM ⊥ AC; M ∉ (ABC)
Доказать: AC ⊥ (AMB)
Доказательство: Т.к. AC ⊥ AB и AC ⊥ AM, а AM ⋂ AB, т.е. АМ и АВ лежат в плоскости (АМВ), то AC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.

№2

Дано: ВМDC — прямоугольник, M ∉ (ABC), MB ⊥ AB
Доказать: CD ⊥ (ABC)
Доказательство: MB ⊥ BC, т.к. ВМDC – прямоугольник, MB ⊥ AB по условию, BC ⋂ AB, т.е. ВС и АВ лежат в плоскости (АВС) ⇒ MB ⊥ (ABC) по признаку перпендикулярности прямой и плоскости. СD ∥ МВ по свойству сторон прямоугольника ⇒ CD ⊥ (ABC) по теореме о двух параллельных прямых, одна из которых перпендикулярна к плоскости (то и другая прямая перпендикулярна к этой плоскости).
Ч.т.д.

№3

Дано: АВСD – прямоугольник, M ∉ (ABC), MB ⊥ BC
Доказать: AD ⊥ AM
Доказательство:
1) ∠ABC = 90°, т.к. АВСD – прямоугольник ⇒ BC ⊥ AB, BS ⊥ MB по условию, MB ⋂ AB = B, т.е. МВ и АВ лежат в плоскости (АМВ) ⇒ BC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
2) BC ∥ AD (по свойству сторон прямоугольника) ⇒ AD ⊥ (AMB) по теореме о двух параллельных прямых, одна из которых перпендикулярна плоскости (то и другая прямая перпендикулярна к этой плоскости).
3) Т.к. AD ⊥ (AMB) ⇒ AD ⊥ AM по определению прямой, перпендикулярной плоскости.
Ч.т.д.

№4

Дано: АВСD – параллелограмм, M ∉ (ABC), МВ = МD, МА = МС
Доказать: MO ⊥ (ABC)
Доказательство:
1) Т.к. О – точка пересечения диагоналей параллелограмма, то АО = СО и ВО = DO. ∆ BMD — равнобедренный, т. к. ВМ = МD по условию, значит МО — медиана и высота, т.е. MO ⊥ BD.
2) Аналогично доказывается в ∆ AMC: MO ⊥ AC.
3) Итак, MO ⊥ BD и MO ⊥ AC. а ВD и АС – пересекающиеся прямые, лежащие в плоскости (АВС) ⇒ MO ⊥ (ABC) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.

(Устные ответы к каждой задаче требуется обосновывать, проговаривая всякий раз формулировки применяемых теорем)

2. Решение письменных задач

Класс делится на три группы (например, по рядам), и каждой группе даётся задача с последующей проверкой решения у доски.

№1.2 (№125 учебника)

Через точки P и Q прямой РQ проведены прямые, перпендикулярные к плоскости α и пересекающие её соответственно в точках P₁ и Q₁. Найдите P₁Q₁, если PQ = 15 cм; PP₁ = 21,5 cм; QQ₁ = 33,5 cм.
Решение:

1) PP₁ ⊥ α и QQ₁ ⊥ α по условию ⇒ PP₁ ∥ QQ₁ (обосновать);
2) PP₁ и QQ₁ определяют некоторую плоскость β, α ⋂ β = P₁Q₁;
3) PP₁Q₁Q — трапеция с основаниями PP₁ и QQ₁, проведём PK ∥ P₁Q₁;
4) QK = 33,5 — 21,5 = 12 (см)

P1Q1 = PK =

= 9 см.

№2.2

1) ∆ ABD: ∠BAD = 90°; АD = BC = 8 см;

ВD =

см;

2) ∆ DD₁B: ∠D₁DB = 90°;

DD1 =

= 12 см;

3) SBB1D1D = BD ∙ DD1 =

см 2 .

Ответ:

см 2 .

№3.2

Отрезок МН пересекает плоскость α в точке К. Из концов отрезка проведены прямые МЕ и НР, перпендикулярные к плоскости α. НР = 4 см; МЕ = 12 см; НК = 5 см. Найдите отрезок РЕ.
Решение:

1) Т.к. прямые МЕ и НР перпендикулярны к плоскости α, то МЕ ∥ НР (обосновать) и через них проходит некоторая плоскость β. α ⋂ β = EP;
2)МЕ ⊥ EP; НР ⊥ EP(обосновать), т.е. ∠MEK = ∠HPK = 90°;

3) ∆ HPK: KP =

= 3 см;

4) ∠EMK = ∠PHK (накрест лежащие для параллельных прямых МЕ и НР и секущей МН),

тогда ∆ MEK ∆ HPK по двум углам и

; т.е.

⇒ EK =

= 9 см,

РЕ = РК + КЕ, РЕ = 3 + 9 = 12 см.

Ответ: РЕ = 12 см.

3. Самостоятельная работа (направлена на проверку усвоения материала по данной теме)

1) AA₁ ⊥ AB, AA₁ ⊥ AD, а AB ⋂ AD = A ⇒ AA₁ ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. AA₁ ∥ BB₁, то BB₁ ⊥ (ABC) ⇒ BB₁ ⊥ BD;
2) ∆ ABD: ∠BAD = 90°. По теореме Пифагора:

BD =

= 20 см;

3) ∆ B₁BD – прямоугольный. По теореме Пифагора:

B1B =

= 15 см.

1) BB₁ ⊥ AB, BB₁ ⊥ BC, а AB ⋂ BC = B ⇒ BB₁ ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. BB₁ ∥ AA₁, то AA₁ ⊥ (ABC) ⇒ AA₁ ⊥ AC;
2) Используя свойство диагоналей ромба, имеем в ∆ AOB: ∠AOB = 90°, BO = ½ BD = 8 см. По теореме Пифагора:

AO =

= 6 см,

AO = ½ AC ⇒ AC = 12 см;
3) ∆ A₁AC – прямоугольный. По теореме Пифагора:

AA1 =

= 5 см.

Индивидуальное задание для более сильных учеников. (Вариант III)

1) Т.к. CD ⊥ (FDC) ⇒ CD ⊥ AC и CD ⊥ BC, т.е. ∆ ADC, ∆ BDC – прямоугольные;
2) ∆ ADC = ∆ BDC (по двум катетам) ⇒ AD = BD, т.е. ∆ ADB – равнобедренный и DM – медиана, а значит и высота; 3) DC ⊥ MC ⇒ MCD – прямоугольный,

тогда MC =

= 9;

4) ∆ ABC – равносторонний, поэтому СМ – медиана и высота, т.е. ∆ MCB – прямоугольный, ∠B = 60°,

sin ∠B =

, тогда

,

а АВ = ВС (по условию).
5) S_{∆ ADB} = ½ DM ∙ AB;

S∆ ADB = ½ ∙ 15 ∙

.

Ответ:

III. Подводятся итоги урока. Задание на дом: повторить теоретический материал по изученной теме, глава II, №130, №131.

Для подготовки к уроку использовались материалы учебника «Геометрия – 10-11» авторов Л.С. Атанасяна, В.Ф. Бутузова и др., методические рекомендации к учебнику «Изучение геометрии в 10-11 классах» авторов С.М. Саакяна, В.Ф. Бутузова, «Поурочные разработки по геометрии» автора В.А. Яровенко.