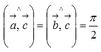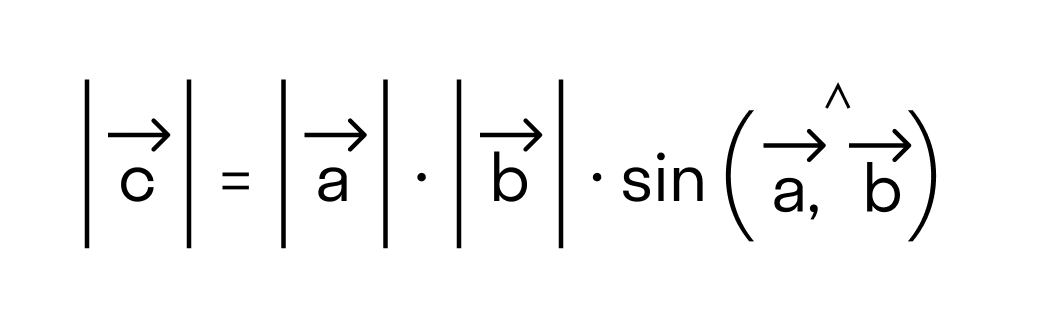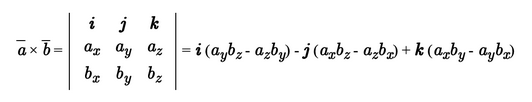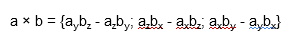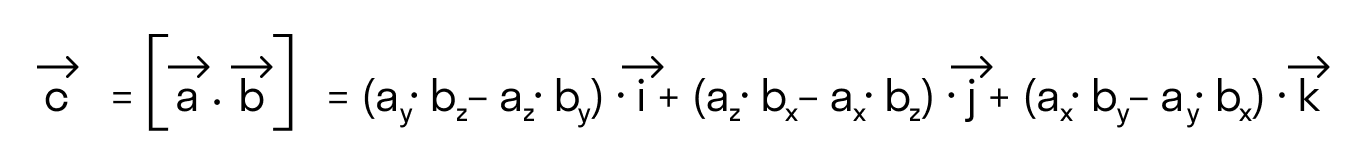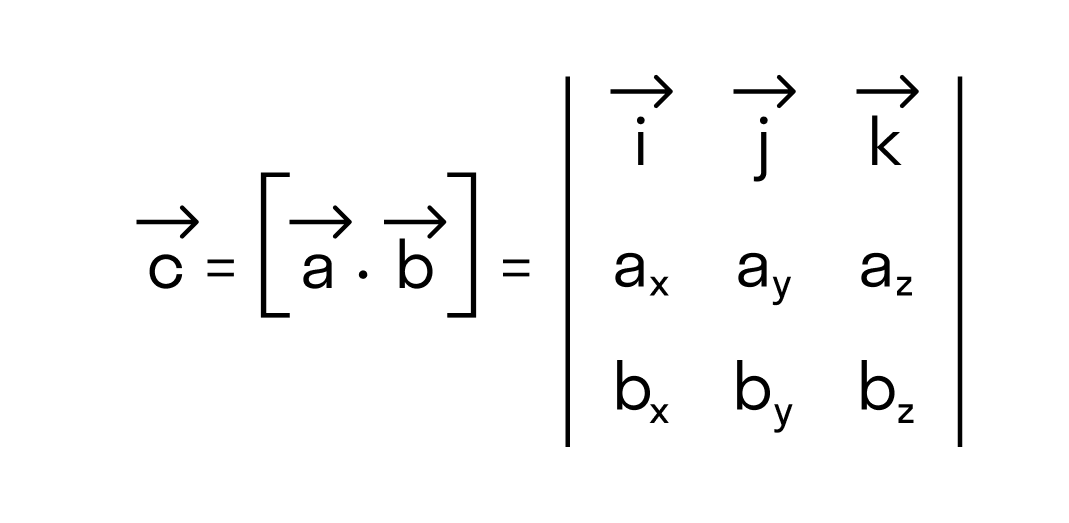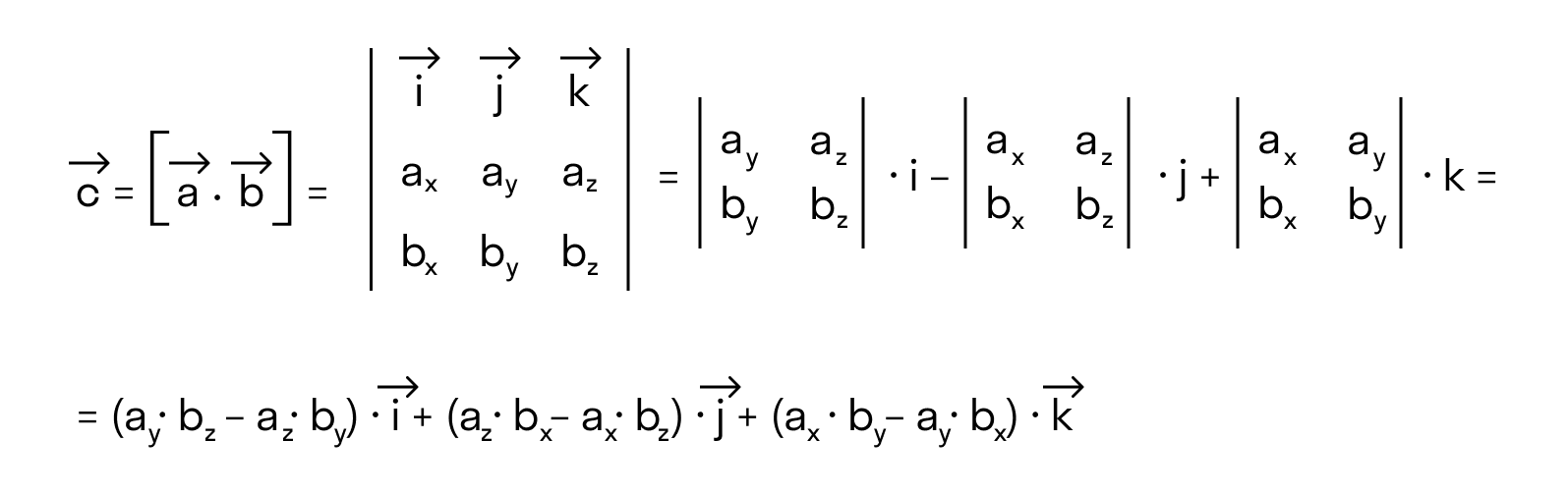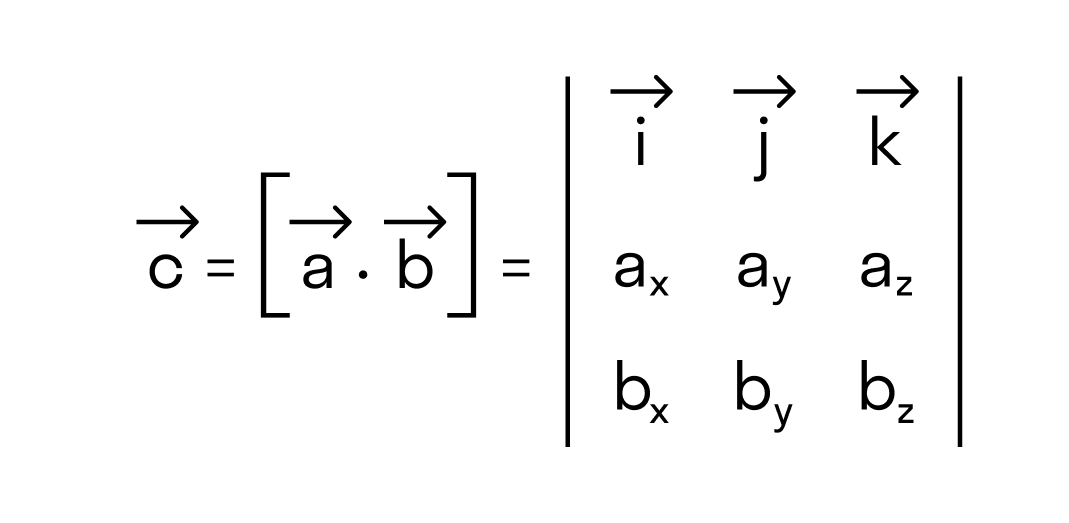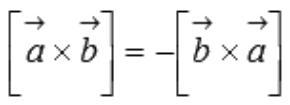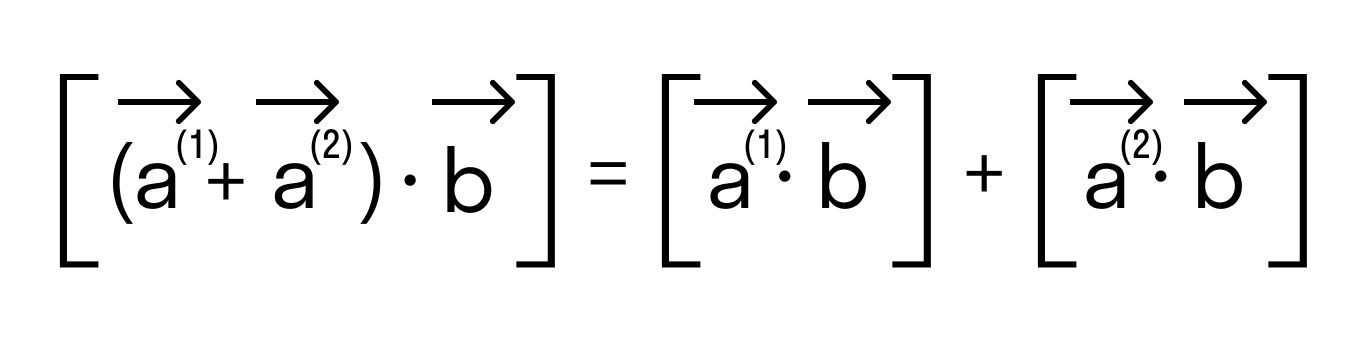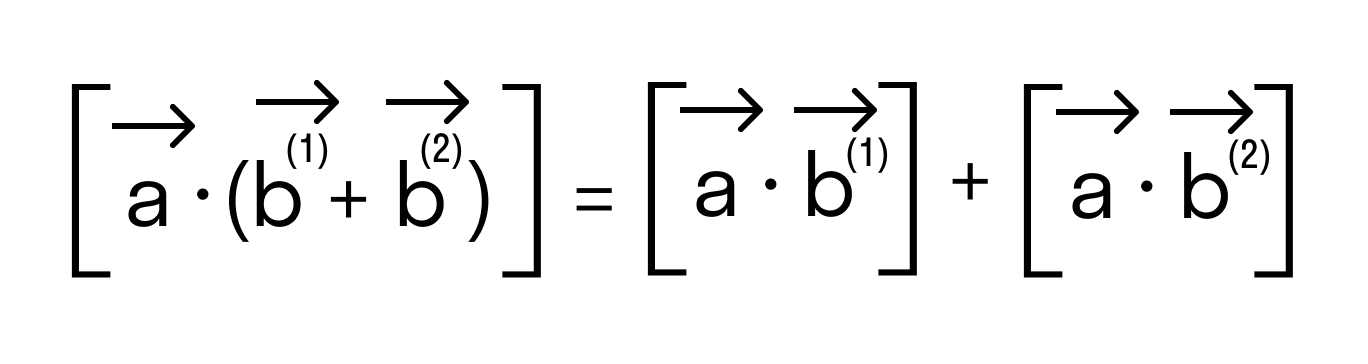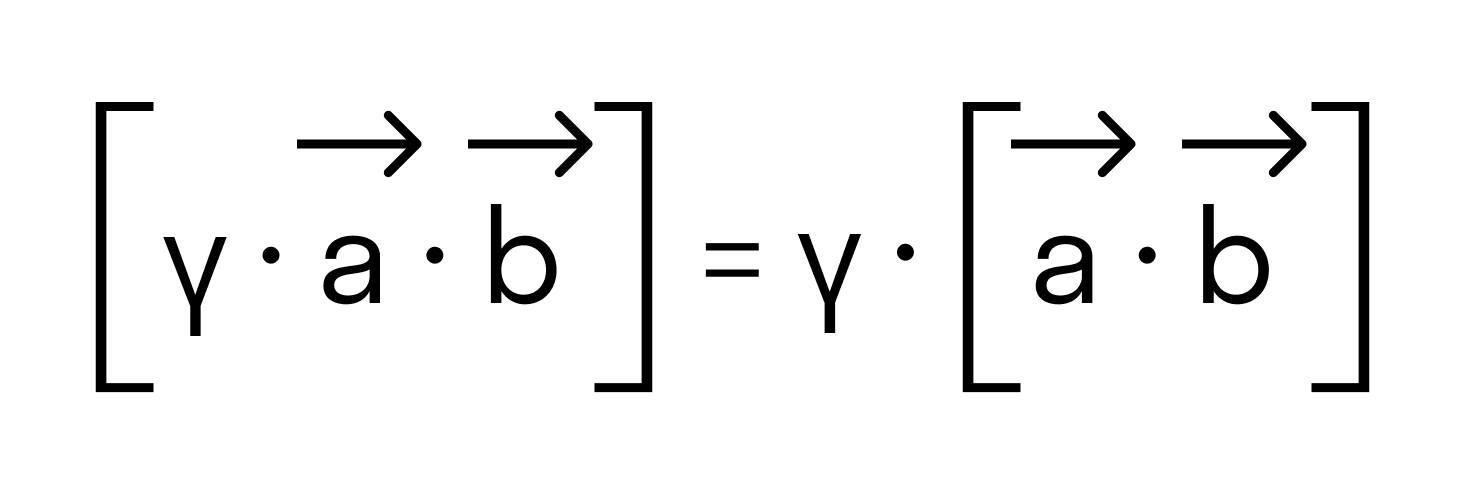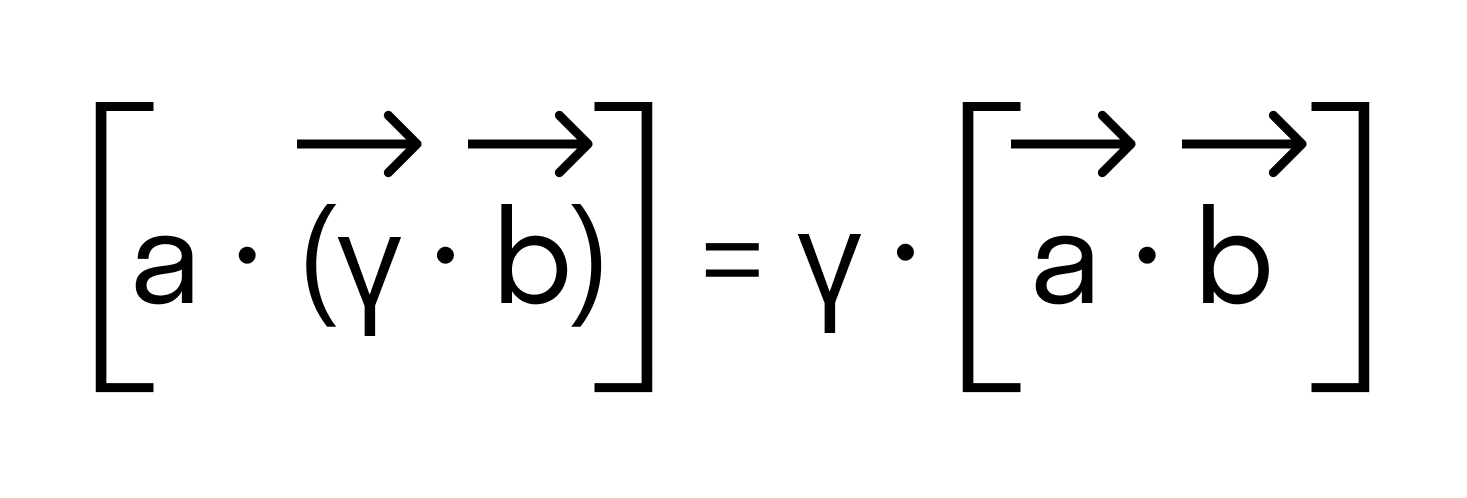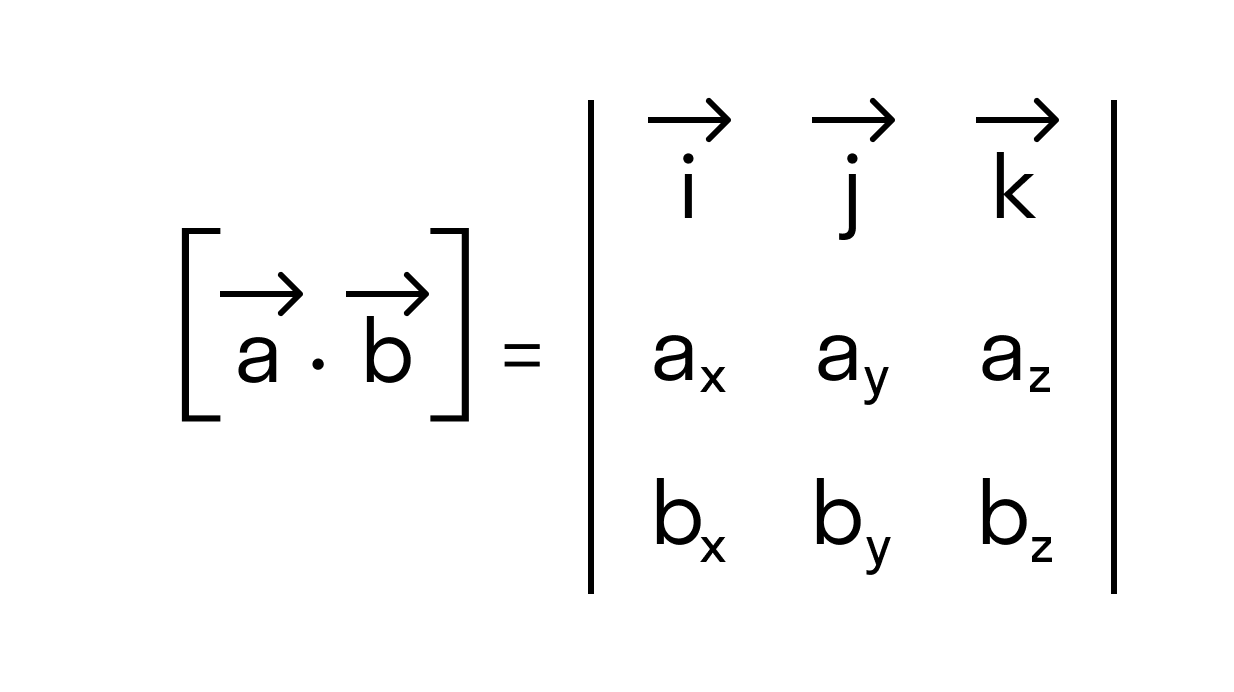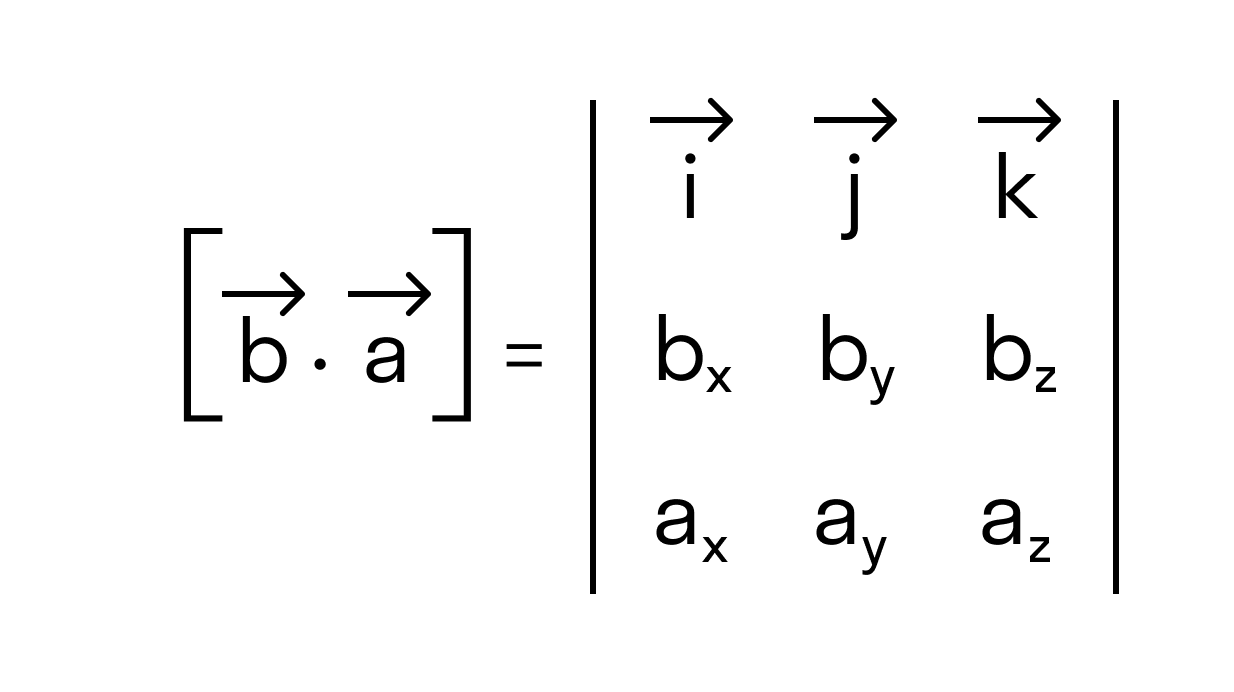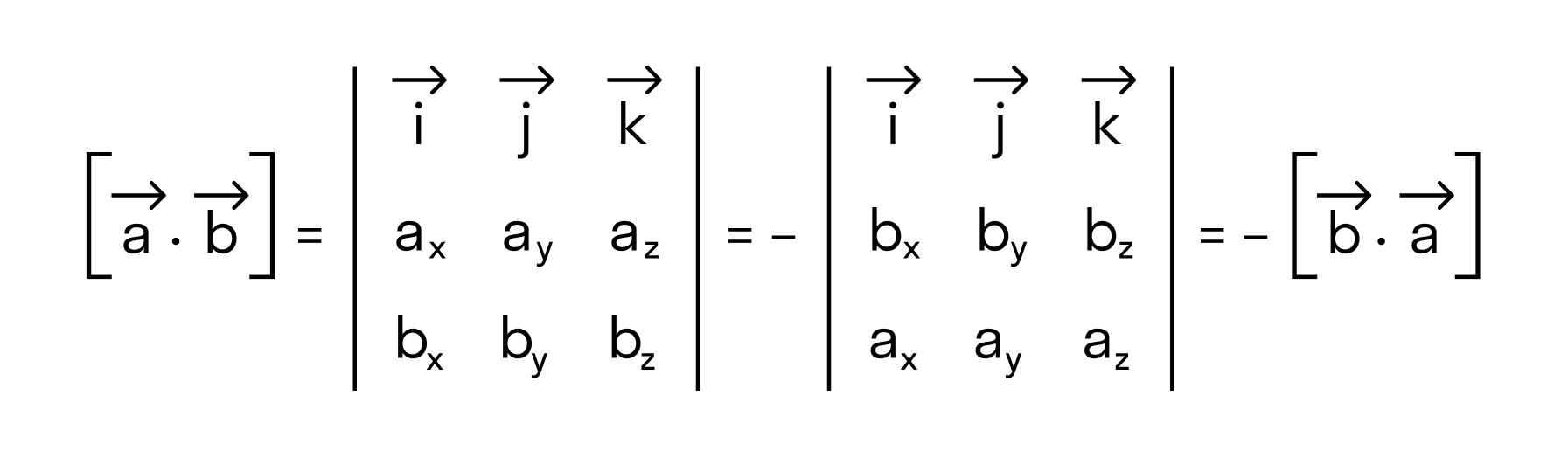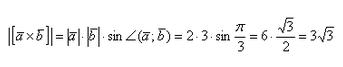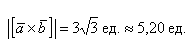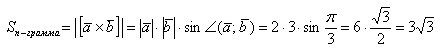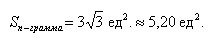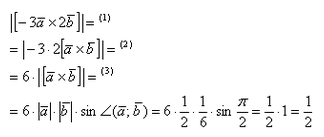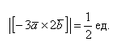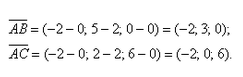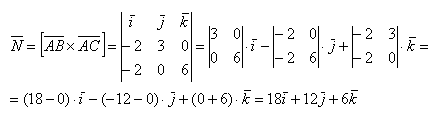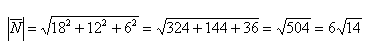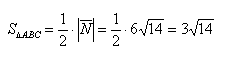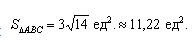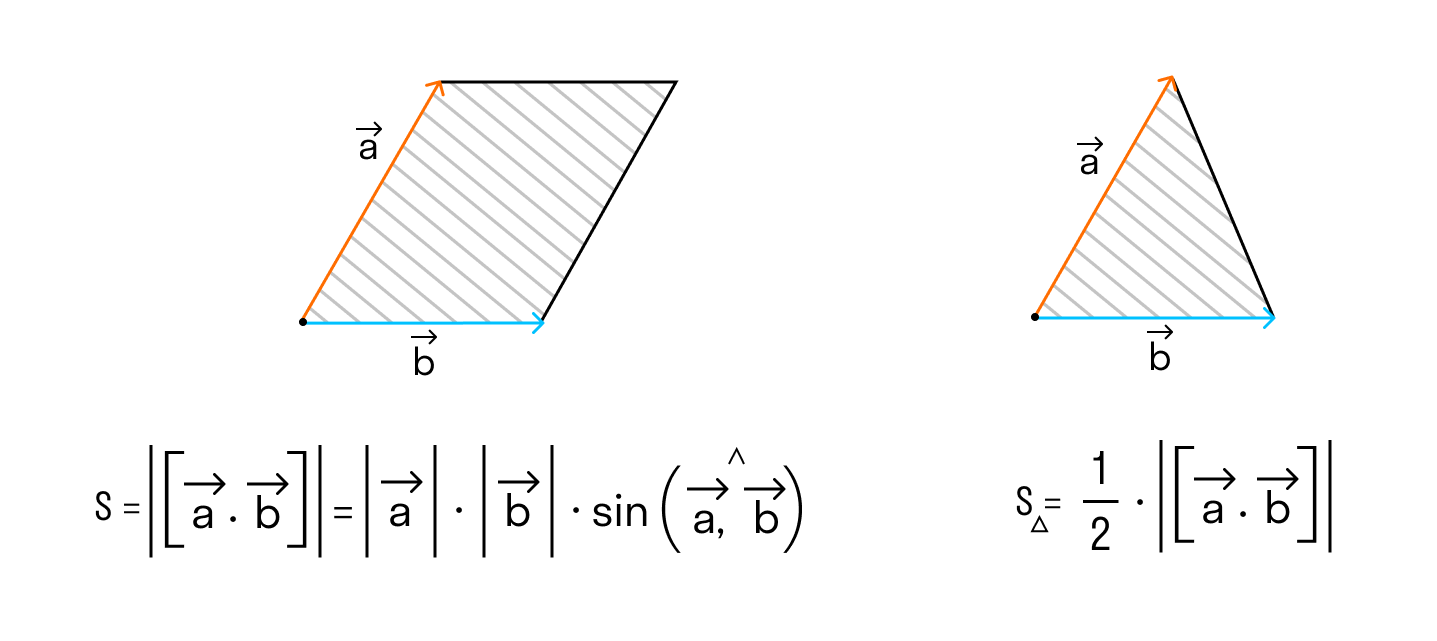Уравнение прямой если векторное произведение

Векторное произведение векторов

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение векторного произведения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

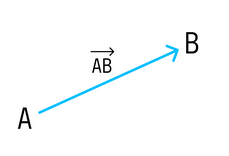
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.

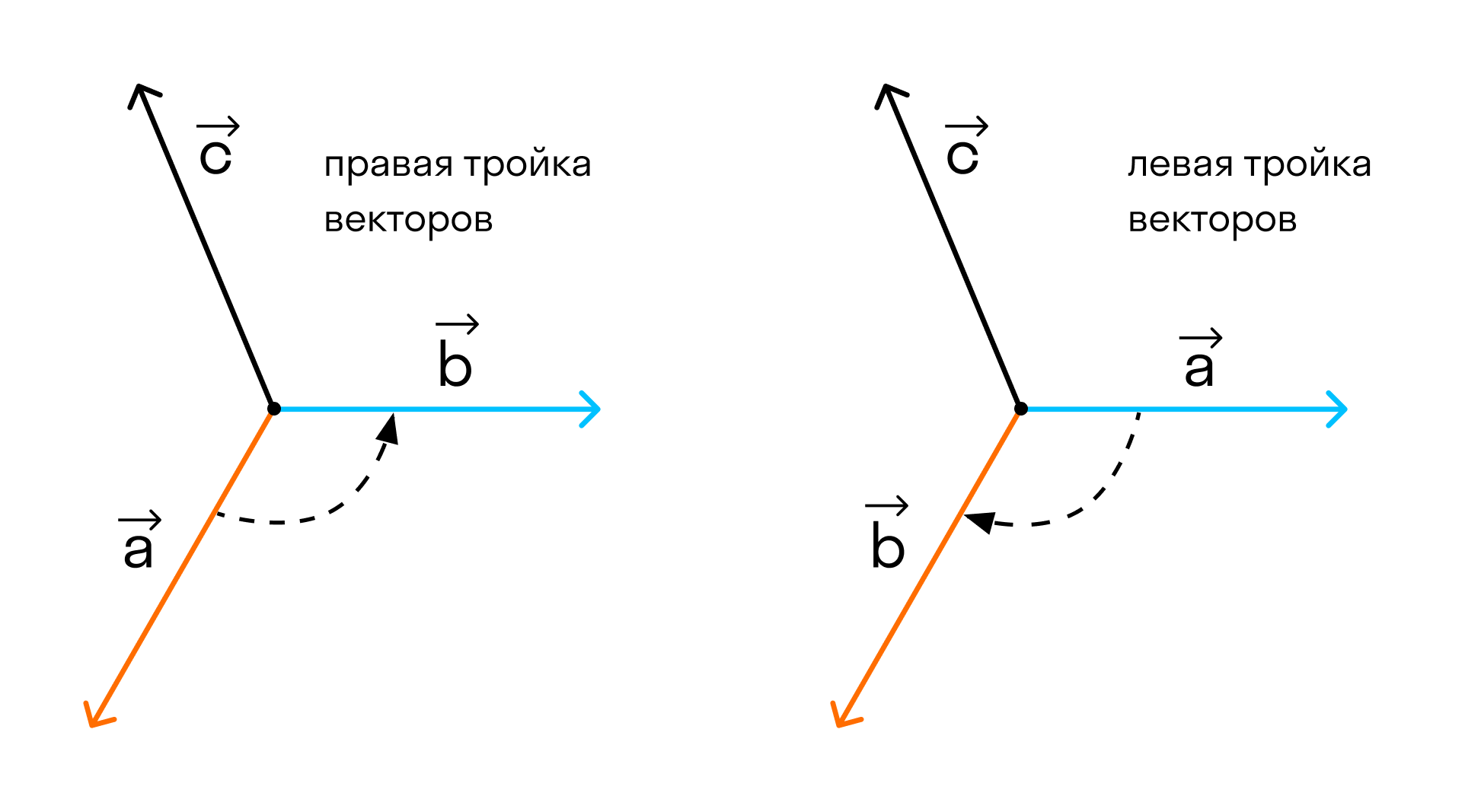
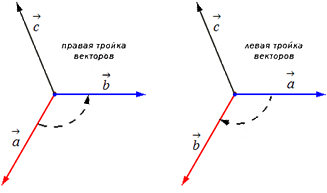
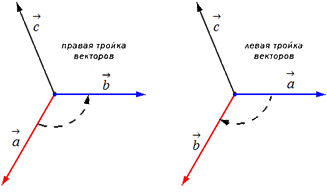
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.

Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.

Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.

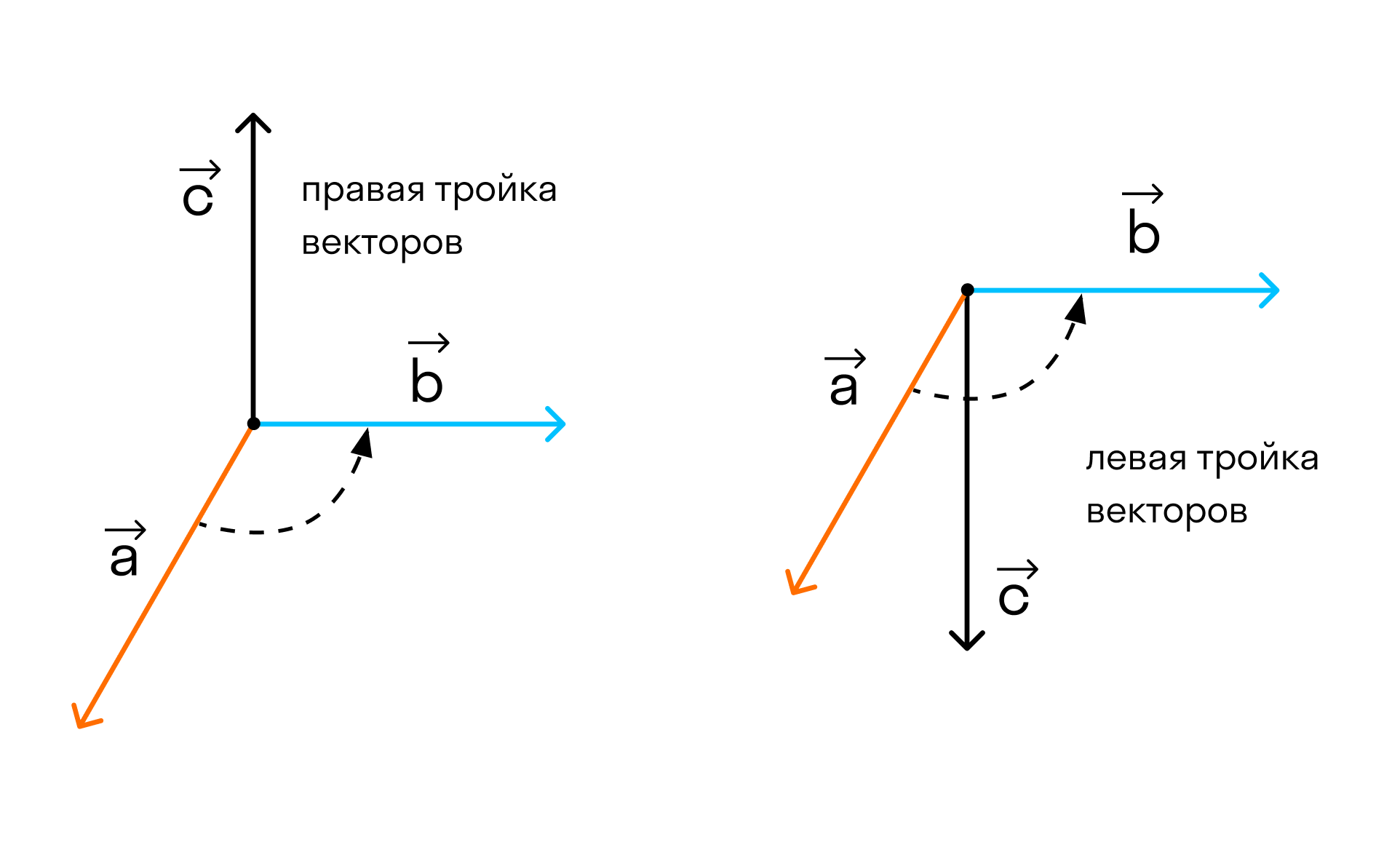
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.

Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.

В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.

И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.

Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!

Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:

• он является нулевым, если векторы →a и →b коллинеарны;
• он перпендикулярен и вектору →a и вектору →b;
  
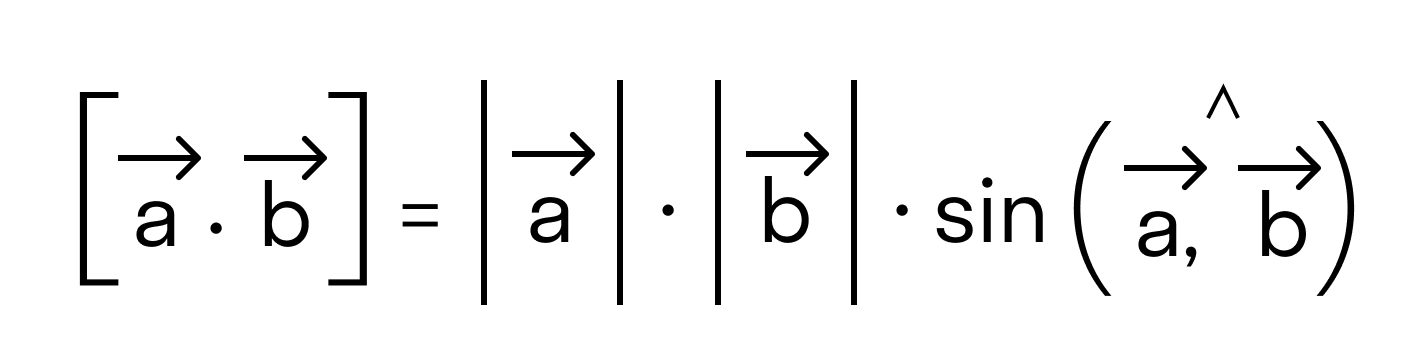
• длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
  
• тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.

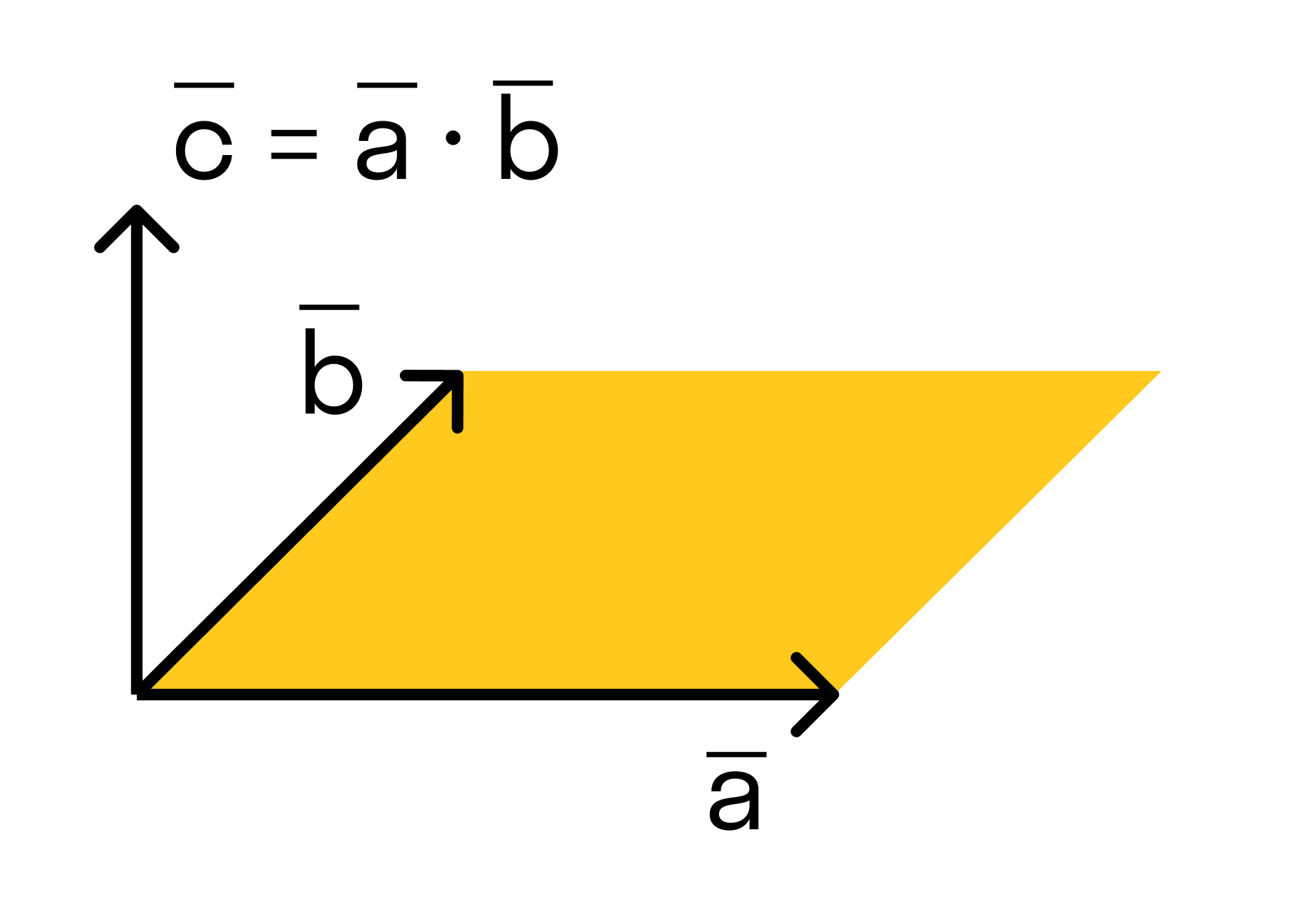
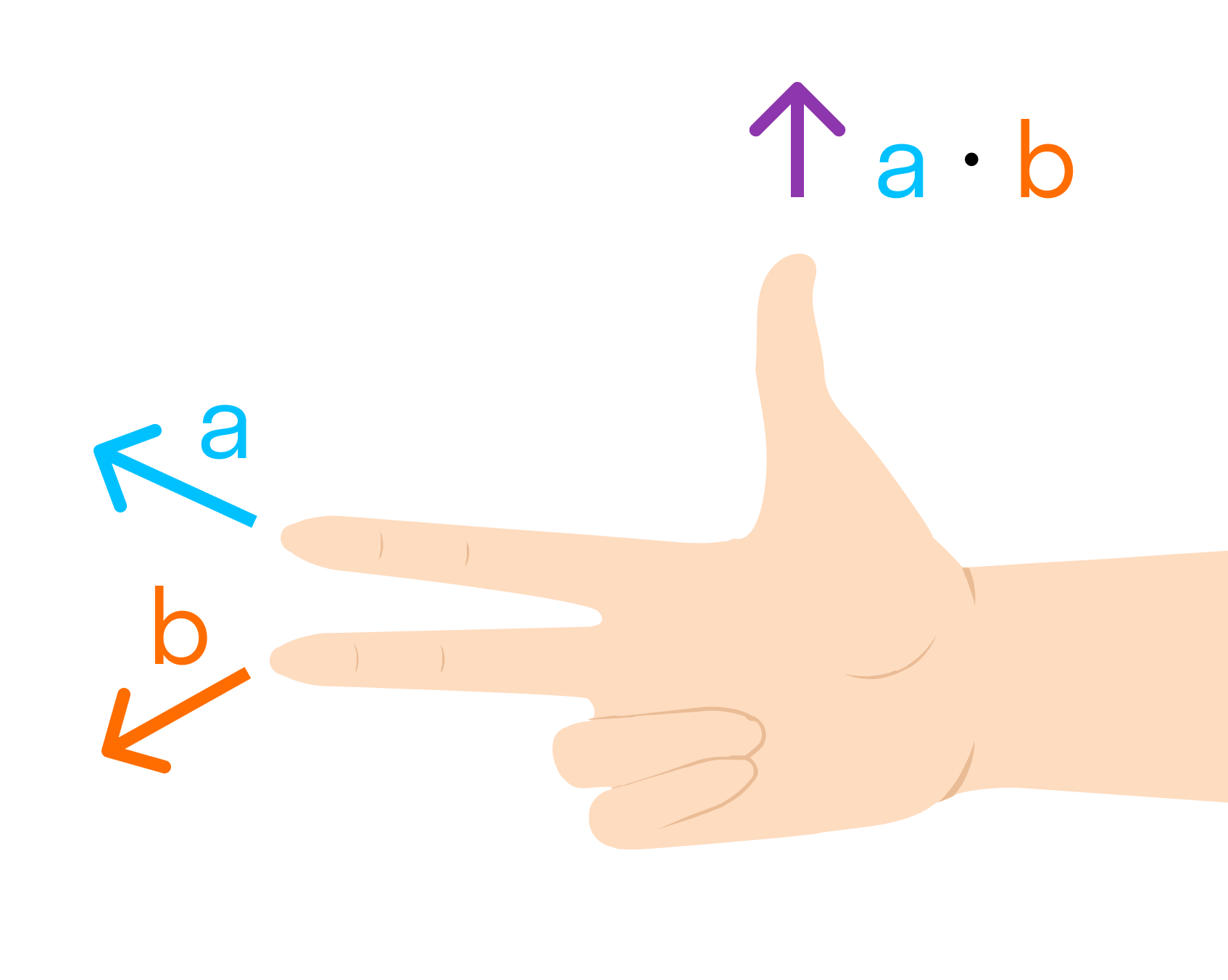
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.

Векторное произведение двух векторов a = и b = в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:

Векторное произведение векторов →a и →b обозначается как [→a • →b].

Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.

Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.

Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:

• Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
• Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
• Если определитель равен нулю, то векторы компланарны (линейно зависимы).

Координаты векторного произведения

Рассмотрим векторное произведение векторов в координатах.

Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.

В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор

→i, →j, →k — координатные векторы.

Это определение показывает нам векторное произведение в координатной форме.

Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:

Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:

Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.

Свойства векторного произведения

Векторное произведение в координатах представляется в виде определителя матрицы:

На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:

1. Антикоммутативность
   
2. Свойство дистрибутивности
   

Сочетательное свойство

, где λ произвольное действительное число.

Для большей ясности докажем свойство антикоммутативности векторного произведения.

Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому

что доказывает свойство антикоммутативности векторного произведения.

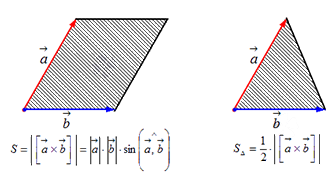
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.

Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).

Примеры решения задач

Пример 1

а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:

Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.

б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:

Пример 2

Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.

По условию снова нужно найти длину векторного произведения. Используем нашу формулу:

Согласно ассоциативным законам, выносим константы за переделы векторного произведения.

Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.

Пример 3

Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.

Сначала найдём векторы:

Затем векторное произведение:

Вычислим его длину:

Подставим данные в формулы площадей параллелограмма и треугольника:

Геометрический смысл векторного произведения

По определению длина векторного произведения векторов равна

А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.

Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.

Физический смысл векторного произведения

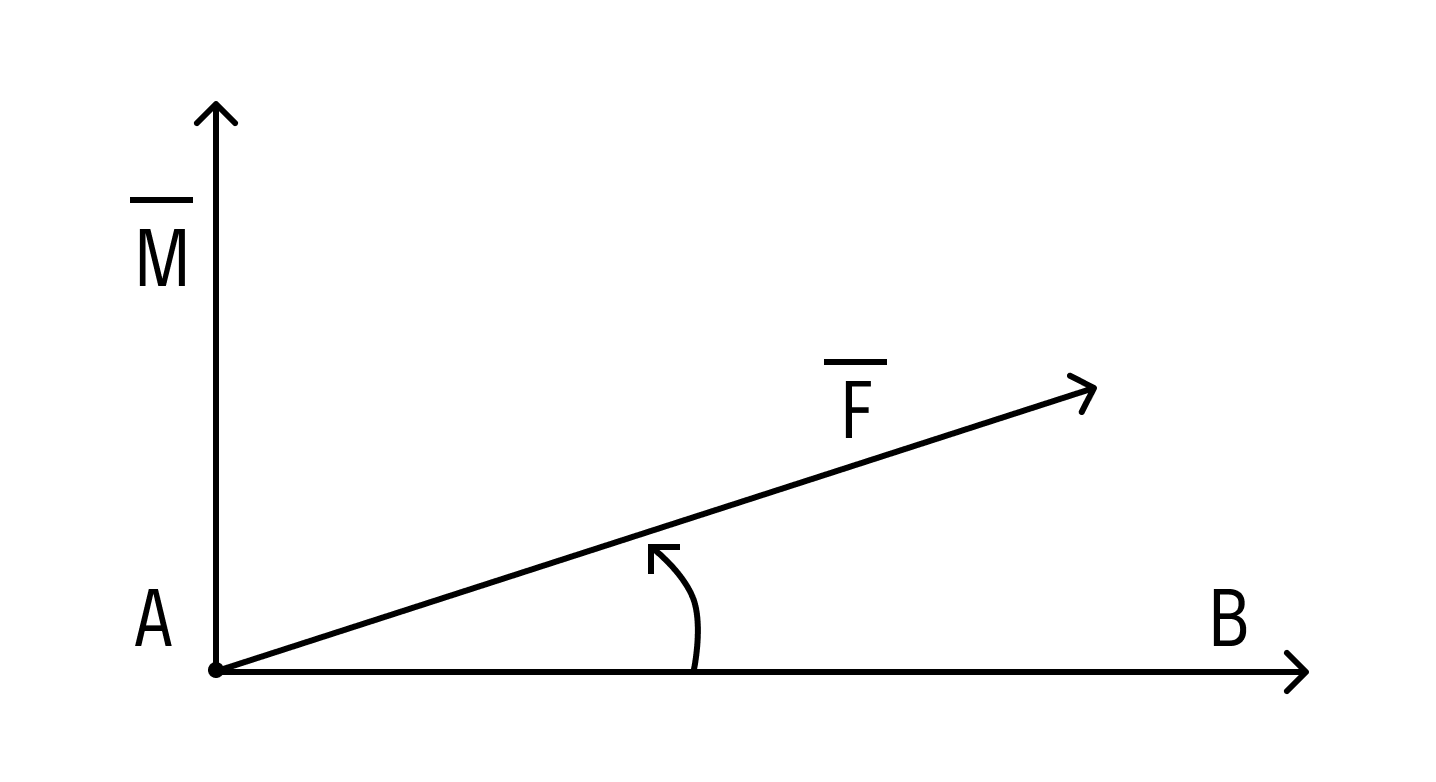
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.

Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].

Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.

Векторное произведение — определения, свойства, формулы, примеры и решения

Определение векторного произведения

Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a → , b → , c → в трехмерном пространстве.

Отложим для начала векторы a → , b → , c → от одной точки. Ориентация тройки a → , b → , c → бывает правой или левой, в зависимости от направления самого вектора c → . От того, в какую сторону осуществляется кратчайший поворот от вектора a → к b → с конца вектора c → , будет определен вид тройки a → , b → , c → .

Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a → , b → , c → называется правой, если по часовой стрелке – левой.

Далее возьмем два не коллинеарных вектора a → и b → . Отложим затем от точки A векторы A B → = a → и A C → = b → . Построим вектор A D → = c → , который одновременно перпендикулярный одновременно и A B → и A C → . Таким образом, при построении самого вектора A D → = c → мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).

Упорядоченная тройка векторов a → , b → , c → может быть, как мы выяснили правой или левой в зависимости от направления вектора.

Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.

Векторным произведением двух векторов a → и b → будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:

• если векторы a → и b → коллинеарны, он будет нулевым;
• он будет перпендикулярен и вектору a → ​​​​ и вектору b → т.е. ∠ a → c → = ∠ b → c → = π 2 ;
• его длина определяется по формуле: c → = a → · b → · sin ∠ a → , b → ;
• тройка векторов a → , b → , c → имеет такую же ориентацию, что и заданная система координат.

Векторное произведение векторов a → и b → имеет следущее обозначение: a → × b → .

Координаты векторного произведения

Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.

В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a → = ( a x ; a y ; a z ) и b → = ( b x ; b y ; b z ) называют вектор c → = a → × b → = ( a y · b z — a z · b y ) · i → + ( a z · b x — a x · b z ) · j → + ( a x · b y — a y · b x ) · k → , где i → , j → , k → являются координатными векторами.

Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i → , j → , k → , вторая строка содержит координаты вектора a → , а третья – координаты вектора b → в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Разложив данный определитель по элементам первой строки, получим равенство: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k → = = a → × b → = ( a y · b z — a z · b y ) · i → + ( a z · b x — a x · b z ) · j → + ( a x · b y — a y · b x ) · k →

Свойства векторного произведения

Известно, что векторное произведение в координатах представляется как определитель матрицы c → = a → × b → = i → j → k → a x a y a z b x b y b z , то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:

1. антикоммутативность a → × b → = — b → × a → ;
2. дистрибутивность a ( 1 ) → + a ( 2 ) → × b = a ( 1 ) → × b → + a ( 2 ) → × b → или a → × b ( 1 ) → + b ( 2 ) → = a → × b ( 1 ) → + a → × b ( 2 ) → ;
3. ассоциативность λ · a → × b → = λ · a → × b → или a → × ( λ · b → ) = λ · a → × b → , где λ — произвольное действительное число.

Данные свойства имеют не сложные доказательства.

Для примера можем доказать свойство антикоммутативности векторного произведения.

По определению a → × b → = i → j → k → a x a y a z b x b y b z и b → × a → = i → j → k → b x b y b z a x a y a z . А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно, a → × b → = i → j → k → a x a y a z b x b y b z = — i → j → k → b x b y b z a x a y a z = — b → × a → , что и доказывает антикоммутативность векторного произведения.

Векторное произведение – примеры и решения

В большинстве случаев встречаются три типа задач.

В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулой c → = a → · b → · sin ∠ a → , b → .

Найдите длину векторного произведения векторов a → и b → , если известно a → = 3 , b → = 5 , ∠ a → , b → = π 4 .

С помощью определения длины векторного произведения векторов a → и b → решим данную задач: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a → = ( a x ; a y ; a z ) и b → = ( b x ; b y ; b z ) .

Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a → и b → , а их разложения по координатным векторам вида b → = b x · i → + b y · j → + b z · k → и c → = a → × b → = ( a y · b z — a z · b y ) · i → + ( a z · b x — a x · b z ) · j → + ( a x · b y — a y · b x ) · k → , или векторы a → и b → могут быть заданы координатами точек их начала и конца.

Рассмотрим следующие примеры.

В прямоугольной системе координат заданы два вектора a → = ( 2 ; 1 ; — 3 ) , b → = ( 0 ; — 1 ; 1 ) . Найдите их векторное произведение.

По второму определению найдем векторное произведение двух векторов в заданных координатах: a → × b → = ( a y · b z — a z · b y ) · i → + ( a z · b x — a x · b z ) · j → + ( a x · b y — a y · b x ) · k → = = ( 1 · 1 — ( — 3 ) · ( — 1 ) ) · i → + ( ( — 3 ) · 0 — 2 · 1 ) · j → + ( 2 · ( — 1 ) — 1 · 0 ) · k → = = — 2 i → — 2 j → — 2 k → .

Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 — 3 0 — 1 1 = — 2 i → — 2 j → — 2 k → .

Ответ: a → × b → = — 2 i → — 2 j → — 2 k → .

Найдите длину векторного произведения векторов i → — j → и i → + j → + k → , где i → , j → , k → — орты прямоугольной декартовой системы координат.

Для начала найдем координаты заданного векторного произведения i → — j → × i → + j → + k → в данной прямоугольной системе координат.

Известно, что векторы i → — j → и i → + j → + k → имеют координаты ( 1 ; — 1 ; 0 ) и ( 1 ; 1 ; 1 ) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i → — j → × i → + j → + k → = i → j → k → 1 — 1 0 1 1 1 = — i → — j → + 2 k → .

Следовательно, векторное произведение i → — j → × i → + j → + k → имеет координаты ( — 1 ; — 1 ; 2 ) в заданной системе координат.

Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i → — j → × i → + j → + k → = — 1 2 + — 1 2 + 2 2 = 6 .

Ответ: i → — j → × i → + j → + k → = 6 . .

В прямоугольной декартовой системе координат заданы координаты трех точек A ( 1 , 0 , 1 ) , B ( 0 , 2 , 3 ) , C ( 1 , 4 , 2 ) . Найдите какой-нибудь вектор, перпендикулярный A B → и A C → одновременно.

Векторы A B → и A C → имеют следующие координаты ( — 1 ; 2 ; 2 ) и ( 0 ; 4 ; 1 ) соответственно. Найдя векторное произведение векторов A B → и A C → , очевидно, что оно является перпендикулярным вектором по определению и к A B → ​​​​​ и к A C → , то есть, является решением нашей задачи. Найдем его A B → × A C → = i → j → k → — 1 2 2 0 4 1 = — 6 i → + j → — 4 k → .

Ответ: — 6 i → + j → — 4 k → . — один из перпендикулярных векторов.

Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.

Векторы a → и b → перпендикулярны и их длины равны соответственно 3 и 4 . Найдите длину векторного произведения 3 · a → — b → × a → — 2 · b → = 3 · a → × a → — 2 · b → + — b → × a → — 2 · b → = = 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b → .

По свойству дистрибутивности векторного произведения мы можем записать 3 · a → — b → × a → — 2 · b → = 3 · a → × a → — 2 · b → + — b → × a → — 2 · b → = = 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b →

По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3 · a → × a → + 3 · a → × — 2 · b → + — b → × a → + — b → × — 2 · b → = = 3 · a → × a → + 3 · ( — 2 ) · a → × b → + ( — 1 ) · b → × a → + ( — 1 ) · ( — 2 ) · b → × b → = = 3 · a → × a → — 6 · a → × b → — b → × a → + 2 · b → × b →

Векторные произведения a → × a → и b → × b → равны 0, так как a → × a → = a → · a → · sin 0 = 0 и b → × b → = b → · b → · sin 0 = 0 , тогда 3 · a → × a → — 6 · a → × b → — b → × a → + 2 · b → × b → = — 6 · a → × b → — b → × a → . .

Из антикоммутативности векторного произведения следует — 6 · a → × b → — b → × a → = — 6 · a → × b → — ( — 1 ) · a → × b → = — 5 · a → × b → . .

Воспользовавшись свойствами векторного произведения, получаем равенство 3 · a → — b → × a → — 2 · b → = = — 5 · a → × b → .

По условию векторы a → и b → перпендикулярны, то есть угол между ними равен π 2 . Теперь остается лишь подставить найденные значения в соответствующие формулы: 3 · a → — b → × a → — 2 · b → = — 5 · a → × b → = = 5 · a → × b → = 5 · a → · b → · sin ( a → , b → ) = 5 · 3 · 4 · sin π 2 = 60 .

Ответ: 3 · a → — b → × a → — 2 · b → = 60 .

Геометрический смысл векторного произведения

Длина векторного произведения векторов по орпеделению равна a → × b → = a → · b → · sin ∠ a → , b → . Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма — удвоенного треугольника, а именно произведению сторон в виде векторов a → и b → , отложенные от одной точки, на синус угла между ними sin ∠ a → , b → .

Это и есть геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.

Под моментом силы F → , приложенной к точке B , относительно точки A будем понимать следующее векторное произведение A B → × F → .

Уравнения прямых и плоскостей

Поверхности и линии первого порядка.

Уравнение первой степени, или линейное уравнение, связывающее координаты точки в пространстве, имеет вид
$$
Ax+By+Cz+D = 0,\label
$$
причем предполагается, что коэффициенты при переменных не равны нулю одновременно, то есть \(A^<2>+B^<2>+C^ <2>\neq 0\). Аналогично, линейное уравнение, связывающее координаты точки на плоскости, — это уравнение
$$
Ax+By+C = 0,\label
$$
при условии \(A^<2>+B^ <2>\neq 0\).

В школьном курсе доказывается, что в декартовой прямоугольной системе координат уравнения \eqref и \eqref определяют соответственно плоскость и прямую линию на плоскости. Из теорем о порядке алгебраических линий и поверхностей следует, что то же самое верно и в общей декартовой системе координат. Точнее, имеют место следующие теоремы.

В общей декартовой системе координат в пространстве каждая плоскость может быть задана линейным уравнением
$$
Ax+By+Cz+D = 0.\nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат определяет плоскость.

В общей декартовой системе координат на плоскости каждая прямая может быть задана линейным уравнением
$$
Ax+By+C = 0,\nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат на плоскости определяет прямую.

Эти теоремы полностью решают вопрос об уравнениях плоскости и прямой линии на плоскости. Однако ввиду важности этих уравнений мы рассмотрим их в других формах. При этом будут получены независимые доказательства теорем этого пункта.

Параметрические уравнения прямой и плоскости.

Мы будем предполагать, что задана декартова система координат в пространстве (или на плоскости, если мы изучаем прямую в планиметрии). Это, в частности, означает, что каждой точке сопоставлен ее радиус-вектор относительно начала координат.

Рис. 6.1

Вектор \(\overrightarrowM> = \boldsymbol-\boldsymbol_<0>\), начало которого лежит на прямой, параллелен прямой тогда и только тогда, когда \(M\) также лежит на прямой. В этом и только этом случае для точки \(M\) найдется такое число \(t\), что
$$
\boldsymbol-\boldsymbol_ <0>= t\boldsymbol.\label
$$

Наоборот, какое бы число мы ни подставили в формулу \eqref в качестве \(t\), вектор \(\boldsymbol\) в этой формуле определит некоторую точку на прямой.

Уравнение \eqref называется векторным параметрическим уравнением прямой, а переменная величина \(t\), принимающая любые вещественные значения, называется параметром.

Векторное параметрическое уравнение выглядит одинаково и в планиметрии, и в стереометрии, но при разложении по базису оно сводится к двум или трем скалярным уравнениям, смотря по тому, сколько векторов составляют базис.

Получим теперь параметрические уравнения плоскости. Обозначим через \(\boldsymbol

\) и \(\boldsymbol\) ее направляющие векторы, а через \(\boldsymbol_<0>\) — радиус-вектор ее начальной точки \(M_<0>\). Пусть точка \(M\) с радиус-вектором \(\boldsymbol\) — произвольная точка пространства (рис. 6.2).

Рис. 6.2

Вектор \(\overrightarrowM> = \boldsymbol-\boldsymbol_<0>\), начало которого лежит на плоскости, параллелен ей тогда и только тогда, когда его конец \(M\) также лежит на плоскости. Так как \(\boldsymbol

\) и \(\boldsymbol\) не коллинеарны, в этом и только этом случае \(\boldsymbol-\boldsymbol_<0>\) может быть по ним разложен. Поэтому, если точка \(M\) лежит в плоскости (и только в этом случае), найдутся такие числа \(t_<1>\) и \(t_<2>\), что
$$
\boldsymbol-\boldsymbol_ <0>= t_<1>\boldsymbol

+t_<2>\boldsymbol.\label
$$

Это уравнение называется параметрическим уравнением плоскости. Каждой точке плоскости оно сопоставляет значения двух параметров \(t_<1>\) и \(t_<2>\). Наоборот, какие бы числа мы ни подставили как значения \(t_<1>\) и \(t_<2>\), уравнение \eqref определит некоторую точку плоскости.

Пусть \((x, y, z)\) и \((x_<0>, y_<0>, z_<0>)\) — координаты точек \(M\) и \(M_<0>\) соответственно, а векторы \(\boldsymbol

\) и \(\boldsymbol\) имеют компоненты \((p_<1>, p_<2>, p_<3>)\) и \((q_<1>, q_<2>, q_<3>)\). Тогда, раскладывая по базису обе части уравнения \eqref, мы получим параметрические уравнения плоскости
$$
x-x_ <0>= t_<1>p_<1>+t_<2>q_<1>,\ y-y_ <0>= t_<1>p_<2>+t_<2>q_<2>,\ z-z_ <0>= t_<1>p_<3>+t_<2>q_<3>.\label
$$

Отметим, что начальная точка и направляющий вектор прямой образуют на ней ее внутреннюю декартову систему координат. Значение параметра \(t\), соответствующее какой-то точке, является координатой этой точки во внутренней системе координат. Точно так же на плоскости начальная точка и направляющие векторы составляют внутреннюю систему координат, а значения параметров, соответствующие точке, — это ее координаты в этой системе.

Прямая линия на плоскости.

Поэтому мы можем сформулировать следующее утверждение.

В любой декартовой системе координат на плоскости уравнение прямой с начальной точкой \(M_<0>(x_<0>, y_<0>)\) и направляющим вектором \(\boldsymbol(a_<1>, a_<2>)\) может быть записано в виде \eqref.

Уравнение \eqref линейное. Действительно, после преобразования оно принимает вид \(a_<2>x-a_<1>y+(a_<1>y_<0>-a_<2>x_<0>) = 0\), то есть \(Ax+By+C = 0\), где \(A = a_<2>\), \(B = -a_<1>\) и \(C = a_<1>y_<0>-a_<2>x_<0>\).

Вектор с координатами \((-B, A)\) можно принять за направляющий вектор прямой с уравнением \eqref в общей декартовой системе координат, а точку \eqref за начальную точку.

Если система координат декартова прямоугольная, то вектор \(\boldsymbol(A, B)\) перпендикулярен прямой с уравнением \eqref.

Действительно, в этом случае \((\boldsymbol, \boldsymbol) = -BA+AB = 0\).

Пусть в уравнении прямой \(Ax+By+C = 0\) коэффициент \(B\) отличен от нуля. Это означает, что отлична от нуля первая компонента направляющего вектора, и прямая не параллельна оси ординат. В этом случае уравнение прямой можно представить в виде
$$
y = kx+b,\label
$$
где \(k = -A/B\), а \(b = -C/B\). Мы видим, что к равно отношению компонент направляющего вектора: \(k = a_<2>/a_<1>\) (рис. 6.3).

Рис. 6.3. k=-1. Прямая y=-x+1/2

Отношение компонент направляющего вектора \(a_<2>/a_<1>\) называется угловым коэффициентом прямой.

Угловой коэффициент прямой в декартовой прямоугольной системе координат равен тангенсу угла, который прямая образует с осью абсцисс. Угол этот отсчитывается от оси абсцисс в направлении кратчайшего поворота от \(\boldsymbol_<1>\) к \(\boldsymbol_<2>\) (рис. 6.4).

Рис. 6.4. \(k=\operatorname\varphi = -1\). Прямая \(y=-x+1/2\)

Положив \(x = 0\) в уравнении \eqref, получаем \(y = b\). Это означает, что свободный член уравнения \(b\) является ординатой точки пересечения прямой с осью ординат.

Если же в уравнении прямой \(B = 0\) и ее уравнение нельзя представить в виде \eqref, то обязательно \(A \neq 0\). В этом случае прямая параллельна оси ординат и ее уравнению можно придать вид \(x = x_<0>\), где \(x_ <0>= -C/A\) — абсцисса точки пересечения прямой с осью абсцисс.

Векторные уравнения плоскости и прямой.

Параметрическое уравнение плоскости утверждает, что точка \(M\) лежит на плоскости тогда и только тогда, когда разность ее радиус-вектора и радиус-вектора начальной точки \(M_<0>\) компланарна направляющим векторам \(\boldsymbol

\) и \(\boldsymbol\). Эту компланарность можно выразить и равенством
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol

, \boldsymbol) = 0.\label
$$
Вектор \(\boldsymbol = [\boldsymbol

, \boldsymbol]\) — ненулевой вектор, перпендикулярный плоскости. Используя его, мы можем записать уравнение \eqref в виде
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol) = 0.\label
$$

Уравнения \eqref и \eqref называют векторными уравнениями плоскости. Им можно придать форму, в которую не входит радиус-вектор начальной точки. Например, положив в \eqref \(D = -(\boldsymbol_<0>, \boldsymbol)\), получим
$$
(\boldsymbol, \boldsymbol)+D = 0.\label
$$

Для прямой на плоскости можно также написать векторные уравнения, аналогичные \eqref и \eqref,
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol) = 0\ \mbox<или>\ (\boldsymbol, \boldsymbol)+C = 0.\nonumber
$$
Первое из них выражает тот факт, что вектор \(\boldsymbol-\boldsymbol_<0>\) перпендикулярен ненулевому вектору \(\boldsymbol\), перпендикулярному направляющему вектору \(\boldsymbol\), и потому коллинеарен \(\boldsymbol\).

Пусть \(x, y, z\) — компоненты вектора \(\boldsymbol\) в общей декартовой системе координат. Тогда скалярное произведение \((\boldsymbol-\boldsymbol_<0>, \boldsymbol)\) при \(\boldsymbol \neq 0\) записывается линейным многочленом \(Ax+By+Cz+D\), где \((A^<2>+B^<2>+C^ <2>\neq 0)\).

Обратно, для любого линейного многочлена найдутся такие векторы \(\boldsymbol_<0>\) и \(\boldsymbol \neq 0\), что в заданной общей декартовой системе координат \(Ax+By+Cz+D = (\boldsymbol-\boldsymbol_<0>, \boldsymbol)\).

Первая часть предложения очевидна: подставим разложение вектора \(\boldsymbol\) по базису в данное скалярное произведение:
$$
(x\boldsymbol_<1>+y\boldsymbol_<2>+z\boldsymbol_<3>-\boldsymbol_<0>, \boldsymbol),\nonumber
$$
раскроем скобки и получим многочлен \(Ax+By+Cz+D\), в котором \(D = -(\boldsymbol_<0>, \boldsymbol)\) и
$$
A = (\boldsymbol_<1>, \boldsymbol),\ B = (\boldsymbol_<2>, \boldsymbol),\ C = (\boldsymbol_<3>, \boldsymbol)\label
$$
\(A\), \(B\) и \(C\) одновременно не равны нулю, так как ненулевой вектор \(\boldsymbol\) не может быть ортогонален всем векторам базиса.

Для доказательства обратного утверждения найдем сначала вектор \(\boldsymbol\) из равенств \eqref, считая \(A\), \(B\) и \(C\) заданными. Из ранее доказанного утверждения 10 следует, что
$$
\boldsymbol = \frac_<2>, \boldsymbol_<3>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>+\frac_<3>, \boldsymbol_<1>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>+\frac_<1>, \boldsymbol_<2>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>.\label
$$

Вектор \(\boldsymbol_<0>\) должен удовлетворять условию \(D = -(\boldsymbol_<0>, \boldsymbol)\). Один из таких векторов можно найти в виде \(\boldsymbol_ <0>= \lambda \boldsymbol\). Подставляя, видим, что \(-\lambda(\boldsymbol, \boldsymbol) = D\), откуда \(\boldsymbol_ <0>= -D\boldsymbol/|\boldsymbol|^<2>\).

Итак, мы нашли векторы \(\boldsymbol\) и \(\boldsymbol_<0>\) такие, что линейный многочлен записывается в виде
$$
x(\boldsymbol_<1>, \boldsymbol)+y(\boldsymbol_<2>, \boldsymbol)+z(\boldsymbol_<3>, \boldsymbol)-(\boldsymbol_<0>, \boldsymbol),\nonumber
$$
который совпадает с требуемым \((\boldsymbol-\boldsymbol_<0>, \boldsymbol)\).

Если система координат декартова прямоугольная, то вектор с компонентами \(A\), \(B\), \(C\) является нормальным вектором для плоскости с уравнением \(Ax+By+Cz+D = 0\).

Это сразу вытекает из формул \eqref и доказанного ранее утверждения о нахождении компонент в ортогональном базисе.

Любые два неколлинеарных вектора, удовлетворяющие уравнению \eqref, можно принять за направляющие векторы плоскости.

Утверждение 5 нетрудно доказать и непосредственно, рассматривая координаты вектора, параллельного плоскости, как разности соответствующих координат двух точек, лежащих в плоскости.

Все, сказанное о плоскостях, почти без изменений может быть сказано и о прямых на плоскости. В частности, верно следующее утверждение.

Действительно, \(\alpha_<1>, \alpha_<2>\), должны быть пропорциональны компонентам — \(B\), \(A\) направляющего вектора прямой.

Параллельность плоскостей и прямых на плоскости.

Ниже, говоря о параллельных прямых или плоскостях, мы будем считать, что параллельные плоскости (или прямые) не обязательно различны, то есть что плоскость (прямая) параллельна самой себе.

Прямые линии, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+C = 0,\ A_<1>x+B_<1>y+C_ <1>= 0,\nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число \(\lambda\), что
$$
A_ <1>= \lambda A,\ B_ <1>= \lambda B.\label
$$

Прямые совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнения \eqref выполнено (с тем же \(\lambda\)) равенство
$$
C_ <1>= \lambda C.\label
$$

Первая часть предложения прямо следует из того, что векторы с компонентами \((-B, A)\) и \((-B_<1>, A_<1>)\) — направляющие векторы прямых.

Докажем вторую часть. В равенствах \eqref и \eqref \(\lambda \neq 0\), так как коэффициенты в уравнении прямой одновременно нулю не равны. Поэтому, если эти равенства выполнены, уравнения эквивалентны и определяют одну и ту же прямую.

Обратно, пусть прямые параллельны. В силу первой части предложения их уравнения должны иметь вид \(Ax+By+C = 0\) и \(\lambda(Ax+By)+C_ <1>= 0\) при некотором \(\lambda\). Если, кроме того, существует общая точка \(M_<0>(x_<0>, y_<0>)\) обеих прямых, то \(Ax_<0>+By_<0>+C = 0\) и \(\lambda(Ax_<0>+By_<0>)+C_ <1>= 0\). Вычитая одно равенство из другого, получаем \(C_ <1>= \lambda C\), как и требовалось.

Плоскости, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+Cz+D = 0,\ A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0\nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число \(\lambda\), что
$$
A_ <1>= \lambda A,\ B_ <1>= \lambda B,\ C_ <1>= \lambda C.\label
$$

Плоскости совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнений \eqref выполнено (с тем же \(\lambda\)) равенство
$$
D_ <1>= \lambda D.\label
$$

Если плоскости параллельны, то их нормальные векторы \(\boldsymbol\) и \(\boldsymbol_<1>\) коллинеарны, и существует такое число \(\lambda\), что \(\boldsymbol_ <1>= \lambda\boldsymbol\). В силу уравнений \eqref \(A_ <1>= (\boldsymbol_<1>, \boldsymbol_<1>) = \lambda(\boldsymbol_<1>, \boldsymbol) = \lambda A\). Аналогично доказываются и остальные равенства \eqref. Обратно, если равенства \eqref выполнены, то из формулы \eqref следует, что \(\boldsymbol_ <1>= \lambda\boldsymbol\). Это доказывает первую часть предложения. Вторая его часть доказывается так же, как вторая часть предложения 7.

Условия \eqref выражают не что иное, как коллинеарность векторов с компонентами \((A, B)\) и \((A_<1>, B_<1>)\). Точно так же условия \eqref означают коллинеарность векторов с компонентами \((A, B, C)\) и \((A_<1>, B_<1>, C_<1>)\). Поэтому согласно ранее доказанным этому и этому утверждениям условие параллельности прямых на плоскости можно записать в виде
$$
\begin
A& B\\
A_<1>& B_<1>
\end
= 0,\label
$$
а условие параллельности плоскостей — в виде
$$
\begin
B& C\\
B_<1>& C_<1>
\end =
\begin
C& A\\
C_<1>& A_<1>
\end =
\begin
A& B\\
A_<1>& B_<1>
\end
= 0.\label
$$

Утверждению 7 можно придать чисто алгебраическую формулировку, если учесть, что координаты точки пересечения прямых — это решение системы, составленной из их уравнений.

При условии \eqref система линейных уравнений
$$
Ax+By+C = 0,\ A_<1>x+B_<1>y+C_ <1>= 0,\nonumber
$$
не имеет решений или имеет бесконечно много решений (в зависимости от \(C\) и \(C_<1>\). В последнем случае система равносильна одному из составляющих ее уравнений. Если же
$$
\begin
A& B\\
A_<1>& B_<1>
\end
\neq 0.\nonumber
$$
то при любых \(C\) и \(C_<1>\) система имеет единственное решение \((x, y)\).

Уравнения прямой в пространстве.

Прямая линия в пространстве может быть задана как пересечение двух плоскостей и, следовательно, в общей декартовой системе координат определяется системой уравнений вида
$$
\left\<\begin
Ax+By+Cz+D = 0,\\
A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0.
\end\right.\label
$$
Пересечение плоскостей — прямая линия тогда и только тогда, когда они не параллельны, что согласно \eqref означает, что хоть один из детерминантов отличен от нуля:
$$
\begin
B& C\\
B_<1>& C_<1>
\end^ <2>+
\begin
C& A\\
C_<1>& A_<1>
\end^ <2>+
\begin
A& B\\
A_<1>& B_<1>
\end^<2>
\neq 0.\label
$$

Разумеется, систему \eqref можно заменить на любую, ей эквивалентную. При этом прямая будет представлена как пересечение двух других проходящих через нее плоскостей.

Вспомним параметрические уравнения прямой \eqref. Допустим, что в них ни одна из компонент направляющего вектора не равна нулю. Тогда
$$
t = \frac><\alpha_<1>>,\ t = \frac><\alpha_<2>>,\ t = \frac><\alpha_<3>>,\nonumber
$$
и мы получаем два равенства
$$
\frac><\alpha_<2>> = \frac><\alpha_<3>>,\ \frac><\alpha_<1>> = \frac><\alpha_<3>>,\label
$$
или, в более симметричном виде,
$$
\frac><\alpha_<1>> = \frac><\alpha_<2>> = \frac><\alpha_<3>>,\label
$$
Уравнения \eqref представляют прямую как линию пересечения двух плоскостей, первая из которых параллельна оси абсцисс (в ее уравнение не входит переменная \(x\)), а вторая параллельна оси ординат.

Если обращается в нуль одна из компонент направляющего вектора, например, \(\alpha_<1>\), то уравнения прямой принимают вид
$$
x = x_<0>,\ \frac><\alpha_<2>> = \frac><\alpha_<3>>,\label
$$
Эта прямая лежит в плоскости \(x = x_<0>\) и, следовательно, параллельна плоскости \(x = 0\). Аналогично пишутся уравнения прямой, если в нуль обращается не \(\alpha_<1>\), а другая компонента.

Когда равны нулю две компоненты направляющего вектора, например, \(\alpha_<1>\) и \(\alpha_<2>\), то прямая имеет уравнения
$$
x = x_<0>,\ y = y_<0>.\label
$$
Такая прямая параллельна одной из осей координат, в нашем случае — оси аппликат.

Важно уметь находить начальную точку и направляющий вектор прямой, заданной системой линейных уравнений \eqref. По условию \eqref один из детерминантов отличен от нуля. Допустим для определенности, что \(AB_<1>-A_<1>B \neq 0\). В силу утверждения 9 при любом фиксированном \(z\) система уравнений будет иметь единственное решение \((x, y)\), в котором \(x\) и \(y\), разумеется, зависят от \(z\). Они — линейные многочлены от \(z\): \(x = \alpha_<1>z+\beta_<1>\), \(y = \alpha_<2>z+\beta_<2>\).

Не будем доказывать этого, хотя это и не трудно сделать. Для ясности, заменяя \(z\) на \(t\), получаем параметрические уравнения прямой
$$
x = \alpha_<1>t+\beta_<1>,\ y = \alpha_<2>t+\beta_<2>,\ z = t.\nonumber
$$

Первые две координаты начальной точки прямой \(M_<0>(\beta_<1>, \beta_<2>, 0)\) можно получить, решая систему \eqref при значении \(z = 0\).

Из параметрических уравнений видно, что в этом случае направляющий вектор имеет координаты \((\alpha_<1>, \alpha_<2>, 1)\). Найдем его компоненты в общем виде. Если система координат декартова прямоугольная, векторы с компонентами \((A, B, C)\) и \(A_<1>, B_<1>, C_<1>\) перпендикулярны соответствующим плоскостям, а потому их векторное произведение параллельно прямой \eqref, по которой плоскости пересекаются. Вычисляя векторное произведение в ортонормированном базисе, мы получаем компоненты направляющего вектора
$$
\begin
B& C\\
B_<1>& C_<1>
\end,\
\begin
C& A\\
C_<1>& A_<1>
\end,\
\begin
A& B\\
A_<1>& B_<1>
\end.\label
$$

Вектор с компонентами \eqref есть направляющий вектор прямой с уравнениями \eqref, какова бы ни была декартова система координат.

Согласно утверждению 5 каждый ненулевой вектор, компоненты которого \((\alpha_<1>, \alpha_<2>, \alpha_<3>)\) удовлетворяют уравнению \(A\alpha_<1>+B\alpha_<2>+C\alpha_ <3>= 0\), параллелен плоскости с уравнением \(Ax+By+Cz+D = 0\). Если, кроме того, он удовлетворяет уравнению \(A_<1>\alpha_<1>+B_<1>\alpha_<2>+C_<1>\alpha_ <3>= 0\), то он параллелен и второй плоскости, то есть может быть принят за направляющий вектор прямой. Вектор с компонентами \eqref ненулевой в силу неравенства \eqref. Непосредственно легко проверить, что его компоненты удовлетворяют обоим написанным выше условиям. На этом доказательство заканчивается.