Решения задач: метод наименьших квадратов
Метод наименьших квадратов применяется для решения различных математических задач и основан на минимизации суммы квадратов отклонений функций от исходных переменных. Мы рассмотриваем его приложение к математической статистике в простейшем случае, когда нужно найти зависимость (парную линейную регрессию) между двумя переменными, заданными выборочными данным. В этом случае речь идет об отклонениях теоретических значений от экспериментальных.
Краткая инструкция по методу наименьших квадратов для чайников: определяем вид предполагаемой зависимости (чаще всего берется линейная регрессия вида $y(x)=ax+b$), выписываем систему уравнений для нахождения параметров $a, b$. По экспериментальным данным проводим вычисления и подставляем значения в систему, решаем систему любым удобным методом (для размерности 2-3 можно и вручную). Получается искомое уравнение.
Иногда дополнительно к нахождению уравнения регрессии требуется: найти остаточную дисперсию, сделать прогноз значений, найти значение коэффициента корреляции, проверить качество аппроксимации и значимость модели. Примеры решений вы найдете ниже. Удачи в изучении!
Примеры решений МНК
Пример 1. Методом наименьших квадратов для данных, представленных в таблице, найти линейную зависимость
Пример 2. Прибыль фирмы за некоторый период деятельности по годам приведена ниже:
Год 1 2 3 4 5
Прибыль 3,9 4,9 3,4 1,4 1,9
1) Составьте линейную зависимость прибыли по годам деятельности фирмы.
2) Определите ожидаемую прибыль для 6-го года деятельности. Сделайте чертеж.
Пример 3. Экспериментальные данные о значениях переменных х и y приведены в таблице:
1 2 4 6 8
3 2 1 0,5 0
В результате их выравнивания получена функция Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
Пример 4. Данные наблюдений над случайной двумерной величиной (Х, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X.
Пример 5. Считая, что зависимость между переменными x и y имеет вид $y=ax^2+bx+c$, найти оценки параметров a, b и c методом наименьших квадратов по выборке:
x 7 31 61 99 129 178 209
y 13 10 9 10 12 20 26
Пример 6. Проводится анализ взаимосвязи количества населения (X) и количества практикующих врачей (Y) в регионе.
Годы 81 82 83 84 85 86 87 88 89 90
X, млн. чел. 10 10,3 10,4 10,55 10,6 10,7 10,75 10,9 10,9 11
Y, тыс. чел. 12,1 12,6 13 13,8 14,9 16 18 20 21 22
Оцените по МНК коэффициенты линейного уравнения регрессии $y=b_0+b_1x$.
Существенно ли отличаются от нуля найденные коэффициенты?
Проверьте значимость полученного уравнения при $\alpha = 0,01$.
Если количество населения в 1995 году составит 11,5 млн. чел., каково ожидаемое количество врачей? Рассчитайте 99%-й доверительный интервал для данного прогноза.
Рассчитайте коэффициент детерминации
Метод наименьших квадратов
Начнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – x и y . Занесем их в таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | |
| x i | 0 | 1 | 2 | 4 | 5 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 , 0 |
После выравнивания получим функцию следующего вида: g ( x ) = x + 1 3 + 1 .
Мы можем аппроксимировать эти данные с помощью линейной зависимости y = a x + b , вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные.
В чем именно заключается МНК (метод наименьших квадратов)
Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 будет наименьшим. Иначе говоря, при определенных значениях a и b сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных.
Как вывести формулы для вычисления коэффициентов
Для того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 по a и b и приравниваем их к 0 .
δ F ( a , b ) δ a = 0 δ F ( a , b ) δ b = 0 ⇔ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i = 0 — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) = 0 ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + ∑ i = 1 n b = ∑ i = 1 n y i ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + n b = ∑ i = 1 n y i
Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов.
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n
Мы вычислили значения переменных, при который функция
F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 примет минимальное значение. В третьем пункте мы докажем, почему оно является именно таким.
Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра a , включает в себя ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 , а также параметр
n – им обозначено количество экспериментальных данных. Советуем вам вычислять каждую сумму отдельно. Значение коэффициента b вычисляется сразу после a .
Обратимся вновь к исходному примеру.
Здесь у нас n равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | ∑ i = 1 5 | |
| x i | 0 | 1 | 2 | 4 | 5 | 12 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x i y i | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x i 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Решение
Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного i . Пятая строка содержит данные из второй, возведенные в квадрат. В последнем столбце приводятся суммы значений отдельных строчек.
Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты a и b . Для этого подставим нужные значения из последнего столбца и подсчитаем суммы:
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n ⇒ a = 5 · 33 , 8 — 12 · 12 , 9 5 · 46 — 12 2 b = 12 , 9 — a · 12 5 ⇒ a ≈ 0 , 165 b ≈ 2 , 184
У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как y = 0 , 165 x + 2 , 184 . Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – g ( x ) = x + 1 3 + 1 или 0 , 165 x + 2 , 184 . Произведем оценку с помощью метода наименьших квадратов.
Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 и σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 , минимальное значение будет соответствовать более подходящей линии.
σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 = = ∑ i = 1 5 ( y i — ( 0 , 165 x i + 2 , 184 ) ) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 = = ∑ i = 1 5 ( y i — ( x i + 1 3 + 1 ) ) 2 ≈ 0 , 096
Ответ: поскольку σ 1 σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0 , 165 x + 2 , 184 .
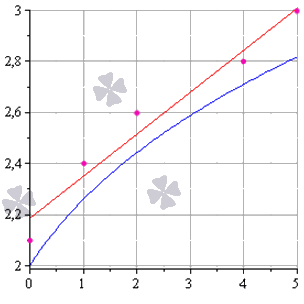
Как изобразить МНК на графике функций
Метод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая g ( x ) = x + 1 3 + 1 , синей – y = 0 , 165 x + 2 , 184 . Исходные данные обозначены розовыми точками.
Поясним, для чего именно нужны приближения подобного вида.
Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при x = 3 или при x = 6 . Таким примерам мы посвятили отдельную статью.
Доказательство метода МНК
Чтобы функция приняла минимальное значение при вычисленных a и b , нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 была положительно определенной. Покажем, как это должно выглядеть.
У нас есть дифференциал второго порядка следующего вида:
d 2 F ( a ; b ) = δ 2 F ( a ; b ) δ a 2 d 2 a + 2 δ 2 F ( a ; b ) δ a δ b d a d b + δ 2 F ( a ; b ) δ b 2 d 2 b
Решение
δ 2 F ( a ; b ) δ a 2 = δ δ F ( a ; b ) δ a δ a = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ a = 2 ∑ i = 1 n ( x i ) 2 δ 2 F ( a ; b ) δ a δ b = δ δ F ( a ; b ) δ a δ b = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ b = 2 ∑ i = 1 n x i δ 2 F ( a ; b ) δ b 2 = δ δ F ( a ; b ) δ b δ b = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) δ b = 2 ∑ i = 1 n ( 1 ) = 2 n
Иначе говоря, можно записать так: d 2 F ( a ; b ) = 2 ∑ i = 1 n ( x i ) 2 d 2 a + 2 · 2 ∑ x i i = 1 n d a d b + ( 2 n ) d 2 b .
Мы получили матрицу квадратичной формы вида M = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .
В этом случае значения отдельных элементов не будут меняться в зависимости от a и b . Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными.
Вычисляем угловой минор первого порядка: 2 ∑ i = 1 n ( x i ) 2 > 0 . Поскольку точки x i не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах.
Вычисляем угловой минор второго порядка:
d e t ( M ) = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2
После этого переходим к доказательству неравенства n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 с помощью математической индукции.
- Проверим, будет ли данное неравенство справедливым при произвольном n . Возьмем 2 и подсчитаем:
2 ∑ i = 1 2 ( x i ) 2 — ∑ i = 1 2 x i 2 = 2 x 1 2 + x 2 2 — x 1 + x 2 2 = = x 1 2 — 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
У нас получилось верное равенство (если значения x 1 и x 2 не будут совпадать).
- Сделаем предположение, что данное неравенство будет верным для n , т.е. n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 – справедливо.
- Теперь докажем справедливость при n + 1 , т.е. что ( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 > 0 , если верно n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 .
( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 = = ( n + 1 ) ∑ i = 1 n ( x i ) 2 + x n + 1 2 — ∑ i = 1 n x i + x n + 1 2 = = n ∑ i = 1 n ( x i ) 2 + n · x n + 1 2 + ∑ i = 1 n ( x i ) 2 + x n + 1 2 — — ∑ i = 1 n x i 2 + 2 x n + 1 ∑ i = 1 n x i + x n + 1 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + n · x n + 1 2 — x n + 1 ∑ i = 1 n x i + ∑ i = 1 n ( x i ) 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + x n + 1 2 — 2 x n + 1 x 1 + x 1 2 + + x n + 1 2 — 2 x n + 1 x 2 + x 2 2 + . . . + x n + 1 2 — 2 x n + 1 x 1 + x n 2 = = n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + + ( x n + 1 — x 1 ) 2 + ( x n + 1 — x 2 ) 2 + . . . + ( x n — 1 — x n ) 2 > 0
Выражение, заключенное в фигурные скобки, будет больше 0 (исходя из того, что мы предполагали в пункте 2 ), и остальные слагаемые будут больше 0 , поскольку все они являются квадратами чисел. Мы доказали неравенство.
Ответ: найденные a и b будут соответствовать наименьшему значению функции F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 , значит, они являются искомыми параметрами метода наименьших квадратов (МНК).
Метод наименьших квадратов
Метод наименьших квадратов (МНК) — это статистическая процедура для довольно точного прогнозирования поведения зависимых переменных.
Например, можно понять, как будет меняться товарооборот (значение «y») сети магазинов с изменением размеров торговой площади (значение «x»).
Суть МНК — из всех линейных функций найти наилучшее приближение к реальности. Это можно сделать путём поиска функции с наименьшим отклонением (точнее по процессу МНК: поиск минимальной суммы квадратов отклонений значений y (игрек) от полученного уравнения регрессии).
Решение МНК
Мы ищем уравнение линейной регрессии, которое выглядит так: y = ax + b
- y – зависимая переменная
- x – независимая переменная
- a – коэффициент (это также наклон/градиент линии)
- b – коэффициент (это также точка, где линия пересекает ось Y)
Метод 1
Шаги, которые мы будем делать для поиска y = ax + b (сейчас мы их все пройдём на примере):
Шаг 1: Для каждой точки (x, y) вычислить x² и xy.
Шаг 2: Суммировать все x, y, x² и xy, это даст нам Σx, Σy, Σx² и Σxy (если кто забыл, Σ означает «сумма»).
Шаг 3: Рассчитать наклон a по этой формуле:
, где N – количество данных
Шаг 4: Рассчитать значение числа b:
, где N – количество данных
Шаг 5: Подставить найденные числа по местам в уравнение (y = ax + b)
Пример
После некоторых наблюдений, у нас появились данные о размерах и продажах некой торговой сети, у которой 5 магазинов:
| Размер (x) | Продажи (y) |
|---|---|
| 2 | 4 |
| 3 | 6 |
| 5 | 8 |
| 7 | 10 |
| 9 | 12 |
Для наглядности, например, это магазины мороженого, и 2-метровая лавочка продаёт в месяц 4 тонны мороженого, 7 метровая — 10 тонн.
Сразу можно записать, что N = 5 (количество данных; т.е. всего у нас данные по пяти магазинам, ведь у нас 5 строк данных).
Для каждой точки (x, y) вычисляем x² и xy. Для этого, к уже существующим столбцам добавим ещё два: x² и xy.
- x² получим путём возведения x (Размер) в квадрат
- xy получим путём умножения одного на второе
| x | y | x² | xy |
|---|---|---|---|
| 2 | 4 | 2² = 4 | 2 × 4 = 8 |
| 3 | 6 | 3² = 9 | 3 × 6 = 18 |
| 5 | 8 | 25 | 40 |
| 7 | 10 | 49 | 70 |
| 9 | 12 | 81 | 108 |
Шаг 2: Суммировать все x, y, x² и xy, это даст нам Σx, Σy, Σx² и Σxy (складываем каждый столбик):
| x | y | x² | xy |
|---|---|---|---|
| 2 | 4 | 2² = 4 | 2 × 4 = 8 |
| 3 | 6 | 3² = 9 | 3 × 6 = 18 |
| 5 | 8 | 25 | 40 |
| 7 | 10 | 49 | 70 |
| 9 | 12 | 81 | 108 |
| Σx = 26 | Σy = 40 | Σx² = 168 | Σxy = 244 |
Шаг 3: Рассчитать a (наклон графика) по этой формуле:
, где N – количество данных
Помним, что N = 5, значит:
Шаг 4: Рассчитать значение числа b:
, где N – количество данных
Помним, что N = 5, значит:
Шаг 5: Подставить найденные числа по местам в уравнение
y = ax + b ⇒ y = 1,0976x + 2,29248
Далее можем проверить. Можем составить вот такой график, вместе с данными точками и полученной функцией:
Также мы можем использовать эту функцию, чтобы понять, как будут зависеть продажи фирмы от размера помещения. Например: руководство хочет открыть магазин размером в 11,5 м². Для этого подставляем 11,5 вместо x:
y = 1,0976x + 2,29248 ⇒ y = 1,0976 × 11,5 + 2,29248 = 14,91488
Ответ: этот магазин размером в 11,5 м² будет продавать около 15 тонн мороженого в месяц.
Метод 2
Мы продолжаем искать уравнение линейной регрессии, которое выглядит так: y = ax + b.
Используем тот же пример с сетью магазинов.
| Размер (x) | Продажи (y) |
|---|---|
| 2 | 4 |
| 3 | 6 |
| 5 | 8 |
| 7 | 10 |
| 9 | 12 |
Шаг 1: Опять суммируем все x, y, x² и xy, т.е. находим Σx, Σy, Σx² и Σxy (складываем каждый столбик):
| x | y | x² | xy |
|---|---|---|---|
| 2 | 4 | 2² = 4 | 2 × 4 = 8 |
| 3 | 6 | 3² = 9 | 3 × 6 = 18 |
| 5 | 8 | 25 | 40 |
| 7 | 10 | 49 | 70 |
| 9 | 12 | 81 | 108 |
| Σx = 26 | Σy = 40 | Σx² = 168 | Σxy = 244 |
Шаг 2: Записать вот такую систему уравнений (так мы будем искать параметры a и b):
Шаг 3: Помним, что N = 5. Таким образом, из нашего примера получаем систему:
Лучше конечно её переписать красиво:
Шаг 4: Решить систему.
Находим a = 1,0976; b = 2,29248; и ставим по местам в функцию (y = ax + b). Получается y = 1,0976x + 2,29248
Для проверки лучше составить график с данными точками и найденной функцией, как в методе 1.
http://zaochnik.com/spravochnik/matematika/stati/metod-naimenshih-kvadratov/
http://www.uznaychtotakoe.ru/metod-naimenshih-kvadratov/