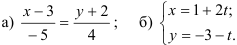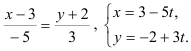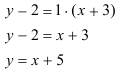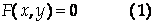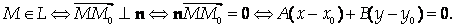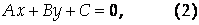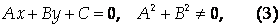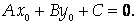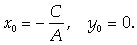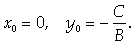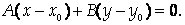Контрольная работа на тему: прямая на плоскости, кривые второго порядка
Прямая на плоскости. Кривые второго порядка
Задание: Составление уравнений прямых.
Цель: формирование умения составлять уравнения прямых на плоскости.
Задание для самостоятельной внеаудиторной работы:
7.1. Опираясь на обобщающие таблицы, изучите, какими способами можно задать прямую, и какие виды уравнения прямой существуют.
7.2. В треугольнике 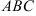
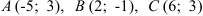
а) прямой 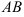
б) медианы 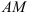
в) прямой, проходящей через точку 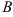
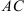
г) прямой, проходящей через точку 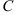
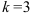
7.3. 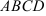
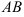
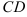
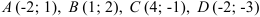
а) диагонали 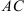
б) прямой, параллельной основаниям, проходящей через точку 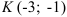
в) прямой, проходящей через точку 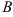
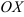
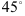
г) средней линии трапеции в каноническом виде;
д) прямой, проходящей через точку 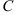
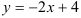
7.4. Запишите уравнение прямой во всех видах (общем, каноническом, параметрическом, с угловым коэффициентом) и постройте эту прямую:
Методические указания по выполнению работы:
Уравнением линии на плоскости называется уравнение с двумя переменными 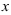
Прямые — самые простые линии на плоскости. Им соответствуют уравнения первой степени.
При решении задач удобно использовать следующие обобщающие таблицы:
Способы задания прямой

Виды уравнений прямой
Рассмотрим примеры решения типовых задач.
Пример 1.
Составьте уравнение прямой, проходящей через точку 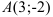
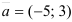
Решение:
Определим способ задания прямой: с помощью точки 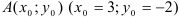
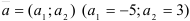
Подставим координаты точки и направляющего вектора в уравнение 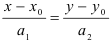
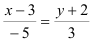
Подставим координаты точки и направляющего вектора в уравнение
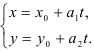
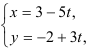
Ответ:
Пример 2.
Составьте уравнение прямой, проходящей через точки 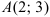
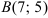
Решение:
Подставив в формулу 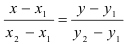
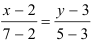
Ответ: 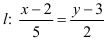
Пример 3.
Составьте уравнение прямой, проходящей через точку 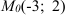
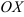
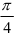
Решение:
Найдём угловой коэффициент прямой: 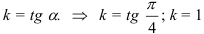
Подставим 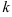
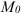
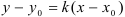
Ответ: 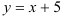
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Домашняя контрольная работа по теме уравнение прямой на плоскости
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Домашняя контрольная работа №4 « Уравнение прямой и окружности на плоскости »
1) В координатной плоскости постройте треугольник по точкам.
2) Составьте уравнения сторон, как уравнение прямой, проходящей через две точки:

3) Чтобы составить уравнение медианы АМ, нужно сначала найти координаты точки М, как середины отрезка ВС, по формулам: 

4) Уравнение высоты ВН, найдем как уравнение прямой, проходящей через точку В, перпендикулярно стороне АС. ( 



5) Составим уравнение прямой l , как уравнение прямой проходящей через точку С, параллельно вектору 




6) Пусть 






7) Уравнение окружности имеет вид: 

8) Сначала необходимо найти координаты центра, т.е середину отрезка АВ ( по формулам из пункта (в)), а затем найти радиус, как половину диаметра, т.е половину длины отрезка АВ.
Задача: Треугольник АВС, задан координатами своих вершин (по 3 балла за задание)
Постройте указанный треугольник,
Составьте уравнение стороны АВ,
Составьте уравнение медианы АМ,
Составьте уравнение высоты ВН,
Составьте уравнение прямой l , проходящей через точку С параллельно стороне АВ,
Найдите точку пересечения медианы АМ и высоты ВН
Составьте уравнение окружности с центром в точке А и проходящей через точку М,
Составьте уравнение окружности с диаметром АС,
Все точки и лини, указанные в пунктах 1 – 8 нужно указать на рисунке.
12 баллов – «3», 18 баллов – «4», 22 балла – «5».
Задачи для самостоятельного решения
4.1.1. Прямые и плоскости. Уравнение прямой на плоскости. Общее уравнение прямой на плоскости
Пусть на плоскости задана декартова прямоугольная система координат. Говорят, что соотношение (или уравнение)
Задает множество точек L на плоскости, если для любой точки М 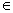
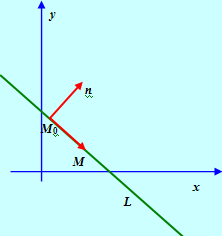
Пусть на плоскости дана точка М0 = <X0, Y0>. Найдем уравнение прямой L, проходящей через эту точку перпендикулярно вектору П = (А, В). Пусть М = <X, Y> – произвольная точка на прямой L. Тогда
Тем самым уравнение прямой L задается в виде
Нормальным вектором Прямой называется любой ненулевой вектор, перпендикулярный этой прямой.
Пример 1. Найдем уравнение прямой с нормальным вектором П = (-3, 2), проходящей через точку M0 = <2, 1>. Имеем
Теорема 9.1. Всякая прямая на плоскости может быть задана уравнением
И любое уравнение (3) задает на плоскости некоторую прямую. При этом вектор П = (А, В) является нормальным вектором этой прямой.
Пусть дана произвольная прямая. Выберем на ней точку М0 = <X0, Y0>. Пусть П = (А, В) – некоторый нормальный вектор этой прямой. Тогда, как было показано выше, уравнение этой прямой запишется в виде (3).
Покажем, что всякое уравнение (3) определяет некоторую прямую на плоскости. Найдем точку М0 = <X0, Y0>, координаты которой удовлетворяют уравнению
Если А 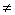
А если В 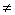
Теперь построим прямую с нормальным вектором П = (А, В), проходящую через точку М0. Ее уравнение будет иметь вид
Раскрывая скобки, приходим к уравнению (3).
Уравнение (3) называется Общим уравнением прямой На плоскости.
http://infourok.ru/domashnyaya-kontrolnaya-rabota-po-teme-uravnenie-pryamoy-na-ploskosti-2015435.html
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-i-analiticheskaia-geometriia/4-1-1-priamye-i-ploskosti-uravnenie-priamoi-na-ploskosti-obshchee-uravnenie-priamoi-na-ploskosti