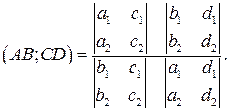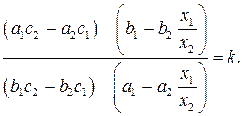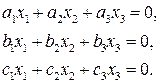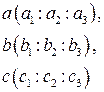Уравнение прямой на проективной плоскости

Практические задания. 1. На проективной плоскости даны две точки и своими координатами относительно некоторой проективной системы координат R

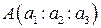
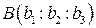
1. На проективной плоскости даны две точки и своими координатами относительно некоторой проективной системы координат R. Написать параметрическое и общее уравнения прямой, проходящей через точки А и В.

Решение.

1) Параметрическое уравнение прямой имеет вид

,

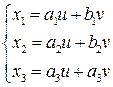
где u, v произвольные действительные числа.

2) Общее уравнение прямой найдем из уравнения

.

Найти координаты точки пересечения прямых, если заданы по две точки на каждой из них.

Решение.

1) Напишем общие уравнения прямых, проходящих через заданные точки. Для этого используем решение предыдущей задачи.

2) Решим систему из двух уравнений, найденных в пункте 1), и найдем координаты 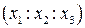их точки пересечения.

Найти двойное отношение четырех точек на проективной прямой

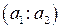
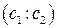
A , B , C , D .

Решение.

По определению двойного отношения

На проективной прямой дано двойное отношение четырех точек и координаты трех из них. Найти координаты четвертой точки, если

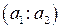
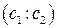
(AB,CD)=k, A , B , C .

Решение.

Обозначим координаты точки D через 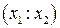. По условию и по определению двойного отношения

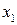
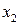
Координаты и не могут одновременно равняться нулю.

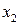
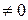
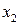
Если, например, , то можно разделить числитель и знаменатель дроби на . Получим

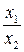
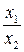
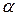
Решив это уравнение относительно , получим численное значение = .

Тогда координаты точки D будут =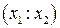

Замечание. Если , то можно делить на и решать аналогично.

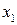
5. На проективной плоскости дано двойное отношение четырех точек и координаты трех из них. Найти координаты четвертой точки, если (AB,CD)= -1, A , B , C . Проверитьколлинеарность точек A, B, C.

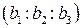
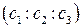
Решение

1) Проверим коллинеарность точек А, В, С.

Точки A , B , C порождаются векторами a , b , c . Точки лежат на одной прямой тогда и только тогда, когда векторы a, b, c линейно зависимы. Чтобы установить это или опровергнуть, проверим равенство или соответственно неравенство нулю определителя

.

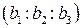
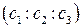
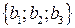
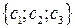
Если определитель равен нулю, то точки коллинеарны. В противном случае неколлинеарны.

2) При условии что точки коллинеарны, найдем координаты четвертой точки D.

Замечание. Эту задачу нельзя решать как предыдущую, так как нам известны не две, а три координаты точек. Для формул же двойного отношения точки должны иметь по две координаты.

Теорема. Пусть на проективной плоскости задана проективная система координат R= и точка М имеет координаты 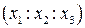относительно R.

Пусть и — проекции точек Е и М из центра на прямую ,

и — проекции точек Е и М из центра на прямую ,

и — проекции точек Е и М из центра на прямую .

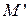
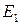
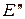
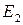
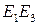
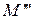
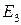
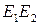
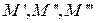
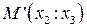
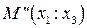
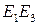
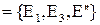
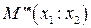
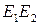
Тогда точки имеют координаты

на прямой относительно R=<E2,E3,E >,

на прямой относительно R ,

на прямой относительно R

Теорема. При центральном проектировании двойное отношение точек не меняется, то есть двойное отношение точек равно двойному отношению их образов.

Рассмотрим проекции точек A, B, C, D на прямую .

, (1)

, (2)

. (3)

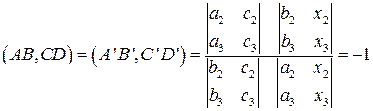
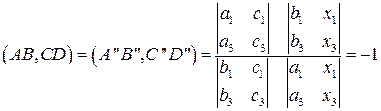
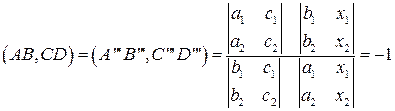
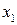
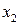
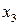
Координаты , , не могут одновременно равняться нулю.

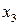
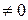
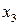
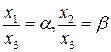
Если, например, , то в равенствах (1) и (2) можно разделить числитель и знаменатель дроби на . Равенство (3) в этом случае нам не понадобится. Из (1) и (2) найдем численные значения .

Получим для координат точки .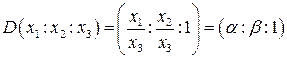

Если , то либо , либо . Выберем ту координату , для которой и повторим для нее рассуждения как для координаты .

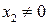
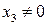
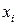
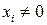
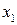
6. На проективной плоскости прямые a, b, c заданы уравнениями

соответственно. Написать уравнение прямой d, если (a b , c d) = -1/3. Проверить принадлежность прямых a, b, c одному пучку.

Решение.

Выпишем координаты прямых

и повторим решение задачи 5, поменяв слова «точка» и «прямая» местами. Мы воспользовались принципом двойственности точек и прямых на проективной плоскости.

Введение (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5

Пусть М – произвольная точка плоскости и пусть эта точка имеет проективные координаты (х1, х2, х3). Проектируем точку Е на прямые А3Y¥, А3X¥ (рис.22).

На расширенной плоскости рассмотрим аффинный репер R = <А3, >.Обозначим аффинные координаты точки М(х, у). Таким образом, репер R¥ = <X¥, Y¥, А3 E> порождает на расширенной аффинной плоскости аффинный репер = <А3, >, где. причем проективные координаты (х1, х2, х3) называют однородными координатами точки М на расширенной плоскости, а (х, у), где , — неоднородными координатами точки М.

На расширенной плоскости задан проективный R = <X¥, Y¥, A3, E> построить точку M (4, -1, 2) по её координатам в репере R.

Две вершины координатного треугольника несобственные:

X¥ Î 2, Y¥ Î 3, È Y¥ = 3. È X¥ =

Строим проекции Е3 и Е2 точки E на прямые 2 и 3.

E3 = (EX¥) Ç 3, E2 = (EY) Ç 2.

Проективный репер R = <X¥, A3, E> порождает аффинный репер = <A3, >, где

Данная точка М будет относительно аффинного репера иметь координаты , .

Подставляя вместо х1, х2, х3 заданные координаты точки М, мы получим, что М имеет аффинные координаты (2, – ).

Построим точку М(2, –) в репере = <A3, > (рис.23). М – искомая точка.

Задачи для самостоятельного решения.

1. На расширенной прямой задан проективный репер R = <A1, A2, E>. Построить точку М(–2, 1) по её координатам в этом репере.

2. На расширенной прямой задан проективный репер R = <A1, M¥, E>. Построить точку М(2, 1) по её координатам в репере R.

3. На расширенной прямой задан проективный репер R = <A1, A2, E>, где Е – середина отрезка A1A2. Найти координаты несобственной точки M¥ прямой относительно репера R.

4. На расширенной прямой заданы точки A1,A2. Построить единичную точку Е проективного репера R = <A1, A2, E>, если известно, что несобственная точка M¥ прямой имеет координаты M¥(–1, 2) в репере R.

5. На расширенной плоскости задан проективный репер R = <A1, A2, A3, E>. Построить точку М(1, 2, 1) по её координатам в репере R.

6. Точка Е – центр тяжести D A1A2A3 на плоскости . Построить точку М(1, 1, –1) по её координатам в проективном репере R = <A1, A2, A3, E> на расширенной плоскости .

7. На расширенной плоскости задан проективный репер R = <A1, A2, M¥, E>. Построить точку М(1, 1, 2) по её координатам в репере R.

§4. Уравнение прямой

Пусть на проективной плоскости выбран проективный репер R = <A1, A2, A3, E>. Прямая d задана точками А(a1, a2, a3) и В(b1, b2, b3). Найдем уравнение прямой d.

Возьмем точку М принадлежащую прямой d. Пусть точка М имеет координаты (х1, х2, х3)относительно проективного репера R. Рассмотрим векторы , , , порождающие точки А, В и М соответственно. Так как точки А, В и М коллинеарны, то есть лежат на одной прямой, то векторы , , линейно зависимы, то есть один из них является линейной комбинацией других: = l + l, где (a1, a2, a3) и (b1, b2, b3). Последнее векторное равенство запишем в координатной форме:

,

, (1)

.

Уравнения (1) называют параметрическими уравнениями прямой d, l и m любые действительные числа, не равные нулю одновременно, называются параметрами.

Так как векторы , , линейно независимы, то

=0 (2)

(2) – уравнение прямой, проходящей через две точки.

Разложим определитель третьего порядка (левой части уравнения (2)) по элементам первой строки, получим:

u1 = , u2 = , u3 = .

Так как rg=2 то миноры второго порядка не равны нулю одновременно .

(u1, u2, u3) называют координатами прямой.

Координаты прямой определяются с точностью до постоянного множителя.

На проективной плоскости задан репер

R = <A1, A2, A3, E>. Еa – проекция точки Е из центра Аa на прямую (АbАg) (a, b, g = ). Найти уравнения координатных прямых (АaАb) и (АaЕa) относительно R.

Так как точки A1, A2 имеют кооординаты A1(1, 0, 0), A2(0, 1, 0), то уравнение прямой (A1A2) имеет вид:

или х3 = 0.

Аналогично получаем уравнения двух других координатных прямых:

Составим уравнение прямой (А1Е1):

Если точка А1 Î (А1Е1), то координаты этой точки удовлетворяют уравнению прямой:

Уравнение прямой примет вид:

Аналогично уравнения прямых:

Доказать, что точки А(а1, а2, а3), В(b1, b2, b3), С(с1, с2, с3) с координатами в проективном репере R = <A1, A2, A3, E> лежат на одной прямой тогда и только тогда, когда

Если точки А, В, С лежат на одной прямой, то векторы, их порождающие: , , линейно независимы, то есть

И обратно, пусть условие (1) выполнено, тогда векторы , , линейно зависимы. Значит, точки p() = А, p() = В, p() = С принадлежат одной прямой.

Найдите координаты точки пересечения прямых 2х1 + х2 + х3 = 0 и 3х1 + 3х2 + 2х3 = 0.

Точка пересечения заданных прямых удовлетворяет системе линейных уравнений:

Из курса алгебры известно, что общее решение этой системы находится по формулам:

x1 = l, x2 = l, x3 = l.

Поэтому для указанной системы x1 = –l, x2 = –l, x3 = 3l. Значит, точка пересечения имеет координаты
(–1, –1, 3).

Какова особенность расположения прямой (AB) относительно репера R = <A1, A2, A3, E> на проективной плоскости, если первые пары координат точек A(a1, a2, a3), B(b1, b2, b3) пропорциональны.

Запишем уравнение прямой (AB):

Разложив по элементам первой строки определитель, получим:

(AB): u1x1 + u2x2 = 0, где u1 = , u1 = .

Уравнению прямой (AB) удовлетворяют координаты A3 (0, 0, 1) вершины репера R. Следовательно, прямая AB проходит через координатную точку A3 проективного репера R.

Построить прямую x1 + 2x2 – 2x3 = 0 по её координатам относительно проективного репера R на расширенной плоскости.

Для построения прямой нужно знать две её точки. Найдём их, положим x1 = 0, x2 = 1. Тогда точка M имеет координаты (0, 1, 1). Аналогично, найдём вторую точку прямой N(2, 0, 1).

Построим точки М и N по их координатам относительно репера R на расширенной плоскости. Видим, что М = Е1 – проекция точки Е из А1. Точка N лежит на прямой А1А3, то есть N = N2. Строим проекцию N2 точки N из центра А2. Точка N2 имеет координаты (2, 1) относительно R2 = <A1, A3, E2>. Искомая прямая проходит через точки Е1 и N2.

Пусть на проективной плоскости заданы две различные прямые а: аaхa = 0 и b: baхa = 0 (a = ) своими уравнениями относительно репера R. Доказать, что уравнение:
(*) lаaхa + mbaхa = 0, где l и m принимают вещественные значения, не равные нулю одновременно, определяет пучок прямых на проективной плоскости.

1. Покажем, что любая прямая пучка, заданного парой пересекающихся прямых а и в, имеет уравнение (*).

2. Уравнение (*) есть уравнение прямой, принадлежащей пучку.

Возьмём любую прямую l пучка на проективной плоскости, заданную уравнением : u1x1 + u2x2 + u3x3 = 0. Так как прямые проходят через одну точку, то:

= 0, то есть

Уравнение прямой l запишется в виде:

Имеем уравнение (*). Покажем, что это уравнение определяет прямую, принадлежащую пучку, определяемому прямыми а и b.

Допустим противное, то есть

А это означает, что координаты прямых а и b пропорциональны. Получили, что прямые а и b совпадают, что противоречит условию задачи.

Значит, уравнение (*) определяет на Р2 прямую l.

Покажем, что точка С =а Ç b принадлежит прямой l, определяемой уравнением (*):

Подставим координаты точки С в уравнение (*):

То есть, уравнение (*) есть уравнение прямой, проходящей через точку С = а Ç b.

Задачи для самостоятельной работы.

1. Найти уравнение прямой на P2 относительно репера R = <A1, A2, A3, E> если она проходит через точки A(2, 3, 2), B(4, –1, 0).

2. Написать параметрические уравнения прямой, проходящей через точки A(1, 1, 2), B(2, 3, 1), имеющие координаты относительно репера R.

3. Найти точку пересечения прямых 2x1 – 3x2 + 5x3 = 0 и x1 + x2 + 3x3 = 0, имеющие данные уравнения относительно репера R.

4. Доказать, что на P2 прямая a(a1, a2, a3) с координатами относительно репера R = <A1, A2, A3, E> проходит через вершину Aa тогда и только тогда, когда aa = 0.

5. Какова особенность расположения точки M пересечения прямых a(a1, a2, a3), b(b1, b2, b3) относительно репера R если первые пары координат этих прямых пропорциональны?

6. Какова особенность прямой l(1, 1, 1) относительно проективного репера R = <A1, A2, A3, E> на расширенной плоскости, если единичная точка репера является точкой пересечения медиан координатного треугольника.

7. Доказать, что прямые a(a1, a2, a3), b(b1, b2, b3), c(c1, c2, c3) с координатами относительно репера R имеют общую точку тогда и только тогда, когда:

= 0.

8. Единичная точка E репера R = <A1, A2, A3, E> на расширенной плоскости является точкой пересечения медиан DA1A2A3. Найти координаты несобственных точек сторон DA1A2A3 и координаты несобственных точек его медиан относительно репера R.

9. Построить прямую a(1, 2, –2) по её координатам относительно заданного на расширенной плоскости проективного репера R = <A1, A2, A3, E>.

10. В пучке прямых на P2, заданном парой прямых
2x1 – 3x2 + 5x3 = 0 и x1 + x2 + 3x3 = 0 относительно репера R = <A1, A2, A3, E>, найти прямую проходящую через точку A(1, 1, 3).

§5. Преобразование проективных координат на проективной прямой и на проективной плоскости

1. Пусть на проективной плоскости R2 задан проективный репер R = <A1, A2, A3, E>. Наряду с проективным репером R возьмем еще один проективный репер R¢ = <A1¢, A2¢, A3¢, E¢>. Причем известно положение нового репера относительно старого, то есть известны координаты новых координатных точек A1¢, A2¢, A3¢ и единичной точки E¢ относительно репера R:

A1¢ = (),

A2¢ = (),

A3¢ = (), (1)

E¢ = ().

Пусть точки A1, A2, A3, E порождаются векторами , , . Причем будем считать, что система векторов <, , , > согласована с репером R, то есть вектор порождает точку A1, вектор – точку А2, вектор – точку А3, а их сумма + + порождает точку Е. В обозначениях, ранее введенных, это выглядит так:p() = A1, p() = A2, p() = A3, p() = Е, = + + .

Обозначим ¢, ¢, ¢, ¢ векторы, порождающие соответственно точки A1¢, A2¢, A3¢, E¢. Их можно разложить по векторам , , следующим образом (см. §3):

,

, (2)

,

.

Пусть М – произвольная точка проективной плоскости и пусть она имеет координаты (х1, х2, х3) в репере R, а в репере R¢ – М(у1, у2, у3). Найдем связь между координатами точки М относительно реперов R, R¢, то есть получим формулы, выражающие старые координаты точки М через её новые координаты.

Возможны 2 случая:

1. Система векторов ¢, ¢, ¢, ¢ согласована относительно репера R¢, то есть вектор ¢, порождающий точку E¢ равен сумме векторов, порождающих точки A1¢, A2¢, A3¢:

¢ = ¢ + ¢ + ¢ (3)

Из (2) и (3) следует, что в этом случае выполняется совокупность равенств (4):

,

, (4)

.

Из того, что точка М имеет координаты (х1, х2, х3) в репере R, следует, что вектор , порождающий точку М (p() = М), имеет координаты <х1, х2, х3> относительно базиса <, , >. Из того, что М(у1, у2, у3)R¢ следует, что вектор , имеющий координаты <у1, у2, у3> относительно базиса <¢, ¢, ¢> также порождает точку М. Тогда по первой аксиоме проективного простраенства = l, l ¹ 0. В последнем равенстве разложим векторы и по векторам соответствующих базисов:

у1¢ + у2¢ + у3¢ = l(х1 + х2 + х3).

Вместо ¢, ¢, ¢ подставим их разложения из формул (2)

у1 + у2 +
+ у3 = l(х1 + х2 + х3). (5)

Так как векторы , , линейно независимы, то, приравнивая коэффициенты при соответствующих векторах в левой и правой частях формулы (5), получим искомые формулы преобразования координат:

lх1 = у1 + у2 + у3,

lх2 = у1 + у2 + у3, (6)