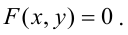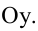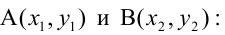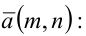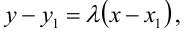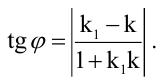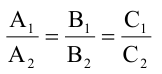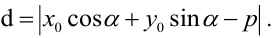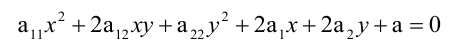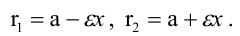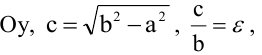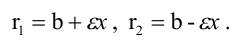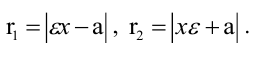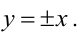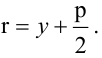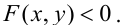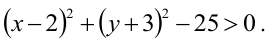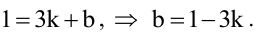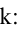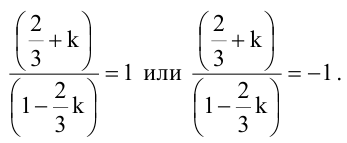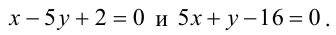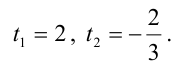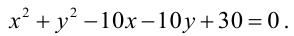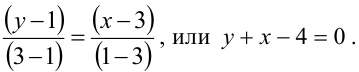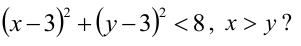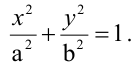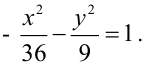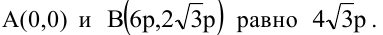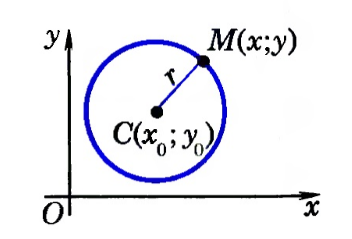Уравнения прямых и кривых на плоскости с примерами решения
Содержание:
Уравнения прямых и кривых на плоскости
Уравнения кривых в большом количестве встречаются при чтении экономической литературы. Укажем некоторые из этих кривых.
Кривая безразличия — кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.
Кривая потребительского бюджета — кривая, показывающая различные комбинации количеств двух товаров, которые потребитель может купить при данном уровне его денежного дохода.
Кривая производственных возможностей — кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объема производства в экономике с постоянными запасами ресурсов и неизменной технологией.
Кривая инвестиционного спроса — кривая, показывающая динамику процентной ставки и объем инвестиций при разных процентных ставках.
Кривая Филлипса — кривая, показывающая существование устойчивой связи между уровнем безработицы и уровнем инфляции.
Кривая Лаффера — кривая, показывающая связь между ставками налогов и налоговыми поступлениями, выявляющая такую налоговую ставку, при которой налоговые поступления достигают максимума.
Уже простое перечисление терминов показывает, как важно для экономистов умение строить графики и анализировать уравнения кривых, каковыми являются прямые линии и кривые второго порядка — окружность, эллипс, гипербола, парабола. Кроме того, при решении большого класса задач требуется выделить на плоскости область, ограниченную какими-либо кривыми, уравнения которых заданы. Чаще всего эти задачи формулируются так: найти наилучший план производства при заданных ресурсах. Задание ресурсов имеет обычно вид неравенств, уравнения которых даны. Поэтому приходится искать наибольшее или наименьшее значения, принимаемые некоторой функцией в области, заданной уравнениями системы неравенств.
В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению
Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:
1. Общее уравнение прямой:
Вектор 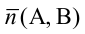
2. Уравнение прямой с угловым коэффициентом:
где 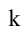
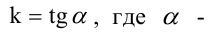
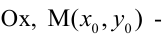
Уравнение (2.2) принимает вид 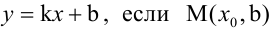
3. Уравнение прямой в отрезках:
где а и b — величины отрезков, отсекаемых прямой на осях координат.
4. Уравнение прямой, проходящей через две данные точки —
5. Уравнение прямой, проходящей через данную точку 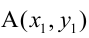
6. Нормальное уравнение прямой:
где 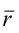
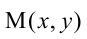
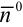
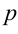
Нормальное уравнение прямой в координатной форме имеет вид:
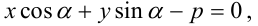
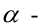
Уравнение пучка прямых с центром в точке 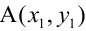
где 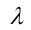
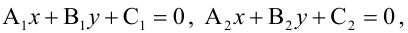
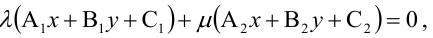
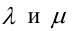
Величина угла между прямыми 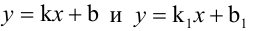
Равенство 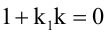
Для того, чтобы два уравнения

Уравнения (2.7), (2.8) задают две различные параллельные прямые, если 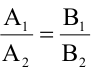
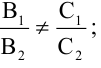
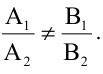
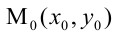
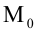
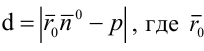
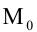
Общее уравнение кривой второго порядка имеет вид:
Предполагается, что среди коэффициентов уравнения 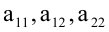
Уравнение окружности с центром в точке 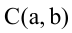

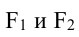
Эллипс, заданный уравнением (2.10), симметричен относительно осей координат.
Параметры а и b называются полуосями эллипса.
Пусть 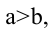
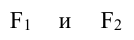
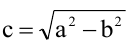
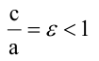
Расстояния от точки 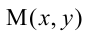
Если же 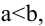
Если а=b, то эллипс является окружностью с центром в начале координат радиуса а.
Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек 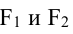
Каноническое уравнение гиперболы:
Гипербола, заданная уравнением (2.11), симметрична относительно осей координат. Она пересекает ось 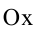
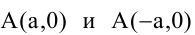
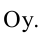
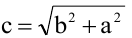
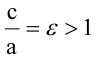
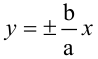
Расстояния от точки 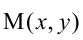
Гипербола, у которой а=b, называется равносторонней, ее уравнение 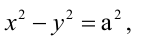
Гиперболы 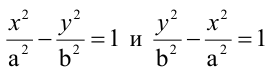
Каноническое уравнение параболы имеет два вида:
1. 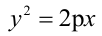
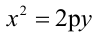
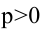
Парабола, уравнение которой 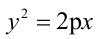
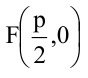
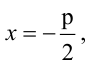
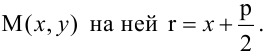
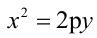
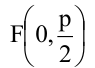
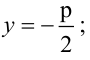
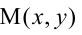
Уравнение 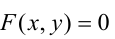
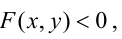
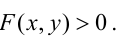
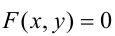
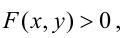
Прямая, уравнение которой 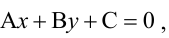
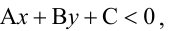
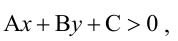
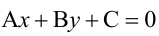
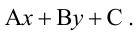
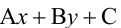
Точно так же решаются и нелинейные неравенства с двумя неизвестными.
Например, решим неравенство 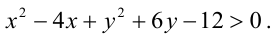
Уравнение 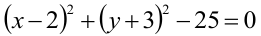
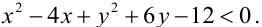
Пример:
Составьте уравнения прямых, проходящих через точку А(3,1) и наклоненных к прямой 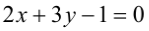
Решение:
Будем искать уравнение прямой в виде 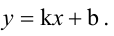
Величина угла между прямыми 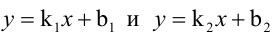
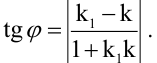
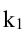
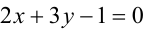
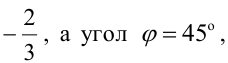
Имеем два значения 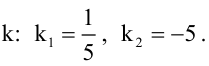
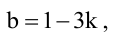
Пример:
При каком значении параметра t прямые, уравнения которых 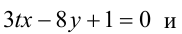
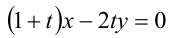
Решение:
Прямые, заданные общими уравнениями, параллельны, если коэффициенты при x и y пропорциональны, т.е. 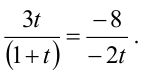
Пример:
Найти уравнение общей хорды двух окружностей: 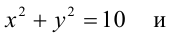
Решение:
Найдем точки пересечения окружностей, для этого решим систему уравнений: 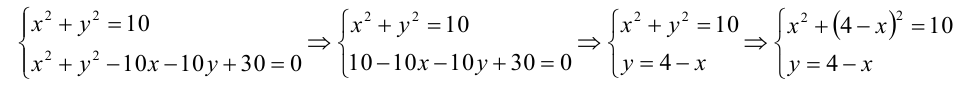
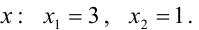
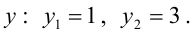
Пример:
Как расположены на плоскости точки, координаты которых удовлетворяют условиям
Решение:
Первое неравенство системы определяет внутренность круга, не включая границу, т.е. окружность с центром в точке (3,3) и радиуса 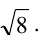
Пример:
Вычислить длину стороны квадрата, вписанного в эллипс, уравнение которого
Решение:
Пусть 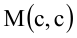
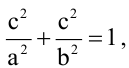
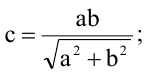
Пример:
Зная уравнение асимптот гиперболы 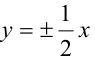
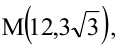
Решение:
Запишем каноническое уравнение гиперболы: 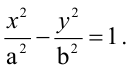
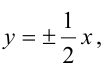
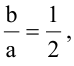
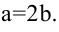
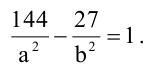
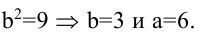
Пример:
Вычислить длину стороны правильного треугольника АВС, вписанного в параболу с параметром р, предполагая, что точка А совпадает с вершиной параболы.
Решение:
Каноническое уравнение параболы с параметром р имеет вид 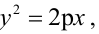
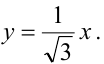
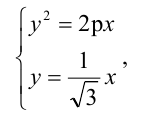
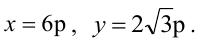
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоскость и прямая в пространстве
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Производные тригонометрических функции
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Уравнение окружности и прямой
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
ТЕМА: «Уравнение окружности и прямой» Цели урока: Повторить уравнение окружности и прямой. Показать применение уравнений окружности и прямой при решении задач. Совершенствование навыков решения задач методом координат.
1. Как называется геометрическая фигура, состоящая из множества всех точек, равноудаленных от данной точки? Математический диктант Проверить 1. Окружность
2. Как называется хорда, проходящая через центр окружности? Проверить 2. Диаметр
3. Как называется отрезок, соединяющий центр окружности с точкой на окружности? Проверить 3. Радиус
4. Как называется геометрическая фигура, состоящая из множества всех точек плоскости, находящихся от данной точки на расстоянии, не превышающем данного? Проверить 4. Круг
5. Пересекаются ли окружности с центрами А и В, если АВ = 10 см, а радиусы равны 5 см, и 6 см? Проверить 5. Пересекаются
6. Расстояние от центра окружности до точки А равно d, а радиус окружности равен r. Сравните d и r, если точка А лежит вне круга, ограниченного данной окружностью? Проверить 6. d > r
7. Расстояние от центра окружности до точки В равно m, а радиус окружности равен r. Сравните m и r, если точка B лежит внутри круга, ограниченного данной окружностью? Проверить 7. m (0 – 1)2 + (0 + 3)2 = 9 > (0 – 1)2 + (1 + 3)2 = 9 > x
Дана окружность Определите, какие из точек А(-4; 3), В(5; 1), С(-5; 4), D(10; 5) лежат: а) на окружности; б) внутри круга, ограниченного данной окружностью; в) вне круга, ограниченного данной окружностью. (x – 4 )2 + (y + 3)2 = 100 (– 4 – 4)2 + (3 + 3)2 > 100 (5 – 4)2 + (1 + 3)2 100 (10 – 4)2 + (5 + 3)2 = 100
Найдите множество точек, удаленных от окружности на расстояние 3. x 2 + y 2 = 16 x y x 2 + y 2 = 49 x 2 + y 2 = 1
(x + 5)2 + (y – 5)2 = 25 Центр? Радиус? O1(-5;5) r = 5 x y A O O1 450 5 5
Центр? Радиус? x y O1 O E 300 На чертеже расстояние ОО1= , ОЕ – касательная к окружности. EOF = 600. Написать уравнение окружности. ОЕ = ОF, отрезки касательных 6
Домашнее задание п. 93 — 95 № 972(б), 973, 978 (а)
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 949 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 681 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 314 человек из 70 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 568 866 материалов в базе
Материал подходит для УМК
«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
§ 3. Уравнения окружности и прямой
Другие материалы
- 09.11.2020
- 466
- 17
- 30.09.2020
- 356
- 11
- 09.01.2020
- 3719
- 195
- 21.12.2019
- 1392
- 45
- 30.11.2019
- 1201
- 47
- 31.10.2019
- 760
- 44
- 30.10.2019
- 2062
- 197
- 16.08.2019
- 798
- 8
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 07.12.2020 1055
- PPTX 3 мбайт
- 50 скачиваний
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Малышок Елена Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 8 лет и 2 месяца
- Подписчики: 1
- Всего просмотров: 33925
- Всего материалов: 28
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Забайкалье в 2022 году обеспечат интернетом 83 школы
Время чтения: 1 минута
У 76% российских учителей оклад ниже МРОТ
Время чтения: 2 минуты
Профессия педагога на третьем месте по популярности среди абитуриентов
Время чтения: 1 минута
Рособрнадзор не планирует переносить досрочный период ЕГЭ
Время чтения: 0 минут
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
В Воронеже продлили удаленное обучение для учеников 5-11-х классов
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Уравнение окружности и прямой
Вы будете перенаправлены на Автор24
Уравнение линии на плоскости
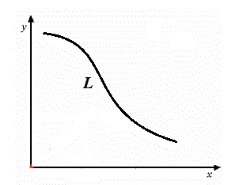
Введем для начала понятие уравнения линии в двумерной системе координат. Пусть в декартовой системе координат построена произвольная линия $L$ (Рис. 1).
Рисунок 1. Произвольная линия в системе координат
Уравнение с двумя переменными $x$ и $y$ называется уравнением линии $L$, если этому уравнению удовлетворяют координаты любой точки, принадлежащей линии $L$ и не удовлетворяет ни одна точка, не принадлежащая линии $L.$
Уравнение окружности
Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).
Рисунок 2. Окружность в декартовой системе координат
Расстояние от центра окружности до точки $M$ вычисляется следующим образом
Но, так как $M$ лежит на окружности, то получаем $CM=r$. Тогда получим следующее
Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.
В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид
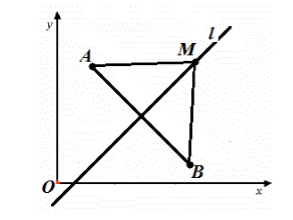
Выведем уравнение прямой $l$ в декартовой системе координат $xOy$. Пусть точки $A$ и $B$ имеют координаты $\left\
Готовые работы на аналогичную тему
Рисунок 3. Прямая в декартовой системе координат
Так как прямая $l$ — серединный перпендикуляр к отрезку $AB$, то точка $M$ равноудалена от концов этого отрезка, то есть $AM=BM$.
Найдем длины данных сторон по формуле расстояния между точками:
Обозначим через $a=2\left(x_1-x_2\right),\ b=2\left(y_1-y_2\right),\ c=
Здесь можно выделить два частных случая для уравнения прямой. Пусть прямая $l$ проходит через точку $M=\
Если прямая $l$ параллельна оси $Ox$, то она имеет вид
Если прямая $l$ параллельна оси $Oy$, то она имеет вид
Пример задачи на нахождение уравнений линий в декартовой системе координат
Найти уравнение окружности с центром в точке $(2,\ 4)$. Проходящей через начало координат и прямую, параллельную оси $Ox,$ проходящей через её центр.
Решение.
Найдем сначала уравнение данной окружности. Для этого будем использовать общее уравнение окружности (выведенное выше). Так как центр окружности лежит в точке $(2,\ 4)$, получим
Найдем радиус окружности как расстояние от точки $(2,\ 4)$ до точки $(0,0)$
Получаем, уравнение окружности имеет вид:
Найдем теперь уравнение окружности, используя частный случай 1. Получим
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 05 04 2021
http://infourok.ru/uravnenie-okruzhnosti-i-pryamoj-4642598.html
http://spravochnick.ru/matematika/metod_koordinat/uravnenie_okruzhnosti_i_pryamoy/