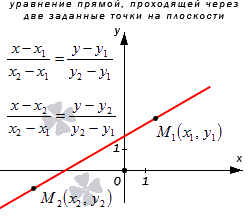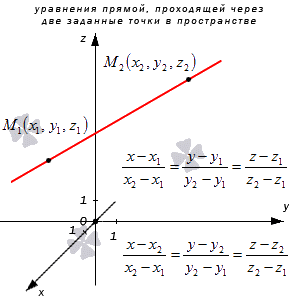Уравнение прямой по двум точкам геометрия 9 класс

Уравнение прямой, которая проходит через две заданные точки: примеры, решения

Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.

Уравнение прямой, проходящей через две заданные точки на плоскости

Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.

Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.

Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a , проходящей через две несовпадающие точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , находящиеся в декартовой системе координат.

В каноническом уравнении прямой на плоскости, имеющего вид x — x 1 a x = y — y 1 a y , задается прямоугольная система координат О х у с прямой, которая пересекается с ней в точке с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) .

Необходимо составить каноническое уравнение прямой a , которая пройдет через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) .

Прямая а имеет направляющий вектор M 1 M 2 → с координатами ( x 2 — x 1 , y 2 — y 1 ) , так как пересекает точки М 1 и М 2 . Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 ) и координатами лежащих на них точках M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 .

Рассмотрим рисунок, приведенный ниже.

Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ .

Рассмотрим подробней на решении нескольких примеров.

Записать уравнение прямой, проходящей через 2 заданные точки с координатами M 1 — 5 , 2 3 , M 2 1 , — 1 6 .

Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x 1 , y 1 и x 2 , y 2 принимает вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . По условию задачи имеем, что x 1 = — 5 , y 1 = 2 3 , x 2 = 1 , y 2 = — 1 6 . Необходимо подставить числовые значения в уравнение x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 . Отсюда получим, что каноническое уравнение примет вид x — ( — 5 ) 1 — ( — 5 ) = y — 2 3 — 1 6 — 2 3 ⇔ x + 5 6 = y — 2 3 — 5 6 .

Ответ: x + 5 6 = y — 2 3 — 5 6 .

При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.

Составить общее уравнение прямой, проходящей через точки с координатами M 1 ( 1 , 1 ) и M 2 ( 4 , 2 ) в системе координат О х у .

Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида x — 1 4 — 1 = y — 1 2 — 1 ⇔ x — 1 3 = y — 1 1 .

Приведем каноническое уравнение к искомому виду, тогда получим:

x — 1 3 = y — 1 1 ⇔ 1 · x — 1 = 3 · y — 1 ⇔ x — 3 y + 2 = 0

Ответ: x — 3 y + 2 = 0 .

Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y = k x + b . Если необходимо найти значение углового коэффициента k и числа b , при которых уравнение y = k x + b определяет линию в системе О х у , которая проходит через точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , где x 1 ≠ x 2 . Когда x 1 = x 2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М 1 М 2 определена общим неполным уравнением вида x — x 1 = 0 .

Потому как точки М 1 и М 2 находятся на прямой, тогда их координаты удовлетворяют уравнению y 1 = k x 1 + b и y 2 = k x 2 + b . Следует решить систему уравнений y 1 = k x 1 + b y 2 = k x 2 + b относительно k и b .

Для этого найдем k = y 2 — y 1 x 2 — x 1 b = y 1 — y 2 — y 1 x 2 — x 1 · x 1 или k = y 2 — y 1 x 2 — x 1 b = y 2 — y 2 — y 1 x 2 — x 1 · x 2 .

С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 1 или y = y 2 — y 1 x 2 — x 1 · x + y 2 — y 2 — y 1 x 2 — x 1 · x 2 .

Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.

Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M 2 ( 2 , 1 ) и y = k x + b .

Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y = k x + b . Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M 1 ( — 7 , — 5 ) и M 2 ( 2 , 1 ) .

Точки М 1 и М 2 располагаются на прямой, тогда их координаты должны обращать уравнение y = k x + b верное равенство. Отсюда получаем, что — 5 = k · ( — 7 ) + b и 1 = k · 2 + b . Объединим уравнение в систему — 5 = k · — 7 + b 1 = k · 2 + b и решим.

При подстановке получаем, что

— 5 = k · — 7 + b 1 = k · 2 + b ⇔ b = — 5 + 7 k 2 k + b = 1 ⇔ b = — 5 + 7 k 2 k — 5 + 7 k = 1 ⇔ ⇔ b = — 5 + 7 k k = 2 3 ⇔ b = — 5 + 7 · 2 3 k = 2 3 ⇔ b = — 1 3 k = 2 3

Теперь значения k = 2 3 и b = — 1 3 подвергаются подстановке в уравнение y = k x + b . Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y = 2 3 x — 1 3 .

Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.

Запишем каноническое уравнение прямой, проходящей через M 2 ( 2 , 1 ) и M 1 ( — 7 , — 5 ) , имеющее вид x — ( — 7 ) 2 — ( — 7 ) = y — ( — 5 ) 1 — ( — 5 ) ⇔ x + 7 9 = y + 5 6 .

Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x + 7 9 = y + 5 6 ⇔ 6 · ( x + 7 ) = 9 · ( y + 5 ) ⇔ y = 2 3 x — 1 3 .

Ответ: y = 2 3 x — 1 3 .

Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве

Если в трехмерном пространстве имеется прямоугольная система координат О х у z с двумя заданными несовпадающими точками с координатами M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , проходящая через них прямая M 1 M 2 , необходимо получить уравнение этой прямой.

Имеем, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z и параметрические вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ способны задать линию в системе координат О х у z , проходящую через точки, имеющие координаты ( x 1 , y 1 , z 1 ) с направляющим вектором a → = ( a x , a y , a z ) .

Прямая M 1 M 2 имеет направляющий вектор вида M 1 M 2 → = ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) , где прямая проходит через точку M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , отсюда каноническое уравнение может быть вида x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 или x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , в свою очередь параметрические x = x 1 + ( x 2 — x 1 ) · λ y = y 1 + ( y 2 — y 1 ) · λ z = z 1 + ( z 2 — z 1 ) · λ или x = x 2 + ( x 2 — x 1 ) · λ y = y 2 + ( y 2 — y 1 ) · λ z = z 2 + ( z 2 — z 1 ) · λ .

Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.

Написать уравнение прямой, определенной в прямоугольной системе координат О х у z трехмерного пространства, проходящей через заданные две точки с координатами M 1 ( 2 , — 3 , 0 ) и M 2 ( 1 , — 3 , — 5 ) .

Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 .

По условию имеем, что x 1 = 2 , y 1 = — 3 , z 1 = 0 , x 2 = 1 , y 2 = — 3 , z 2 = — 5 . Отсюда следует, что необходимые уравнения запишутся таким образом:

x — 2 1 — 2 = y — ( — 3 ) — 3 — ( — 3 ) = z — 0 — 5 — 0 ⇔ x — 2 — 1 = y + 3 0 = z — 5

Ответ: x — 2 — 1 = y + 3 0 = z — 5 .

Разработка урока по геометрии «Уравнение прямой»(9 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Конспект урока Уравнение прямой.docx

Муниципальное автономное общеобразовательное учреждение

средняя общеобразовательная школа № 45

Разработка урока по теме

геометрия, 9 класс.

Автор: учитель математики

МАОУ СОШ №45 г. Калининграда

Борисова Алла Николаевна.

2017 – 2018 учебный год

Автор – Борисова Алла Николаевна

Образовательное учреждение – муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа № 45 города Калининграда

Предмет – математика (геометрия)

Тема – «Уравнение прямой»

Геометрия, 7 — 9: учебник для общеобразовательных учреждений/ Л. С. Атанасян и др., — 17 — е изд., — М.: Просвещение, 2016 г.

Рабочая тетрадь «Геометрия, 8 класс», авторы Л. С. Атанасян, В. Ф. Бутузов, Ю.А. Глазков, И.И. Юдина/ учебное пособие для учащихся общеобразовательных учреждений/ — М. Просвещение, 2016 г.

Данные о программах, в которых выполнена мультимедийная составляющая работы — Microsoft Office Power Point 2010

Цель: вывести уравнение прямой и показать применение уравнения прямой при решении задач.

вывести уравнение прямой;

научить пользоваться новыми знаниями при составлении и построении прямой.

развить умения и навыки при составлении уравнения прямой;

развитие познавательного интереса к предмету;

продемонстрировать учащимся межпредметные связи, возможность применения полученных знаний в других предметных областях;

развивать образное и логическое мышление;

развивать коммуникативные компетенции.

в оспита ть настойчивости в достижении цели .

воспитание познавательной активности, культуры общения, ответственности, самостоятельное развитие зрительной памяти;

п ривит ь учащимся навыков самостоятельной работы ;

оптимизировать обучение путем разумного сочетания и соотношения методов, средств и форм, направленных на получение высокого результата за время урока.

Оборудование и материалы для урока : проектор, экран, презентация для сопровождения урока.

Тип урока: урок изучения нового материала.

1) Учащимся сообщается тема урока и цели, подчеркивается актуальность данной темы (слайд №1).

2) Объявляется план урока.

1. Проверка домашнего задания.

3. Открытие нового знания.

II . Проверка домашнего задания.

Проверить наличие выполненных домашних заданий и ответить на вопросы, которые возникли у учеников во время их выполнения.

I V. Введение нового материала.

1. Вывести уравнение прямой в заданной прямоугольной системе координат: ах+ву+с=0

Вывод: у равнением любой прямой в прямоугольной системе координат является уравнение первой степени с двумя переменными (слайд №4) .

2.Рассмотреть частные случаи уравнения прямой, проходящей через точку

а) уравнение горизонтальной прямой, параллельной оси Ох ,

б) уравнение вертикальной прямой, параллельной оси Оу ,

и рассмотреть примеры.

V . Закрепление изученного материала.

1) Первичное закрепление.

Разобрать решение задачи (слайды № 10 — 11) .

Напишите уравнение прямой, которая проходит через точки Р(2; 1), Q (−3;−1).

2) Самостоятельное решение задач.

Работают самостоятельно (по необходимости пользуются помощью учителя или соседа по парте). Двое учащихся работают на откидной доске. После окончания работы взаимопроверка .

№ 26, 27 (из рабочей тетради) .

Работают самостоятельно в тетради. При необходимости учитель даёт консультации. Затем решения оформляются на доске.

№ 972(б), 973, дополнительная задача.

Точки С(2;5) и D(5;2) лежат на прямой, значит их координаты удовлетворяют уравнению прямой ах+ву+с=0. Отсюда

Выразим коэффициенты и через и подставим их в уравнение ах+ву+с=0.

Значит, /: с, с ≠ 0, получаем

Так как СМ — медиана треугольника АВС , то М — середина отрезка АВ , т. е.

Напишем уравнение прямой, проходящей через точки и М(0;3). Подставим коэффициенты точек С и М в уравнение ах+ву+с=0.

Получим уравнение прямой СМ .

Параллелограмм ABCD задан координатами трёх своих вершин: A(- 1;1), B(1;7), D(7;-3). Напишите уравнение прямых ВС и DC . Вычислите площадь данного треугольника.

VI . Подведение итогов урока.

Подведем итоги урока.

С чем мы сегодня познакомились на уроке?

Назовите общий вид уравнения прямой.

Какое уравнение имеет прямая параллельная Ох, Оу ?

Выставление отметок за урок.

П. 92, №972(в), 974, 976, 977.

Выбранный для просмотра документ Уравнение прямой.pptx

Описание презентации по отдельным слайдам:

«Уравнение прямой» Геометрия 9 класс.

Устная работа 1. Напишите уравнение окружности с центром в точке С(3;0), с радиусом равным 2. (х – 3)2 + у 2 = 4 Принадлежит ли точка Е(3;7) линии, заданной уравнением х2 − 4х + у =4? Докажите, что АВ – хорда окружности (х – 4)2 + (у − 1)2 = 25, если А(0; −2), В(4;6). Да

Устная работа Найдите координаты центра окружности с диаметром CD, если С(4; −7), D(2; −3). (3;5) Функция задана уравнением . Какая линия служит графиком данной функции? Проходит ли прямая, заданная уравнением у = 3х + 2, через IV координатную плоскость? Нет, k >0 Прямая

Итак , уравнение прямой: где a, b и c – некоторые числа

Все точки прямой имеют одну и ту же ординату у0. Значит, координаты любой точки прямой l удовлетворяют уравнению: у = у0 Это значит, что уравнение задает на плоскости горизонтальную прямую. а)уравнение горизонтальных прямых М0 (х0; у0) l l║Oх М0 (х0; у0)ϵ l у0 у = у0

Примеры y = 4 y = -2 y = 0 у = 0 – уравнение оси Ох

б) уравнение вертикальных прямых n║Oу М0 (х0; у0)ϵ n l n М0 (х0; у0) у0 x0 Все точки прямой имеют одну и ту же абсциссу х0. Значит, координаты любой точки прямой n удовлетворяют уравнению: х = х0 Это значит, что уравнение задает на плоскости вертикальную прямую. х = х0

x = 3 x = -2 x = 0 Примеры х = 0 – уравнение оси Оу

Задача Напишите уравнение прямой, которая проходит через точки Р(2; 1), Q(−3;−1). Решение a ∙ 2+ b ∙ 1+ c = 0, a ∙ (−3)+ b ∙ (−1) + c = 0; 2a + b + c = 0, (1) −3а − b + c = 0; (2) Прямая имеет уравнение вида ax + by + c = 0. Подставляя координаты Р и Q в это уравнение, получим:

1) Выразим коэффициенты a и b через коэффициент c: (1) 2a + b + c = 0, b = −2а −с 2)Подставим найденное значение b в уравнение (2): −3а − b + c = 0; −3а − (−2а −с) + c = 0; −3а + 2а + с + c = 0; −а + 2с = 0; −а = − 2с; а = 2с; 3) Найдём b : b = −2∙ 2с −с b = − 5с 2)Подставим найденные значение а и b в уравнение прямой: 2с ∙ x − 5с ∙ y + c = 0 с(2 x − 5y + 1) = 0 / : с ≠ 0 2 x − 5y + 1 = 0 Получаем уравнение искомой прямой:

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 929 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 686 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 313 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 586 655 материалов в базе

Материал подходит для УМК

«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

92. Уравнение прямой

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 19.11.2017
• 2320
• 14

• 19.11.2017
• 2752
• 14

• 18.11.2017
• 673
• 1

• 18.11.2017
• 788
• 3

• 18.11.2017
• 985
• 2

• 18.11.2017
• 389
• 0

• 18.11.2017
• 2190
• 40

• 18.11.2017
• 441
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 19.11.2017 11744
• RAR 3.9 мбайт
• 778 скачиваний
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Борисова Алла Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 5 месяцев
• Подписчики: 6
• Всего просмотров: 293569
• Всего материалов: 111

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В школах Хабаровского края введут уроки спортивной борьбы

Время чтения: 1 минута

Ленобласть распределит в школы прибывающих из Донбасса детей

Время чтения: 1 минута

В Ленобласти школьники 5-11-х классов вернутся к очному обучению с 21 февраля

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

РДШ организовало сбор гуманитарной помощи для детей из ДНР

Время чтения: 1 минута

В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Получите новую специальность с дополнительной скидкой 10%

Цена от 4900 740 руб. Промокод (до 23 февраля): Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки

Уравнение прямой проходящей через две точки

Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.

Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнения прямой, проходящей через две точки могут быть следующих видов:

• каноническое уравнение,
• параметрическое уравнение,
• общее уравнение прямой,
• уравнение прямой с угловым коэффициентом,
• уравнение прямой в полярных координатах и другие.

Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.