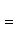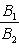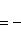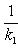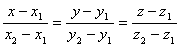Уравнение прямой проходящее через перпендикулярный вектор

Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

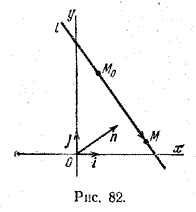
Пусть дана некоторая точка М₀ и вектор n. Проведем через точку М₀ прямую l перпендикулярно вектору n (рис. 82).

Пусть M — произвольная точка. Точка M лежит на прямой l в том и только в том случае, когда вектор \(\overrightarrowM>\) перпендикулярен вектору n, а для этого необходимо и достаточно, чтобы скалярное произведение векторов n и \(\overrightarrowM>\) равнялось нулю:

Чтобы выразить последнее равенство в координатах, введем прямоугольную декартову систему координат. Пусть точки M₀ и M имеют координаты (x₀ ; у₀ ) и (x; у).

Тогда \(\overrightarrowM>\) = (x — x₀; у — у₀). Обозначим координаты нормального вектора n через (А; В). Теперь равенство (1) можно записать так:

Уравнение (2) есть уравнение прямой l, проходящей через данную точку М₀ (x₀; у₀) перпендикулярно данному вектору n = (А; В).

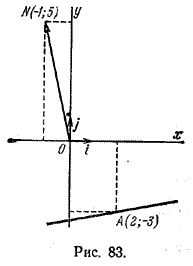
Задача 1. Составить уравнение прямой, проходящей через точку А (2; -3) перпендикулярно вектору n = (-1;5) (рис.83).

Пользуясь формулой (2), находим уравнение данной прямой:

— 1 • (x-2) + 5 • (у + 3) = 0

или, окончательно, x — 5у — 17 = 0.

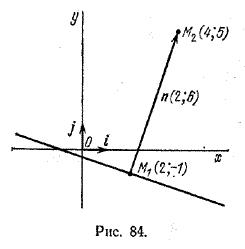
Задача 2. Даны точки M₁(2; -1) и M₂(4; 5). Написать уравнение прямой, проходящей через точку М₁ перпендикулярно вектору \(\overrightarrowM_<2>>\).

Нормальный вектор искомой прямой n = \(\overrightarrowM_<2>>\) имеет координаты (2; 6) (рис. 84).

Следовательно, по формуле (2) получим уравнение

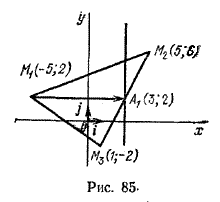
Задача 3. В треугольнике с вершинами в точках M₁(-5; 2), M₂(5; 6) и M₃(1; -2) проведена медиана M₁А₁. Требуется составить уравнение прямой, проходящей через точку А₁ перпендикулярно медиане M₁A₁ (рис. 85).

За нормальный вектор искомой прямой можно принять вектор n = \(\overrightarrowA_<1>>\). Определим его координаты. Точка A₁ — середина отрезка M₂M₃, поэтому, если (x₁; y₁) — ее координаты, то \( x_1 = \frac<5+1><2>=3, \;\;а \;\; y_1=\frac<6-2><2>=2 \).

Тогда нормальный вектор n = \(\overrightarrowA_<1>>\) имеет координаты (8; 0). Следовательно, искомое уравнение прямой имеет вид

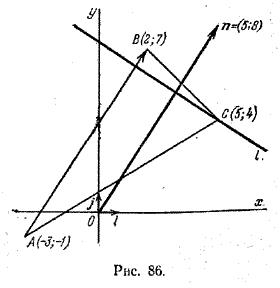
Задача 4. Дан треугольник с вершинами в точках А(-3; -1), В(2; 7) и С(5; 4). Требуется составить уравнение прямой, проходящей через вершину С перпендикулярно стороне AB (рис. 86).

За нормальный вектор искомой прямой можно взять вектор n = \(\overrightarrow\).

Так как n = (2-(-3); 7 — (-1)) = (5; 8), то, подставляя координаты точки С и координаты вектора n в формулу (2), получим

или, окончательно, 5х + 8у — 57 = 0.

Уравнение перпендикулярной прямой

Альтернативная формула
Прямая, проходящая через точку M₁(x₁; y₁) и перпендикулярная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения перпендикулярной прямой (см. также как составить уравнение параллельной прямой).

Пример №1 . Составить уравнение прямой, проходящей через точку (2; -1) и перпендикулярной 4x-9y=3 .
Решение. Данную прямую можно представить уравнением y = 4 /₉x – 1 /₃ (a = 4 /₉). Уравнение искомой прямой есть y+1 = -9/4(x-2) , т.е. 9x+4y-14=0 .

Пример №2 . Решая пример 1 (A=4, B=-9) по формуле (2), найдем 4(y+1)+9(x-2)=0 , т.е. 9x+4y-14=0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-3, -2) перпендикулярно прямой 2y+1=0 .
Решение. Здесь A=0, B=2. Формула (2) дает -2(x+3)=0, т.е. x+3=0 . Формула (1) неприменима, так как a=0 .

Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

Найдем уравнение прямой, проходящей через заданную точку М0(х0,у0) перпендикулярно данному ненулевому вектору .

Возьмем на прямой произвольную точку М(х;у) и рассмотрим вектор .Поскольку векторы n и М0М перпендикулярны, то их скалярное произведение равно нулю: ,то есть Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.

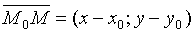
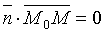
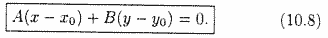
Общее уравнение прямой на плоскости.

Любая прямая на плоскости может быть задана уравнением первого порядка

Угол между прямыми. Условия параллельности и перпендикулярности прямых.

Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.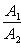

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.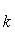

б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства A1A2 + B1B2 = 0.

Вычисление расстояния от точки до прямой.

Расстояние от точки до прямой определяется длиной перпендикуляра, опущенного из точки на прямую.

Уравнение плоскости, проходящей через три точки.

| x — x1 y — y1 z — z1 |

| x2 — x1 y2 — y1 z2 — z1 | = 0

| x3 — x1 y3 — y1 z3 — z1 |

Уравнение плоскости проходящей через данную точку перпендикулярно данному вектору.

Пусть в трехмерном пространстве задана прямоугольная декартова система координат. Сформулируем следующую задачу:

Составить уравнение плоскости, проходящей через данную точку

M(x0, y0, z0) перпендикулярно данному вектору →n = .

Решение. Пусть P(x, y, z) — произвольная точка пространства. Точка P принадлежит плоскости тогда и только тогда, когда вектор

MP = ортогонален вектору →n = (рис.1).

Написав условие ортогональности этих векторов (→n, MP) = 0 в координатной форме, получим:

A(x − x0) + B(y − y0) + C(z − z0) = 0 (1)

Это и есть искомое уравнение. Вектор →n = называется нормальным вектором плоскости.

Таким образом, чтобы написать уравнение плоскости, нужно знать нормальный вектор плоскости и какую–нибудь точку, принаждежащую плоскости.

Если теперь в уравнении (1) раскрыть скобки и привести подобные члены, получим общее уравнение плоскости:

Ax + By + Cz + D = 0 ,

где D = −Ax0 − By0 − Cz0 .

Уравнение прямой, проходящей через две точки в пространстве.

Уравнение прямой, проходящей через данную точку параллельно данному вектору(в пространстве).

Уравнение прямой, проходящей через данную точку A(x1, y1) параллельно данному вектору a(m, n):

Условия параллельности и перпендикулярности прямой и плоскости.

Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.

Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.

Вычисление расстояния от данной точки до данной плоскости.

Пусть Pa = (xa, ya, za) точка, расстояние от которой необходимо подсчитать.

Плоскость можно задать нормалью n = (A, B, C) и одной точкой Pb = (xb, yb, zb)

Произвольная точка P = (x,y,z) лежит на плоскости тогда и только тогда, когда Ax+By+Cz+D=0

Наименьшее расстояние между Pa и плоскостью будет равно абсолютной величине выражения (A xa + B ya + C za + D) / sqrt(A2 + B2 + C2)

Знак самого выражения дает расположение точки относительно плоскости: с какой она стороны.

Уравнение окружности.

или .

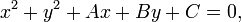
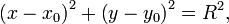
Эллипс.

Эллипсом называется множество всех таких точек плоскости, для которых сумма расстояний до двух фиксированных точек постоянна.

Гипербола.

Гиперболой называется множество всех таких точек плоскости, для которых модуль разности расстояний до двух фиксированных точек есть постоянная положительная величина.

Парабола.

Параболой называется множество всех таких точек плоскости, для которых расстояние до фиксированной точки равно расстоянию до фиксированной прямой, не проходящей через эту точку.