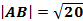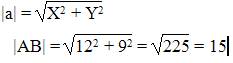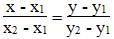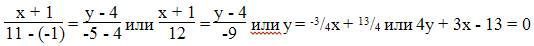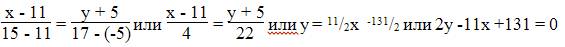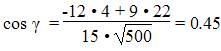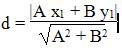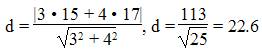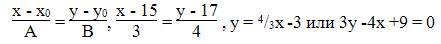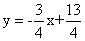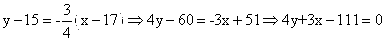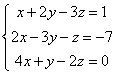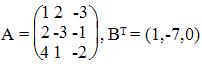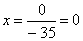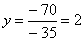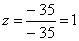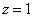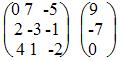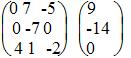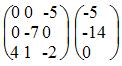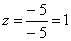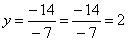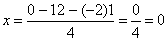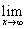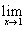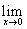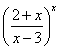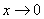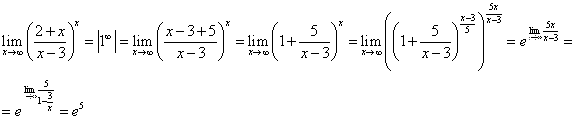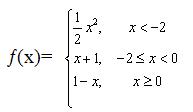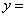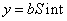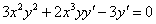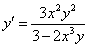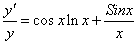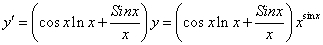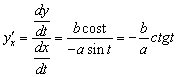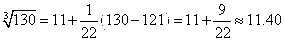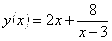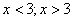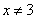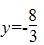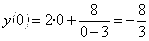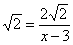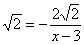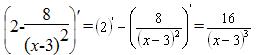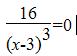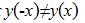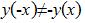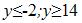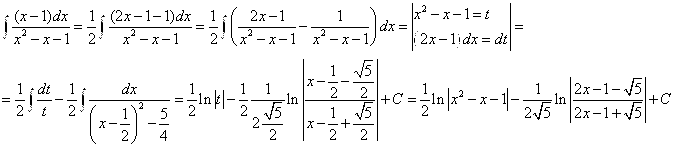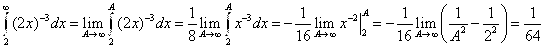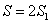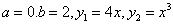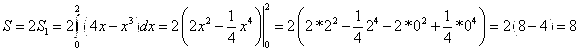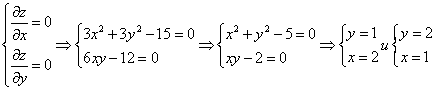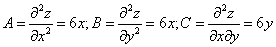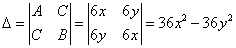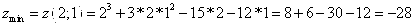Уравнение прямой проходящей через вершину

Г) уравнение прямой, проходящей через вершину параллельно стороне .

Решение:

Координаты векторов находим по формуле:

здесь X,Y координаты вектора; x_i, y_i — координаты точки А_i; x_j, y_j — координаты точки А_j

Например, для вектора AB

X = -1-1 = -2; Y = -2-2 = -4

=(-2;-4)

=(3;-7)

=(5;-3)

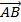
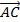
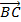
а) Длина стороны

Ответ:

б) Уравнение прямой

Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями:

Уравнение прямой AB

Каноническое уравнение прямой:

y = 2x или y -2x = 0

Ответ: или y = 2x или y -2x = 0

в) Угол

Найдем угол между векторами AB(-2;-4) и AC(3;-7)

γ = arccos(0.65) = 49.77 0

Ответ: 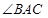= 49,77 0

г) Уравнение параллельной прямой AB, проходящей через точку С(4,-5)

Уравнение прямой AB: y = 2x

Уравнение СN параллельно AB находится по формуле:

Подставляя x₀ = 4, k = 2, y₀ = -5 получим:

y = 2x -13 или y -2x +13 = 0

Ответ: y = 2x -13 или y -2x +13 = 0

Задание. 4. Даны координаты точек 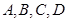. Требуется:

а) составить канонические уравнения прямой ;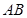

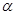
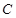
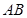
б) составить уравнение плоскости , проходящей через точку перпендикулярно прямой ;

в) составить уравнение плоскости 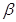, проходящей через точки ;

Дата добавления: 2015-04-20 ; просмотров: 11 | Нарушение авторских прав

Уравнение прямой проходящей через вершину

Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут

Неправильный логин или пароль.

Укажите электронный адрес и пароль.

Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.

Инструкция по изменению пароля отправлена на почту.

Чтобы зарегистрироваться, укажите ваш email и пароль

Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.

Уравнение прямой проходящей через вершину c параллельно ab

Уравнение прямой проходящей через вершину c параллельно ab

Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут

Неправильный логин или пароль.

Укажите электронный адрес и пароль.

Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.

Инструкция по изменению пароля отправлена на почту.

Чтобы зарегистрироваться, укажите ваш email и пароль

Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.

Элементы линейной алгебры и аналитической геометрии, графики, матрицы, пределы, мнк

Элементы линейной алгебры и аналитической геометрии

Задания 1-10. Даны координаты точек: А(х1;у1), В(х2;у2), С(х3;у3).

Значения координат точек приведены в таблице к этому заданию.

А) длину отрезка АВ;

Б) уравнение прямых АВ и ВС, проведенных через точки А, В и В, С соответственно;

В) угол θ между прямыми АВ и ВС;

Г) расстояние от точки С до прямой АВ. Уравнение перпендикуляра к прямой АВ, проходящего через точку С. Координаты точки пересечения прямой АВ и перпендикуляра;

Д) уравнение прямой, проходящей через точку С параллельно прямой АВ;

Е) построить чертеж, на котором показать заданные точки, угол θ и прямые.

Координаты векторов находим по формуле: X = xj — xi; Y = yj — yi

Здесь X, Y координаты вектора; xi, yi — координаты точки Аi; xj, yj — координаты точки Аj

Для вектора AB X = x2 — x1; Y = y2 — y1

X = 11—1 = 12; Y = -5-4 = -9

А) длина отрезка АВ

Длина вектора a(X;Y) выражается через его координаты формулой:

Б) Уравнение прямой

Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями:

Уравнение прямой AB

Каноническое уравнение прямой:

Уравнение прямой BC

Каноническое уравнение прямой:

В) угол θ между прямыми АВ и ВС;

Угол между векторами a1(X1;Y1), a2(X2;Y2) можно найти по формуле: 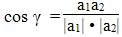где a1a2 = X1X2 + Y1Y2

Найдем угол между сторонами BA и BC

γ = arccos(0.45) = 63.440

Г) расстояние от точки С до прямой АВ. Уравнение перпендикуляра к прямой АВ, проходящего через точку С. Координаты точки пересечения прямой АВ и перпендикуляра;

Длина высоты треугольника, проведенной из вершины C

Расстояние d от точки M1(x1;y1) до прямой Ax + By + С = 0 равно абсолютному значению величины:

Найдем расстояние между точкой C(15;17) и прямой AB (4y + 3x — 13 = 0)

Уравнение высоты через вершину C

Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой

Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:

Найдем точку пересечения с прямой AB:

Имеем систему из двух уравнений:

Из первого уравнения выражаем y и подставим во второе уравнение.

Получаем: x = 3, y = 1

Д) уравнение прямой, проходящей через точку С параллельно прямой АВ;

Уравнение прямой, проходящей через данную точку С(x1, y1) в данном направлении, определяемом угловым коэффициентом k, y — y1 = k(x — x1).

Это уравнение определяет пучок прямых, проходящих через точку С(x1, y1), которая называется центром пучка. А k — это коэффициент при х уравнения прямой АВ

Тогда получим

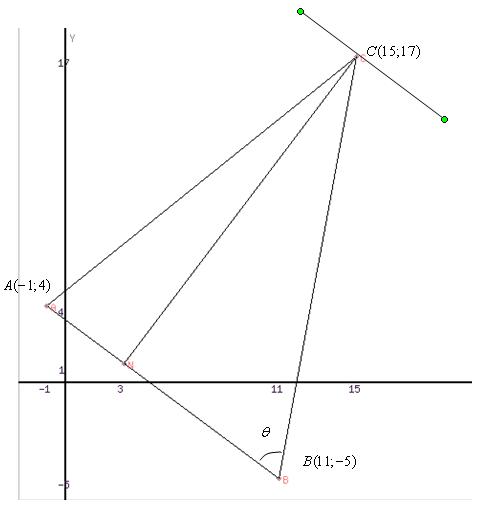
Е) построим чертеж

Задания 11-20. Решить систему уравнений двумя способами (по формулам Крамера и методом Гаусса)

№12.

По формулам Крамера.

Запишем систему в виде:

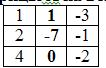
∆ = 1 • (-3 • (-2)-1 • (-1))-2 • (2 • (-2)-1 • (-3))+4 • (2 • (-1)-(-3 • (-3))) = -35 = -35

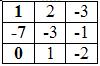
Заменим 1-ый столбец матрицы А на вектор результата В.

Найдем определитель полученной матрицы.

∆1 = 1 • (-3 • (-2)-1 • (-1))-(-7 • (2 • (-2)-1 • (-3)))+0 • (2 • (-1)-(-3 • (-3))) = 0

Заменим 2-ый столбец матрицы А на вектор результата В.

Найдем определитель полученной матрицы.

∆2 = 1 • (-7 • (-2)-0 • (-1))-2 • (1 • (-2)-0 • (-3))+4 • (1 • (-1)-(-7 • (-3))) = -70

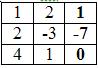
Заменим 3-ый столбец матрицы А на вектор результата В.

Найдем определитель полученной матрицы.

∆3 = 1 • (-3 • 0-1 • (-7))-2 • (2 • 0-1 • 1)+4 • (2 • (-7)-(-3 • 1)) = -35

Выпишем отдельно найденные переменные: , ,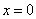

Запишем систему в виде расширенной матрицы:

Умножим 1-ую строку на (2). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:

Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:

Добавим 2-ую строку к 1-ой:

Теперь исходную систему можно записать как:

Из 1-ой строки выражаем z:

Из 2-ой строки выражаем у:

Из 3-ой строки выражаем x:

Введение в математический анализ.

Производная и ее приложения.

Задания 21-30. Найти указанные пределы, не пользуясь правилом Лопиталя:

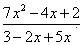
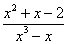
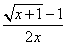
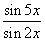
№22. а) ;б) ;в);г);д)

А) ;

Б) ;

В) ;

Г) ;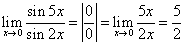

Использовали 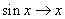при

Д)

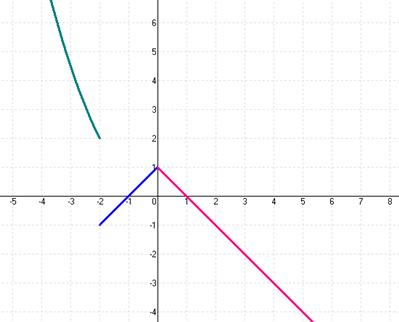
Задания 31-40. Задана функция y=ƒ(x). Найти все точки разрыва функции, если они существуют. Построить график функции.

№32.

Построим график данной функции:

Функция определена на всём множестве чисел и неэлементарная.

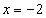
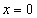
Каждая из составляющих функций непрерывна на своём промежутке; заданная функция может иметь точки разрыва только в точках смены аналитических выражений, то есть в точках и .

Исследуем поведение функции в этих точках: найдём значение функции в этих точках и пределы справа и слева,

, . Так как , Следовательно функция имеет разрыв 1-го рода – скачок.

, . Так как , то в этой точке функция в этой точке непрерывна

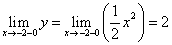
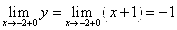
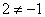
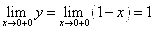
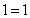
Задания 41-50. Найти производные первого порядка y’= 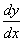функций:

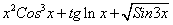
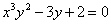
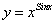
№42. а); б) ; в) ;

Д) ,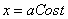

А) ;

Б) ;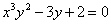

Дифференцируем обе части равенства по х:

Разрешаем равенство относительно :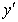

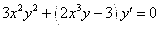
, тогда

Окончательно:

В) ;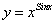

Прологарифмируем данную функцию:

Найдём производную от правой и левой части по х, считая у сложной функцией, зависящей от х.

Отсюда:

Д) ,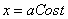

Находим и

Отсюда

Задания 51-60. Вычислить приближенно, заменяя приращение функции ее дифференциалом.

№52.

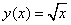
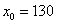
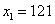
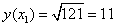
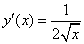
Рассмотрим функцию . Выберем, соответственно, , . Найдём значения функции и её производной:

, ,

Используя формулу для приближённых вычислений, 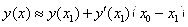, получим:

№Задания 61-70. Заданную функцию исследовать методами дифференциального исчисления. На основании результатов исследований построить график функции.

№62. ;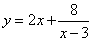

Исследуем функцию, заданную формулой:

Область определения:

Полученное решение отметим на рисунке.

Точки пересечения с осью : нет

, , — нет решений.

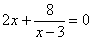
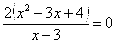
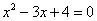
Точки пересечения с осью у:

Пусть х=0:

Вертикальные асимптоты: х=3

Горизонтальные асимптоты: нет.

Наклонные асимптоты: у=2х.

Предел разности исходной функции и функции 2х на бесконечности равен нулю.

Первая производная:

==

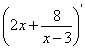
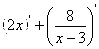
Критические точки: х=1, х=5

Случай.

Следующее уравнение равносильно предыдущему.

, , х-3=2, х=5

Случай .

Следующее уравнение равносильно предыдущему.

, , , х=1

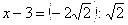
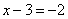
Вторая производная:

Возможные точки перегиба: нет

Точки разрыва: х=3

Симметрия относительно оси ординат: нет

Симметрия относительно начала координат: нет

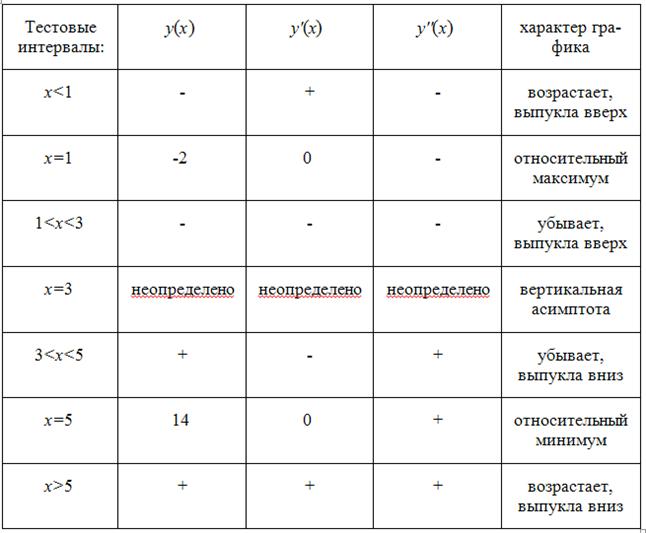
Результаты исследования функции занесем в таблицу.

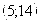
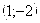
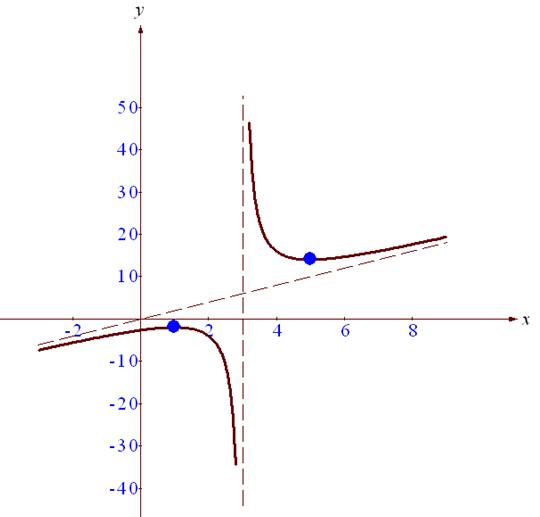
Относительный минимум . Относительный максимум .

Данные таблицы нанесем на координатную плоскость.

Используя результаты исследования функции, построим ее график.

Множество значений функции:

Наименьшее значение: нет

Наибольшее значение: нет

Задания 71-80. Найти интегралы.

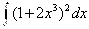
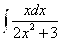
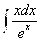
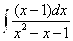
№72. а) ; б) ; в) ; г) ;

А) ;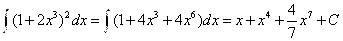

Б) ;

В) ;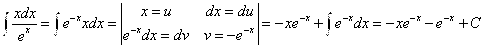

Г)

Задания 81-90. Вычислить несобственный интеграл или показать его расходимость

№82. ;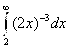

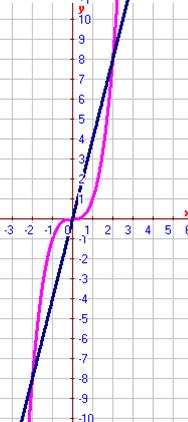
Задания 91-100. Найти площадь фигуры, ограниченной заданными линиями. Сделать рисунок.

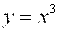
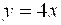
№92. и ;

Данные линии ограничивают две одинаковые по площади фигуры.

Тогда будем искать площадь одной части. Имеем

По формуле 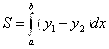. В нашем случае

Тогда

Ответ: 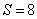кв. ед.

Функции нескольких переменных

Задания 101-110. Исследовать на экстремум функцию.

№102. ;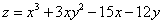

Необходимое условие существования єкстремума

, — критические точки, подозрительные на экстремум.

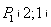
Используем достаточные условия экстремума

Найдем

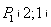
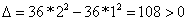
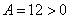
Для точки , — экстремум есть, а так как то в т. — минимум

Для точки , — экстремума нет.

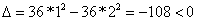
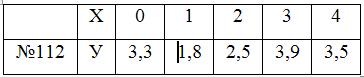
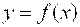
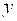
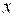
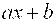
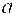
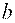
Задания 111-120. Экспериментально получены значения функции при пяти значениях аргумента, которые записаны в таблице. Предполагая, что между и имеется линейная зависимость, методом наименьших квадратов найти эмпирическую формулу (вычислить параметры и )

Линейное уравнение тренда имеет вид y = bt + a

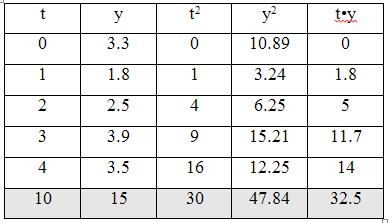
1. Находим параметры уравнения методом наименьших квадратов.

Система уравнений метода наименьших квадратов:

Для наших данных система уравнений имеет вид:

10a0 + 30a1 = 32.5

Из первого уравнения выражаем а0 и подставим во второе уравнение

Прямая на плоскости. Примеры решений

Решение проводим с помощью калькулятора.
Даны координаты треугольника: A(2,1), B(1,-2), C(-1,0).
1) Координаты векторов
Координаты векторов находим по формуле:
X = x_j — x_i; Y = y_j — y_i
здесь X,Y координаты вектора; x_i, y_i — координаты точки А_i; x_j, y_j — координаты точки А_j
Например, для вектора AB
X = x₂ — x₁; Y = y₂ — y₁
X = 1-2 = -1; Y = -2-1 = -3
AB(-1;-3)
AC(-3;-1)
BC(-2;2)
2) Модули векторов
Длина вектора a(X;Y) выражается через его координаты формулой:




3) Угол между прямыми
Угол между векторами a₁(X₁;Y₁), a₂(X₂;Y₂) можно найти по формуле:

где a₁a₂ = X₁X₂ + Y₁Y₂
Найдем угол между сторонами AB и AC

γ = arccos(0.6) = 53.13 0
4) Проекция вектора
Проекцию вектора b на вектор a можно найти по формуле:

Найдем проекцию вектора AB на вектор AC

5) Площадь треугольника
Пусть точки A₁(x₁; y₁), A₂(x₂; y₂), A₃(x₃; y₃) — вершины треугольника, тогда его площадь выражается формулой:

В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Решение. Принимая A за первую вершину, находим:

Пример. Даны координаты вершин треугольника АВС: А(–3; –1), В(4; 6), С(8; –2).
Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

Задание. Даны координаты вершин треугольника ABC: A(7;4), B(-9;-8), C(-2;16). Требуется:

1. составить уравнение медианы, проведенной из вершины B, и вычислить ее длину.
2. составить уравнение высоты, проведенной из вершины A, и вычислить ее длину.
3. найти косинус внутреннего угла B треугольника ABC.

Пример №3. Даны вершины A(1;1), B(7;4), C(4;5) треугольника. Найти: 1) длину стороны AB ; 2) внутренний угол A в радианах с точностью до 0,001. Сделать чертеж.
Скачать

Пример №4. Даны вершины A(1;1), B(7;4), C(4;5) треугольника. Найти: 1) уравнение высоты, проведенной через вершину C ; 2) уравнение медианы, проведенной через вершину C ; 3) точку пересечения высот треугольника; 4) длину высоты, опущенной из вершины C. Сделать чертеж.
Скачать

Пример №5. Даны вершины треугольника ABC: A(-5;0), B(7;-9), C(11;13). Определите: 1) длину стороны AB ; 2) уравнение сторон AB и AC и их угловые коэффициенты; 3) площадь треугольника.

Задание. Найти острый угол между прямыми x + y -5 = 0 и x + 4y — 8 = 0 .
Рекомендации к решению. Задача решается посредством сервиса Угол между двумя прямыми.
Ответ: 30.96 o

Пример №1. Даны координаты точек А1(1;0;2), A2(2;1;1), А3(-1;2;0), A4(-2;-1;-1). Найти длину ребра А1А2. Составить уравнение ребра А1А4 и грани А1А2А3. Составить уравнение высоты опущенной из точки А4 на плоскость А1А2А3. Найти площадь треугольника А1A2A3. Найти объем треугольной пирамиды А1A2А3A4.

Задание. По координатам вершин пирамиды А1,А2,А3,А4 найти: 1) длины ребер А1А2 и А1А3; 2) угол между ребрами А1А2 и А1А3; 3) площадь грани А1А2А3;4) объем пирамиды А1А2А3А4
A₁(3;5;4,0,0), A₂(8;7;4,0,0), A₃(5;10;4,0,0), A₄(4;7;9,0,0):Пример №10

Пример. В декартовой прямоугольной системе координат даны вершины пирамиды A, B, C, D. Найдите длину ребра AB, косинус угла между векторами, уравнение ребра, уравнение грани, уравнение высоты.
Решение

Пример. Даны вершины треугольника А(1, –1, -3), В(2, 0, -10), С(3, 0, -2).
а) Найти уравнение биссектрисы и высоты данного треугольника, проведенных из вершины A .
б) Найти уравнения всех его медиан и координаты точки их пересечения.
см. также Как найти периметр треугольника