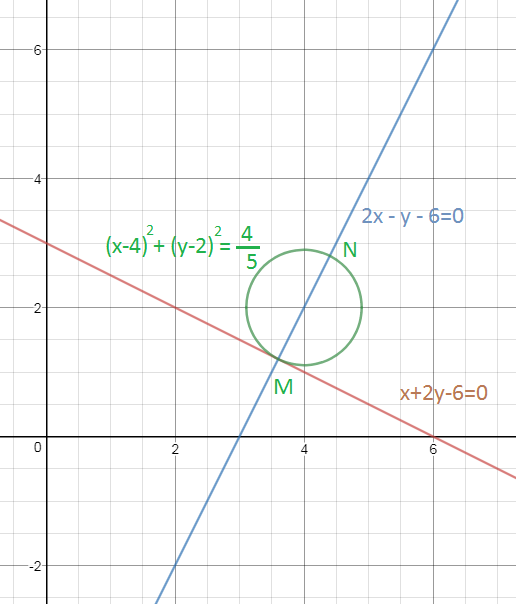Уравнение прямой симметричной относительно плоскости

Задача 27867 4.2.78) Составить уравнение прямой.

Условие

4.2.78) Составить уравнение прямой, симметричной прямой x+2y-6 = 0 относительно точки А(4; 2).

Решение

1 способ
Прямая, симметричная данной, параллельна данной.
Значит ее уравнение имеет вид
x+2y- d=0
Чтобы найти d подставим координаты точки, принадлежащей этой прямой, например точки Е.
Для этого выберем точку F(2;2), принадлежащую данной прямой и найдем координаты точки Е симметричной относительно А
Е(6;2)
6+2*2-d=0
d=10

2 способ
Составим уравнение прямой, перпендикулярной данной и проходящей через точку А
vector_(данной прямой)=(1;2)
vector_(перпендикулярной прямой)=(2;-1)
Скалярное произведение этих векторов равно 0, векторы ортогональны.
2х-у+с=0
Чтобы найти c подставляем координаты точки А
2*4-2=с
с=-6
2х — у — 6 = 0

Найдем расстояние от точки А до данной прямой
d=|4+2*2-6|/sqrt(1+2^2)=2/sqrt(5)

Составим уравнение окружности с центром в точке А и радиусом R=2/sqrt(5).
Эта окружность касается данной прямой и второй прямой, параллельной данной и находящейся на расстоянии 2/sqrt(5) от точки.
(x-4)^2+(y-2)^2=4/5

(x-4)^2+(2x-6-2)^2=4/5
(x-4)^2=4/25
x-4=2/5 или х-4=-2/5
х=4,4 или х=3,6 — абсцисса точки М
у=2х-6=2*4,4-6=2,8
N(4,4; 2,8)

Прямая, параллельная данной имеет вид
х + 2y — d = 0
Чтобы найти d подставим координаты точки N
4,4+2*2,8 — d=0

О т в е т. х+2y -10 =0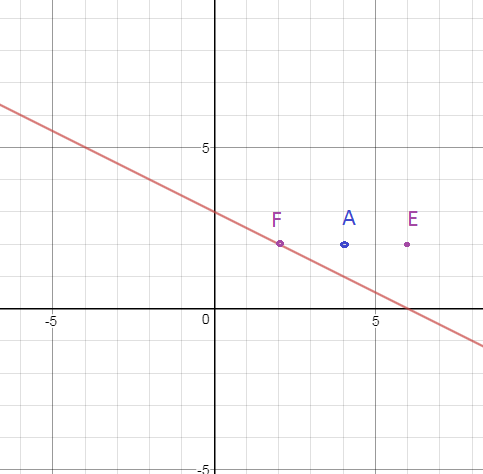

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок №5. Метод преобразований решения задач

Перечень вопросов, рассматриваемых в теме:

• симметрия относительно произвольной плоскости;
• понятие «метод движений» в пространстве.

Глоссарий по теме

Метод геометрических преобразований

Сущность метода геометрических преобразований при решении геометрических задач заключается в привлечении того или иного геометрического преобразования, опираясь на свойства которого, задача может быть решена.

Метод параллельного переноса

Сущность этого метода состоит в том, что наряду с данными и искомыми фигурами рассматриваются некоторые другие фигуры, которые получаются из данных или искомых фигур или их частей путём переноса на некоторый вектор.

Применение симметрии к решению задач на построение называют методом симметрии. Метод симметрии состоит в том, что наряду с данными и искомыми фигурами рассматриваются также фигуры, симметричные некоторым из них относительно некоторой точки/оси/плоскости.

Идея метода поворота состоит в том, чтобы повернуть какую-либо данную или искомую фигуру около целесообразно избранного центра/оси на соответствующий угол так, чтобы облегчить проведение анализа задачи или даже непосредственно прийти к решению.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255, сс. 121-126.

Шарыгин И.Ф., Геометрия. 10–11 кл.: учеб. для общеобразоват. учреждений /– М.: Дрофа, 2009. – 235,: ил., ISBN 978–5–358–05346–5, сс. 178-196. Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. учреждений– М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Метод геометрических преобразований

Сущность метода геометрических преобразований при решении геометрических задач заключается в привлечении того или иного геометрического преобразования, опираясь на свойства которого, задача может быть решена.

1.1. Метод параллельного переноса.

Сущность этого метода состоит в том, что наряду с данными и искомыми фигурами рассматриваются некоторые другие фигуры, которые получаются из данных или искомых фигур или их частей путём переноса на некоторый вектор.

Этим путём иногда удаётся облегчить проведение анализа. Метод параллельного переноса применяют главным образом для объединения разрозненных частей фигур, когда часто построение фигуры становится затруднительным только от того, что части этой фигуры слишком удалены друг от друга, и потому трудно ввести в чертёж данные. В этих случаях какую-нибудь часть искомой фигуры переносят параллельно самой себе на такое расстояние, чтобы вновь полученная фигура могла быть построена или непосредственно, или легче, чем искомая фигура. Направление такого переноса зависит от условий задачи и должно быть выбрано так, чтобы во вновь полученную фигуру вошло, по возможности, большое количество данных.

1.2. Метод симметрии.

Применение осевой симметрии к решению задач на построение называют методом симметрии. Метод симметрии состоит в том, что наряду с данными и искомыми фигурами рассматриваются также фигуры, симметричные некоторым из них относительно некоторой оси. При удачном выборе оси и преобразуемой фигуры решение задачи может значительно облегчиться, а в некоторых случаях симметрия непосредственно даёт искомые точки.

Метод симметрии заключается в следующем. Предполагают задачу решённой и одну из данных точек (прямую или окружность) отражают в какой-нибудь известной оси; иногда эта ось проходит через известную точку. Тогда полученную симметричную точку (прямую или окружность) подчиняют тем же условиям, которым должна была удовлетворять заменённая точка (прямая или окружность). После этого получится новая задача, которую решают способами, уже нам известными. Обыкновенно, с решением этой новой задачи предложенная задача уже будет решена сама собой, и только в редких случаях придётся ещё переходить к первоначальным условиям задачи. Таким образом, метод симметрии приводит решение предложенной задачи к решению новой задачи.

1.3. Метод поворота.

Поворотом также пользуются как методом решения геометрических задач на построение. Идея метода вращения состоит в том, чтобы повернуть какую-либо данную или искомую фигуру около целесообразно избранного центра/оси на соответствующий угол так, чтобы облегчить проведение анализа задачи или даже непосредственно прийти к решению.

2. Решение задач методом преобразований

2.1. Симметрия относительно произвольной плоскости

Постановка задачи. Найти координаты точки , симметричной точке , относительно плоскости Ax + By + Cz + D = 0.

1. Находим уравнение прямой, которая перпендикулярна данной плоскости и проходит через точку . Так как прямая перпендикулярна заданной плоскости, то в качестве ее направляющего вектора можно взять вектор нормали плоскости, т.е. .

Поэтому уравнение прямой будет:

2. Находим точку пересечения прямой и плоскости Ax + By + Cz + D = 0.

Для этого обозначим и выразим x, y, z:

.

Подставим x, y, z в уравнение плоскости:

найдем значение t.

Затем найдем x, y, z. Найденные координаты будут являться координатами точки .

3. Точка является серединой отрезка , где точка является точкой симметричной точке , поэтому

, , .

Задача 1. Найти точку M’, симметричную точке M относительно плоскости.

M(1, 1, 1), x + 4y + 3z + 5 = 0.

Уравнение прямой, которая проходит через точку M перпендикулярно заданной плоскости будет:

.

Найдем точку пересечения прямой и плоскости.

,

,

(1 + t) + 4(1 + 4t) + 3(1 + 3t) + 5 = 0,

Откуда – точка пересечения прямой и плоскости. является серединой отрезка MM’, поэтому

,

,

,

Даны плоскость α: x + 2y – z – 2 = 0 и две точки А(1, -2, -3) и В (-1, -1, -2). Найдите на этой плоскости точку С такую, чтобы ломаная АСВ имела наименьшую длину.

Данная плоскость пересекает оси координат в точках

Две заданные точки лежат по одну сторону от данной плоскости.

Если бы две точки лежали по разные стороны от плоскости α, то очевидно, искомой точкой С была бы точка пересечения отрезка, концами которого являются данные точки, с плоскостью α, а ломаная выродилась бы в отрезок.

Сведем нашу задачу к описанной ситуации.

Для этого найдем точку, симметричную любой из заданных относительно данной плоскости α.

Например, точке А.

Используя решение задачи 1, получим следующую последовательность действий.

Уравнение прямой, которая проходит через точку А перпендикулярно заданной плоскости будет:

.

Найдем точку пересечения полученной прямой и плоскости α.

.

.

(1 + t) + 2(2t – 2) — (-t– 2) – 2 = 0

Откуда точка пересечения прямой, перпендикулярной плоскости α и проходящей через точку А, с плоскость α . Точка пересечения прямой и плоскости. является серединой отрезка АА’, поэтому

,

,

,

Теперь найдем точку пересечения отрезка A’B с плоскостью α.

Прямая A’B имеет направляющий вектор .

Уравнение прямой A’B:

.

Найдем точку пересечения полученной прямой и плоскости α.

.

.

.

Таким образом, координаты искомой точки .

Ответ: .

Примеры и разбор решения заданий тренировочного модуля

1. Напишите уравнение образа плоскости 2x + 5y – z – 5 = 0 при симметрии относительно плоскости Oxz.

Найдем координаты двух точек плоскости 2x + 5y – z – 5 = 0, лежащих в плоскости Oxz. Для этого найдем точки плоскости, принадлежащие осям координат.

OX: z = y = 0, x = 2,5 A(2,5; 0; 0)

OZ: x = y = 0, z = -5 B(0; 0; -5).

Эти точки принадлежат и образу плоскости 2x + 3y – z – 5 = 0 при симметрии относительно плоскости Oxz.

Теперь найдем точку данной плоскости, принадлежащую оси ординат.

OY: z = x = 0, y = 2,5 С(0; 1; 0).

Точка, симметричная точке С относительно плоскости Oxz, имеет координаты С'(0; -1; 0).

Теперь напишем уравнение плоскости через три полученные точки.

Параметрическое уравнение прямой. Параметрическое уравнение прямой в пространстве

Прямая вместе с точкой являются важными элементами геометрии, с помощью которых строятся многие фигуры в пространстве и на плоскости. В данной статье подробно рассматривается параметрическое уравнение прямой, а также его связь с другими типами уравнений для этого геометрического элемента.

Прямая и уравнения для ее описания

Прямая в геометрии представляет собой совокупность точек, которые соединяют произвольные две точки пространства отрезком с наименьшей длиной. Этот отрезок является частью прямой. Любые другие кривые, соединяющие зафиксированные две точки в пространстве, будут иметь большую длину, поэтому прямыми не являются.

Вам будет интересно: Нейтральная лексика — это. Определение, понятие, значение и примеры

На рисунке выше показаны две черные точки. Синяя линия, соединяющая их, является прямой, а красная — кривой. Очевидно, что длина красной линии между черными точками больше, чем синей.

Существуют несколько видов уравнений прямой, с помощью которых можно описать прямую в трехмерном пространстве или в двумерном. Ниже приведены названия этих уравнений:

• векторное;
• параметрическое;
• в отрезках;
• симметричное или каноническое;
• общего типа.

Вам будет интересно: А. Пушкин «Песнь о вещем Олеге»: жанр и идея

В данной статье рассмотрим параметрическое уравнение прямой, однако выведем его из векторного. Также покажем связь параметрического и симметричного или канонического уравнений.

Уравнение векторное

Понятно, что все приведенные типы уравнений для рассматриваемого геометрического элемента связаны между собой. Тем не менее векторное уравнение является базовым для всех них, поскольку оно непосредственно следует из определения прямой. Рассмотрим, как оно вводится в геометрию.

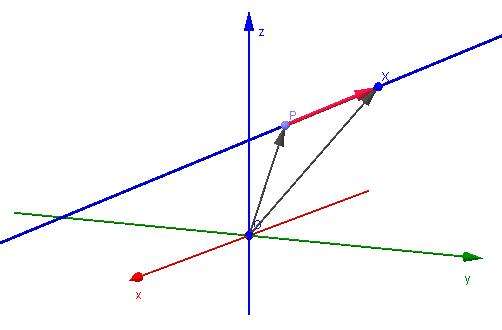
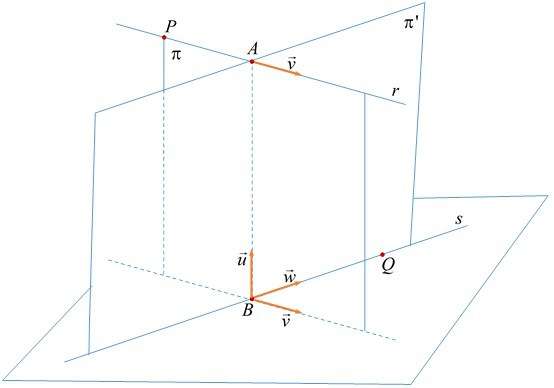
Допустим, дана точка в пространстве P(x0; y0; z0). Известно, что эта точка принадлежит прямой. Сколько прямых можно провести через нее? Бесконечное множество. Поэтому для того, чтобы можно было провести единственную прямую, необходимо задать направление последней. Направление, как известно, определяется вектором. Обозначим его v¯(a; b; c), где символы в скобках — это его координаты. Для каждой точки Q(x; y; z), которая находится на рассматриваемой прямой, можно записать равенство:

(x; y; z) = (x0; y0; z0) + α × (a; b; c)

Здесь символ α является параметром, принимающим абсолютно любое действительное значение (умножение вектора на число может изменить только его модуль или направление на противоположное). Это равенство называется векторным уравнением для прямой в трехмерном пространстве. Изменяя параметр α, мы получаем все точки (x; y; z), которые образуют эту прямую.

Вам будет интересно: Тайны «Аненербе»: история, артефакты, архивы

Стоящий в уравнении вектор v¯(a; b; c) называется направляющим. Прямая не имеет конкретного направления, а ее длина является бесконечной. Эти факты означают, что любой вектор, полученный из v¯ с помощью умножения на действительное число, также будет направляющим для прямой.

Что касается точки P(x0; y0; z0), то вместо нее в уравнение можно подставить произвольную точку, которая лежит на прямой, и последняя при этом не изменится.

Рисунок выше демонстрирует прямую (синяя линия), которая задана в пространстве через направляющий вектор (красный направленный отрезок).

Не представляет никакого труда получить подобное равенство для двумерного случая. Используя аналогичные рассуждения приходим к выражению:

(x; y) = (x0; y0) + α × (a; b)

Видим, что оно полностью такое же, как и предыдущее, только используются две координаты вместо трех для задания точек и векторов.

Уравнение параметрическое

Сначала получим в пространстве параметрическое уравнение прямой. Выше, когда записывалось векторное равенство, уже упоминалось о параметре, который в нем присутствует. Чтобы получить параметрическое уравнение, достаточно раскрыть векторное. Получаем:

Совокупность этих трех линейных равенств, в каждом из которых имеется одна переменная координата и параметр α, принято называть параметрическим уравнением прямой в пространстве. По сути, мы не сделали ничего нового, а просто явно записали смысл соответствующего векторного выражения. Отметим лишь один момент: число α, хотя и является произвольным, но оно для всех трех равенств одинаковое. Например, если α = -1,5 для 1-го равенства, то такое же его значение следует подставить во второе и в третье равенства при определении координат точки.

Параметрическое уравнение прямой на плоскости подобно таковому для пространственного случая. Оно записывается в виде:

Таким образом, чтобы составить параметрическое уравнение прямой, следует записать в явном виде векторное уравнение для нее.

Получение уравнения канонического

Как выше было отмечено, все уравнения, задающие прямую в пространстве и на плоскости, получаются одно из другого. Покажем, как получить из параметрического уравнения прямой каноническое. Для пространственного случая имеем:

Выразим параметр в каждом равенстве:

Поскольку левые части являются одинаковыми, тогда правые части равенств тоже равны друг другу:

(x — x0) / a = (y — y0) / b = (z — z0) / c

Это и есть каноническое уравнение для прямой в пространстве. Значение знаменателя в каждом выражении является соответствующей координатой направляющего вектора. Значения в числителе, которые вычитаются из каждой переменной, представляют собой координаты точки, принадлежащей этой прямой.

Соответствующее уравнение для случая на плоскости примет вид:

(x — x0) / a = (y — y0) / b

Дальше в статье решим несколько задач, используя полученные знания.

Уравнение прямой через 2 точки

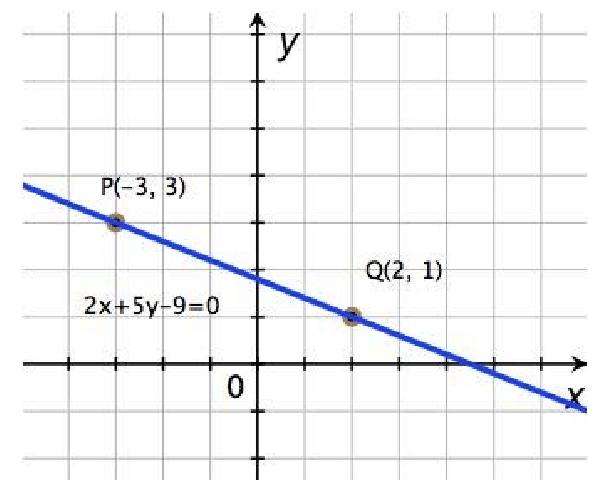
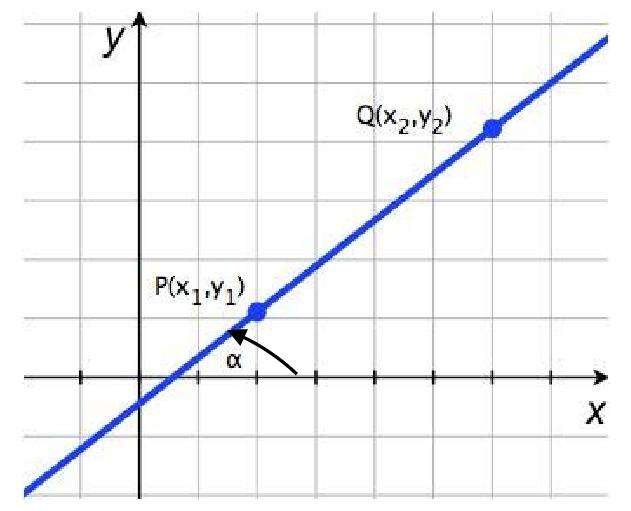
Известно, что две фиксированные точки как на плоскости, так и в пространстве однозначно задают прямую. Предположим, что заданы две следующие точки на плоскости:

Как составить уравнение прямой через них? Для начала следует определить направляющий вектор. Его координаты имеют следующие значения:

PQ¯(x2 — x1; y2 — y1)

Теперь можно записать уравнение в любом из трех видов, которые были рассмотрены в пунктах выше. Например, параметрическое уравнение прямой принимает вид:

x = x1 + α × (x2 — x1);

y = y1 + α × (y2 — y1)

В канонической форме можно переписать его так:

(x — x1 ) / (x2 — x1) = (y — y1) / (y2 — y1)

Видно, что в каноническое уравнение входят координаты обеих точек, причем в числителе можно менять эти точки. Так, последнее уравнение можно переписать следующим образом:

(x — x2) / (x2 — x1) = (y — y2) / (y2 — y1)

Все записанные выражения называются уравнениями прямой через 2 точки.

Задача с тремя точками

Даны координаты следующих трех точек:

Необходимо определить, лежат эти точки на одной прямой или нет.

Решать эту задачу следует так: сначала составить уравнение прямой для любых двух точек, а затем подставить в него координаты третьей и проверить, удовлетворяют ли они полученному равенству.

Составляем уравнение через M и N в параметрической форме. Для этого применим полученную в пункте выше формулу, которую обобщим на трехмерный случай. Имеем:

Теперь подставим в эти выражения координаты точки K и найдем значение параметра альфа, который им соответствует. Получаем:

1 = 5 + α × (-3) => α = 4/3;

-1 = 3 + α × (-1) => α = 4;

-5 = -1 + α × 1 => α = -4

Мы выяснили, что все три равенства будут справедливы, если каждое из них примет отличающееся от других значение параметра α. Последний факт противоречит условию параметрического уравнения прямой, в котором α должны быть равны для всех уравнений. Это означает, что точка K прямой MN не принадлежит, а значит, все три точки на одной прямой не лежат.

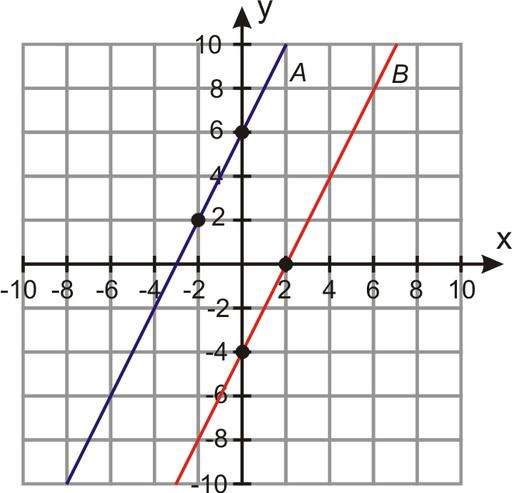
Задача на параллельность прямых

Даны два уравнения прямых в параметрическом виде. Они представлены ниже:

Необходимо определить, являются ли прямые параллельными. Проще всего определить параллельность двух прямых с использованием координат направляющих векторов. Обращаясь к общей формуле параметрического уравнения в двумерном пространстве, получаем, что направляющие вектора каждой прямой будут иметь координаты:

Два вектора являются параллельными, если один из них можно получить путем умножения другого на некоторое число. Разделим попарно координаты векторов, получим:

Это означает что:

Направляющие вектора v2¯ и v1¯ параллельны, значит, прямые в условии задачи тоже являются параллельными.

Проверим, не являются ли они одной и той же прямой. Для этого нужно подставить координаты любой точки в уравнение для другой. Возьмем точку (-1; 3), подставим ее в уравнение для второй прямой:

-1 = 2 — 6 × λ => λ = 1/2;

3 = 4 — 3,6 × λ => λ ≈ 0,28

То есть прямые являются разными.

Задача на перпендикулярность прямых

Даны уравнения двух прямых:

Перпендикулярны ли эти прямые?

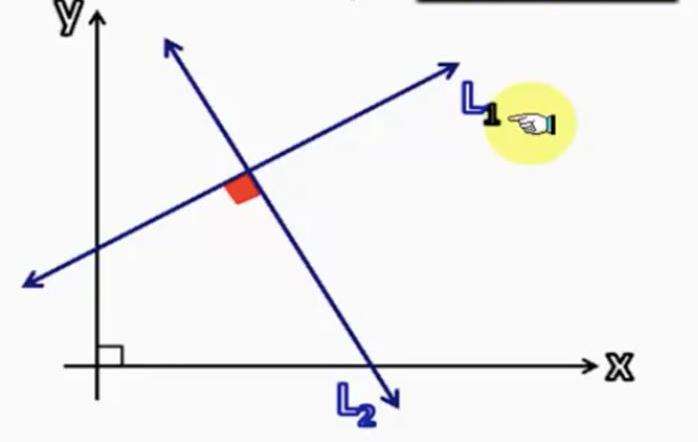
Две прямые будут перпендикулярны, если скалярное произведение их направляющих векторов равно нулю. Выпишем эти вектора:

Найдем их скалярное произведение:

(v1¯ × v2¯) = 2 × 6 + 3 × (-4) = 12 — 12 = 0

Таким образом, мы выяснили, что рассмотренные прямые перпендикулярны. Они изображены на рисунке выше.