Уравнение прямой угловой коэффициент прямой 9 класс

Презентация по геометрии Мерзляк 9 класс. Угловой коэффициент в уравнении прямой

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Угловой коэффициент
в уравнении прямой

Какие из следующих утверждений верны?
I. 1. Площадь квадрата равна произведению двух его смежных сторон.
2. Диагональ трапеции делит её на два равных треугольника.
3. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
II. 1. Существует прямоугольник, который не является параллелограммом.
2. Треугольник с углами 40°, 70°, 70° — равнобедренный.
3. Если из точки M проведены две касательные к окружности и А и В — точки касания, то отрезки MA и MB равны.
III 1. Если в четырёхугольнике две стороны параллельны, то этот четырёхугольник — параллелограмм. 2. Через любые три точки плоскости, не лежащие на одной прямой, проходит единственная окружность.
IV. 1. Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2. Любой квадрат является ромбом.
3. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
V. 1. Если один из двух смежных углов острый, то другой тупой.
2. Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны..
3. Все хорды одной окружности равны между собой.

Какие из следующих утверждений верны?
VI. 1. Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники равны.
2. Сумма смежных углов равна 180°.
3. Любая медиана равнобедренного треугольника является его биссектрисой.
VII. 1. Вертикальные углы равны. 2. Две прямые, параллельные третьей прямой, перпендикулярны друг другу. 3. Диагонали любого прямоугольника делят его на 4 равных треугольника.
VIII. 1. Если радиус окружности равен 7, а расстояние от центра окружности до прямой равно 5, то эти прямая и окружность не имеют общих точек.
2. Сумма двух противоположных углов четырёхугольника равна 180. 3. Центр окружности, описанной около прямоугольного треугольника, лежит на стороне этого треугольника.
IX. 1. Диагонали любого прямоугольника равны.
2. Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
3 Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
X 1. Внешний угол треугольника равен сумме двух внутренних углов этого треугольника.
2. Центром вписанной в треугольник окружности является точка пересечения биссектрис этого треугольника.
3. Биссектрисы соседних углов параллелограмма взаимно перпендикулярны.

№ 1.
Найти расстояние между точками А и В,
если А(0;0), В(-5;12);

Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач

Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.

Угол наклона прямой и угловой коэффициент прямой

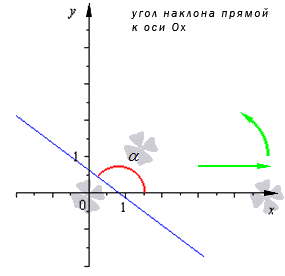
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.

Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.

Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .

Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.

Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.

Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.

Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.

Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .

Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .

Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .

Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .

Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .

Ответ: α = a r c t g 3 .

Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .

Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:

α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .

Ответ: 5 π 6 .

Уравнение с угловым коэффициентом

Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .

Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.

Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.

Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.

Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.

Ответ: М 1 принадлежит прямой, а М 2 нет.

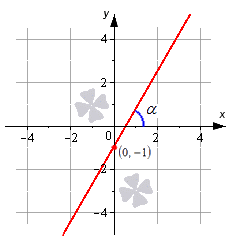
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .

Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку

Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .

Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .

Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .

Решение

По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .

Ответ: y = — 2 x + 7 .

Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .

По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:

y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно

Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.

Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .

Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.

Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.

Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:

y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3

Ответ: x 1 = y — 12 — 3 .

Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.

Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?

Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:

y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0

Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .

Решим задачу обратную данной.

Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .

Результат и является уравннием с угловым коэффициентом, который равняется — A B .

Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.

Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:

2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .

Ответ: y = 1 6 x + 1 4 .

Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:

x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .

Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1

Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.

Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:

y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .

Ответ: y = 3 2 x — 3 .

Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.

Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:

5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x

Ответ: y = 5 2 x — 6 .

Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.

Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .

Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:

x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .

Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:

x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1

Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .

Презентация урока по теме «Уравнение прямой»
презентация к уроку по геометрии (9 класс) на тему

ПЛАН-КОНСПЕКТ УРОКА «Уравнение прямой».

Тип урока урок изучения нового материала.

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Самостоятельная работа I вариант II вариант 1) Определите координаты центра и радиус окружности, заданной уравнением: а)(х+8) 2 +(у-5) 2 =16 а)(х-4) 2 + (у+2) 2 =4 б)х 2 +(у-10) 2 =25 б)(х+7) 2 + у 2 =9 2) Напишите уравнение окружности радиуса r с центром А, если: а) А(0; 5), r=3; а) А(-1; 2), r=2; б) А(-3; -7), r=6; б) А(4; -3), r=10 3) Напишите уравнение окружности с центром в начале координат, проходящей через заданную точку В(-4; 3) А(-6;8)

4 ) Составить уравнение окружности

Ответы 1 вариант 2 вариант 1 а) (- 8;5) r=4 б) (0;10) r=5 1 а) (4;-2) r=2 б) (-7;0) r= 3 2 а) х 2 +(у-5) 2 =9 б) (х+3) 2 +(у+7) 2 =36 2 а) (х+1) 2 +(у-2) 2 =4 б) (х-4) 2 +(у+3) 2 =100 3 х 2 +у 2 =25 3.х 2 +у 2 =100 4 (х-2) 2 +(у-2) 2 =4 4 (х-4) 2 +(у-3) 2 =25

Китайская пословица гласит: » Я слушаю, — я забываю ; Я вижу, — я запоминаю ; Я делаю, — я усваиваю.»

Практическое задание Начертите прямоугольную систему координат. Проведите произвольную прямую d . Отметьте точки А(х 1; у 1 ) и В(х 2 ;у 2 ) так, чтобы прямая d была серединным перпендикуляром к отрезку АВ. Отметьте на прямой d точку N ( х;у ) и постройте отрезки А N и В N . Получили А N = В N (почему?) или А N 2 = В N 2 . Напишите формулу расстояния между точками А и N , В и N .

Уравнение прямой ( х-х 1 ) 2 + (у-у 1 ) 2 =(х-х 2 ) 2 +(у-у 2 ) 2

после преобразований : 2х(х 1 -х 2 )+2у(у 1 -у 2 )+(х 2 2 +у 2 2 -х 1 2 -у 1 2 )=0 ах+ву+с=0 – уравнение прямой , где а=2х(х 1 -х 2 ), в=2у(у 1 -у 2 ), с = х 2 2 +у 2 2 -х 1 2 -у 1 2

1. Уравнение прямой В прямоугольной системе координат уравнение прямой имеет вид: ах+ву+с=0, где а,в,с — некоторые числа

2. Частные случаи расположения прямой: а ) а=0 , b ≠0, у = m

2.Частные случаи расположения прямой б) а ≠0 , b =0 , х= n

2. Частные случаи расположения прямой: в) а≠0, b ≠0 , с=0, у=кх

3. Уравнение прямой, не параллельной оси ординат Если а≠0, b≠0 , то уравнение ах+ b у+с=0 можно представить в виде у =кх+ m , где к=-а / b , m =-с / b

геометрический смысл коэффициента k Возьмем две точки на прямой А(х 1 ;у 1 ) и В(х 2 ;у 2 ), где х 1 Мне нравится