Уравнение прямой, проходящей через две точки онлайн
С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через две точки. Дается подробное решение с пояснениями. Для построения уравнения прямой задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точек в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение прямой, проходящей через две точки − примеры и решения
Пример 1. Построить прямую, проходящую через точки A(2, 1, 1), B(3, 1, -2).
 | (1) |
Подставив координаты точек A и B в уравнение (1), получим:
 |
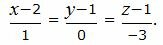 |
(Здесь 0 в знаменателе не означает деление на 0).
Составим параметрическое уравнение прямой:
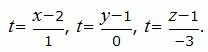 |
Выразим переменные x, y, z через параметр t :
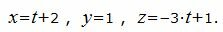 |
Каноническое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:
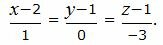 |
Параметрическое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:
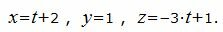 |
Пример 2. Построить прямую, проходящую через точки A(1, 1/5, 1) и B(−2, 1/2, −2).
 | (2) |
Подставив координаты точек A и B в уравнение (2), получим:
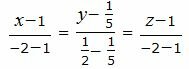 |
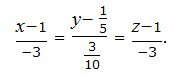 |
Составим параметрическое уравнение прямой:
 |
Выразим переменные x, y, z через параметр t :
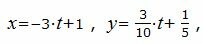 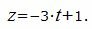 |
Каноническое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:
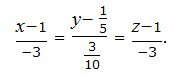 |
Параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:
Разработка урока по теме «Уравнение прямой».
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Геометрия – 9 класс Урок № 14
Тема: «Уравнение прямой».
вывести уравнение прямой и показать, как можно использовать это уравнение при решении геометрических задач;
закрепить умения и навыки по теме «Уравнение окружности»;
подготовка к ГИА.
– Распознать уравнение окружности и уравнение прямой по предложенному уравнению, научить обучающихся составлять уравнение окружности и уравнение прямой по готовому чертежу, строить окружность и прямую по заданному уравнению.
— Формулы уравнений окружности и прямой и уметь их применять при решении задач.
— Формирование критического мышления и навыков работы в группе.
— Содействовать в ходе урока воспитанию решительности, смелости при выполнении заданий, самостоятельности.
— Развитие памяти, логического мышления обучающихся при решении задач.
— Развитие умения составлять алгоритмические предписания и умение действовать в соответствии с предложенным алгоритмом.
– Видеть проблему и наметить пути её решения.
– Кратко излагать свои мысли устно и письменно.
Тип урока: усвоения новых знаний.
Оборудование: ПК, мультимедийный проектор, экран.
Сообщение темы и целей урока. Отчет старосты класса об отсутствующих. Проверка готовности к класса к уроку.
II. Актуализация опорных знаний.
Проверка выполнения домашнего задания. Разбор нерешенных заданий.
1. Лежит ли точка А (2; –1) на окружности, заданной уравнением (x – 2) 2 + (y – 3) 2 = 25?
2. Напишите уравнение окружности, если ее центр – точка (4; 5), а радиус равен 3.
3. Напишите уравнение окружности с центром в начале координат, если она проходит через точку С (–2; 3).
4. Найдите длину вектора <–12; 5>.
5. Найдите координаты середины отрезка PQ, если Р (5; –3); Q (3; –7).
6. Найдите координаты вектора , если А (2; –5), В (–3; 4).
1. Лежит ли точка А (2; –1) на прямой, заданной уравнением 2х – 3y – 7 = 0?
2. Напишите уравнение окружности, если ее центр – точка (4; 5), а радиус равен 2.
3. Напишите уравнение окружности с центром в точке Р (–2; –1), если она проходит через точку Q (1; 3).
4. Найдите расстояние между точками А (–1; 3) и В (2; –1).
5. Найдите координаты вектора, равного сумме векторов и, если <–12; 5>, <7; –3>.
6. Найдите координаты вектора , если С (–1; 6), D (3; –2).
III . Изучение нового материала.
Для выведения уравнения прямой проведем эту прямую как серединный перпендикуляр к некоторому отрезку с данными координатами конечных точек отрезка.
Все точки серединного перпендикуляра находятся на равных расстояниях от концов отрезка.
Рис. 1. Серединный перпендикуляр к отрезку
Пусть 









Возведем в квадрат выражения в скобках и приведем подобные слагаемые:
Введем новые обозначения:
Следовательно, уравнение прямой будет иметь следующий вид:

На рис. 2 изображены вертикальные прямые, уравнение которых выглядят следующим образом:
а) 

б) 

в) 


Рис. 2. Вертикальные прямые

На рис. 3 изображены горизонтальные прямые, уравнения которых выглядят следующим образом:
а) 

б) 

в) 


Рис. 3. Горизонтальные прямые
Уравнение наклонной прямой к оси 

Введем новые обозначения:
Таким образом, уравнение наклонной к оси 






1. Дано уравнение прямой: 
В этом случае 



Рис. 4. Прямая
2. Дано уравнение прямой: 
В этом случае 



Рис. 5. Прямая
Даны две прямые:
1. Данные прямые будут параллельными, если выполняются следующие условия:
То есть эти прямые должны быть наклонены под одним углом к оси 

2. Данные прямые будут перпендикулярными, если выполняется следующее условие:
Дана точка 






Задавая коэффициент 
Дано : прямая 

Найти : а) уравнение прямой, которая проходит через точку 

Все наклонные прямые, которые проходят через точку 
1. Угловые коэффициенты параллельных прямых равны. Поэтому уравнение прямой, проходящей через точку 

2. Произведение угловых коэффициентов перпендикулярных прямых равно 

Подставляем данный коэффициент в уравнение прямых, проходящих через точку 
Ответ : а) 

Дано : точка 

Найти : уравнение прямой 
Уравнение прямой имеет вид:
Необходимо определить числа 




Решим эту систему, выразив 


Подставим это значение в равенство
Найденные значения 

При 


Мы получили уравнение прямой, которая проходит через две данные точки ( 

Это уравнение наклонной прямой, которая имеет угловой коэффициент 



Определим координаты точки пересечения прямой с осью 

Следовательно, координаты точки пересечения прямой с осью 


Рис. 6. Иллюстрация к задаче
Ответ : 


Дано : точка 

Найти : уравнение серединного перпендикуляра к отрезку 
Рис. 7. Иллюстрация к задаче
Пусть 



Подставим в данное равенство соответствующие координаты:
Разделим обе части уравнения на 4 и получим искомое уравнение серединного перпендикуляра:
Ответ : 
Уравнение прямой в отрезках
Пусть 




Такое уравнение называется уравнением прямой в отрезках . В данном случае отрезок 

Дано : точка 

Найти : уравнение прямой 
Уравнение прямой в отрезках выглядит следующим образом:
В данном случае: 

Ответ : 
Уравнение прямой, проходящей через две точки.
Дано : точки 


Требуется : вывести уравнение наклонной прямой 
Рис. 11. Наклонная прямая, проходящая через две точки
Подставляем координаты первой точки в уравнение наклонной прямой:
Получаем систему уравнений:
Вычтем из первого уравнения второе:
Необходимо найти 
Вычтем из первого уравнения второе:
Ответ : 


1. Учитель объясняет решение задачи:
напишите уравнение прямой, проходящей через две данные точки Р (2; 1) и Q (–3; –1).
Уравнение прямой PQ имеет вид ax + by + c = 0. Так как точки P и Q лежат на прямой PQ, то их координаты удовлетворяют этому уравнению:
2cx – 5cy + c = 0 |: c 
Ответ: 2x – 5y + 1 = 0.
2. Самостоятельно по учебнику обучающиеся разбирают решение задачи № 972 (а), с. 245.
3. Решить задачу № 973 на доске и в тетрадях.
4. Решить задачу № 975.
Пересечение прямой с осью OX: y = 0, тогда 3x – 4 ∙ 0 + 12 = 0; 3x = –12; x = –4; точка А (–4; 0);
пересечение прямой с осью OY: x = 0, тогда 3 ∙ 0 – 4y + 12 = 0; –4y = –12; y = 3; точка В (0; 3).
5. Решить задачу № 976 (повторить при решении способ сложения систем уравнений):
Точка пересечения прямых D (3; –2).
6. Решить задачу № 977.
Прямая, проходящая через точку М (2; 5) и параллельная оси OX, имеет вид: y = 5; прямая, параллельная оси OY, записывается уравнением: х = 2.
7. Самостоятельное решение обучающимися задачи № 978.
8. Решить устно задачи:
1) Окружность задана уравнением (x – 1)2 + y2 = 9. Назвать уравнение прямой, проходящей через ее центр и параллельной оси ординат.
Центр О (1; 0) и параллельная оси OY прямая x = 1.
2) Окружность задана уравнением (x + 1)2 + (y – 2)2 = 16. Назвать уравнение прямой, проходящей через ее центр и параллельной оси абсцисс.
Центр А (–1; 2); прямая y = 2 параллельна оси OX.
V . Подведение итогов урока.
С чем мы сегодня познакомились на уроке?
Назовите общий вид уравнения прямой.
Какое уравнение имеет прямая параллельная ОХ, ОУ?
VI . Домашнее задание: прочитать п. 95, ответить на вопросы с.249, выполнить № 972(а,б), № 979.
Уравнение прямой 9 класс
Уравнение прямой 9 класс презентация к уроку
Просмотр содержимого документа
«Уравнение прямой 9 класс»
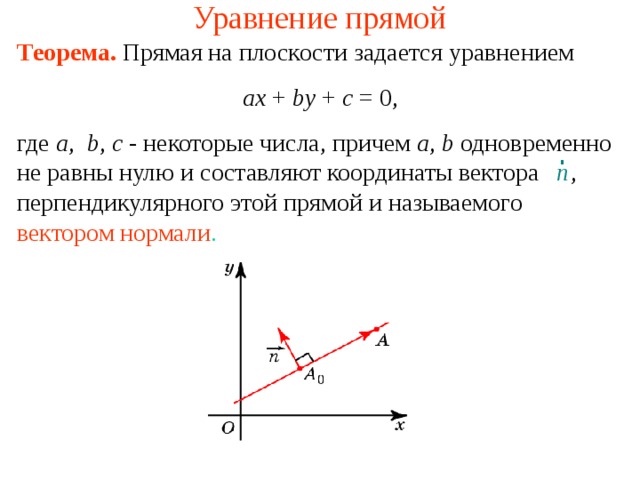
Теорема. Прямая на плоскости задается уравнением
где a , b , c — некоторые числа, причем a , b одновременно не равны нулю и составляют координаты вектора , перпендикулярного этой прямой и называемого вектором нормали .
В режиме слайдов ответы появляются после кликанья мышкой
Если число b в уравнении прямой не равно нулю , то, разделив на b , это уравнение можно привести к виду y = kx + l . Коэффициент k называется угловым коэффициентом этой прямой. Он равен тангенсу угла , который образует прямая с осью абсцисс .
В режиме слайдов ответы появляются после кликанья мышкой
Взаимное расположение прямых
Д ве прямы е , заданны е уравнениями a 1 x + b 1 y + c 1 = 0, a 2 x + b 2 y + c 2 = 0, параллельны, если векторы их нормалей одинаково или противоположно направлены, т.е. для их координат ( a 1 , b 1 ), ( a 2 , b 2 ) для некоторого числа t выполняются равенства a 2 = ta 1 , b 2 = tb 1 . При этом, если с 2 = t с 1 , то уравнения определяют одну и ту же прямую. Если же с 2 tc 1 , то эти уравнения определяют параллельные прямые.
Е сли две прямые пересекаются, то угол между ними равен углу между их нормалями ( a 1 , b 1 ), ( a 2 , b 2 ). Этот угол можно вычислить через формулу скалярного произведения
В режиме слайдов ответы появляются после кликанья мышкой
Найдите угол между прямыми, заданными уравнениями : x + 2 y – 1 = 0, 2 x – y + 3 = 0.
Решение: Векторы нормалей к данным прямым имеют координаты (1, 2) и (2, -1) соответственно. Их скалярное произведение равно нулю и, следовательно, эти векторы перпендикулярны. Значит, угол между данными прямыми равен 90 о .
В режиме слайдов ответы появляются после кликанья мышкой
Найдите уравнение прямой, проходящей через заданные точки A 1 ( x 1 , y 1 ) и A 2 ( x 2 , y 2 ).
Решение: Найдем вектор нормали к данной прямой. Он перпендикулярен вектору ( x 2 – x 1 , y 2 – y 1 ). Следовательно, в качестве такого вектора можно взять вектор с координатами ( y 2 – y 1 , x 1 – x 2 ). Искомым уравнением прямой будет уравнение
которое можно также переписать в виде
В режиме слайдов ответы появляются после кликанья мышкой
Какие уравнения имеют координатные прямые: а) Ox ; б) Oy ?
В режиме слайдов ответы появляются после кликанья мышкой
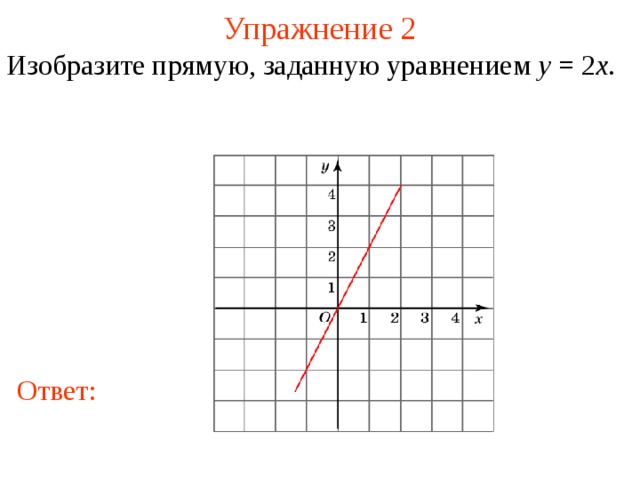
Изобразите прямую , заданную уравнением y = 2 x .
В режиме слайдов ответы появляются после кликанья мышкой
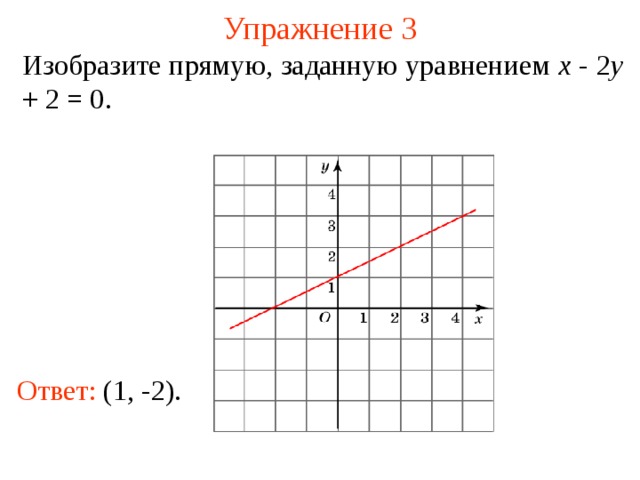
Изобразите прямую , заданную уравнением x — 2 y + 2 = 0.
В режиме слайдов ответы появляются после кликанья мышкой
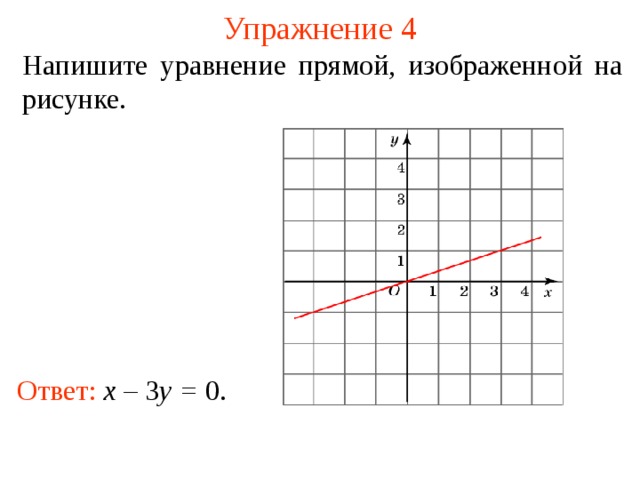
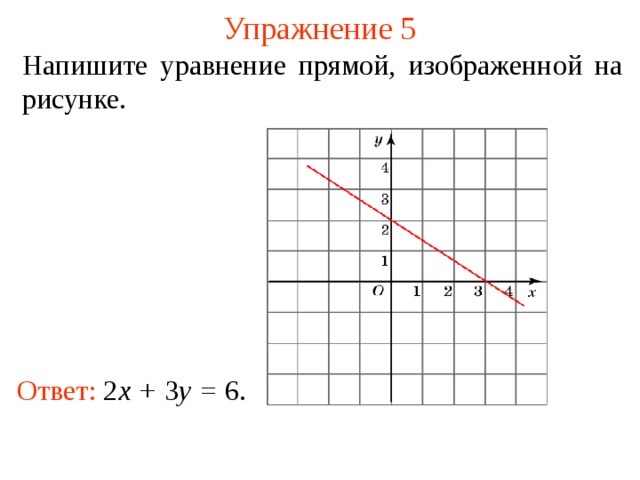
Напишите уравнение прямой, изображенной на рисунке.
В режиме слайдов ответы появляются после кликанья мышкой
Напишите уравнение прямой, изображенной на рисунке.
В режиме слайдов ответы появляются после кликанья мышкой
Напишите уравнение прямой, проходящей через начало координат с угловым коэффициентом: а) k = 1; б) k = 2; в) k = 0,5 ; г) k = -1; д) k = -2; е) k = — 0,5 . Нарисуйте эти прямые.
В режиме слайдов ответы появляются после кликанья мышкой
Найдите угловой коэффициент прямой: а) 2 x — 3 y + 4 = 0; б) x + 2 y — 1 = 0.
В режиме слайдов ответы появляются после кликанья мышкой
Напишите уравнение прямой, проходящей через точки A (1, 0), B (0, 1).
В режиме слайдов ответы появляются после кликанья мышкой
Напишите уравнение прямой, проходящей через точку A 0 (1, 2) с вектором нормали (-1, 1).
В режиме слайдов ответы появляются после кликанья мышкой
Напишите уравнение прямой, проходящей через точки M (3, -1), N (4, 1). Найдите координаты вектора нормали этой прямой.
Ответ: 2 x — y — 7 = 0; (2, -1).
В режиме слайдов ответы появляются после кликанья мышкой
Напишите уравнение прямой, которая проходит через точку M (1, -2) и параллельна: а) координатной прямой Ox ; б) координатной прямой Oy ; в) прямой y = x .
В режиме слайдов ответы появляются после кликанья мышкой
Точка H (-2, 4) является основанием перпендикуляра, опущенного из начала координат на прямую. Напишите уравнение этой прямой.
Ответ: x — 2 y + 10 = 0.
В режиме слайдов ответы появляются после кликанья мышкой
Определите, какие из перечисленных ниже пар прямых параллельны между собой:
г) 2 x + 4 y — 8 = 0, — x — 2 y + 4 = 0.
В режиме слайдов ответы появляются после кликанья мышкой
Найдите угол между прямыми, заданными уравнениями x + y + 1 = 0, x — y — 1 = 0. Изобрази те эти прямые.
В режиме слайдов ответы появляются после кликанья мышкой
Найдите координаты точки пересечения прямых:
б) 3 x — y + 2 = 0, 5 x — 2 y + 1 = 0.
В режиме слайдов ответы появляются после кликанья мышкой
Напишите уравнение прямой, симметричной прямой, заданной уравнением ax + by + с = 0, относительно: а) оси Ox ; б) оси Oy ; в) начала координат O .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: а ) ax – by + с = 0 ;
Треугольник задан своими вершинами A (1, 3), B (3, 0), C (4, 2). Найдите уравнения высот этого треугольника и координаты их точки пересечения.
В режиме слайдов ответы появляются после кликанья мышкой
http://infourok.ru/razrabotka-uroka-po-teme-uravnenie-pryamoy-1442042.html
http://multiurok.ru/files/uravnenie-priamoi-9-klass.html