Уравнение прямой в пространстве в аффинных координатах

47. Аффинная система координат на прямой, плоскости и в пространстве

В случае прямой базис состоит из одного ненулевого вектора V = (V) и система координат (О, V) изображена на рис. 4.1. В системе координат на прямой каждая точка A прямой имеет одну координату A(X), определяему разложением вектора По базису, = XV. Тогда A(0), E(1), где V = .

Систему координат на прямой можно задать еще следующими способами:

Двумя различными точками О и E данной прямой. Тогда одну из точек, например О, берем в качестве начала системы координат, а в качестве базисного вектора возьмем вектор V = (см. рис. 4.2).

Точкой О, единичным отрезком ОE и положительным направлением данной прямой, которое отмечается стрелкой.

2Аффинная система координат на плоскости. В случае плоскости базис состоит из двух неколлинеарных векторов плоскости, V = (V1, V2), и система координат (О, V1, V2) изображена на рис. 4.3. В системе координат на плоскости каждая точка A плоскости имеет две координаты A(X, Y), определяемые разложением вектора По базису, = XV1+ YV2. Тогда A(0, 0), E1(1, 0), E2(0, 1), где V1 = , V2 = . Координаты точки называются соответственно Абсциссой и Ординатой.

Систему координат на плоскости можно задать еще следующими способами:

Тремя точками О, E1, E2 плоскости, не лежащими на одной прямой. Тогда одну из точек, например О, берем в качестве начала системы координат, а в качестве базисного вектора возьмем векторы V1 = , V2 = .

Двумя пересекающимися числовыми осями ОX, ОY данной плоскости с общим началом О. Ось ОX называется Осью абсцисс, ось ОY — Осью ординат.

Аффинная система координат (О, V1, V2) называется Правой (Левой), если поворот от вектора к вектору по кратчайшему направлению совершается против часовой стрелки (по часовой стрелке). На рис. 4.3 и 4.4 представлены правые системы координат.

3. Аффинная система координат в пространстве. В случае пространства базис состоит из двух некомпланарных векторов пространства, V = (V1,V2, V3), и система координат (О, V1, V2, V3) изображена на рис. 4.5. В этой системе координат каждая точка A пространства имеет три координаты A(X,Y,Z), определяемые разложением вектора по базису, = XV1+ YV2 + ZV3. Тогда A(0, 0, 0), E1(1, 0, 0), E2(0, 1, 0), E3(0, 0, 1), где V1 = , V2 = , V3 = . Координаты точки называются соответственно Абсциссой, ординатой и Аппликатой.

Истему координат в пространстве можно задать еще следующими способами:

Четверкой точек О, E1, E2, E3 пространства, не лежащими на одной плоскости. Тогда одну из точек, например О, берем в качестве начала системы координат, а в качестве базисного вектора возьмем векторы V1 = , V2 = , V3 = .

Тремя числовыми осями ОX, ОY, ОZ, не лежащими в одной плоскости с общим началом О. Ось ОX называется Осью абсцисс, ось ОY — Осью ординат, ось ОZ — Осью аппликат.

Аффинная система координат (О, V1, V2, V3) называется Правой (Левой), если тройка векторов V1, V2, V3 правая (левая) На рис. 4.5 и 4.6 представлены правые системы координат, а на рис. 4.7 левая система координат.

Аффинные координаты

Аффинная система координат на прямой, на плоскости, в пространстве

Пусть в пространстве фиксирована точка . Совокупность точки и базиса называется аффинной (декартовой) системой координат :

– аффинная система координат на прямой (рис.2.1,а) — это точка и ненулевой вектор на прямой (базис на прямой);

– аффинная система координат на плоскости (рис.2.1,6) — это точка и два неколпинеарных вектора , взятые в определенном порядке (базис на плоскости);

– аффинная система координат в пространстве (рис.2.1,в) — это точка и три некомпланарных вектора , взятые в определенном порядке (базис в пространстве).

Точка называется началом координат . Прямые, проходящие через начало координат в направлении базисных векторов, называются координатными осями: — ось абсцисс, — ось ординат, — ось аппликат . Плоскости, проходящие через две координатные оси, называются координатными плоскостями .

Аффинная система координат в пространстве (или на плоскости) называется правой, если ее базис является правым, и левой, если её базис — левый.

Координаты векторов и точек в аффинной системе координат

Координатами вектора в заданной системе координат называются, как и ранее, коэффициенты в разложении вектора по базису (см. разд.1.3.1; 1.3.2; 1.3.3).

Для любой точки в заданной аффинной системе координат можно рассмотреть вектор начало которого совпадает с началом координат, а конец — с точкой (рис.2.1,а,б,в). Этот вектор называется радиус-вектором точки .

Координатами точки в заданной системе координат называются координаты радиус-вектора этой точки относительно заданного базиса. В пространстве это координаты вектора в базисе , т.е. коэффициенты в разложении (рис.2.1,в). Координаты точки записывают в виде . Первая координата называется абсциссой , вторая – ординатой , третья – аппликатой . На плоскости и на прямой координаты записывают в виде и согласно разложениям (рис.2.1,6), (рис.2.1,а). Координаты точки , или, что то же самое, координаты ее радиус-вектора представляют в виде координатного столбца (матрицы-столбца):

Найдем координаты вектора с началом в точке и концом в точке . Рассмотрим треугольник (рис.2.2). Радиус-векторы и представляются в виде , . По правилу треугольника (см. разд. 1.1.2) вычитания векторов получаем , т.е. вектор имеет координаты . Этим доказано следующее правило: чтобы найти координаты вектора,нужно из координат его конца вычесть соответствующие координаты его начала . Это же правило справедливо для аффинных систем координат на плоскости и на прямой.

1. В заданной системе координат каждой точке можно поставить в соответствие её координаты, причем это соответствие взаимно однозначное:

В частности, разным точкам соответствуют разные наборы координат.

2. Если вектор с координатами отложить от точки , то конец вектора будет иметь координаты .

3. Координаты точки , которая делит отрезок в отношении , находятся по координатам его концов и :

В частности, координаты середины отрезка равны среднему арифметическому соответствующих координат концов отрезка :

Координаты точки которая «делит» площадь треугольника в отношении 0,\,\beta>0,\,\gamma>0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAKgAAAAVBAMAAAAgMbgsAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAAX1bEJvBQdDnITGx8wJf6wAAAnVJREFUOMvFVc9rE0EYfZNMNpp42BJ/BQkEokKwC6HYg5LAklLwIhQtpakIKSZGxMC2SEBpwBgLFRW0NpeKsAg99BCIB28GcrI9eKla8WD/F2fnxyYbsoWCYg6Z2f1m3rzvfW++Bf7Pj+h/ByfysD8P3307FD3z8ZCt9LFf4Et6xuU5qXdtTzTYKnT800qPl0ZHQkW67hLtIZHxROudwIYvaHAT84NypdyHdgaGetBsdC2Gfd5dtwv6bQhqwlSz4z3UBznkmwrIsGCoyBaQdsbagkrwJ8jvYX5PFWo7ieuOdNmy0IzkVei2hXpS8V++8I5ParfEiygDPZDH58smrjpbYy2pO9uXKALXXpzaCAjlpyRqdQC0dPGeKBpZqQiR+6D01UGDPhGOkMwMBroI+tyk+2fForHYqj0ESho4+V0pUdG9oNrsuWYgo5xnOcsd0D0E2Ja1CSVObNX0goYZTbcsW00v6Gdg5bQqRHSuI5m+QfwHA3nm+rpsCk1zEpQRIb6gTrVdPhEOmuPpJ5gmVVVqqfdA9TUTYTf9O7qs/i+37priE55bcoZuEu0er1VVYcpCdTPEsCMcNmHihLT6pwrh4xroPqakUUIzKkWLj3Hu09BrTL+PCYMoS2k9tBDnBB8lSVpYo7Yjj851ApswihJUZBSUxQe7bAUTdHd8Z/urML9yMH2ZLUFzbipJPSjMwmN+hNYLGVzZEw/HdFFf1R7G5icdW9MlEM7lpu7KH7zE/pa5TSOiJYUX+vfnw2V22qKYb+vea4poyjys/6WETX0amfA8yR6t49KGtOnoRibdceNojZpf3ZjlE52W4/1/8a2xR738AxcTjszkPv2OAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, находятся по координатам его вершин :

В частности, координаты точки пересечения медиан треугольника равны среднему арифметическому соответствующих координат вершин треугольника :

Эти формулы следуют из свойств 2,4 аффинных и выпуклых комбинаций (см. разд. 1.6.1). Они остаются справедливыми и на координатной плоскости, если аппликаты всех точек положить равными нулю. Например, координаты середины отрезка , или координаты точки пересечения медиан треугольника

Пример 2.1. В некоторой аффинной системе координат известны координаты вершин треугольной пирамиды (см. рис.2.3): Найти координаты (в той же системе координат):

а) точки пересечения медиан треугольника ;

б) точки , которая делит отрезок в отношении .

Решение. Учитывая пункт 3 замечаний 2.1, получаем:

Прямая в пространстве – виды уравнения прямой в пространстве

Прямая в пространстве – это линия, которая проходит от одной точки к другой, а также за пределы этих точек в бесконечность. Есть несколько видов уравнения прямой в пространстве: каноническое, параметрическое, угол между двумя прямыми в пространстве и т. д. Про это расскажем в данной статье и для наглядности предоставим несколько примеров.

Параметрическое и каноническое уравнение прямой в пространстве

Параметрическое и каноническое уравнение прямой рассматривается практически так, как и для прямой на плоскости. Значит, нужно составить уравнение прямой , которая проходит через данную точку параллельно направляющему вектору .

Пусть, – произвольная точка прямой, тогда векторы и коллинеарные, а это значит, что координаты их пропорциональны, поэтому получаем:

это и есть канонические уравнения прямой.

Приравнивая каждую из дробей (1) к параметру , запишем параметрические уравнения прямой:

Уравнение прямой в пространстве, которая проходит через две заданные точки

Уравнение прямой в пространстве – тема очень лёгкая, так как здесь самое важное – знать нужную формулу. Тогда легко можно решить любую задачу.

Итак, через две точки и можно не только геометрично провести линию, но и сложить её уравнения.

За направляющий вектор возьмём , тогда по формуле (1) у нас получается:

уравнение прямой в пространстве, которые проходят через две заданные точки.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Общее уравнение прямой – переход к каноническому уравнению

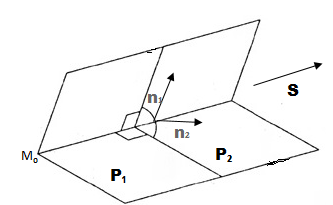
Объяснение про общее уравнение прямой начнём с прямой, которая задана двумя плоскостями, что пересекаются по этой прямой.

Пусть известны их уравнения:

Тогда система (4) называется общим уравнением прямой.

Чтобы перейти к каноническим уравнениям вида (1), необходимо найти вектор и точку этой прямой.

Точку находим, как один из решений системы (4). Например, положив в (4) находим , тогда и точку . Направляющий вектор , который параллелен к каждой из плоскостей и и перпендикулярен к их нормальным векторам и , то есть , . (см. рис. 1). Поэтому вектор можно найти при помощи векторного произведения и

= x =

Найдены координаты и подставим в каноническое уравнение (1).

Например, от общих уравнений прямой:

Перейдём к каноническим, положив в системе (при нём относительно больше коэффициенты). найдём . Нормальные векторы и . Тогда направляющий вектор

x = ,

и канонические уравнения станут:

Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых

Угол между двумя прямыми :

и

равен углу между их направляющими векторами и , поэтому

=

Условия параллельности и перпендикулярности прямых соответственно запишутся:

и .

Примеры решения задач

Давайте рассмотрим первый пример, где можно двумя способами построить прямую:

Задача

При точке и направляющем векторе необходимо:

1. составить каноническое уравнение прямой;
2. построить эту прямую.

Решение

1) По формуле (1) запишем каноническое уравнение прямой :

= .

2) Рассмотрим два способа построения прямой .

Первый способ

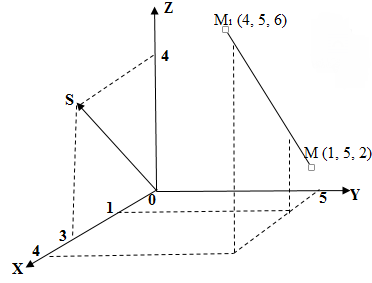
В системе координат строим вектор и точку и проводим через точку прямую параллельную вектору .

Второй способ

По формуле (2) запишем каноническое уравнение прямой в параметрическом виде:

На рисунке видно, что при произвольных значениях из системы находим координаты соответствующих точек, которые принадлежат прямой . Так при находим координаты . Через две точки и проводим прямую .

Очевидно, что найти острый угол между прямыми совершенно не сложно при знании темы и определённых формул. Давайте разберём такой пример:

Задача

Найти острый угол между прямыми:

,

Решение

По формуле (7) получаем:

= = =

Так как , тогда угол тупой, , а острый угол .

Ответ

.

Рассмотрим последний пример, где нужно составить уравнение. Здесь, как и в каждой задаче, важно знать и понимать, какой формулой нужно воспользоваться.

Задача

Составить уравнение прямой , которая проходит через точку и параллельна прямой .

Решение

От параметрического уравнения переходим к каноническому При условии параллельности прямых то есть направляющим вектором новой прямой может служить известный вектор и по формуле (1) у нас получается:

.

Ответ

.