Уравнение пуассона для электростатического поля в диэлектрике

1.15. Расчет одномерных электростатических полей по уравнениям Пуассона и Лапласа

Электростатическое поле в однородной среде с постоянной диэлектрической проницаемостью полностью характеризуется уравнением Пуассона (1.11) или (если в рассматриваемой области отсутствуют объемные связанные заряды) уравнением Лапласа (1.12).

Наиболее просто уравнения Пуассона и Лапласа решаются в случае одномерных полей, потенциалы которых зависят только от одной координаты. При этом дифференциальные уравнения в частных производных переходят в обыкновенные дифференциальные уравнения второго порядка, решение которых при известных граничных условиях является несложной задачей.

Так, в прямоугольной системе координат уравнения Пуассона и Лапласа для одномерного поля будут иметь следующий вид:

(1.22)

Решение уравнения (1.22), очевидно, может быть получено лишь тогда, когда объемная плотность заряда r и абсолютное значение диэлектрической проницаемости e заданы как функции координат во всем пространстве. Например, если объемная плотность r изменяется вдоль оси ОХ по закону

(где коэффициент а и показатель степени n являются постоянными), то, в случае, когда e=const, частное решение уравнения Пуассона будет иметь следующий вид:

где С₁ и С₂ – постоянныеинтегрирования, которые определяются из граничных условий.

В случае, когда объемная плотность заряда r также является постоянной величиной, решение имеет вид

Частное решение уравнения Лапласа (1.29) можно представить следующим образом:

В цилиндрической системе координат для одномерного поля вид уравнения Пуассона или Лапласа и их решение зависят от того, функцией какой координаты является искомый потенциал U. Например, если потенциал U зависит только от радиальной координаты r (U=U(r)), то уравнения (1.11) и (1.12) будут иметь вид

(1.26)

(1.27)

Решение уравнения (1.26) определяется видом функции r. Если, например, объемная плотность заряда r изменяется вдоль радиуса r по закону

то искомое решение будет иметь вид:

Для случая, когда объемная плотность заряда r не зависит от координаты r, решение уравнения (1.26) можно представить следующим образом:

Решение уравнения Лапласа (1.27) имеет вид:

Если искомый потенциал является функцией только одной угловой координаты j, то уравнения Пуассона и Лапласа приобретают следующий вид:

(1.31)

При постоянном значении r уравнение (1.31) имеет частное решение

.

Решение уравнение Лапласа (1.32) можно записать следующим образом:

В сферической системе координат для одномерного поля вид уравнения Пуассона или Лапласа и их решение зависят также от того, функцией какой координаты является искомый потенциал U.

Так, если потенциал U зависит только от радиальной координаты r, то уравнения Пуассона и Лапласа будут иметь вид:

При изменении объемной плотности заряда r по закону

,

решение уравнения (1.35) можно представить следующим образом:

Если r является постоянной величиной, решение будет иметь вид

Уравнение Лапласа (1.36) имеет следующее решение:

В случае, если потенциал U зависит только от одной координаты q, уравнение Лапласа (1.12) будет иметь вид

Решение этого уравнения можно представить следующим образом:

Если потенциал U является функцией только одной координаты j, то уравнение (1.12) будет иметь вид

а его решение является линейной функцией этой координаты

Пример 1. Плоский конденсатор с двумя слоями диэлектрика подключен к источнику постоянного напряжения U₀=100В (рис. 1.25). Относительные значения диэлектрической проницаемости слоев e_r1=3, e_r2=6. Толщина слоев – d₁=d₂=1мм.

Один из слоев заряжен с объемной плотностью r, которая изменяется по толщине по закону r=10 -4 х Кл/м 3 .

Пренебрегая краевым эффектом, найти распределение потенциала и напряженности поля в слоях диэлектрика.

Построить графики изменения потенциала и напряженности электрического поля вдоль оси ОХ.

Данная задача по расчету электрического поля является одномерной. В первом слое электрический потенциал отвечает уравнению Лапласа (1.23), а во втором – уравнению Пуассона (1.22). Решение этих уравнений можно представить с помощью выражений (1.24) и (1.25) , соответственно, при n=1 и а=1.

Для определения постоянных интегрирования используем граничные условия на внешних границах области и на границе раздела двух диэлектриков (внутренней границе).

Будем при этом считать, что правая пластина имеет нулевой потенциал.

Здесь D₁ и D₂ – нормальные составляющие вектора электрического смещения.

Из первого равенства следует, что С₂=U₀.

Перепишем три следующих граничных условия, подставляя в них соответствующие выражения для потенциалов и вектора электрического смещения:

Решая последнюю систему из трех уравнений относительно неизвестных С₁, С₃, и С₄, получим С₁=-66670,

Таким образом, окончательно выражения для напряженности поля и потенциалов можно записать в виде:

Графики изменения потенциала и напряженности поля представлены на рис. 1.26

На графике все значения представлены в относительных единицах, причем за базисные значения приняты значения потенциала и напряженности поля на поверхности левой пластины (Ub=100 В, Eb=66670 В/м).

Пример 2. Бесконечно длинный диэлектрический (e_r=4) полый цилиндр заряжен и находится в воздухе. Радиус внутренней поверхности цилиндра R₁=2мм, наружной – R₂=6мм (рис.1.27). Объемная плотность заряда r является функцией расстояния от оси цилиндра r=0.1r.

Найти законы изменения потенциала и напряженности поля в функции расстояния от оси цилиндра. Построить графики изменения указанных функций вдоль радиуса.

Решение. Поле в данном случае является одномерным, поскольку напряженность поля и потенциал зависят только от одной радиальной координаты.

При решении задачи по расчету электрического поля в заданной области, эту область необходимо разбить на три подобласти. В первой из них (0?r?R₁) поле отсутствует (Е=0). Во второй подобласти (R₁?r?R₂) электрический потенциал отвечает уравнению Пуассона (1.26), а в третьей (R₂? r??) – уравнению Лапласа (1.27), которые имеют решения (1.28) (при n=1,a=0.1) и (1.30).

Перепишем эти решения в следующем виде:

Здесь индексы у потенциалов обозначают их принадлежность ко второй и третьей подобластям.

Постоянные интегрирования определим из граничных условий, которые можно поставить как из классических граничных условий, так и из следующих соображений. Поскольку поле внутри цилиндра отсутствует, то при r=R₁, можно принять Е₂=0.

Отсюда сразу определяем постоянную С₁=7.533. Примем потенциал равным нулю на наружной поверхности цилиндра (U₂=0 при r=R₂), тогда

и, таким образом, С₂=106.335.

Потенциал U₃ со стороны третьей подобласти на этой же поверхности (r=R₂) также будет равен нулю.

Здесь же на границе раздела двух диэлектриков равны между собой нормальные составляющие векторов электрического смещения, а с учетом того, что в нашем случае вектор электрического смещения имеет одну составляющую, которая направлена по радиусу, то это означает, что на границе раздела равны между собой и сами векторы электрического смещения.

Перепишем последнее уравнение в следующем виде:

Решая совместно уравнения (1.42) и (1.43), находим постоянные интегрирования С₃=-783.427, С₄=-4008.

Таким образом, выражения для напряженности электрического поля и потенциала принимают вид

Потенциал в первой подобласти (внутри цилиндра) является величиной постоянной, равной значению потенциала со стороны второй подобласти на внутренней поверхности цилиндра.

График изменения потенциала и напряженности электрического поля представлен на рис. 1.28. Все значения на графике даны в относительных единицах. За базисное значение напряженности поля принято ее значение на наружной поверхности цилиндра E_b=130.6кВ/м.

В качестве базисного значения потенциала принято абсолютное значение потенциала на расстоянии 0.01м от оси цилиндра U_b=400.2В.

Это же расстояние r=0.01м принято за базисное значение радиальной координаты.

Пример 3. Цилиндрический бесконечно длинный конденсатор заполнен двухслойным диэлектриком, относительные значения диэлектрической проницаемости слоев которого равны соответственно e_r1=2 и e_r2=4.

Радиус внутренней жилы равен R₁=1мм, внутренний радиус наружной обкладки – R₃=4мм, радиус поверхности раздела слоев диэлектрика – R₂=2мм (рис. 1.29). К обкладкам конденсатора приложено постоянное напряжение Uо = 100 В. Один из диэлектриков заряжен (внутренний).

Объемная плотность заряда является функцией расстояния r от оси конденсатора r=аr 2 (а=10).

Определить закон изменения потенциала и напряженности электрического поля в каждом слое.

Построить графики изменения напряженности поля и потенциала вдоль радиуса.

Решение. В данной задаче поле так же является одномерным. Поэтому электрический потенциал в первом слое диэлектрика (R₁?r?R₂) удовлетворяет уравнению (1.26), а во втором слое (R₂?r?R₃) – уравнению (1.27). Эти уравнения имеют решения (1.28) и (1.30), соответственно. Перепишем их (при n=2) в следующем виде:

Для определения постоянных интегрирования С₁, С₂, С₃, С₄ поставим граничные условия.

Так, если принять потенциал наружного электрода равным нулю, то потенциал внутреннего электрода будет равен U₀.

; (1.44)

.

На границе раздела слоев диэлектриков (r=R₂) равны между собой потенциалы и векторы электрического смещения (вектор электрического смещения имеет одну составляющую, направленную вдоль радиуса).

Решая систему уравнений, составленную из последних двух уравнений и уравнений (1.44) и (1.45) относительно постоянных интегрирования, получаем С₁=-94.917, С₂=-555.628, С₃=-48.588, С₄=-268.279.

Таким образом, выражения для напряженности электрического поля и потенциала принимают вид

Графики изменения данных функций вдоль радиуса представлены на рис. 1.30.

Все значения на графике даны в относительных единицах. За базисное значение напряженности поля и потенциала приняты их значения на поверхности внутреннего электрода E_b=95.06кВ/м,

U_b=100В. За базисное значение радиальной координаты принят внутренний радиус наружного электрода R₂.

Пример 4. Две протяженные проводящие пластины расположены в воздухе под углом a₀=p/4 друг к другу и не соприкасаются (рис. 1.31). Напряжение между пластинами U₀=100В.

Пренебрегая краевым эффектом, определить закон распределения потенциала и напряженности электрического поля между пластинами.

Поле между пластинами является одномерным (все величины зависят только от одной угловой координаты a цилиндрической системы координат). Потенциал, в этом случае, удовлетворяет уравнению (1.32) с решением (1.34).

Постоянные интегрирования определяются из граничных условий

Из данной системы уравнений определяем постоянные интегрирования С₂=0, С₁=U₀/a₀.

Таким образом, закон изменения искомых функций вдоль угловой координаты a цилиндрической системы координат можно окончательно представить следующим образом:

Как видно из последних выражений, эквипотенциальными поверхностями являются полуплоскости, проходящие через ось OZ и изолированными драг от друга, а линиями поля являются дуги окружностей с центром в начале координат.

Пример 5. Шар из диэлектрика (e_r = 4) заряжен и расположен в воздухе. Объемная плотность заряда является функцией расстояния r от центра шара: r = k*r (k = 0,05p). Радиус шара R = 2см.

Рассчитать потенциал и напряженность электрического поля внутри и вне шара.

Данная задача была решена в примере 3 раздела 1.14 с помощью теоремы Гаусса.

Покажем, что этой же цели можно добиться и путем решения уравнений Пуассона (1.35) и Лапласа (1.36), которым удовлетворяет потенциал поля внутри и вне шара, соответственно.

Выражения, определяющие этот потенциал внутри (1.37) и вне шара (1.39), можно для данного случая представить в следующем виде:

Постоянные интегрирования определяются из известных граничных условий и с помощью некоторых физических соображений. Так, потенциал в центре шара (r=0) имеет конечное значение, поэтому постоянную С₁ необходимо принимать равной нулю (С₁=0). Далее, принимая потенциал равный нулю в точке, лежащей в бесконечности (r=?), получаем С₄=0.

Оставшиеся две постоянные С₂ и С₃ определяем исходя из того, что на поверхности шара (r=R) равны между собой потенциалы и нормальные составляющие вектора электрического смещения

Перепишем данные граничные условия в следующем виде:

Решая совместно последние уравнения, находим постоянные интегрирования. C₂=38460, С₃=-709,964.

Подставляя значения этих постоянных в формулы для потенциалов, получаем

Отсюда видно, что данные выражения полностью аналогичны тем, которые были получены в примере 3 предыдущего раздела.

Пример 6. Две тонкие проводящие поверхности в виде коаксиальных конусов с изолированными вершинами расположены в воздухе. Потенциал первой поверхности U₁=0, второй – U₂=100В (рис. 1.32), q₁=p/6, q₂=2p/3.

Найти закон распределения потенциалов и напряженности электрического поля в пространстве между конусами.

Данная задача является одномерной, поскольку, в силу симметрии, решение для потенциала U зависит только от угла q. Поле в данном случае характеризуется уравнением (1.40) и имеет решение (1.41).

Исходя из заданных граничных условий составим уравнения для нахождения постоянных интегрирования С₁ и С₂

Решая данную систему, получим С₁=53.583, С₂=70.567.

Таким образом, выражение для определения потенциала будет иметь вид

Напряженность электрического поля имеет одну составляющую

Эквипотенциальными поверхностями являются поверхности конусов с изолированными вершинами. При q=p/2 один из конусов переходит в плоскость. Линии поля лежат на меридианах.

Уравнение пуассона для электростатического поля в диэлектрике

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКЕ

§1 Проводники и диэлектрики. Полярные и неполярные молекулы. Ионные кристаллы. Свободные и связанные заряды. Типы поляризации.

• Проводники и диэлектрики смотри Лекци. 1 по Электростатике.
• Типы диэлектриков.

Молекула диэлектрика, как и молекула любого другого вещества, электрически нейтральна. Это означает, что суммарный отрицательный заряд электронов равен суммарному положительному заряду ядер.

Если у молекулы в отсутствие внешнего электрического поля центры тяжести положительного и отрицательного зарядов совпадают, то есть дипольный момент молекулы , то такие молекулы называются неполярными. К ним относятся молекулы H ₂ , O ₂ , N ₂ .

Молекулы, у которых в отсутствие внешнего поля центры тяжести положительных и отрицательных зарядов не совпадают, то есть существует дипольный момент , называются полярными. К ним относятся H ₂ O , CO , NH , HCl , SO ₄ , и др.

Ионные кристаллы ( NaCl , KBr , KCl ) имеют кристаллическое строение. В узлах пространственной решетки расположены с чередованием ионы разных знаков. В ионных кристаллах нельзя выделить отдельные молекулы. Их нужно рассматривать как систему двух подрешеток – положительной и отрицательной.

Кристаллическая решетка поваренной соли

ПОЛЯРИЗАЦИЕЙ диэлектрика называется процесс ориентации диполей или появление под воздействием электрического поля ориентированных по полю диполей.

(Возникновение дипольного момента в диэлектрике называется ПОЛЯРИЗАЦИЕЙ)

В результате поляризации молекула приобретает дипольный момент , величина которого пропорциональна полю

где α – поляризуемость молекулы (характеризует «реакцию» молекулы на электрическое поле). Α – характеристика атома или иона.

В качестве величины, характеризующей степень поляризации диэлектрика, принимается вектор ПОЛЯРИЗОВАННОСТИ — дипольный момент единицы объема (или плотность дипольного момента)

где — дипольный момент одной молекулы, — суммарный дипольный момент объема V .

Трём типам диэлектриков соответствуют три типа поляризации

• ЭЛЕКТРОННАЯ ПОЛЯРИЗАЦИЯ – возникновение дипольного момента в неполярных молекулах. Электронная поляризация обусловлена смещением электронной оболочки атома относительно ядра во внешнем поле.

ИОННАЯ ПОЛЯРИЗАЦИЯ – возникновение дипольного момента в ионных кристаллах, вызванное смещением подрешеток положительных ионов вдоль поля, а отрицательных – против поля.

• ОРИЕНТАЦИОННАЯ (ДИПОЛЬНАЯ) ПОЛЯРИЗАЦИЯ – возникновение дипольного момента в диэлектрике с полярными молекулами вследствие ориентации дипольных моментов молекул по направлению поля.

• СВОБОДНЫЕ И СВЯЗАННЫЕ ЗАРЯДЫ

Заряды, которые при приложении внешнего электрического поля могут свободно перемещаться по проводнику, и не связаны с ионами кристаллической решетки, называются свободными.

Заряды, входящие в состав молекулы, которые под действием внешнего поля лишь немного смещаются из своих положений равновесия, и покинуть пределы молекулы не могут, называются связанными.

§2 Напряженность поля в диэлектрике.

У изотропных диэлектриков вектор поляризации линейно зависит от напряженности поля

где χ – ДИЭЛЕКТРИЧЕСКАЯ ВОСПРИМЧИВОСТЬ вещества, показывает, как диэлектрик реагирует (воспринимает) на внешнее электрическое поле.

α – характреистика отдельной молекулы (иона), χ – характеристика всего диэлектрика, то есть характреистика вещества в целом. χ не зависит от и в слабых полях. χ – безразмерная величина

Если между пластинами плоского конденсатора поместить слой диэлектрика, то в результате поляризации положительные заряды в диэлектрике сместятся по полю, а отрицательные – против поля, и на правой грани (по рисунку) возникнет избыток положительных, а на левой гране – избыток отрицательных зарядов с поверхностной плотностью +σ’ и –σ’. Эти заряды создадут внутри диэлектрической пластины однородное поле, напряженность которого по теореме Гаусса равна

где — поверхностная плотность связанных зарядов.

Вне диэлектрика . Внешнее поле и внутренн направлены навстречу друг другу, следовательно, внутри диэлектрика

Вне диэлектрика .

Определим поверхностную плотность связанных зарядов . Полный дипольный момент пластинки диэлектрика

где S – площадь грани пластинки, d – её толщина. С другой стороны, полный дипольный момент равен

где Q ’ – связанный заряд каждой грани, d — плечо диполя.

или

Поверхностная плотность связанных зарядов равна поляризованности (поляризации) Р.

Тогда поле внутри диэлектрика

Безразмерная величина называется ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТЬЮ среды. Ε показывает во сколько раз поле ослабляется диэлектриком, характеризуя количественно свойство диэлектрика поляризоваться в электрическом поле.

§3 Электрическое смещение.

Теорема Гаусса для электростатического поля в диэлектрике.

Для описания электрического поля, в частности, в диэлектрике, вводят в рассмотрение вектор электрического смещения (вектор электростатической индукции) , равный

Результирующее поле в диэлектрике описывается вектором напряженности . зависит от свойств диэлектрика (от ε). Вектором описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, возникающие в диэлектрике, могут вызвать перераспределение свободных зарядов, создающих поле. Поэтому вектор характеризует электростатическое поле, создаваемое свободными зарядами (т.е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.

Силовые линии вектора могут начинаться и заканчиваться как на свободных, так и на связанных зарядах. Силовые линии вектора — только на свободных. Через области поля, где находятся связанные заряды, силовые линии вектора проходят не прерываясь.

ПОТОК ВЕКТОРА через произвольную замкнутую поверхность

ТЕОРЕМА ГАУССА ДЛЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ В ДИЭЛЕКТРИКЕ:

Поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов:

Уравнение Пуассона и математическая постановка задач электростатики

Существует большое количество случаев, когда самым удобным методом нахождения напряженности поля считается решение дифференциального уравнения для потенциала. После его получения применим в качестве основы теорему Остроградского-Гаусса в дифференциальной форме:

где ρ является плотностью распределения заряда, ε 0 — электрической постоянной, d i v E → = ∇ → E → = ∂ E x ∂ x + ∂ E y ∂ y + ∂ E z ∂ z — дивергенцией вектора напряженности и выражением, связывающим напряженность поля и потенциал.

Произведем подстановку ( 2 ) в ( 1 ) :

Учитывая, что d i v g r a d φ = ∇ 2 φ = ∂ 2 φ ∂ x 2 + ∂ 2 φ ∂ y 2 + ∂ 2 φ ∂ z 2 , где ∆ = ∇ 2 — это оператор Лапласа, равенство ( 3 ) принимает вид:

Выражение ( 4 ) получило название уравнения Пуассона для вакуума. При отсутствующих зарядах запишется как уравнение Лапласа:

После нахождения потенциала переходим к вычислению напряженности, используя ( 2 ) . Решения уравнения Пуассона должны удовлетворять требованиям:

• значение потенциала как непрерывная функция;
• потенциал должен быть конечной функцией;
• производные потенциала как функции по координатам должны быть конечными.

При наличии сосредоточенных зарядов в объеме V , решение уравнения ( 4 ) будет выражаться для потенциала вида:

Общая задача электростатики сводится к нахождению решения дифференциального уравнения, то есть уравнения Пуассона, удовлетворяющего вышеперечисленным требованиям. Теоретические вычисления известны для небольшого количества частных случаев. Если возможно подобрать функцию φ , удовлетворяющую условиям, то она является единственным решением.

В таких задачах не всегда необходимо задавать заряды или потенциалы во всем пространстве. Для нахождения электрического поля в полости, окруженной проводящей оболочкой, достаточно вычислить поле тел, находящихся внутри нее.

Любое решение уравнения Пуассона ограниченной области может быть определено краевыми условиями, накладывающимися на поведение решения. Границы перехода из одной среды в другую имеют условия, которые должны быть выполнены:

E 2 n — E 1 n = 4 π σ , или ∂ φ 1 ∂ n — ∂ φ 2 ∂ n = 0 .

где σ — это поверхностная полость свободных зарядов, n – единичный вектор нормали к границе раздела, проведенный из среды 1 в 2 , τ — единичный вектор, касательный к границе.

Эти уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной вектора напряженностей электрического поля при переходе через любую заряженную поверхность независимо от ее формы и наличия или отсутствия зарядов вне ее.

Уравнение Пуассона в сферических, полярных и цилиндрических координатах

Запись уравнения может быть как при помощи декартовых координат, также и сферических, цилиндрических, полярных.

При наличии сферических r , θ , υ уравнение Пуассона запишется как:

1 r 2 · ∂ ∂ r r 2 ∂ φ ∂ r + 1 r 2 sin θ ∂ θ sin θ · ∂ φ ∂ θ + ∂ 2 φ r 2 sin 2 θ ∂ φ 2 = — 1 ε 0 ρ .

В полярных r , θ :

1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ r 2 ∂ θ 2 = — 1 ε 0 ρ .

В цилиндрических r , υ , z :

1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ ∂ z 2 + ∂ 2 φ r 2 ∂ υ 2 = — 1 ε 0 ρ .

Примеры решения задач

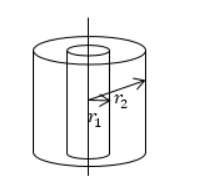
Найти поле между коаксиальными цилиндрами с радиусами r 1 и r 2 и с имеющейся разностью потенциалов ∆ U = φ 1 — φ 2 .

Решение

Необходимо зафиксировать уравнение Лапласа с цилиндрическими координатами, учитывая аксиальную симметрию:

1 r · ∂ ∂ r r ∂ φ ∂ r = 0 .

Решение имеет вид φ = — A ln ( r ) + B . Для этого следует выбрать нулевой потенциал на нужном цилиндре, тогда:

φ ( r 2 ) = 0 = — A ln r 2 + B , следовательно

φ ( r 1 ) = ∆ U = — A ln r 1 + B , получим:

A = ∆ U ln r 2 r 1 .

φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .

Ответ: поле с двумя коаксиальными цилиндрами может быть задано при помощи функции φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .

Найти потенциал поля, которое создает бесконечно круглый цилиндр с радиусом R и объемной плотностью заряда ρ . Использовать уравнение Пуассона.

Решение

Необходимо направить ось Z по оси цилиндра. Видно, что цилиндрическое распределение заряда аксиально симметрично, потенциал имеет такую же симметрию, иначе говоря, считается функцией φ ( r ) с r , являющимся расстоянием от оси цилиндра. Для решения используется цилиндрическая система координат. Уравнение Пуассона в ней запишется как:

φ 2 = C 2 ln r + C ‘ 2 .

C 1 , C ‘ 1 , C 2 , C ‘ 2 — это постоянные интегрирования. Имеем, что потенциал во всех точках должен быть конечным, а l i m r → 0 ln r = ∞ . Отсюда следует, что C 1 = 0 . Далее необходимо пронормировать потенциал, задействовав условие φ 1 ( 0 ) = 0 . Получим C ‘ 1 = 0 .

Поверхностные заряды отсутствуют, поэтому напряженность электрического поля на поверхности шара является непрерывной. Следовательно, что и производная от потенциала также непрерывна при r = R , как и сам потенциал. Исходя из условий, можно найти C 2 , C ‘ 2 :

C 2 ln R + C ‘ 2 = — 1 4 ρ ε 0 R 2 .

C 2 R = — 1 2 ρ ε 0 R .

Значит, полученные выражения записываются как:

Ответ: потенциал поля равняется: