Уравнение пуассона для вектора напряженности магнитного поля

Уравнение Пуассона и математическая постановка задач электростатики

Существует большое количество случаев, когда самым удобным методом нахождения напряженности поля считается решение дифференциального уравнения для потенциала. После его получения применим в качестве основы теорему Остроградского-Гаусса в дифференциальной форме:

где ρ является плотностью распределения заряда, ε 0 — электрической постоянной, d i v E → = ∇ → E → = ∂ E x ∂ x + ∂ E y ∂ y + ∂ E z ∂ z — дивергенцией вектора напряженности и выражением, связывающим напряженность поля и потенциал.

Произведем подстановку ( 2 ) в ( 1 ) :

Учитывая, что d i v g r a d φ = ∇ 2 φ = ∂ 2 φ ∂ x 2 + ∂ 2 φ ∂ y 2 + ∂ 2 φ ∂ z 2 , где ∆ = ∇ 2 — это оператор Лапласа, равенство ( 3 ) принимает вид:

Выражение ( 4 ) получило название уравнения Пуассона для вакуума. При отсутствующих зарядах запишется как уравнение Лапласа:

После нахождения потенциала переходим к вычислению напряженности, используя ( 2 ) . Решения уравнения Пуассона должны удовлетворять требованиям:

• значение потенциала как непрерывная функция;
• потенциал должен быть конечной функцией;
• производные потенциала как функции по координатам должны быть конечными.

При наличии сосредоточенных зарядов в объеме V , решение уравнения ( 4 ) будет выражаться для потенциала вида:

Общая задача электростатики сводится к нахождению решения дифференциального уравнения, то есть уравнения Пуассона, удовлетворяющего вышеперечисленным требованиям. Теоретические вычисления известны для небольшого количества частных случаев. Если возможно подобрать функцию φ , удовлетворяющую условиям, то она является единственным решением.

В таких задачах не всегда необходимо задавать заряды или потенциалы во всем пространстве. Для нахождения электрического поля в полости, окруженной проводящей оболочкой, достаточно вычислить поле тел, находящихся внутри нее.

Любое решение уравнения Пуассона ограниченной области может быть определено краевыми условиями, накладывающимися на поведение решения. Границы перехода из одной среды в другую имеют условия, которые должны быть выполнены:

E 2 n — E 1 n = 4 π σ , или ∂ φ 1 ∂ n — ∂ φ 2 ∂ n = 0 .

где σ — это поверхностная полость свободных зарядов, n – единичный вектор нормали к границе раздела, проведенный из среды 1 в 2 , τ — единичный вектор, касательный к границе.

Эти уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной вектора напряженностей электрического поля при переходе через любую заряженную поверхность независимо от ее формы и наличия или отсутствия зарядов вне ее.

Уравнение Пуассона в сферических, полярных и цилиндрических координатах

Запись уравнения может быть как при помощи декартовых координат, также и сферических, цилиндрических, полярных.

При наличии сферических r , θ , υ уравнение Пуассона запишется как:

1 r 2 · ∂ ∂ r r 2 ∂ φ ∂ r + 1 r 2 sin θ ∂ θ sin θ · ∂ φ ∂ θ + ∂ 2 φ r 2 sin 2 θ ∂ φ 2 = — 1 ε 0 ρ .

В полярных r , θ :

1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ r 2 ∂ θ 2 = — 1 ε 0 ρ .

В цилиндрических r , υ , z :

1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ ∂ z 2 + ∂ 2 φ r 2 ∂ υ 2 = — 1 ε 0 ρ .

Примеры решения задач

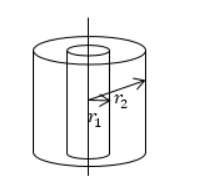
Найти поле между коаксиальными цилиндрами с радиусами r 1 и r 2 и с имеющейся разностью потенциалов ∆ U = φ 1 — φ 2 .

Решение

Необходимо зафиксировать уравнение Лапласа с цилиндрическими координатами, учитывая аксиальную симметрию:

1 r · ∂ ∂ r r ∂ φ ∂ r = 0 .

Решение имеет вид φ = — A ln ( r ) + B . Для этого следует выбрать нулевой потенциал на нужном цилиндре, тогда:

φ ( r 2 ) = 0 = — A ln r 2 + B , следовательно

φ ( r 1 ) = ∆ U = — A ln r 1 + B , получим:

A = ∆ U ln r 2 r 1 .

φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .

Ответ: поле с двумя коаксиальными цилиндрами может быть задано при помощи функции φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .

Найти потенциал поля, которое создает бесконечно круглый цилиндр с радиусом R и объемной плотностью заряда ρ . Использовать уравнение Пуассона.

Решение

Необходимо направить ось Z по оси цилиндра. Видно, что цилиндрическое распределение заряда аксиально симметрично, потенциал имеет такую же симметрию, иначе говоря, считается функцией φ ( r ) с r , являющимся расстоянием от оси цилиндра. Для решения используется цилиндрическая система координат. Уравнение Пуассона в ней запишется как:

φ 2 = C 2 ln r + C ‘ 2 .

C 1 , C ‘ 1 , C 2 , C ‘ 2 — это постоянные интегрирования. Имеем, что потенциал во всех точках должен быть конечным, а l i m r → 0 ln r = ∞ . Отсюда следует, что C 1 = 0 . Далее необходимо пронормировать потенциал, задействовав условие φ 1 ( 0 ) = 0 . Получим C ‘ 1 = 0 .

Поверхностные заряды отсутствуют, поэтому напряженность электрического поля на поверхности шара является непрерывной. Следовательно, что и производная от потенциала также непрерывна при r = R , как и сам потенциал. Исходя из условий, можно найти C 2 , C ‘ 2 :

C 2 ln R + C ‘ 2 = — 1 4 ρ ε 0 R 2 .

C 2 R = — 1 2 ρ ε 0 R .

Значит, полученные выражения записываются как:

Ответ: потенциал поля равняется:

Уравнение Пуассона и Лапласа

В случае потенциального поля напряженность поля Е может быть выражена через градиент потенциала. При этом приходим к выражению

содержащему двойную дифференциальную операцию: дивергенцию от градиента. При использовании декартовой системы координат легко записать эту операцию через соответствующие производные. Действительно, представляя в формулу (1) составляющие grad φ как:

Операция div grad носит название лапласиана и обозначается знаком Δ. Используя оператор набла, рассматриваемую операцию можно представить как наблу квадрат, таким образом:

В случае декартовых координат и в применении к скалярной функции можно всегда считать операции ∇ 2 и Δ тождественными.

Уравнение (1) является основным уравнением потенциального электрического поля и носит название уравнения Пуассона.

В области поля, где заряды отсутствуют (где ρ = 0), уравнение (1) упрощается, так как в его правой части оказывается нуль. В последнем случае уравнение называют уравнением Лапласа.

и было названо дифференциальным уравнением электрического потенциального поля.

Рассмотрим несколько примеров.

Пример 1

В некоторой области поля потенциал изменяется по закону:

Содержится ли в этой области объемный заряд и чему он равен?

Решение

Путем прямого дифференцирования найдем:

Уравнение Лапласа удовлетворяется (объемный заряд равен нулю).

Пример 2

То же, что и в предыдущем примере, но описанное следующим уравнением:

Решение

Очевидно, что правая часть данного равенства в общем случае не равна нулю.

Примечание к примерам 1 и 2. Из рассмотрения встретившихся видов произведений можно сделать более общий вывод:

всегда удовлетворяет уравнению Лапласа (первый множитель в формуле (5) cos или sin, а второй ch или sh).

Электронная библиотека

Магнитным полем называют одну из двух сторон электромагнитного поля, обусловленную движущимися заряженными частицами и изменением электрического поля, оказывающую силовое воздействие на движущиеся заряженные частицы и выявляемую по силовому воздействию, направленному нормально к направлению движения этих частиц и пропорциональному их скорости.

Основной физической величиной, характеризующей магнитное поле, является магнитная индукция .

Магнитная индукция величина векторная. Единицей измерения магнитной индукции является тесла (Тл).

Численно магнитную индукцию можно определить по механической силе f₂, действующей на один заряд q, движущийся со скоростью V:

где – векторное произведение векторов скорости и магнитной индукции.

Если выбрать такое направление скорости , чтобы оно было перпендикулярно вектору магнитной индукции , то величина силы f₂ будет наибольшей (f_2max) и

Принято также магнитную индукцию определять по силовому воздействию на отрезок проводника длиной l, по которому протекает постоянный электрический ток I. Так, если проводник поместить в магнитное поле таким образом, чтобы он был перпендикулярен вектору магнитной индукции , то

Магнитное поле, кроме магнитной индукции, характеризуется также намагниченностью вещества и напряженностью магнитного поля . Эти величины связаны следующим соотношением:

Здесь m₀ – магнитная постоянная; m_r – относительная магнитная проницаемость; m_а и m – абсолютная магнитная проницаемость.

Единицей магнитной постоянной является генри на метр (Гн/м). Магнитная постоянная m₀ имеет значение, равное 4p×10 -7 Гн/м.

Единицей напряженности магнитного поля является ампер на метр (А/м).

Для изотропного вещества

где c – магнитная восприимчивость.

В частном случае для пустоты и

Поток вектора магнитной индукции сквозь некоторую поверхность s называют кратко магнитным потоком сквозь эту поверхность и обозначают через Ф:

Магнитный поток измеряется в веберах (Вб).

Магнитный поток сквозь любую замкнутую поверхность s равен нулю (принцип непрерывности магнитного потока):

В дифференциальной форме принцип непрерывности магнитного потока имеет следующий вид:

При анализе магнитных полей важное значение имеет закон полного тока, который в интегральной форме имеет вид:

Закон полного тока гласит о том, что линейный интеграл по замкнутому контуру l от напряженности магнитного поля равен полному току, протекающему сквозь сечение, ограниченное этим контуром.

Под полным током понимают алгебраическую сумму токов проводимости, переноса и смещения.

В дифференциальной форме закон полного тока можно записать следующим образом:

В той части пространства, где плотность тока d равна нулю (правая часть уравнения (3.3) равна нулю), магнитное поле можно рассматривать как потенциальное и напряженность магнитного поля можно представить в виде

где U_м – скалярный потенциал магнитного поля.

В областях, не занятых током (только для этих областей имеет смысл функция U_м), при постоянном значении магнитной проницаемости (m = const) скалярный потенциал магнитного поля подчиняется уравнению Лапласа:

что вытекает из уравнений (3.1) и (3.4).

Линейный интеграл от напряженности магнитного поля по замкнутому контуру l, не охватывающему контура с током, равен нулю (закон полного тока). Поэтому (как в электростатическом поле), если условно принять равным нулю потенциал в некоторой точке Р (U_мр = 0), то разность потенциалов в точках А и Р будет равна потенциалу точки А:

Однако если выбрать такой путь интегрирования, который охватывает контур с током, правая часть уравнения (3.2) не будет равна нулю. Поэтому скалярный потенциал магнитного поля является функцией не однозначной, но эта не однозначность не оказывает влияния на расчет напряженности поля (i = const).

Разность магнитных потенциалов между двумя точками называют падением магнитного напряжения между этими точками.

В той части пространства, где плотность тока d не равна нулю (правая часть уравнения (3.3) не равна нулю), магнитное поле можно рассматривать как вихревое. В этом случае вектор магнитной индукции можно представить в виде вихря некоторого вспомогательного вектора :

Вектор носит название векторного потенциала магнитного поля.

Единицей измерения для векторного потенциала является Вб/м.

Основанием для представления индукции в виде (3.5) служит то, что при этом всегда соблюдается закон непрерывности магнитного потока (3.1).

В однородной среде (m = const) для векторного потенциала справедливо уравнение Пуассона

и, в частности (при d = 0), уравнение Лапласа

Общее решение уравнения (3.6) может быть представлено в следующем виде:

Интегрирование достаточно распространить по всему объему, где плотность тока Величина r – это расстояние от центра элемента объема dv, в котором плотность тока равна , до точки, в которой определяется .

Данное выражение, служащее для определения вектора по заданному распределению тока в пространстве, справедливо всюду, в частности, и там, где

Выражение (3.8) может быть упрощено, если токи протекают по контурам из линейных проводников, поперечные размеры сечений которых весьма малы по сравнению с длиной контуров и по сравнению с расстоянием от проводников до точек, в которых определяется . В этом случае формулу (3.8) можно преобразовать к следующему виду:

где l – длина контура; i – ток в контуре.

Установим связь между магнитным потоком Ф сквозь некоторую поверхность s и векторным потенциалом магнитного поля. Имеем:

Согласно теореме Стокса, последнее выражение можно переписать в виде:

Таким образом, магнитный поток сквозь поверхность s равен линейному интегралу векторного потенциала по замкнутому контуру, ограничивающему эту поверхность.

На поверхности раздела двух сред с различными магнитными проницаемостями (рис. 3.1) равны между собой касательные составляющие магнитного поля

и нормальные составляющие магнитной индукции

Здесь индекс 1 относится к первой среде, а индекс 2 – ко второй.

Условия (3.10) и (3.11) можно представить и в таком виде

Рис. 3.1. Поверхность раздела двух сред

Из данных граничных условий можно получить еще одно условие – условие преломления линий поля при переходе их из одной среды в другую:

где q₁ и q₂ – углы между вектором магнитной индукции (или напряженности) и нормалями к границе раздела сред.

При этом, если вектор напряженности перпендикулярен к границе раздела, то магнитная индукция не меняется при переходе из одной среды в другую, а напряженность поля меняется скачком.

Для расчета магнитных полей в неферромагнитных средах, ограниченных какой-либо ферромагнитной поверхностью правильной формы или в которых есть геометрически правильной формы граница между двумя средами с различными магнитными проницаемостями, широко применяют метод зеркальных изображений.

Рис. 3.2. Поле прямолинейного провода с током расположенным на расстоянии от ферромагнитной поверхности

Это искусственный прием расчета, в котором кроме заданных проводников с токами вводят еще дополнительные проводники, которые помещают там, где находятся зеркальные (в геометрическом смысле) отображения заданных проводников.

Рассмотрим поле прямолинейного провода с током I, расположенным на расстоянии h от плоской ферромагнитной поверхности (рис. 3.2).

Устраним мысленно ферромагнитную среду и заменим ее проводом, являющимся зеркальным изображением реального провода в поверхности раздела и имеющим ток такого же направления и такой же величины, как и ток реального провода (см.

рис. 3.2). Действительный провод и его зеркальное изображение составляют двухпроводную линию. Поле от такой системы проводников с токами в области над проводящей средой останется таким же, как и в действительных условиях. В этом и заключается метод зеркальных изображений.

Этот метод применим и при любом числе проводов, протянутых параллельно друг другу и параллельно плоской поверхности, ограничивающей ферромагнитную среду. Каждый провод должен быть зеркально отображен в поверхности ферромагнитной среды (направление тока остается неизменным), после чего ферромагнитная среда может быть мысленно удалена и рассмотрено поле совокупности действительных проводов и их зеркальных изображений.

При анализе электрических и магнитных полей вводят понятие о потокосцеплении y. В простейшем случае одного контура с током I магнитный поток, сцепляющийся с этим контуром, определяется этим током. Такой поток называют потоком самоиндукции. Потокосцепление самоиндукции данного контура обозначают y_L:

Коэффициент пропорциональности L называют собственной индуктивностью контура. Единицей измерения индуктивности является генри (Гн).

Собственная индуктивность всегда положительна.

Если магнитный поток, сцепляющийся с рассматриваемым контуром (например, первым), создается током I₂ во втором контуре, то для линейной среды потокосцепление будет пропорционально току I₂. При этом потокосцепление называют потокосцеплением взаимной индукции и обозначают y₁₂ или y_1М:

Величину М₁₂ называют взаимной индуктивностью контуров.

Магнитные потоки, создаваемые постоянными токами, определяют статические индуктивности, которые зависят от геометрических размеров контуров, их взаимного расположения, магнитной проницаемости контуров и среды.

Потокосцепление катушки, содержащей N витков (при условии, что магнитный поток сцепляется со всеми витками), можно определить и так:

Если магнитное поле создается токами, протекающими в n контурах, которые расположены в среде с m = const, то потокосцепление y_k с k-м контуром рассчитывается как сумма потокосцепления самоиндукции, определяемого током I_k в этом же контуре, и потокосцеплений взаимной индукции, определяемых токами в остальных контурах:

Энергия магнитного поля распределяется во всем объеме поля. При этом каждая точка поля характеризуется объемной плотностью энергии магнитного поля

Энергия магнитного поля в некотором объеме V (с учетом выражения (3.13)) равна:

Энергия магнитного поля системы n контуров с токами равна полусумме произведений токов в контурах на потокосцепление контуров:

Так, энергия магнитного поля одного контура или катушки с током определяется (с учетом выражения (3.12)) следующим образом:

Рис. 3.3. Длинный полый биметаллический провод

Энергия системы двух контуров, связанных друг с другом посредством магнитного поля, равна:

Рассмотрим несколько примеров по расчету магнитного поля.

Пример 3.1. По длинному полому биметаллическому проводу, расположенному в воздухе, проте­кает постоянный ток I = 200 А (рис. 3.3). Радиусы отверстия, внутрен­него и наружного провода равны соответственно r₀ = 4 мм, r₁ = 8 мм и r₂ = 16 мм. Внутренний провод выполнен из меди (g₁ = 58 мкСм/м), наружный – из алюминия (g₂ = 34 мкСм/м).

Определить закон изменения векторного потенциала и магнитной индукции внутри и вне провода. Построить графики изменения этих величин вдоль радиуса. Найти индуктивность провода на единицу длины.

Решение. Поскольку поле в данном случае обладает цилиндрической симметрией, то данную задачу можно решить с помощью закона полного тока, представленного в интегральной форме (3.2). Для этого разобьем область исследования на четыре подобласти. В первой подобласти (0 £ r £ r₀) напряженность магнитного поля равна нулю. Для определения напряженности поля во второй подобласти (r₀ £ r £ r₁) проводим окружность произвольным радиусом r с центром на оси провода и для контура, образованного данной окружностью, применяем закон полного тока. С учетом того, что вектор напряженности направлен по касательной к окружности и по величине остается неизменным, выражение (3.2) можно представить в следующем виде:

Аналогично определяется напряженность поля в третьей подобласти (r₁ £ r £ r₂):

Таким образом, для определения напряженности поля в соответствующих подобластях необходимо рассчитать плотность тока d₁ и d₂:

После подстановки в последние выражения соответствующих величин, получаем d₁ = 396.5 кА/м 2 , d₂ = 232.4 кА/м 2 .

Напряженность поля в четвертой подобласти (r₂ £ r £ ¥) определяется с помощь следующего выражения:

Изменение напряженности вдоль радиуса показано на рис. 3.4.

Отметим, что поскольку магнитная проницаемость во всей области одна и та же, то распределение магнитной индукции вдоль радиуса полностью повторяет распределение напряженности поля.

Рис. 3.4. Изменение напряженности вдоль радиуса

Для нахождения векторного потенциала необходимо для каждой из подобластей записать уравнение Пуассона (3.6) или Лапласа (3.7) и провести их совместное решение. Эти уравнения удобнее записывать в цилиндрической системе координат. При этом необходимо учитывать, что в данной задаче векторный потенциал имеет только одну составляющую, направленную по оси провода (по оси z), и эта составляющая зависит только от радиуса r. Раскрывая лапласиан в указанной системе координат, будем иметь:

Интегрируя дважды по r, получаем выражения для потенциала для каждой подобласти:

Слагаемое С₁lnr должно отсутствовать, так как А не может принимать бесконечно больших значений при r = 0. Отсюда следует, что постоянная интегрирования С₁ = 0. Векторный потенциал определяется с точностью до постоянной. Примем эту постоянную, равной нулю: С₈ = 0. Для определения оставшихся шести постоянных составим с помощью граничных условий систему уравнений. Эти граничные условия определяют равенство на границе раздела двух сред касательных составляющих напряженности поля и равенство векторного потенциала.

Касательной в данной задаче является угловая составляющая напряженности поля, которая определяется с помощью выражения (3.5) следующим образом:

Таким образом, для определения постоянных интегрирования получаем систему уравнений:

Решая совместно данные уравнения, получаем: С₂ = 1.845×10 -4 ; С₃ = 3.986×10 -4 ; С₄ = 2.085×10 -4 ; С₅ = -2.612×10 -6 ; С₆ = 1.733×10 -4 ; С₇ = -4×10 -4 .

На рис. 3.5 показано распределение векторного потенциала вдоль радиуса. Данные на графике представлены в относительных единицах. За базисное значение принято значение потенциала в первой зоне: А₁ = 1.845×10 -4 Вб/м.

Рис.3.5. Распределение векторного потенциала вдоль радиуса

Для определения индуктивности провода вначале найдем магнитный поток, пронизывающий биметаллический провод на длине, равной одному метру.

Для этого воспользуемся формулой (3.9), которую, с учетом того, что векторный потенциал направлен вдоль оси провода, а в подынтегральном выражении стоит скалярное произведение двух векторов, можно преобразовать к следующему виду:

Таким образом, индуктивность (на один метр длины) биметаллического провода равна: L = Ф/I = 95.5×10 -9 Гн/м.

Пример 3.2. Рассчитать напряженность магнитного поля двухпроводной линии с током I = 2700 А, провода которой выполнены из алюминия и имеют радиус R = 28 мм. Расстояние между проводами 2d = 20 м (рис. 3.6).

Решение. Решение данной задачи можно получить либо с помощью закона полного тока, либо с использованием функции векторного магнитного потенциала. Выражение векторного потенциала внутри цилиндрического провода с током и вне его уже получено в предыдущем примере. Так, внутри провода (0 £ r £ R) оно имеет вид:

а вне провода (R £ r £¥) –

Постоянные интегрирования определяются из условий равенства на поверхности провода векторного потенциала (А₁ = А₂ при r = R) и его нормальных производных (dА₁/dr = = dА₂/dr при r = R):

Нас интересует поле только вне провода, поэтому выражение для потенциала в этой области с точностью до постоянной будет иметь вид:

Используя данную формулу, запишем выражение для определения векторного потенциала в произвольной точке М (рис. 3.6) от двух проводов

Примем значение постоянной С, равной нулю (это означает, что за точку нулевого потенциала мы приняли начало координат), и перепишем последнее выражение в прямоугольной системе координат

С помощью выражения (3.5) найдем составляющие напряженности магнитного поля

Распределение данных составляющих, а также модуля напряженности магнитного поля, который определяется по формуле

Рис. 3.6. Определение векторного потенциала в произвольной точке М

при у = 10 м показано на рис. 3.7.

Рис. 3.7. Распределение данных составляющих

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00