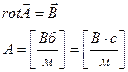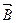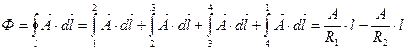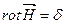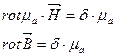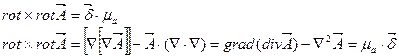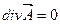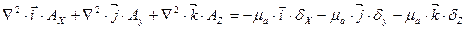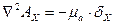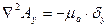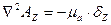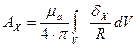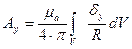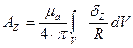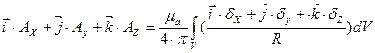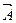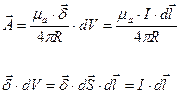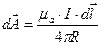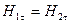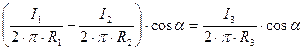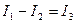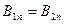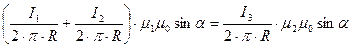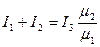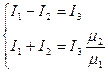Уравнение пуассона для вектора потенциала

Векторный потенциал магнитного поля

Векторный потенциал магнитного поля – это плавно меняющаяся от точки к точке векторная величина, ротор которой равен магнитной индукции.

Векторный потенциал можно применять для любых областей пространства, в том числе и для областей занятых токами.

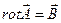
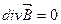
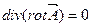
Уравнение возможно с учетом того, что (принцип непрерывности) тогда , а дивергенция от любого ротора равна нулю (из математики).

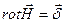
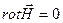
Векторный потенциал магнитного поля вводится для расчета вихревых полей ( ). Но применим и для расчета потенциальных полей .

Направление векторного магнитного потенциала такое же, как и у тока в проводнике.

С помощью векторного потенциала магнитного поля решают следующие типы задач:

1) Определение магнитной индукции

2) Определение магнитного потока, пронизывающего какой-либо контур.

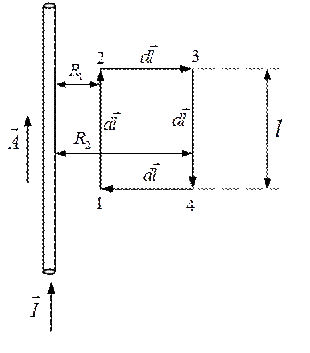
Пример: Определить поток 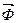, пронизывающий рамку, который создаётся проводником с током.

По теореме Стокса: заменим поверхностный интеграл на линейный (поток через поверхность ограниченную контуром заменим на циркуляцию по контуру):

Уравнение Пуассона

Для областей занятых токами

Умножим обе части уравнения на магнитную проницаемость 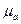=const:

Линии векторного магнитного потенциала замкнуты на себя, то есть:

Тогда 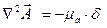-уравнение Пуассона для векторного магнитного потенциала.

Поскольку в обе части уравнения входят векторные величины, то это уравнение можно переписать для декартовой системы координат:

Решая это уравнение, получим проекции на оси координат:

умножим на единичные орты, получим:

— общее решение уравнения Пуассона.

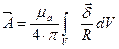
С помощью этой формулы можно найти векторный потенциал в любой точке поля, для этого интеграл в правой части уравнения должен быть взят по всем областям, занятым током.

Однако, пользоваться этой формулой каждый раз нецелесообразно, так как взятие интеграла правой части формулы сопряжено обычно со значительными математическими выкладками.

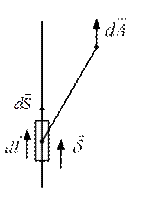
Пример: В точке А необходимо определить направление

Составляющая векторного магнитного потенциала имеет такое же направление в пространстве, как и ток в элементе проводника.

Метод зеркальных изображений

В магнитном поле постоянного тока, вблизи границы раздела двух сред, для расчета поля используют метод зеркальных изображений.

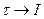
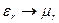
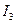
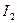
Методика расчета полностью аналогична задаче расчета электростатического поля, созданного двумя заряженными осями, расположенными вблизи плоской границы раздела двух диэлектриков с различными диэлектрическими проницаемостями.. Линейная плотность заряда заменяется током ( ), а относительная диэлектрическая постоянная среды — относительной магнитной постоянной( )

и — фиктивные токи

Найдем фиктивные токи, исходя из граничных условий. Для этого рассмотрим точку, лежащую на границе раздела сред; ее можно считать принадлежащей как к первой, так и ко второй среде.

Из первого граничного условия

Левая часть уравнения определяет принадлежность точки первой среде.

Правая часть уравнения определяет принадлежность точки второй среде.

Сокращая одинаковые элементы в правой и левой частях уравнения, получим

Из второго граничного условия

Левая часть уравнения определяет принадлежность точки к первой среде.

Правая часть уравнения определяет принадлежность точки ко второй среде.

Сокращая одинаковые элементы в правой и левой частях уравнения, получим:

Решая систему из двух уравнений, получим значения фиктивных токов:

Уравнение Пуассона для вектора-потенциала

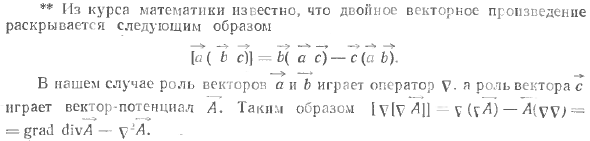
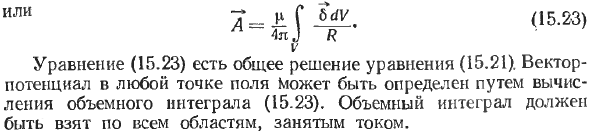
Уравнение Пуассона для вектора-потенциала

Уравнение Пуассона векторного потенциала. Умножим проницаемость среды p с обеих сторон (15.4): P rot II = pd. Согласитесь обрабатывать носители, которые можно подразделить на отдельные области, чтобы проницаемость p каждой области была постоянной.

• Если p является константой, ее можно разместить под знаком p ротора. // ‘= rot B = p (15.17) (15.17) использует rot A вместо B. ротрот A = pb. (15.18) Операция по извлечению ротора из ротора в основном представляет собой

операцию по открытию двойного векторного произведения Людмила Фирмаль

и выполняется следующим образом **: rot rot A = [V [VA] 1 = grad div A -V2 A = p 6 (15.19) ** Из курса математики известно, что произведение двойного вектора раскрывается как [a (bc)] — b (ac) -c (ab ). В этом случае роли векторов a и b играет оператор V.

Роль вектора c играет векторный потенциал A. Следовательно, IVIV ^ 11-V (? A) -A (== grad divZ-v ‘L. 4 — это вычисляемая функция, поэтому вы имеете право подчиняться требованиям поля DC divH-O (15.20)

• Не было никаких дополнительных требований к потенциальному вектору, что означает, что линия вектора A является линией, замкнутой сама по себе с учетом (15.20). Уравнение (15.19)

Следующая форма rd (15.21) (15.21) — не что иное, как уравнение Пуассона, в отличие от уравнения (13.26): оно построено относительно векторных величин, а -> — ■ «-> — * + / -J-

уравнение (13.26) построено относительно скалярных величин Людмила Фирмаль

Заменить на kA2 и заменить плотность тока q на + + v27 ^ — | -. Последнее уравнение для скалярных величин Al и A Разделенный на три составленных уравнения: *, Ar: P2L = -rbg (15.22a) (15.226) (15.22c) (15.22a) to t, (15.226) to /, (15.22c) К к

Если их добавить, их общие решения аналогичны уравнениям (13.26), уравнение (15.23) является общим решением уравнения (15.21), а векторный потенциал в любой точке поля

Может быть определен путем вычисления интеграла объема (15.23), который должен быть получен по всей площади, занимаемой током.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института