Уравнение Пуассона и математическая постановка задач электростатики
Вы будете перенаправлены на Автор24
Решение уравнения Пуассона
В достаточно большом количестве случаев наиболее удобным методом поиска напряженности поля является решение дифференциального уравнения для потенциала. Получим его, используя в качестве основы теорему Остроградского — Гаусса в дифференциальной форме:
где $\rho $ — плотность распределения заряда, $<\varepsilon >_0$ — электрическая постоянная, $div\overrightarrow
Подставим (2) в (1), получим:
Учитываем, что $divgrad\varphi =<\nabla >^2\varphi =\frac<<\partial >^2\varphi ><\partial x^2>+\frac<<\partial >^2\varphi ><\partial y^2>+\frac<<\partial >^2\varphi ><\partial z^2>$, где $\triangle =<\nabla >^2$- оператор Лапласа, тогда равенство (3) запишем как:
Уравнение (4) называется уравнением Пуассона (для вакуума) в системе СИ. Если заряды отсутствуют, то уравнение (4) преобразуется в уравнение Лапласа:
После того, как найден потенциал из уравнения Пуассона, обычно вычисляется напряженность по формуле (2). Решения уравнения Пуассона должны удовлетворять таким требованиям:
- Потенциал должен быть непрерывной функцией.
- Потенциал должен быть конечной функцией.
- Производные от потенциала как функции по координатам должны быть конечными.
Если заряды сосредоточены в объеме V, то решением уравнения (4) будет выражение для потенциала вида:
Итак, общая задача электростатики сводится к нахождению решения дифференциального уравнения (уравнения Пуассона), которое удовлетворяет выше перечисленным требованиям. Нахождение решения — задача весьма сложная. Теоретические решения известны для небольшого количества частных случаев. Если удалось подобрать функцию $\varphi $, которая удовлетворяет всем условиям задачи, то она единственная.
Готовые работы на аналогичную тему
Не всегда есть необходимости задавать заряды или потенциалы во всем пространстве. Например, если необходимо найти электрическое поле в полости, которая окружена проводящей оболочкой, то можно найти поле только для тел внутри самой полости.
Каждое решение уравнения Пуассона в ограниченной области однозначно определяется краевыми условиями, которые накладывают на поведение решения. На границе перехода из одной среды в другую выполняются граничные условия:
где $\sigma $- поверхностная плотность свободных зарядов, n- единичный вектор нормали к границе раздела, проведенный из среды 1 в 2, $\tau -\ $единичный вектор, касательный к границе.
Данные уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной составляющей вектора напряженностей электрического поля при переходе через любую заряженную поверхность не зависимо от формы этой поверхности и наличия и отсутствия зарядов вне ее.
Уравнение Пуассона в сферических, полярных и цилиндрических координатах
Уравнение Пуассона может быть записано не только в декартовых координатах, но также в сферических и цилиндрических, полярных.
В сферических координатах ($r,\theta ,\vartheta)$ уравнение Пуассона имеет следующий вид:
В полярных координатах ($r,\theta )$ система координат уравнение имеет вид:
В цилиндрических координатах ($r,\vartheta,z)$ уравнение имеет вид:
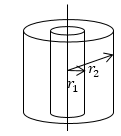
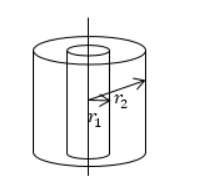
Задание: Найдите поле между двумя коаксиальными цилиндрами с радиусами $r_1$ и $r_2$, разность потенциалов между которыми равна $\triangle U=<\varphi >_1-<\varphi >_2.$
Запишем уравнение Лапласа в цилиндрических координатах с учетом аксиальной симметрии:
Оно имеет решение $\varphi =-Aln(r)$+B. Выберем нулевой потенциал на наружном цилиндре, найдем, получим:
$\varphi \left(r_2\right)=0=-Alnr_2+B,$ следовательно
Ответ: Поле между двумя коаксиальными цилиндрами задается функцией $\varphi (r)=-\frac<\triangle U><
Задание: Найти, используя уравнение Пуассона потенциал поля, которое создает бесконечно длинный круглый цилиндр радиуса R с объемной плотностью заряда $\rho $.
Ось Z направим по оси цилиндра. Так как цилиндрическое распределение заряда аксиально симметрично, то потенциал обладает той же симметрией, то есть он является функцией $\varphi \left(r\right),\ $где r — расстояние от оси цилиндра. Поэтому используем цилиндрическую систему координат. Запишем уравнение Пуассона в ней с учетом симметрии:
где $C_1$,$\
Так как поверхностных зарядов нет, то напряженность электрического поля на поверхности шара непрерывна, то есть непрерывна производная от потенциала при r=R. И непрерывен сам потенциал. Эти условия дают два алгебраических уравнения для того, чтобы найти постоянные $C_2$,$\
Следовательно, получаем выражения для потенциалов:
\[<\varphi >_1\left(r\right)=-\frac<1><4>\frac<\rho ><<\varepsilon >_0> r ^ 2 \left(0 Ответ: Потенциал поля равен: $$ \varphi_1 \left(r \right)=-\frac<1><4>\frac<\rho > <\varepsilon_0>r^2 \left (0
Уравнение Пуассона и математическая постановка задач электростатики
Существует большое количество случаев, когда самым удобным методом нахождения напряженности поля считается решение дифференциального уравнения для потенциала. После его получения применим в качестве основы теорему Остроградского-Гаусса в дифференциальной форме:
где ρ является плотностью распределения заряда, ε 0 — электрической постоянной, d i v E → = ∇ → E → = ∂ E x ∂ x + ∂ E y ∂ y + ∂ E z ∂ z — дивергенцией вектора напряженности и выражением, связывающим напряженность поля и потенциал.
Произведем подстановку ( 2 ) в ( 1 ) :
Учитывая, что d i v g r a d φ = ∇ 2 φ = ∂ 2 φ ∂ x 2 + ∂ 2 φ ∂ y 2 + ∂ 2 φ ∂ z 2 , где ∆ = ∇ 2 — это оператор Лапласа, равенство ( 3 ) принимает вид:
Выражение ( 4 ) получило название уравнения Пуассона для вакуума. При отсутствующих зарядах запишется как уравнение Лапласа:
После нахождения потенциала переходим к вычислению напряженности, используя ( 2 ) . Решения уравнения Пуассона должны удовлетворять требованиям:
- значение потенциала как непрерывная функция;
- потенциал должен быть конечной функцией;
- производные потенциала как функции по координатам должны быть конечными.
При наличии сосредоточенных зарядов в объеме V , решение уравнения ( 4 ) будет выражаться для потенциала вида:
Общая задача электростатики сводится к нахождению решения дифференциального уравнения, то есть уравнения Пуассона, удовлетворяющего вышеперечисленным требованиям. Теоретические вычисления известны для небольшого количества частных случаев. Если возможно подобрать функцию φ , удовлетворяющую условиям, то она является единственным решением.
В таких задачах не всегда необходимо задавать заряды или потенциалы во всем пространстве. Для нахождения электрического поля в полости, окруженной проводящей оболочкой, достаточно вычислить поле тел, находящихся внутри нее.
Любое решение уравнения Пуассона ограниченной области может быть определено краевыми условиями, накладывающимися на поведение решения. Границы перехода из одной среды в другую имеют условия, которые должны быть выполнены:
E 2 n — E 1 n = 4 π σ , или ∂ φ 1 ∂ n — ∂ φ 2 ∂ n = 0 .
где σ — это поверхностная полость свободных зарядов, n – единичный вектор нормали к границе раздела, проведенный из среды 1 в 2 , τ — единичный вектор, касательный к границе.
Эти уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной вектора напряженностей электрического поля при переходе через любую заряженную поверхность независимо от ее формы и наличия или отсутствия зарядов вне ее.
Уравнение Пуассона в сферических, полярных и цилиндрических координатах
Запись уравнения может быть как при помощи декартовых координат, также и сферических, цилиндрических, полярных.
При наличии сферических r , θ , υ уравнение Пуассона запишется как:
1 r 2 · ∂ ∂ r r 2 ∂ φ ∂ r + 1 r 2 sin θ ∂ θ sin θ · ∂ φ ∂ θ + ∂ 2 φ r 2 sin 2 θ ∂ φ 2 = — 1 ε 0 ρ .
В полярных r , θ :
1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ r 2 ∂ θ 2 = — 1 ε 0 ρ .
В цилиндрических r , υ , z :
1 r · ∂ ∂ r r ∂ φ ∂ r + ∂ 2 φ ∂ z 2 + ∂ 2 φ r 2 ∂ υ 2 = — 1 ε 0 ρ .
Примеры решения задач
Найти поле между коаксиальными цилиндрами с радиусами r 1 и r 2 и с имеющейся разностью потенциалов ∆ U = φ 1 — φ 2 .
Решение
Необходимо зафиксировать уравнение Лапласа с цилиндрическими координатами, учитывая аксиальную симметрию:
1 r · ∂ ∂ r r ∂ φ ∂ r = 0 .
Решение имеет вид φ = — A ln ( r ) + B . Для этого следует выбрать нулевой потенциал на нужном цилиндре, тогда:
φ ( r 2 ) = 0 = — A ln r 2 + B , следовательно
φ ( r 1 ) = ∆ U = — A ln r 1 + B , получим:
A = ∆ U ln r 2 r 1 .
φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .
Ответ: поле с двумя коаксиальными цилиндрами может быть задано при помощи функции φ ( r ) = — ∆ U ln r 2 r 1 ln ( r ) + ∆ U ln r 2 r 1 ln r 2 .
Найти потенциал поля, которое создает бесконечно круглый цилиндр с радиусом R и объемной плотностью заряда ρ . Использовать уравнение Пуассона.
Решение
Необходимо направить ось Z по оси цилиндра. Видно, что цилиндрическое распределение заряда аксиально симметрично, потенциал имеет такую же симметрию, иначе говоря, считается функцией φ ( r ) с r , являющимся расстоянием от оси цилиндра. Для решения используется цилиндрическая система координат. Уравнение Пуассона в ней запишется как:
φ 2 = C 2 ln r + C ‘ 2 .
C 1 , C ‘ 1 , C 2 , C ‘ 2 — это постоянные интегрирования. Имеем, что потенциал во всех точках должен быть конечным, а l i m r → 0 ln r = ∞ . Отсюда следует, что C 1 = 0 . Далее необходимо пронормировать потенциал, задействовав условие φ 1 ( 0 ) = 0 . Получим C ‘ 1 = 0 .
Поверхностные заряды отсутствуют, поэтому напряженность электрического поля на поверхности шара является непрерывной. Следовательно, что и производная от потенциала также непрерывна при r = R , как и сам потенциал. Исходя из условий, можно найти C 2 , C ‘ 2 :
C 2 ln R + C ‘ 2 = — 1 4 ρ ε 0 R 2 .
C 2 R = — 1 2 ρ ε 0 R .
Значит, полученные выражения записываются как:
Ответ: потенциал поля равняется:
Сравнение численного решения уравнения Пуассона в декартовой и цилиндрической системах координат Текст научной статьи по специальности « Физика»
Аннотация научной статьи по физике, автор научной работы — Чурюмов Геннадий Иванович, Старчевский Юрий Львович, Лебедев Олег Григорьевич, Новиков Николай Иванович
Рассматривается трёхмерное численное решение уравнения Пуассона конечно-разностным неявным итерационным методом в декартовой и цилиндрической системах координат. Показывается, что погрешность аппроксимации уравнения Пуассона в декартовой системе координат зависит только от величины пространственной дискретизации, а в цилиндрической системе координат эта погрешность зависит от величины пространственной дискретизации и радиуса. Для оценки влияния этих факторов на эффективность численного решения уравнения Пуассона проводится вычислительный эксперимент, который позволяет дать количественную сравнительную оценку точности и времени решения.
Похожие темы научных работ по физике , автор научной работы — Чурюмов Геннадий Иванович, Старчевский Юрий Львович, Лебедев Олег Григорьевич, Новиков Николай Иванович
The comparison of numeric solution Poisson equation in Cartesian and cylindrical coordinates systems
In this work the sharp of numeric solution Poisson equation in Cartesian and cylindrical coordinates estimates. The Three dimensional numeric solutions of potential distribution in work space of magnetron gun confirm analytic conclusions concerned to the sharp are shown. The optimization way of calculation the exist mathematics models is given.
Текст научной работы на тему «Сравнение численного решения уравнения Пуассона в декартовой и цилиндрической системах координат»
СРАВНЕНИЕ ЧИСЛЕННОГО РЕШЕНИЯ УРАВНЕНИЯ ПУАССОНА В ДЕКАРТОВОЙ И ЦИЛИНДРИЧЕСКОЙ СИСТЕМАХ КООРДИНАТ
ЧУРЮМОВ Г.И., СТАРЧЕВСКИЙЮ.Л., ЛЕБЕДЕВ О.Г., НОВИКОВ Н.И.
Рассматривается трёхмерное численное решение уравнения Пуассона конечно-разностным неявным итерационным методом в декартовой и цилиндрической системах координат. Показывается, что погрешность аппроксимации уравнения Пуассона в декартовой системе координат зависит только от величины пространственной дискретизации, а в цилиндрической системе координат эта погрешность зависит от величины пространственной дискретизации и радиуса. Для оценки влияния этих факторов на эффективность численного решения уравнения Пуассона проводится вычислительный эксперимент, который позволяет дать количественную сравнительную оценку точности и времени решения.
При проведении электродинамических расчётов численными методами важным этапом является выбор и проверка согласованности, точности, устойчивости и эффективности разностных схем аппроксимации уравнений в частных производных [1]. В практике разработки численных математических моделей используются различные схемы разностной аппроксимации. Это требует проведения подробного анализа данных моделей с точки зрения удовлетворения указанным выше критериям.
Целью данной работы является анализ точности и эффективности численного решения уравнения Пуассона в декартовой и цил индрической системах координат.
лений. Однако применение декартовой системы координат для решения задач, обладающих азимутальной симметрией, вызывает трудности, связанные с корректным заданием граничных условий. Для оценки точности вычислений рассмотрим и сравним численное решение азимутально-симметричной задачи в двух системах координат, выделяя положительные и отрицательные моменты такого решения.
Рис. 1. Выбор системы координат
В декартовой системе координат уравнение Пуассона запишется в виде:
g2U(x,y,z) f a2U(x,y,z) + ax2 ay2
| a2U(x,y,z) p(x,y,z) * (1) 2
2. Постановка задачи
Известно, что аналитические решения уравнения Пуассона существуют только для простейших случаев задания граничных условий. В действительности часто приходится сталкиваться со сложной геометрией электродов и неравномерным распределением плотности объёмного заряда р . Поэтому приходится применять численные методы решения. В этом случае выбор системы координат для решения уравнения Пуассона зависит от конфигурации электродов и исследуемого пространства (рис. 1, а и б). К тому же, конечно-разностные выражения, записанные в декартовой системе координат, обычно более простые и легче для вычис-
Решение (1) ищется при помощи разностной схемы, которая показана на рис. 2 и описана в работе [2]. Используя трёхточечную разностную аппроксимацию, уравнение (1) запишем в виде:
Ui+1,j,k 2′ Ui, j,k + Ui-1,j,k
, Ui,j+1,k _ 2′ Ui,j, k + Ui,j-1,k
‘ hy , Ui,j,k+1 _ 2 • Ui,j, k + Ui,j,k-1
Переменные i, j, k в (2) обозначают номер узла по осям x, y, z . Количество узлов по каждой оси и размеры расчётной области выбираются пользователем, и, исходя из этих данных, вычисляются
соответствующие шаги сетки hx, hy, hz .
Рис. 2. Сеточная схема в декартовой системе координат
Во всех точках сетки задаются начальные значения потенциала и плотности заряда. Окончательно
потенциал для (i, j, k) узла может быть представлен в виде:
Pi,j,k + U.+1,j,k + Ui-1,j,k
Ui,j+1,k + Ui,j-1,k + Ui,j,k+1 + Ui,j,k-1
где Є1 (h) — ошибка разностной аппроксимации уравнения Пуассона в декартовой системе координат.
Выражение (3) используется для определения потенциалов узлов в рассматриваемой области с помощью итерационного метода, который подробно описан в [2].
В цилиндрической системе координат уравнение Пуассона запишется в виде:
д 2U(r, 9,z) д 2U(r, 9,z)
+ 6U(r, 9,z) + 92U(r, 9,z) _ p(r, 9,z) (4)
Решение (4) ищется при помощи разностной схемы, которая показана на рис. 3 и описана в работе [2].
Рис. 3. Сеточная схема в цилиндрической системе координат
В этом случае (4) приближённо записывается в виде:
Ui, j,k+1 2′ Ui,j,k + Ui,j,k-1
2′ Ui,j,k + Ui —1, j,k +
2′ Ui,j,k + Ui,j—1,k _ Pi,j,k
Переменные i, j, k в (5) обозначают номер узла по осям r , ф, z . По аналогии с декартовой системой координат окончательно получаем потенциал для (i, j, k) узла:
Ui,j,k+1 + Ui,j,k-1 + Ui+1,j,k + Ui—1, j,k
Ui+1,j,k + Ui—1,j,k + Ui,j+1,k + Ui,j-1,k | Pi,j,k
. 2 + , 2 + 2^2 hx hr r • hm
где є 2(h) — ошибка разностной аппроксимации уравнения Пуассона в цилиндрической системе координат.
Выражения (3) и (6) являются базовыми для решения уравнения Пуассона в декартовой и цилиндрической системах координат. Для более точного представления границ расчётной области в декартовой системе координат использовался метод, предложенный в [3]. Он заключался в применении опорных точек в местах пересечения границ с линиями сетки для составления разностных уравнений. Для определения координат опорных точек необходимо решать систему уравнений, описывающих границы расчётной области и линии сетки. Это несколько усложняет алгоритм, однако позволяет значительно повысить точность описания границ электродов с помощью равномерной сетки разбиения. В результате имеем, что в области, прилегающей непосредственно к поверхности электродов, сетка становится неравномерной. В этом случае уравнение (1) перепишется в виде1:
U(x + hx) — U U — U(x — h x)
U(y + h+) — U U — U(y — h^)
U(z + hz) — U U — U(z — hz)
где h x,h y,hz — расстояние между соответствующими текущими и следующими узлами координат-
ной сетки; hx ,h y,hz — расстояние между соответствующими текущими и предыдущими узлами координатной сетки.
Из выражения (7) можно получить следующую итерационную формулу для общего случая неравномерной сетки:
U(x + h X) + U(x — hx) hx hx
hx ^ hx hy + hy hz ^ hz
Для сокращения записей переменные, по которым не ведётся дифференцирование, опущены.
U(y + h + ) U(y — h у)
hx + hx hy + hy hz + hz
hx + hx hy + hy hz + hz
hx hx __________т________
hx + hx hy + hy hz ^ hz
Выражение (8) позволяет при достаточном числе итераций получить численное решение уравнения Пуассона в декартовой системе координат.
3. Оценка точности разностной аппроксимации
В работе [2] при помощи разложения функции для потенциала в ряд Тейлора в окрестности точки
(i,j,k) , для которой z є [z-hz;z + hz],
r є [r-hr;r + hr], фє [ф-h9;ф + h^|, и последующей подстановки в разностные выражения показано, что трёхточечная разностная схема первой и второй производных имеет второй порядок точности.
Тогда первая и вторая производные могут быть представлены в виде суммы истинного значения и некоторой погрешности, связанной с разностной аппроксимацией.
Рассмотрим третий и четвёртый члены уравнения Пуассона (4) в цилиндрической системе координат:
С учётом сказанного выше выражения (9) запишутся в виде:
UW + OVi) и ШМ+. (10)
Первый член в каждом из выражений (10) представляет собой истинное значение соответствующего члена уравнения Пуассона, а второй характеризует вычислительную погрешность.
Уравнение Пуассона в декартовой системе координат не содержит членов, похожих на выражения (9), поэтому погрешность аппроксимации уравнения Пуассона в декартовых координатах определяется
величинами O(hx2), O(hy2), O(hz2). В цилиндрической системе координат погрешность аппроксимации уравнения Пуассона определяется величина-
Для оценки влияния выбора системы координат на точность и эффективность решения уравнения Пуассона был проведен численный эксперимент для азимутально-симметричной задачи.
4. Численный эксперимент
Численное решение уравнения Пуассона проводилось для расчёта магнетронной пушки [4], схема пространства взаимодействия которой представлена на рис. 4.
Рис. 4. Схема рабочего пространства магнетронной пушки: 1 — катод; 2 — анод; 3 — коллектор;
4 — граница расчётной области
На рис.5 показано распределение потенциала в сечении А-А в цилиндрической системе координат, а на рис. 6 — распределение потенциала в сечении А-А в декартовой системе координат. Для расчёта распределения потенциала во всём объёме, заключённом в границе расчётной области, необходим обоснованный выбор шага сетки и количества итераций, поскольку эти параметры влияют на эффективность и точность расчёта процесса формирования электронного пучка. Максимальная погрешность расчёта методом сеток находится примерно в середине межэлектродного промежутка, поскольку на электродах значения потенциала заданы абсолютно точно граничными условиями.
Для оценки величины относительной погрешности dU и сравнения решений, проведенных в цилиндрической и декартовой системах координат, был просчитан ряд тестовых задач. Результаты расчётов приведены на рис. 7 и 8.
Для сравнения был выбран потенциал, рассчитанный аналитически в сечении А-А по формуле:
‘анода у гкатода )
Рис. 5. Распределение потенциала в цилиндрической системе координат
Рис. 6. Распределение потенциала в декартовой системе координат
На рис. 7 показаны зависимости относительной погрешности 5U от числа итераций N в цилиндрической системе координат, которая определяется с учётом (11) следующим выражением:
На рис. 8 показаны зависимости относительной погрешности 5U от числа итераций N, рассчитанной по формуле (12) в декартовой системе координат.
Анализ показывает, что независимо от системы координат при уменьшении шага сетки для дости-
жения необходимой точности нужно увеличивать число итераций. При значительном увеличении числа итераций погрешность перестаёт уменьшаться и стремится к некоторому минимальному значению, которое определяется дискретностью пространственной сетки. Для дальнейшего уменьшения погрешности необходимо выбирать более мелкую сетку, а затем увеличивать число итераций.
—9—75*75*20 —в—50*50*20 —*— 35*35*20 —*— 15*15*20
Рис. 7. Зависимости максимальной относительной погрешности dU от числа итераций N в цилиндрической системе координат
Рис. 9. Время t, затрачиваемое на расчёт одной итерации, в зависимости от дискретности сетки
Для расчёта физических процессов, протекающих в азимутально-симметричных приборах, обычно используется цилиндрическая система координат. Рассмотрим возможность оптимизации расчётов, проведенных в работе [5], при помощи перехода к декартовой системе координат.
На рис. 10 показана зависимость относительной погрешности от числа итераций для двухмерных равномерных сеток 200*2 50 для цилиндрической и декартовой систем координат.
Рис. 8. Зависимости максимальной относительной погрешности dU от числа итераций N в декартовой системе координат
На рис. 9 представлена зависимость времени, затрачиваемого на расчёт одной итерации, от дискретности сетки. Время, затрачиваемое на расчёт одной итерации в цилиндрической и декартовой системе координат, практически одинаковое при соизмеримом числе узлов в сетках. Это объясняется идентичностью проделываемых операций. Поэтому полное время расчёта пропорционально числу итераций.
Точность расчёта при одинаковом числе итераций различна (см. рис. 7 и 8). Практический интерес представляет область, в которой относительная погрешность не превышает нескольких процентов. В декартовой системе координат предельная минимальная погрешность для рассматриваемых сеток наблюдается при 600 итерациях. Аналогичные сетки в цилиндрической системе координат не могут обеспечить аналогичную точность даже при числе итераций, превышающем 10000.
—$— Црщшндрическая система координат —В— Декартовая система координат
Рис. 10. Зависимость относительной погрешности dU от числа итераций N для цилиндрической и декартовой системы координат
Скорость счёта составляла 95,298 итераций в секунду (1 итерация за 0,0105 с). В декартовой системе координат минимально возможная погрешность при данной дискретности сетки (0,017%) достигалась за 1минуту 45 секунд. В цилиндрической системе координат для достижения такой точности необходимо более 5,5 минуты. При дальнейшем увеличении числа итераций цилиндрическая система координат способна обеспечить значительно более высокую точность (порядка 10_5 %). Декартовая система координат позволяет значительно быстрее получить решение с погрешностью в несколько процентов, а это важно при проведении большого количества расчётов. В этой области скорость сходимости решения уравнения Пуассона в декартовой системе координат превосходит скорость сходимости в цилиндрической системе координат более чем на порядок.
Научная новизна данной работы заключается в том, что в декартовой системе координат численное решение уравнения Пуассона конечно-разностным неявным итерационным методом находится быстрее, чем в цилиндрической системе координат при соизмеримом числе узлов соответствующих сеток. Представлены расчётные зависимости, которые дают количественную оценку скорости счёта при заданной дискретности сетки в обеих системах координат.
Практическое значение полученных результатов заключается в возможности ускорения расчётов распределения потенциала, создаваемого электродами практически любой геометрии. В частности, результаты работы были использованы при моделировании электронных пучков в магнетронных пушках.
Сравнение использованного метода решения уравнения Пуассона с аналогичными методами показывает преимущество выбранного, поскольку он требует меньше оперативной памяти, которая ограничена.
Литература: 1 Поттер Д. Вычислительные методы в физике. M.: Мир, 1975. 391 с. 2. Самарский А. А. Теория разностных схем. М.: Наука, 1983. 616с. 3. Молоковский С.И., Сушков А.Д. Интенсивные электронные и ионные пучки. Ленинград: Энергия, 1972. 270с. 4. Волколу-
пов Ю.Я., Довбня А.Н., Закутин В.В., Красноголовец М.А., Решетняк Н.Г., Ромасько В.П. Быстрое формирование электронного пучка в магнетронной пушке с вторично-эмиссионным металлическим катодом // ЖТФ, 2001, Т.71, №9. C.134-136. 5. Агафонов А.В, Тараканов В.П., Федоров В.М. Динамика нарушения магнитной изоляции и самоорганизация электронного потока в магнетронном диоде // ЖТФ. 2004. Т.74, №1. C.93-103.
Поступила в редколлегию 11.03.2004
Рецензент: д-р техн. наук, проф. Стасев Ю.В.
Чурюмов Геннадий Иванович, д-р физ.-мат. наук, профессор кафедры ФОЭТ ХНУРЭ. Научные интересы: Методы математического моделирования, СВЧ электроника и электродинамика, оптоэлектроника. Адрес: Украина, 61166, Харьков, пр. Ленина, 14, тел. 70-21-057.
Старчевский Юрий Львович, аспирант кафедры ФОЭТ ХНУРЭ. Научные интересы: физика электронных пучков, программирование, математическое моделирование. Адрес: Украина, 61166, Харьков, пр. Ленина, 14, тел. 32-49-19.
Лебедев Олег Григорьевич, канд. техн. наук, доцент, начальник кафедры №304 ХИ ВВС. Научные интересы: радиолокация и навигация, аэродромное оборудование. Адрес: Украина, 61000, Харьков, ул. Клочковс-кая, 228. тел. 30-82-14.
Новиков Николай Иванович, канд. военных наук, зам. начальника факультета по учебной и научной работе ХИ ВВС. Научные интересы: радиосвязь. Адрес: Украина, 61000, Харьков, ул. Клочковская, 228.
СЛОЖНЫЕ КОЛЕБАНИЯ ПРОСТЫХ СИСТЕМ С S-ОБРАЗНОЙ ВОЛЬТАМПЕРНОЙ ХАРАКТЕРИСТИКОЙ
ЛОШИЦКИЙ П.П., НИКОЛОВ Н.А.,
АЛЬ СИНЖЛАВИ Ш.______________________
Рассматриваются преобразователи стохастичности, построенные на электронных приборах с S-образной вольтамперной характеристикой. Показывается, что для генераторов, построенных на таких элементах (ЛПД, неоновая лампа, динистор), возможна реализация перехода к хаосу по сценарию, связанному с инерционностью основных параметров активного элемента.
Явление хаотизации динамических процессов в детерминированных нелинейных системах, которое совсем недавно казалось невероятным в рамках традиционных взглядов теории колебаний, в настоящее время представляет собой не только хорошо теоретически обоснованный факт, но и получило широкое практическое применение.
Одной из областей такого применения детерминированного хаоса является создание генераторов стохастичности. Основное их отличие от обычных генераторов шума заключается в следующем. В генераторах шума имеется первичный источник
шума, случайный сигнал которого требует достаточно большого усиления, что ограничивает область его применения. В генераторах стохастичности первичный источник используется для управления регулярными колебаниями большой амплитуды, преобразуя их в стохастические. При этом генераторы стохастичности создают столь сложные динамические колебания, что они мало отличаются от шумового сигнала. Таким образом, отличия генераторов шума от генераторов стохастичности заключаются не только в величине выходной мощности сигнала, но и в механизмах его реализации [ 1]. В теории детерминированного хаоса генераторы стохастичности нестрого делят на преобразователи, усилители и генераторы стохастичности.
Для преобразователей стохастичности источниками первичной случайности могут быть микроплазмы в твердотельных приборах, флуктуации параметров в вакуумных приборах, а также различные инерционные процессы.
Флуктуации оказывают относительно слабое влияние на устойчивые системы, имеющие малые отношения рабочей поверхности к объему активно -го элемента и работающие в частотных диапазонах, далеких от частоты (времени) релаксации флуктуаций. В неустойчивых системах рабочие частоты соизмеримы с частотами релаксации флуктуаций, и развитые поверхности последних играют решаю -щую роль в работе прибора, качественно меняя его параметры.
http://zaochnik.com/spravochnik/fizika/elektricheskoe-pole/uravnenie-puassona/
http://cyberleninka.ru/article/n/sravnenie-chislennogo-resheniya-uravneniya-puassona-v-dekartovoy-i-tsilindricheskoy-sistemah-koordinat